2008年中考数学分类真理练习22与圆有关的位置关 17页

‎22与圆有关的位置关系 ‎1、两圆半径分别为3和4，圆心距为7，则这两个圆( )‎ Ａ．外切 Ｂ．相交 Ｃ．相离 Ｄ．内切 答案：1、A；‎ ‎（2008江西）6．在平面直角坐标系中，以点（2，3）为圆心，2为半径的圆必定（ ）‎ ‎ A．与轴相离、与轴相切 B．与轴、轴都相离 ‎ C．与轴相切、与轴相离 　D．与轴、轴都相切 答案：Ａ ‎（2008温州）8.已知和外切，它们的半径分别为‎2cm和‎5cm，则的长是（ ）‎ A．‎2cm B．‎3cm C．‎5cm D．‎‎7cm 答案D ‎（2008金华）12.相交两圆的半径分别为‎6cm和‎8cm，请你写出一个符合条件的圆心距为 cm.‎ 答案：答案不唯一，只要填一个大于2且小于14的实数均可 ‎（2008 嘉兴）定义1：与四边形四边都相切的圆叫做四边形的内切圆．‎ 定义2：一组邻边相等，其他两边也相等的凸四边形叫做筝形．‎ 探究：任意筝形是否一定存在内切圆？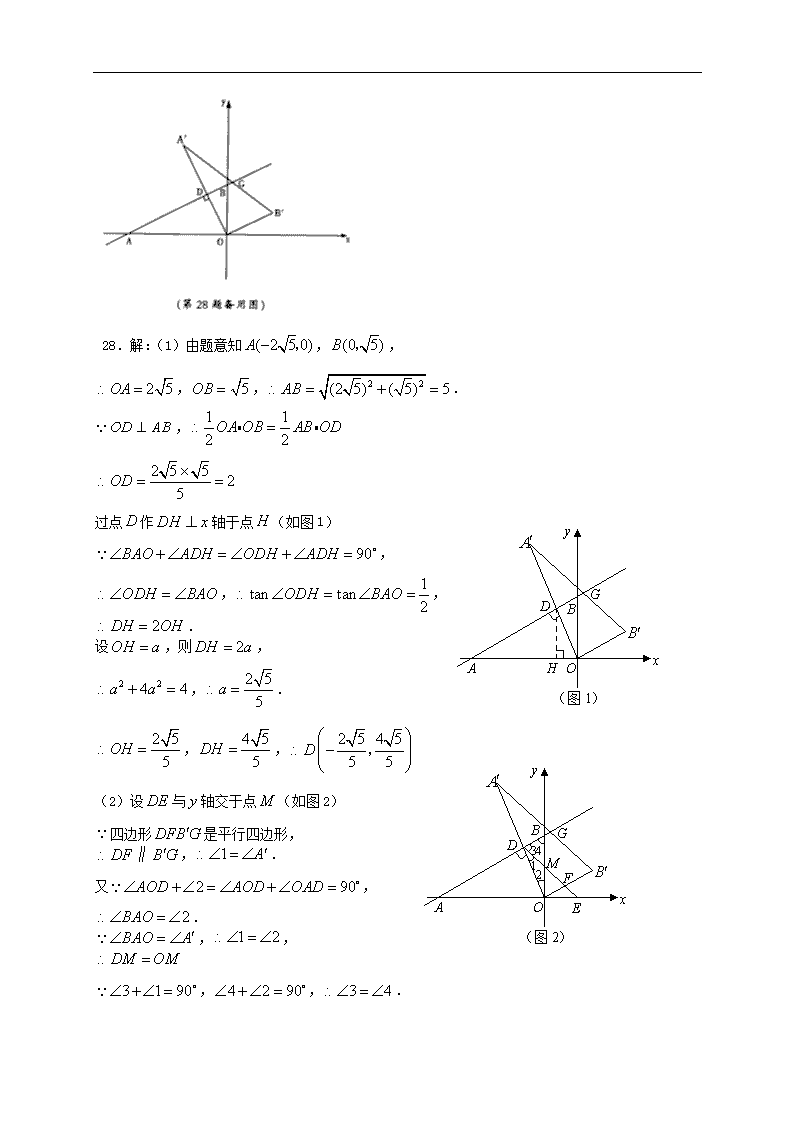‎ 答案： ．（填“是”或“否”）‎ 答案：是 ‎(2008甘肃白银)请你类比一条直线和一个圆的三种位置关系，在图11①、②、③中，分别各画出一条直线，使它与两个圆都相离、都相切、都相交，并在图11④中也画上一条直线，使它与两个圆具有不同于前面3种情况的位置关系．‎ 图11‎ 答案不唯一． 可供参考的有：‎ 相离：‎ 相切： ‎ 相交： ‎ 其它：‎ 图1‎ ‎（2008甘肃兰州）图1是北京奥运会自行车比赛项目标志，则图中 两轮所在圆的位置关系是（ D ）‎ A．内含 B．相交 C．相切 D．外离 ‎1.（2008哈尔滨市T28）如图，在平面直角坐标系中，直线y＝与x轴、y轴分别交于A、B两点，将△ABO绕原点O顺时针旋转得到△A´B´O，并使OA´⊥AB，垂足为D，直线AB与线段A´B´相交于点G．动点E从原点O出发，以1个单位/秒的速度沿x轴正方向运动，设动点E运动的时间为t秒．‎ ‎（1）求点D的坐标；‎ ‎（2）连接DE，当DE与线段OB´相交，交点为F，且四边形DFB´G是平行四边形时，（如图2）求此时线段DE所在的直线的解析式；‎ ‎（3）若以动点为E圆心，以为半径作⊙E，连接A´E，t为何值时。Tan∠EA´B´＝？并判断此时直线A´O与⊙E的位置关系，请说明理由。‎ ‎ ‎ ‎28．解：（1）由题意知，，‎ ‎，，．‎ ‎，‎ ‎ ‎ x y D A O H B G ‎（图1）‎ 过点作轴于点（如图1）‎ ‎，‎ ‎，，‎ ‎．‎ 设，则，‎ ‎，．‎ x y D A O B G ‎（图2）‎ E F M ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎，， ‎ ‎（2）设与轴交于点（如图2）‎ 四边形是平行四边形，‎ ‎，．‎ 又，‎ ‎．‎ ‎，，‎ ‎，，．‎ ‎，．‎ 点是中点，‎ 设线段所在直线解析式为．‎ 把，代入，‎ 得解得．‎ 线段所在直线的解析式为 ‎ ‎（3）设直线交轴于点（如图3），过点作轴于点．‎ ‎，，，‎ y x A K G D T O S1‎ S2‎ E1‎ E2‎ B Q1‎ N Q2‎ ‎（图3）‎ ‎，，，．‎ 过点作轴于点，‎ 同理，‎ ‎．‎ 设直线的解析式为，‎ ‎，解得．‎ 直线的解析式为 ‎ ‎，，．‎ 当点在点左侧点位置时，过点作于点．‎ ‎，设m，则m.‎ 又，m，．‎ ‎，，，此时 ‎ 过点作于点．‎ ‎，‎ ‎，．‎ 的半径为，而，‎ 与直线相交． ‎ 当点在点右侧点位置时 过点作于点 同理此时 ‎ 过点作于点 同理．‎ 的半径为，‎ 与直线相切 当或时，；‎ 当时直线与相交，当时直线与相切．‎ ‎1．（2008山东青岛）已知和的半径分别为‎3cm和‎2cm，圆心距cm，则两圆的位置关系是（ ）‎ A．相切 B．内含 C．外离 D．相交 ‎【参考答案】D ‎【解析】本题考查两圆的位置关系，两圆的位置关系取决于两圆的圆心距.设两圆半径分别为R、r，两圆的圆心距为d，则当d＞R＋r时，两圆外离；当d＝R＋r时，两圆外切；当R－r＜d＜R＋r时，两圆相交；当d＝R－r时，两圆内切；当d＜R－r时，两圆内含.‎ ‎16．(08泰州)分别以梯形的上底、下底的长为直径作、‎ ‎，若两圆的圆心距等于这个梯形的中位线长，则这两个圆的位置关系是 ．相外切（如写相切不给分）‎ A C B D ‎1、(12T)(湖北省襄樊,3分)如图6，中，，则的度数为 ．12． ‎ ‎2、（17T）（2008湖北省黄冈市，本题满分8分）如图是“明清影视城”的圆弧形门，黄红同学到影视城游玩，很想知道这扇门的相关数据．于是她从景点管理人员处打听到：这个圆弧形门所在的圆与水平地面是相切的，cm，cm，且与水平地面都是垂直的．根据以上数据，请你帮助黄红同学计算出这个圆弧形门的最高点离地面的高度是多少？‎ D E C A O B ‎3、（16T）（2008湖北省黄冈市，本题满分8分）已知：如图，在中，，以为直径的交于点，过点作于点．‎ 求证：是的切线．‎ ‎12．（2008内江市）下列命题中，真命题的个数为（ ）‎ ‎①对角线互相垂直平分且相等的四边形是正方形 ‎②如果四边形的两条对角线互相垂直，那么它的面积等于两条对角线长的积的一半 ‎③在一个圆中，如果弦相等，那么所对的圆周角相等 ‎④已知两圆半径分别为5，3，圆心距为2，那么两圆内切 A．1 B．2 C．3 D．4‎ 答案：C A C D O B 1. ‎（2008黄石）如图，为的直径，点在上，，则 ．‎ A C D O B 答案： .‎ ‎1、(24T)(湖北省襄樊,本小题满分10分）‎ 如图14，直线经过上的点，并且，，交直线于，连接．‎ ‎（1）求证：直线是的切线；‎ ‎（2）试猜想三者之间的等量关系，并加以证明；‎ ‎（3）若，的半径为3，求的长．‎ ‎24．解：（1）证明：如图3，连接．‎ ‎，，．‎ 是的切线．‎ ‎（2）．‎ 是直径，．‎ ‎．‎ 又，，‎ ‎．‎ 又，．‎ ‎．．‎ ‎（3），．‎ ‎，．‎ 设，则．‎ 又，．‎ 解之，得，．，．‎ ‎．‎ A D C B O ‎（8题图）‎ ‎8．（2008内江市）如图，在直角梯形中，，，且 ‎，是的直径，则直线与的位 置关系为（ ）‎ A．相离 B．相切 C．相交 D．无法确定 13．（08南京）已知⊙O1和⊙O2的半径分别为3cm和5cm，且它们内切，则圆心距等于 2 cm．‎ 27．（08南京）（8分）如图，已知的半径为6cm，射线经过点，，射线与相切于点．两点同时从点出发，点以5cm/s的速度沿射线方向运动，点以4cm/s的速度沿射线方向运动．设运动时间为s．‎ ‎（第27题）‎ A B Q O P N M ‎（1）求的长；‎ ‎（2）当为何值时，直线与相切？‎ ‎（1）连接．‎ 与相切于点，‎ ‎，即． 2分 ‎，，‎ ‎． 3分 ‎（2）过点作，垂足为．‎ 点的运动速度为5cm/s，点的运动速度为4cm/s，运动时间为s，‎ ‎，．‎ ‎，，‎ ‎．‎ ‎，‎ ‎．‎ ‎． 4分 ‎，‎ 四边形为矩形．‎ ‎．‎ 的半径为6，‎ 时，直线与相切．‎ ‎①当运动到如图1所示的位置．‎ 图1‎ A B Q O P N M C ‎．‎ 由，得．‎ 解得． 6分 ‎②当运动到如图2所示的位置．‎ 图2‎ A B Q O P N M C ‎．‎ 由，得．‎ 解得．‎ 所以，当为0.5s或3.5s时直线与相切． 8分 18．（08连云港）（本小题满分8分）‎ B C P O A ‎（第18题图）‎ 如图，内接于，为的直径，，，过点作的切线与的延长线交于点，求的长．‎ 解：是的直径，．又，‎ ‎，． 3分 又，所以是等边三角形，由，知． 5分 是的切线，．‎ 在中，，，‎ 所以，． 8分 ‎25．（08连云港）（本小题满分12分）‎ 我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆．例如线段的最小覆盖圆就是以线段为直径的圆．‎ A A B B C C ‎（第25题图1）‎ ‎（1）请分别作出图1中两个三角形的最小覆盖圆（要求用尺规作图，保留作图痕迹，不写作法）；‎ ‎（2）探究三角形的最小覆盖圆有何规律？请写出你所得到的结论（不要求证明）；‎ G H E F ‎（第25题图2）‎ ‎（3）某地有四个村庄（其位置如图2所示），现拟建一个电视信号中转站，为了使这四个村庄的居民都能接收到电视信号，且使中转站所需发射功率最小（距离越小，所需功率越小），此中转站应建在何处？请说明理由．‎ 解：（1）如图所示： 4分 A A B B C C ‎（第25题答图1）‎ ‎（注：正确画出1个图得2分，无作图痕迹或痕迹不正确不得分）‎ ‎（2）若三角形为锐角三角形，则其最小覆盖圆为其外接圆； 6分 若三角形为直角或钝角三角形，则其最小覆盖圆是以三角形最长边（直角或钝角所对的边）为直径的圆． 8分 G H E F ‎（第25题答图2）‎ M ‎（3）此中转站应建在的外接圆圆心处（线段的垂直平分线与线段的垂直平分线的交点处）． 10分 理由如下：‎ 由，‎ ‎，，‎ 故是锐角三角形，‎ 所以其最小覆盖圆为的外接圆，‎ 设此外接圆为，直线与交于点，‎ 则．‎ 故点在内，从而也是四边形的最小覆盖圆．‎ 所以中转站建在的外接圆圆心处，能够符合题中要求．‎ ‎ 12分 ‎[2008福建省南平市]12．如图，奥运五环标志里，包含了圆与圆的位置关系中的 外离和 ．相交 ‎[2008年福建省宁德市]6.如图，国际奥委会会旗上的图案是由五个圆环组成，在这个图案中 第6题图 反映出的两圆位置关系有（ B．‎ A.内切、相交 B.外离、相交 C.外切、外离 D.外离、内切 ‎（2008徐州）⊙O1和⊙O2的半径分别为5和2，O1O2＝3，则⊙O1和⊙O2的位置关系是 B A.内含　　　B.　内切　　　C.相交　　　D.外切 K M A P B D T C N ‎（第27题）‎ ‎（2008苏州）如图，在中，．平分交于，以为圆心，为半径作交于，的延长线交于，直线交于两点，作于．‎ ‎（1）求证：；‎ ‎（2）求证：；‎ ‎（3）当时，求证：．‎ 证明：（1）平分，，‎ ‎，又．‎ ‎（2）平分，‎ ‎．‎ 又，．‎ ‎．‎ ‎，．．‎ ‎（3）和为 的割线，．‎ ‎．‎ ‎．‎ ‎．‎ 在和中，‎ ‎．‎ ‎，即．‎ ‎．‎ ‎（2008 大连市）5．已知两圆的半径分别为6和8，圆心距为7，则两圆的位置关系是 ( )‎ A．外离 B．外切 C．相交 D．内切 答案：C ‎（2008年江苏省无锡市，27T，10分）如图，已知点从出发，以1个单位长度/秒的速度沿轴向正方向运动，以为顶点作菱形，使点在第一象限内，且；以为圆心，为半径作圆．设点运动了秒，求：‎ ‎（1）点的坐标（用含的代数式表示）；‎ ‎（2）当点在运动过程中，所有使与菱形的边所在直线相切的的值．‎ ‎27．解：（1）过作轴于，‎ ‎，，‎ ‎，，‎ 点的坐标为． （2分）‎ B A D O P C x y 图1‎ ‎（2）①当与相切时（如图1），切点为，此时，‎ y x B C P O A E 图2‎ ‎，，‎ ‎． （4分）‎ ‎②当与，即与轴相切时（如图2），则切点为，，‎ 过作于，则， （5分）‎ ‎，． （7分）‎ ‎③当与所在直线相切时（如图3），设切点为，交于，‎ 则，，‎ ‎． （8分）‎ y x A F C B P O G H 图3‎ 过作轴于，则，‎ ‎，‎ 化简，得，‎ 解得，‎ ‎，‎ ‎．‎ 所求的值是，和． （10分）‎ ‎（2008青海）27．已知，如图，直线交于两点，是直径，平分交于，过作于．‎ ‎（1）求证：是的切线；‎ 第27题图 C O B A D M E N ‎（2）若cm，cm，求的半径．‎ 答案：C O B A D M E N 27．（1）证明：连接．‎ ‎，‎ ‎． （1分）‎ ‎，‎ ‎． （2分）‎ ‎． （3分）‎ ‎，‎ ‎．‎ 即． （4分）‎ 在上，‎ 是的切线． （5分）‎ ‎（2）解：，，，‎ ‎． （6分）‎ 连接．‎ 是的直径，‎ ‎． （7分）‎ ‎，‎ ‎． （8分）‎ ‎．‎ ‎．‎ 则（cm）． （9分）‎ 的半径是‎7.5cm． （10分）‎ O2‎ O3‎ O1‎ ‎（2008赤峰）7．如图，，，两两相外切，的半径，的半径，的半径，则是（ B ）‎ A．锐角三角形 B．直角三角形 ‎ C．钝角三角形 D．锐角三角形或钝角三角形 ‎(2008宁夏)8．已知⊙O和⊙O相切，两圆的圆心距为‎9cm，⊙的半径为‎4cm，则⊙O的半径为（ ）D A．5cm B．13cm C．9 cm 或‎13cm D．5cm 或‎13cm ‎（2008赤峰）24.如图（1），两半径为的等圆和相交于两点，且过点．过点作直线垂直于，分别交和于两点，连结．‎ ‎（1）猜想点与有什么位置关系，并给出证明；‎ ‎（2）猜想的形状，并给出证明；‎ ‎（3）如图（2），若过的点所在的直线不垂直于，且点在点的两侧，那么（2）中的结论是否成立，若成立请给出证明．‎ O2‎ O1‎ N M B A 图（1）‎ O2‎ O1‎ N M B A 图（2）‎ 解：（1）在上 （1分）‎ 证明：过点，‎ ‎．‎ 又的半径也是，‎ O2‎ O1‎ N M B A 图（2）‎ 点在上． （3分）‎ ‎（2）是等边三角形 （5分）‎ 证明：，‎ ‎．‎ 是的直径，是的直径，‎ 即，在上，在上． （7分）‎ 连结，则是的中位线．‎ ‎．‎ ‎，则是等边三角形． （9分）‎ ‎（3）仍然成立． （11分）‎ 证明：由（2）得在中所对的圆周角为．‎ 在中所对的圆周角为． （12分）‎ 当点在点的两侧时，‎ 在中所对的圆周角，‎ 在中所对的圆周角，‎ 是等边三角形． （14分）‎ ‎（2），（3）是中学生猜想为等腰三角形证明正确给一半分．‎ ‎23．(2008芜湖)（本小题满分12分）‎ 在Rt△ABC中，BC=9， CA=12，∠ABC的平分线BD交AC与点D， DE⊥DB交AB于点E．‎ ‎（1）设⊙O是△BDE的外接圆，求证:AC是⊙O的切线;‎ ‎（2）设⊙O交BC于点F，连结EF，求的值．‎ ‎（1）证明：由已知DE⊥DB，⊙O是Rt△BDE的外接圆，∴BE是⊙O的直径，点O是BE的中点，连结OD，‎ ‎∵，∴．‎ 又∵BD为∠ABC的平分线，∴．‎ ‎∵，∴．‎ ‎∴，即∴‎ 又∵OD是⊙O的半径，‎ ‎∴AC是⊙O的切线． （2） 解：设⊙O的半径为r， ‎ 在Rt△ABC中， ，‎ ‎∴‎ ‎∵，，∴△ADO∽△ACB．‎ ‎∴．∴．‎ ‎∴．∴‎ 又∵BE是⊙O的直径．∴．∴△BEF∽△BAC ‎∴．‎