中考数学第一轮复习导学案视图与投影 9页

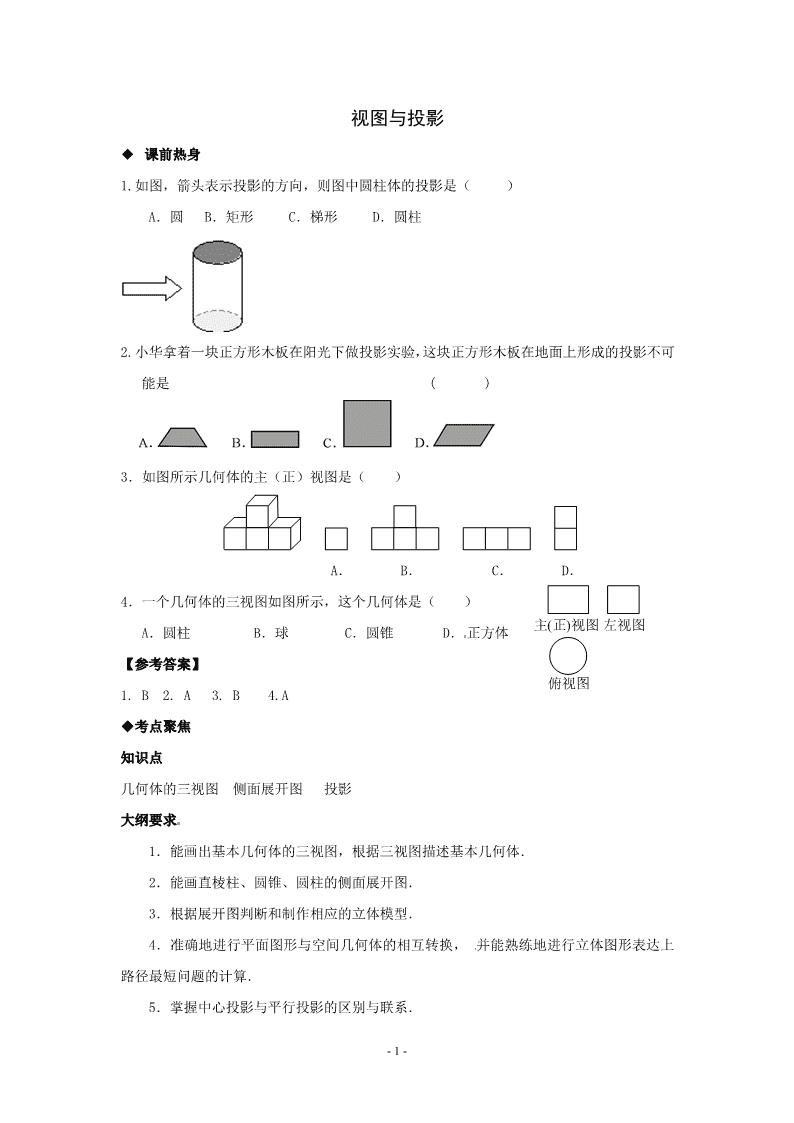
- 1 - 视图与投影 ◆ 课前热身 1.如图，箭头表示投影的方向，则图中圆柱体的投影是（ ） A．圆 B．矩形 C．梯形 D．圆柱 2.小华拿着一块正方形木板在阳光下做投影实验，这块正方形木板在地面上形成的投影不可 能是 ( ) 3．如图所示几何体的主（正）视图是（ ） A． B． C． D． 4．一个几何体的三视图如图所示，这个几何体是（ ） A．圆柱 B．球 C．圆锥 D． 正方体 【参考答案】 1. B 2. A 3. B 4.A ◆考点聚焦 知识点 几何体的三视图 侧面展开图 投影 大纲要求 1．能画出基本几何体的三视图，根据三视图描述基本几何体． 2．能画直棱柱、圆锥、圆柱的侧面展开图． 3．根据展开图判断和制作相应的立体模型． 4．准确地进行平面图形与空间几何体的相互转换，•并能熟练地进行立体图形表达上 路径最短问题的计算． 5．掌握中心投影与平行投影的区别与联系． 主(正)视图 左视图 俯视图 - 2 - 考查重点和常考题型 1.主要考查几何体的三视图，主要以选择题出现 2.主要考查根据光线的方向辨认实物的阴影。主要以选择题或者填空题出现 ◆备考兵法 1．正确区分常见几何体的三视图． 2．综合运用勾股定理，•解直角三角形的有关知识解决几何体的展开图的计算问题． 3．学习立体图形展开与将展开图折叠成立体图形的问题．•通过实际动手操作，加深理 解和掌握．培养自己的空间想象能力． ◆考点链接 1. 从 观察物体时，看到的图叫做主视图 ；从 观 察物体时，看到的图 叫做左视图 ；从 观察物体时，看到的图叫做俯视图. 2. 主视图与俯视图的 一致；主视图与左视图的 一致；俯视图与左视图的 一致. 3. 叫盲区. 4. 投影可分为平行投影与中心投影.其中 所形成的投影叫平行投影； 所形成的投影叫中心投影. 5. 利用光线是否平行或是否交于一点来判断是 投影或 投影，以及光源的位置 和物体阴影的位置. ◆ 典例精析 例 1（河南）一个几何体由一些大小相同的小正方体组成，如图是 它的主视图和俯视图，那么组成该几何体所需小正方体的个数 最少为 （ ） A．3 B．4 C．5 D．6 【解析】本题主要考查三视图的相关知识：主视图主要确定物体的长和高，左视图确定物体 的宽和高，俯视图确定物体的长和宽。由题中所给出的主视图知物体共两列，且左侧一列高 一层，右侧一列最高两层；由俯视图可知左侧一行，右侧两行，于是，可确定左侧只有一个 小正方体，而右侧可能是一行单层一行两层，出可能两行都是两层。所以图中的小正方体最 - 3 - 少 4 块，最多 5 块。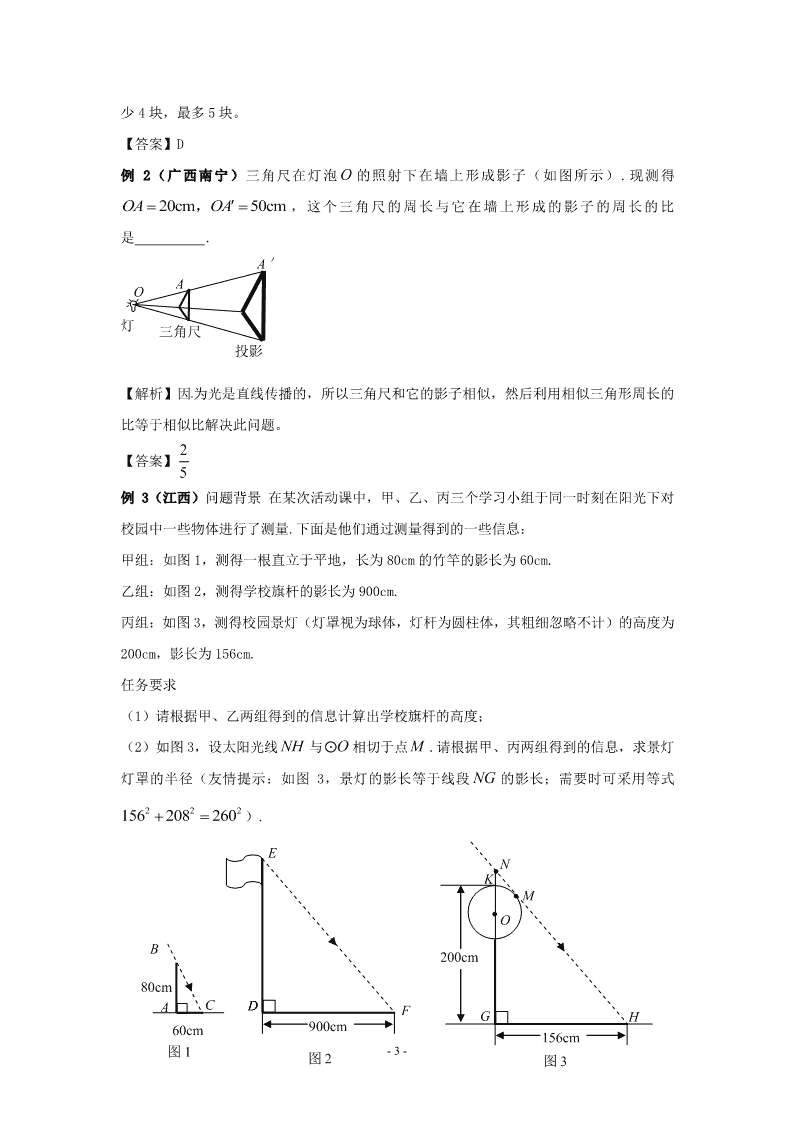 【答案】D 例 2（广西南宁）三角尺在灯泡 O 的照射下在墙上形成影子（如图所示）.现测得 20cm 50cmOA OA， ， 这 个 三 角 尺 的 周 长 与 它 在 墙 上 形 成 的 影 子 的 周 长 的 比 是 ． 【解析】因 为光是直线传播的，所以三角尺和它的影子相似，然后利用相似三角形周长的 比等于相似比解决此问题。 【答案】 2 5 例 3（江西）问题背景 在某次活动课中，甲、乙、丙三个学习小组于同一时刻在阳光下对 校园中一些物体进行了测量.下面是他们通过测量得到的一些信息： 甲组：如图 1，测得一根直立于平地，长为 80cm 的竹竿的影长为 60cm. 乙组：如图 2，测得学校旗杆的影长为 900cm. 丙组：如图 3，测得校园景灯（灯罩视为球体，灯杆为圆柱体，其粗细忽略不计）的高度为 200cm，影长为 156cm. 任务要求 （1）请根据甲、乙两组得到的信息计算出学校旗杆的高度； （2）如图 3，设太阳光线 NH 与 O 相切于点 M .请根据甲、丙两组得到的信息，求景灯 灯罩的半径（友情提示：如图 3，景灯的影长等于线段 NG 的影长；需要时可采用等式 2 2 2156 208 260）. A A′ O 灯 三角尺 投影 D D F E 900cm 图 2 B C A 60cm 80cm 图 1 G H N E 156cm M E O E 200cm 图 3 K E - 4 - 【分析】解析：利用光的直线传播可知△ABC 和△DEF 相似，从而求出旗杆的高度； 利用切线的性质，可知△KOM 和△KHG 相似，然后利用相似三角形对应边成比例的性质求出 半径 OM 的长. 【答案】解：（1）由题意可知： 90BAC EDF BCA EFD     ∠ ∠ ， ． ∴ ABC DEF△ ∽△ ． ∴ AB AC DE DF ，即 80 60 900DE  ． ∴DE=1200（cm）． 所以，学校旗杆的高度是 12m． （2）解法一： 与①类似得： AB AC GN GH ，即 80 60 156GN  ． ∴GN=208． 在 Rt NGH△ 中，根据勾股定理得： 2 2 2 2156 208 260 .NH    ∴NH=260．设 O 的半径为 rcm，连结 OM， ∵NH 切 于 M，∴OM NH ． 则 90OMN HGN   ∠ ，又 ONM HNG∠ ∠ ． ∴ OMN HGN△ ∽△ ．∴ OM ON HG HN ． 又 ( ) 8ON OK KN OK GN GK r       ． ∴ 8 156 260 rr ，解得：r=12． 所以，景灯灯罩的半径是 12cm． D D F E 900cm 图 2 B C A 60cm 80cm 图 1 图 3 G H N E 156cm M E O E 200cm K E - 5 - ◆ 迎考精炼 一、选择题 1．（广东佛山）在水平的讲台上放置圆柱形水杯和长方体形粉笔盒（右图），则它的主视 图是( ) A．图① B．图② C．图③ D．图④ 2．（黑龙江哈尔滨）右图是某一几何体的三视图，则这个几何体是（ ）． A．长方体 B．圆锥 C．圆柱 D．正三棱柱 3.（甘肃省兰州市）如图所示的几何体的俯视图是 （ ） 4.（四川省遂宁市）一个正方体的表面展开图如图所示，每个面内都标注了字母，如果从 正方体的右面看是面 D，面 C 在后面，则正方体的上面是 A.面 E B.面 F C.面 A D.面 B 5.（广西崇左）如图，下列选项中不是．．正六棱柱三视图的是（ ） A． B． C． D． 6.（甘肃庆阳）如图，晚上小亮在路灯下散步，在小亮由 A 处径直走到 B 处这一过程中，他 在地上的影子（ ） A．逐渐变短 B．先变短后变长 C．先变长后变短 D．逐渐变长 实物图 图④ 图③ 图② 图① 主视图 左视图 俯视图 A. B． C D． a a a - 6 - 7.（新疆省）如图，是由一些相同的小正方体搭成的几何体的三视图，搭成这个几何体的 小正方体个数是（ ） A．2 个 B．3 个 C．4 个 D．6 个 8.（ 山 东 省 枣 庄 市 ）如图，骰子是一个质量均匀的小正方体，它的六个面上分别刻有 1~6 个点．小明仔细观察骰子，发现任意相对两面的点数和都相等．这枚 骰子向上的一面的点数是 5，它的对面的点数是（ ） A．1 B．2 C．3 D．6 二、填空题 1.（广东省广州市）如图是由一些相同长方体的积木块搭成的几何体的三视图，则此几何体 共由________块长方体的积木搭成 2.（广西省钦州市）如图中物体的一个视图（a）的名称为_ _． 从正面看 （a） 3.（浙江省嘉兴市）一个几何体的三视图如图所示 （其中标注的 a b c， ， 为相应的边长），则这个几何体的体 积是 ． 4.（年浙江衢州）陈老师要为他家的长方形餐厅(如图)选择一张餐桌，并且想按如下要求 摆放：餐桌一侧靠墙，靠墙对面的桌边留出宽度不小于 80cm 的通道，另两边各留出宽度不 主视图 左视图 主视图 a b c b - 7 - 小于 60cm 的 通 道 ． 那么 在 下 面 四 张 餐 桌中，其大小规格符合要求的餐桌编号是 (把符合要求的编号都写上)． 三、解答题 1. （山东济宁）坐落在山东省汶 上县宝相寺内的太子灵踪塔始建于北宋（公元 1112 年），为砖彻八角形十三层楼阁式建筑.数学活动小组开展课外实践活动，在一个阳光 明媚的上午，他们去测量太子灵踪塔的高度，携带的测量工具有：测角仪、皮尺、小 镜子. （1）小华利用测角仪和皮尺测量塔高. 图 1 为小华测量塔高的示意图.她先在塔前的平地 上选择一点 A ，用测角仪测出看塔顶 ()M 的仰角 35  ，在 A 点和塔之间选择一点 B ， 测出看塔顶 的仰角 45  ，然后用皮尺量出 A 、B 两点的距离为18.6m,自身的高度 为1.6m.请你利用上述数据帮助小华计算出塔的高度（ tan35 0.7 ，结果保留整数）. （2）如果你是活动小组的一员，正准备测量塔高，而此时塔影 NP 的长为 a m（如图 2）, 你能否利用这一数据设计一个测量方案？如果能，请回答下列问题： ①在你设计的测量方案中，选用的测量工具是: ； ②要计算出塔的高，你还需要测量哪些数据？ . 230cm 餐 厅 180cm 门 桌面是边 长为 80cm 的正方形 ① 桌面是长、宽分 别为 100cm 和 64cm 的长方形 ② 桌面是半径 为45cm的圆 ③ 桌面的中间是边长 为 60cm 的正方形， 两头均为半圆 ④ A B C D M N   图 1 图 2 P - 8 - 2.（浙江省杭州市）如图是一个几何体的三视图． （1）写出这个几何体的名称； （2）根据所示数据计算这个几何体的表面积； （3）如果一只蚂蚁要从这个几何体中的点 B 出发，沿 表面爬到 AC 的中点 D，请你求出这个线路的最短路程． 3.（甘肃庆阳）一位美术老师在课堂上进行立体模型素描教学时，把由圆锥与圆柱组成的几 何体（如图所示，圆锥在圆柱上底面正中间放置）摆在讲桌上，请你在指定的方框内分别画 出这个几何体的三视图（从正面、左面、上面看得到的视图）． 第 3 题 主视图 左视图 俯视图 俯视图 A B C D 主视图 4 6 左视图 单位：厘米 - 9 - 【参考答案】 一、选择题 1.B 2.A 3.C 4.A 5.A 6.B 7.C 8.B 二、填空题 1.4 2.主视图 3. abc 4.①②③④ 三、解答题 1.解:（1）设CD 的延长线交 MN 于 E 点， 长为 xm ，则 ( 1.6)ME x m . ∵ 045  ,∴ 1.6DE ME x   .∴ 1.6 18.6 17CE x x     . ∵ 0tan tan35ME CE  ,∴ 1.6 0.717 x x   ,解得 45xm . ∴太子灵踪塔 ()MN 的高度为 45m . (2) ①测角仪、皮尺； ② 站在 P 点看塔顶的仰角、自身的高度. (注：答案不唯一) 2.（1）圆锥； （2）表面积 S=  164122  rrlSS 圆扇形 （平方厘米） （3） 如图将圆锥侧面展开，线段 BD 为所求的最短路程 . 由条件得，∠BAB′=120°，C 为弧 BB′中点，所以 BD= 33 . 3.