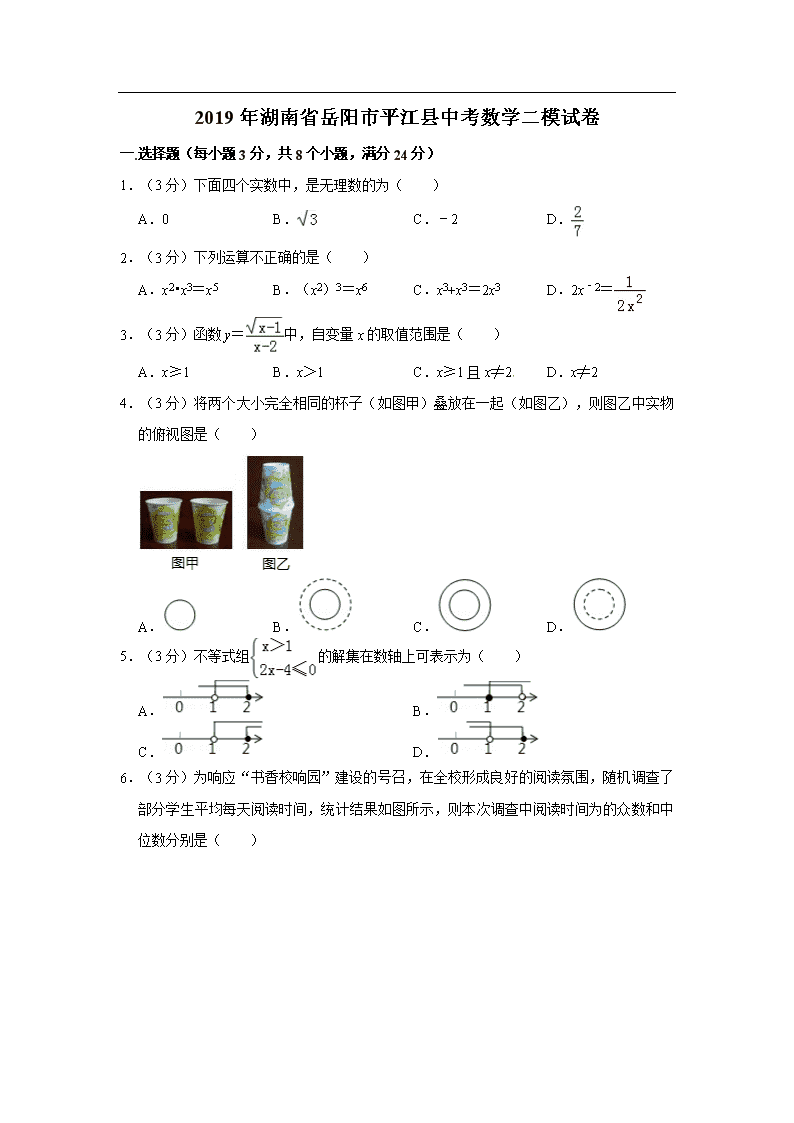
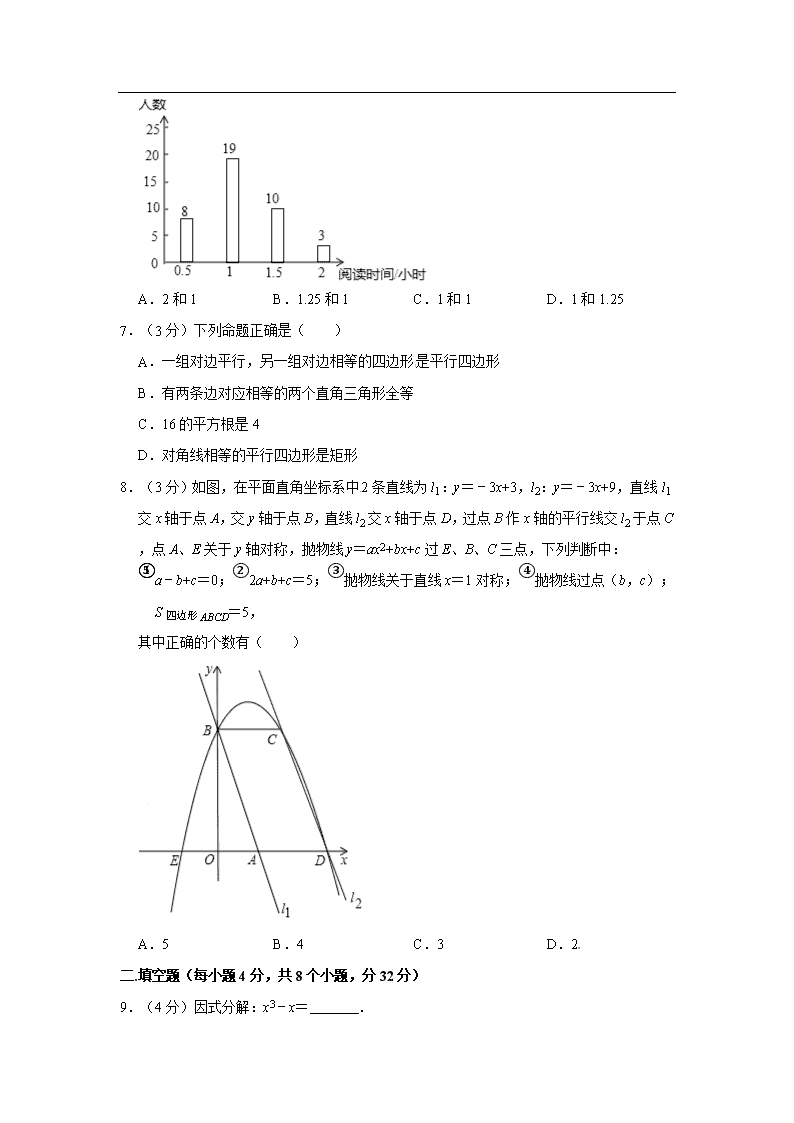
- 937.50 KB
- 2021-11-12 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2019年湖南省岳阳市平江县中考数学二模试卷
一.选择题(每小题3分,共8个小题,满分24分)
1.(3分)下面四个实数中,是无理数的为( )
A.0 B. C.﹣2 D.
2.(3分)下列运算不正确的是( )
A.x2•x3=x5 B.(x2)3=x6 C.x3+x3=2x3 D.2x﹣2=
3.(3分)函数y=中,自变量x的取值范围是( )
A.x≥1 B.x>1 C.x≥1且x≠2 D.x≠2
4.(3分)将两个大小完全相同的杯子(如图甲)叠放在一起(如图乙),则图乙中实物的俯视图是( )
A. B. C. D.
5.(3分)不等式组的解集在数轴上可表示为( )
A. B.
C. D.
6.(3分)为响应“书香校响园”建设的号召,在全校形成良好的阅读氛围,随机调查了部分学生平均每天阅读时间,统计结果如图所示,则本次调查中阅读时间为的众数和中位数分别是( )
[来源:学科网ZXXK]
A.2和1 B.1.25和1 C.1和1 D.1和1.25
7.(3分)下列命题正确是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.有两条边对应相等的两个直角三角形全等
C.16的平方根是4
D.对角线相等的平行四边形是矩形
8.(3分)如图,在平面直角坐标系中2条直线为l1:y=﹣3x+3,l2:y=﹣3x+9,直线l1交x轴于点A,交y轴于点B,直线l2交x轴于点D,过点B作x轴的平行线交l2于点C,点A、E关于y轴对称,抛物线y=ax2+bx+c过E、B、C三点,下列判断中:
①a﹣b+c=0;②2a+b+c=5;③抛物线关于直线x=1对称;④抛物线过点(b,c);⑤S四边形ABCD=5,
其中正确的个数有( )
A.5 B.4 C.3 D.2
二.填空题(每小题4分,共8个小题,分32分)
9.(4分)因式分解:x3﹣x= .
10.(4分)据最新统计,苏州市常住人口约为1062万人.数据10 620 000用科学记数法可表示为 .
11.(4分)在等腰△ABC中,∠A、∠B、∠C的对边分别为a、b,c,已知a=3,b和c是关于x的方程x2+mx+2﹣m=0的两个实数根,则△ABC的周长是 .
12.(4分)分式方程=的解是 .
13.(4分)点P的坐标是(a,b),从﹣2,﹣1,0,1,2这五个数中任取一个数作为a的值,再从余下的四个数中任取一个数作为b的值,则点P(a,b)在平面直角坐标系中第二象限内的概率是 .
14.(4分)如图,把一张长方形的纸条ABCD沿EF折叠,若∠BFC′比∠BFE多6°,则∠EFC= .
[来源:学科网]
15.(4分)如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120m,DC=60m,EC=50m,求得河宽AB= m.
16.(4分)如图,在半⊙O中,AB是直径,点D是⊙O上一点,点C是的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④AC2=CQ•CB,其中结论正确的是 .
三.解答题(满分64分)
17.(6分)计算:(﹣1)2019﹣+(π﹣3)0+4cos45°
18.(6分)如图,矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD.求证:四边形AODE是菱形.
19.(8分)已知反比例函数的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2).
(1)求这两个函数的解析式;
(2)如果点C与点A关于y轴对称,求△ABC的面积.
20.(8分)学习习近平总书记关于生态文明建设重要讲话,牢固树立“绿水青山就是金山银山”的科学观,让环保理念深入到学校,某校张老师为了了解本班学生3月植树成活情况,对本班全体学生进行了调查,并将调查结果分为了三类:A:好,B:中,C:差.
请根据图中信息,解答下列问题:
(1)求全班学生总人数;
(2)将上面的条形统计图与扇形统计图补充完整;
(3)张老师在班上随机抽取了4名学生,其中A类1人,B类2人,C类1人,若再从这4人中随机抽取2人,请用画树状图或列表法求出全是B类学生的概率.
21.(8分)多好佳水果店在批发市场购买某种水果销售,第一次用1500元购进若干千克,并以每千克9元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1694元所购买的水果比第一次多20千克,以每千克10元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价45%售完剩余的水果.
(1)求第一次水果的进价是每千克多少元.
(2)该水果店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
22.(8分)近年来,共享单车服务的推出(如图1),极大的方便了城市公民绿色出行,图2是某品牌某型号单车的车架新投放时的示意图(车轮半径约为30cm),其中BC∥直线l,∠BCE=71°,CE=54cm.[来源:学|科|网Z|X|X|K]
(1)求单车车座E到地面的高度;(结果精确到1cm)
(2)根据经验,当车座E到CB的距离调整至等于人体胯高(腿长)的0.85时,坐骑比较舒适.小明的胯高为70cm,现将车座E调整至座椅舒适高度位置E′,求EE′的长.(结果精确到0.1cm)
(参考数据:sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)
23.(10分)在Rt△ABC中,∠ACB=90°,点D与点B在AC同侧,∠DAC>∠BAC,且DA=DC,过点B作BE∥DA交DC于点E,M为AB的中点,连接MD,ME.
(1)如图1,当∠ADC=90°时,线段MD与ME的数量关系是 ;
(2)如图2,当∠ADC=60°时,试探究线段MD与ME的数量关系,并证明你的结论;
(3)如图3,当∠ADC=α时,求的值.
24.(10分)如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
[来源:学&科&网Z&X&X&K]
2019年湖南省岳阳市平江县中考数学二模试卷
参考答案与试题解析
一.选择题(每小题3分,共8个小题,满分24分)
1.(3分)下面四个实数中,是无理数的为( )
A.0 B. C.﹣2 D.
【分析】根据无理数的定义:无限不循环小数是无理数即可求解.
【解答】解:A、0是有理数,故选项错误;
B、是无理数,故选项正确;
C、﹣2是有理数,故选项错误;
D、是有理数,故选项错误.
故选:B.
2.(3分)下列运算不正确的是( )
A.x2•x3=x5 B.(x2)3=x6 C.x3+x3=2x3 D.2x﹣2=
【分析】根据同底数幂的运算法则及合并同类项的法则进行计算即可.
【解答】解:A、x2•x3=x5,正确;
B、(x2)3=x6,正确;
C、x3+x3=2x3,正确;
D、,错误;
故选:D.
3.(3分)函数y=中,自变量x的取值范围是( )
A.x≥1 B.x>1 C.x≥1且x≠2 D.x≠2
【分析】根据分式的分母不为零、被开方数是非负数来求x的取值范围.
【解答】解:依题意得:x﹣1≥0且x﹣2≠0,
解得x≥1且x≠2.
故选:C.
4.(3分)将两个大小完全相同的杯子(如图甲)叠放在一起(如图乙),则图乙中实物的俯视图是( )
A. B. C. D.
【分析】俯视图是从上面看,可以看到上面杯子的底,是圆形,可以看到两杯子的口,也是圆形.
【解答】解:从上面看,看到两个圆形,
故选:C.
5.(3分)不等式组的解集在数轴上可表示为( )
A. B.
C. D.
【分析】先求出每个不等式的解集,再求出不等式组的解集即可.
【解答】解:
∵不等式①得:x>1,
解不等式②得:x≤2,
∴不等式组的解集为1<x≤2,
在数轴上表示为:,
故选:A.
6.(3分)为响应“书香校响园”建设的号召,在全校形成良好的阅读氛围,随机调查了部分学生平均每天阅读时间,统计结果如图所示,则本次调查中阅读时间为的众数和中位数分别是( )
A.2和1 B.1.25和1 C.1和1 D.1和1.25
【分析】由统计图可知阅读时间为1小时的有19人,人数最多,所以众数为1小时;总人数为40,得到中位数应为第20与第21个的平均数,而第20个数和第21个数都是1(小时),即可确定出中位数为1小时.
【解答】解:由统计图可知众数为1小时;
共有:8+19+10+3=40人,中位数应为第20与第21个的平均数,
而第20个数和第21个数都是1(小时),则中位数是1小时.
故选:C.
7.(3分)下列命题正确是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.有两条边对应相等的两个直角三角形全等
C.16的平方根是4
D.对角线相等的平行四边形是矩形
【分析】利用平行四边形的判定,全等三角形的判定、平方根的定义及正方形的判定分别判断后即可确定正确的选项.
【解答】解:A、一组对边平行,另一组对边等的四边形可能是等腰梯形,故原命题错误;
B、有两条边对应相等的两个直角三角形全等,故原命题正确;
C、16的平方根是±4,故原命题错误;
D、对角线相等的平行四边形是矩形,正确,
故选:B.
8.(3分)如图,在平面直角坐标系中2条直线为l1:y=﹣3x+3,l2:y=﹣3x+9,直线l1交x轴于点A,交y轴于点B,直线l2交x轴于点D,过点B作x轴的平行线交l2于点C
,点A、E关于y轴对称,抛物线y=ax2+bx+c过E、B、C三点,下列判断中:
①a﹣b+c=0;②2a+b+c=5;③抛物线关于直线x=1对称;④抛物线过点(b,c);⑤S四边形ABCD=5,
其中正确的个数有( )
A.5 B.4 C.3 D.2
【分析】根据直线l1的解析式求出A(1,0),B(0,3),根据关于y轴对称的两点坐标特征求出E(﹣1,0).根据平行于x轴的直线上任意两点纵坐标相同得出C点纵坐标与B点纵坐标相同都是3,再根据二次函数图象上点的坐标特征求出C(2,3).利用待定系数法求出抛物线的解析式为y=﹣x2+2x+3,进而判断各选项即可.
【解答】解:∵直线l1:y=﹣3x+3交x轴于点A,交y轴于点B,
∴A(1,0),B(0,3),
∵点A、E关于y轴对称,
∴E(﹣1,0).
∵直线l2:y=﹣3x+9交x轴于点D,过点B作x轴的平行线交l2于点C,
∴D(3,0),C点纵坐标与B点纵坐标相同都是3,
把y=3代入y=﹣3x+9,得3=﹣3x+9,解得x=2,
∴C(2,3).
∵抛物线y=ax2+bx+c过E、B、C三点,
∴,解得,
∴y=﹣x2+2x+3.
①∵抛物线y=ax2+bx+c过E(﹣1,0),
∴a﹣b+c=0,故①正确;
②∵a=﹣1,b=2,c=3,
∴2a+b+c=﹣2+2+3=3≠5,故②错误;
③∵抛物线过B(0,3),C(2,3)两点,
∴对称轴是直线x=1,
∴抛物线关于直线x=1对称,故③正确;
④∵b=2,c=3,抛物线过C(2,3)点,
∴抛物线过点(b,c),故④正确;
⑤∵直线l1∥l2,即AB∥CD,又BC∥AD,
∴四边形ABCD是平行四边形,
∴S四边形ABCD=BC•OB=2×3=6≠5,故⑤错误.
综上可知,正确的结论有3个.
故选:C.
二.填空题(每小题4分,共8个小题,分32分)
9.(4分)因式分解:x3﹣x= x(x+1)(x﹣1) .
【分析】原式提取x,再利用平方差公式分解即可.
【解答】解:原式=x(x2﹣1)=x(x+1)(x﹣1),
故答案为:x(x+1)(x﹣1)
10.(4分)据最新统计,苏州市常住人口约为1062万人.数据10 620 000用科学记数法可表示为 1.062×107 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:数据10 620 000用科学记数法可表示为1.062×107,
故答案为:1.062×107.
11.(4分)在等腰△ABC中,∠A、∠B、∠C的对边分别为a、b,c,已知a=3,b和c是关于x的方程x2+mx+2﹣m=0的两个实数根,则△ABC的周长是 7或 .
【分析】当b=c时,利用判别式的意义得到△=m2﹣4×(2﹣m)=0,解得m=﹣
4或m=2,利用根与系数的关系m=2舍去,b+c=4,然后计算此时△ABC的周长;当b=a=3,把x=3代入方程解得m=﹣,方程变形为x2﹣x+=0,利用根与系数的关系得到3c=,解得c=,从而得到此时△ABC的周长;当c=a=3,同样方法可得△ABC的周长.
【解答】解:当b=c时,关于x的方程x2+mx+2﹣m=0的两个相等的实数根,则△=m2﹣4×(2﹣m)=0,解得m=﹣4或m=2(舍去),
当m=﹣4时,方程变形为x2﹣4m+4=0,此时b+c=4,
所以此时△ABC的周长为3+4=7;
当b=a=3,把x=3代入方程得9+3m+2﹣m=0,解得m=﹣,方程变形为x2﹣x+=0,则3c=,解得c=,
所以此时△ABC的周长为3++3=;
当c=a=3,同理可得△ABC的周长为;
综上所述,△ABC的周长为7或.
故答案为7或.
12.(4分)分式方程=的解是 x=9 .
【分析】观察可得最简公分母是x(x﹣3),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
【解答】解:方程的两边同乘x(x﹣3),得
3x﹣9=2x,
解得x=9.
检验:把x=9代入x(x﹣3)=54≠0.
∴原方程的解为:x=9.
故答案为:x=9.
13.(4分)点P的坐标是(a,b),从﹣2,﹣1,0,1,2这五个数中任取一个数作为a的值,再从余下的四个数中任取一个数作为b的值,则点P(a,b
)在平面直角坐标系中第二象限内的概率是 .
【分析】先画树状图展示所有20种等可能的结果数,再根据第二象限点的坐标特征找出点P(a,b)在平面直角坐标系中第二象限内的结果数,然后根据概率公式求解.
【解答】解:画树状图为:
共有20种等可能的结果数,其中点P(a,b)在平面直角坐标系中第二象限内的结果数为4,
所以点P(a,b)在平面直角坐标系中第二象限内的概率==.
故答案为.
14.(4分)如图,把一张长方形的纸条ABCD沿EF折叠,若∠BFC′比∠BFE多6°,则∠EFC= 122° .
【分析】本题根据平行线的性质和翻折的性质,求解即可.
【解答】解:设∠EFC=x,∠1=y,则∠BFC′=x﹣y,
∵∠BFC′比∠BFE多6°,
∴x﹣2y=6,
∵x+y=180°,
可得x=122°
故答案为122°.
15.(4分)如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120m,DC=60m,EC=50m,求得河宽AB= 100 m.
【分析】由两角对应相等可得△BAD∽△CED,利用对应边成比例可得两岸间的大致距离AB.
【解答】解:∵∠ADB=∠EDC,∠ABC=∠ECD=90°,
∴△ABD∽△ECD,
∴,,
解得:AB=(米).
故答案为:100.
16.(4分)如图,在半⊙O中,AB是直径,点D是⊙O上一点,点C是的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④AC2=CQ•CB,其中结论正确的是 ②③④ .
【分析】连接BD,由GD为圆O的切线,根据弦切角等于夹弧所对的圆周角得到∠GDP=∠ABD,再由AB为圆的直径,根据直径所对的圆周角为直角得到∠ACB为直角,由CE垂直于AB,得到∠AFP为直角,再由一对公共角,得到三角形APF与三角形ABD相似,根据相似三角形的对应角相等可得出∠APF等于∠ABD,根据等量代换及对顶角相等可得出∠GPD=∠GDP,利用等角对等边可得出GP=GD,选项②正确;由直径AB垂直于弦CE,利用垂径定理得到A为弧CE的中点,得到两条弧相等,再由C为弧AD的中点,得到两条弧相等,等量代换得到三条弧相等,根据等弧所对的圆周角相等可得出∠CAP=∠ACP,利用等角对等边可得出AP=CP,又AB为直径得到∠ACQ
为直角,利用等角的余角相等可得出∠PCQ=∠PQC,得出CP=PQ,即P为直角三角形ACQ斜边上的中点,即为直角三角形ACQ的外心,选项③正确;利用等弧所对的圆周角相等得到一对角相等,再由一对公共角相等,得到三角形ACQ与三角形ABC相似,根据相似得比例得到AC2=CQ•CB,[来源:Z+xx+k.Com]
【解答】解:∵在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,
∴弧AC=弧AD≠弧BD,
∴∠BAD≠∠ABC,选项①错误;
连接BD,如图所示:
∵GD为圆O的切线,
∴∠GDP=∠ABD,
又AB为圆O的直径,∴∠ADB=90°,
∵CE⊥AB,∴∠AFP=90°,
∴∠ADB=∠AFP,又∠PAF=∠BAD,
∴△APF∽△ABD,
∴∠ABD=∠APF,又∠APF=∠GPD,
∴∠GDP=∠GPD,
∴GP=GD,选项②正确;
∵直径AB⊥CE,
∴A为弧CE的中点,即弧AE=弧AC,
又C为弧AD的中点,
∴弧AC=弧CD,
∴弧AE=弧CD,
∴∠CAP=∠ACP,
∴AP=CP,
又AB为圆O的直径,∴∠ACQ=90°,
∴∠PCQ=∠PQC,
∴PC=PQ,
∴AP=PQ,即P为Rt△ACQ斜边AQ的中点,
∴P为Rt△ACQ的外心,选项③正确;
连接CD,如图所示:
∵弧AC=弧CD,
∴∠B=∠CAD,
又∵∠ACQ=∠BCA,
∴△ACQ∽△BCA,
∴=,即AC2=CQ•CB,选项④正确,
综上可知则正确的选项序号有②③④,
故答案为:②③④.
三.解答题(满分64分)
17.(6分)计算:(﹣1)2019﹣+(π﹣3)0+4cos45°
【分析】本题涉及零指数幂、负指数幂、二次根式化简、特殊角的三角函数值4个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
【解答】解:原式=1﹣2+1+4×,
=1﹣2+1+2,
=2.
18.(6分)如图,矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD.求证:四边形AODE是菱形.
【分析】在矩形ABCD中,可得OD=OC,由DE∥CA,AE∥BD,所以四边形AODE是平行四边形,两个条件合在一起,可得出其为菱形
【解答】证明:∵DE∥CA,AE∥BD
即 DE∥OA,AE∥OD,
∴四边形OAED是平行四边形,
在矩形ABCD中,
∴AC=BD,
∴OA=OD,
∴四边形OAED是菱形.
19.(8分)已知反比例函数的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2).
(1)求这两个函数的解析式;
(2)如果点C与点A关于y轴对称,求△ABC的面积.
【分析】(1)先把点A(1,4)代入可计算出k=4,从而得到反比例函数解析式为y1=,再利用反比例函数解析式确定B点坐标,然后利用待定系数法求一次函数解析式;
(2)先根据y轴对称的坐标特征确定C点坐标,然后根据三角形面积公式求解.
【解答】解:(1)∵点A(1,4)在的图象上,
∴k=1×4=4,
∴反比例函数解析式为y1=,
∵点B(m,2)在y1=的图象上,
∴2m=4,解得m=﹣2,
∴点B的坐标为(﹣2,﹣2),
又∵点A,B在一次函数y2=ax+b的图象上,
∴,解得,
∴一次函数解析式为y2=2x+2;
∴这两个函数的解析式分别为,y2=2x+2.
(2)∵点C与点A关于y轴对称,
∴C点坐标为(﹣1,4).
∴S△ABC=×2×6=6.
20.(8分)学习习近平总书记关于生态文明建设重要讲话,牢固树立“绿水青山就是金山银山”的科学观,让环保理念深入到学校,某校张老师为了了解本班学生3月植树成活情况,对本班全体学生进行了调查,并将调查结果分为了三类:A:好,B:中,C:差.
请根据图中信息,解答下列问题:
(1)求全班学生总人数;
(2)将上面的条形统计图与扇形统计图补充完整;
(3)张老师在班上随机抽取了4名学生,其中A类1人,B类2人,C类1人,若再从这4人中随机抽取2人,请用画树状图或列表法求出全是B类学生的概率.
【分析】(1)由A类人数及其所占百分比可得总人数;
(2)总人数减去A、B的人数求得C类人数,再分别用B、C的人数除以总人数可得对应百分比,据此即可补全图形;
(3)列表得出所有等可能结果,再根据概率公式求解可得.
【解答】解:(1)全班学生总人数为10÷25%=40(人);
(2)∵C类人数为40﹣(10+24)=6,
∴C类所占百分比为×100%=15%,B类百分比为×100%=60%,
补全图形如下:
(3)列表如下:
A
B
B
C
A
BA
BA
CA
B
AB
BB
CB
B
AB
BB
[来源:学&科&网]
CB
C
AC
BC
BC
由表可知,共有12种等可能结果,其中全是B类的有2种情况,
所以全是B类学生的概率为=.
21.(8分)多好佳水果店在批发市场购买某种水果销售,第一次用1500元购进若干千克,并以每千克9元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1694元所购买的水果比第一次多20千克,以每千克10元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价45%售完剩余的水果.
(1)求第一次水果的进价是每千克多少元.
(2)该水果店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
【分析】(1)设第一次水果的进价是每千克x元,则第二次水果的进价是每千克1.1x元,根据数量=总价÷单价结合第二次比第一次多购进20千克,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)利用数量=总价÷单价可求出第一次购进水果数量,由总利润=每千克利润×销售数量可求出第一次购进水果的销售利润,同理可求出第二次购进水果的销售利润,将二者相加即可得出结论.
【解答】解:(1)设第一次水果的进价是每千克x元,则第二次水果的进价是每千克1.1x元,
根据题意,得:﹣=20,
解得:x=2,
经检验,x=2是原方程的解,且符合题意.
答:第一次水果的进价是每千克2元.
(2)第一次购买水果1500÷2=750(千克),
第一次利润为750×(9﹣2)=5250(元).
第二次购买水果750+20=770(千克),
第二次利润为100×(10﹣2.2)+(770﹣100)×(10×55%﹣2.2)=2991(元).
5250+2991=8241(元).
答:该水果店在这两次销售中,总体上是盈利了,盈利了8241元.
22.(8分)近年来,共享单车服务的推出(如图1),极大的方便了城市公民绿色出行,图2是某品牌某型号单车的车架新投放时的示意图(车轮半径约为30cm),其中BC∥直线l,∠BCE=71°,CE=54cm.
(1)求单车车座E到地面的高度;(结果精确到1cm)
(2)根据经验,当车座E到CB
的距离调整至等于人体胯高(腿长)的0.85时,坐骑比较舒适.小明的胯高为70cm,现将车座E调整至座椅舒适高度位置E′,求EE′的长.(结果精确到0.1cm)
(参考数据:sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)
【分析】(1)作EM⊥BC于点M,由EB=ECsin∠BCE=54sin71可得答案;
(2)作E′H⊥BC于点H,先根据E′C=求得E′C的长度,再根据EE′=CE′﹣CE可得答案.
【解答】解:(1)如图1,过点E作EM⊥BC于点M,
由题意知∠BCE=71°、EC=54,
∴EB=ECsin∠BCE=54sin71°≈51.3,
则单车车座E到地面的高度为51.3+30≈81cm;
(2)如图2所示,过点E′作E′H⊥BC于点H,
由题意知E′H=70×0.85=59.5,
则E′C==≈62.6,
∴EE′=CE′﹣CE=62.6﹣54=8.6(cm).
23.(10分)在Rt△ABC中,∠ACB=90°,点D与点B在AC同侧,∠DAC>∠BAC,且DA=DC,过点B作BE∥DA交DC于点E,M为AB的中点,连接MD,ME.
(1)如图1,当∠ADC=90°时,线段MD与ME的数量关系是 MD=ME ;
(2)如图2,当∠ADC=60°时,试探究线段MD与ME的数量关系,并证明你的结论;
(3)如图3,当∠ADC=α时,求的值.
【分析】(1)先判断出△AMF≌△BME,得出AF=BE,MF=ME,进而判断出∠EBC=∠BED﹣∠ECB=45°=∠ECB,得出CE=BE,即可得出结论;
(2)同(1)的方法即可;
(3)同(1)的方法判断出AF=BE,MF=ME,再判断出∠ECB=∠EBC,得出CE=BE即可得出∠MDE=,即可得出结论.[来源:Z。xx。k.Com]
【解答】解:(1)如图1,延长EM交AD于F,
∵BE∥DA,
∴∠FAM=∠EBM,[来源:Z。xx。k.Com]
∵AM=BM,∠AMF=∠BME,
∴△AMF≌△BME,
∴AF=BE,MF=ME,[来源:学*科*网Z*X*X*K]
∵DA=DC,∠ADC=90°,
∴∠BED=∠ADC=90°,∠ACD=45°,
∵∠ACB=90°,
∴∠ECB=45°,
∴∠EBC=∠BED﹣∠ECB=45°=∠ECB,
∴CE=BE,
∴AF=CE,
∵DA=DC,
∴DF=DE,
∴DM⊥EF,DM平分∠ADC,
∴∠MDE=45°,
∴MD=ME,
故答案为MD=ME;
(2)MD=ME,理由:
如图1,延长EM交AD于F,
∵BE∥DA,
∴∠FAM=∠EBM,
∵AM=BM,∠AMF=∠BME,
∴△AMF≌△BME,
∴AF=BE,MF=ME,
∵DA=DC,∠ADC=60°,
∴∠BED=∠ADC=60°,∠ACD=60°,
∵∠ACB=90°,
∴∠ECB=30°,
∴∠EBC=∠BED﹣∠ECB=30°=∠ECB,
∴CE=BE,
∴AF=CE,
∵DA=DC,
∴DF=DE,
∴DM⊥EF,DM平分∠ADC,
∴∠MDE=30°,
在Rt△MDE中,tan∠MDE=,
∴MD=ME.
(3)如图3,延长EM交AD于F,
∵BE∥DA,
∴∠FAM=∠EBM,
∵AM=BM,∠AMF=∠BME,
∴△AMF≌△BME,
∴AF=BE,MF=ME,
延长BE交AC于点N,
∴∠BNC=∠DAC,
∵DA=DC,
∴∠DCA=∠DAC,
∴∠BNC=∠DCA,
∵∠ACB=90°,
∴∠ECB=∠EBC,
∴CE=BE,
∴AF=CE,
∴DF=DE,
∴DM⊥EF,DM平分∠ADC,
∵∠ADC=α,
∴∠MDE=,
在Rt△MDE中,=tan∠MDE=tan.
[来源:学科网]
24.(10分)如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
【分析】(1)将已知点的坐标代入已知的抛物线的解析式,利用待定系数法确定抛物线的解析式即可;
(2)①首先求得抛物线与x轴的交点坐标,然后根据已知条件得到PE=OA,从而得到方程求得x的值即可求得点P的坐标;
②用分割法将四边形的面积S四边形BCPA=S△OBC+S△OAC,得到二次函数,求得最值即可.
【解答】解:(1)∵抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y
轴交于点C(0,3),其对称轴l为x=﹣1,
∴,
解得:.
∴二次函数的解析式为y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴顶点坐标为(﹣1,4);
(2)令y=﹣x2﹣2x+3=0,解得x=﹣3或x=1,
∴点A(﹣3,0),B(1,0),
作PD⊥x轴于点D,
∵点P在y=﹣x2﹣2x+3上,
∴设点P(x,﹣x2﹣2x+3)
①∵PA⊥NA,且PA=NA,
∴△PAD≌△ANQ,
∴AQ=PD,
即y=﹣x2﹣2x+3=2,
解得x=﹣1(舍去)或x=﹣﹣1,
∴点P(﹣﹣1,2);
②设P(x,y),则y=﹣x2﹣2x+3,
由于P在第二象限,所以其横坐标满足:﹣3<x<0,
∵S四边形PABC=S△OBC+S△APO+S△OPC,
S△OBC=OB•OC=×3×1=,
S△APO=AO•|y|=×3•y=y=(﹣x2﹣2x+3)=﹣x2﹣3x+,
S△OPC=CO•|x|=×3•(﹣x)=﹣x,
∴S四边形PABC=﹣x2﹣3x+﹣x=6﹣x﹣x2=﹣(x+)2+,
∴当x=﹣时,S四边形PABC最大值=,此时y=﹣x2﹣2x+3=,
所以P(﹣,).
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2019/8/15 17:29:44;用户:15527082918;邮箱:15527082918;学号:27022530
相关文档
- 2019年四川省巴中市恩阳区中考数学2021-11-1223页
- 福建省南平市2020年中考历史模拟试2021-11-1229页
- 2019年四川省凉山市金阳县中考数学2021-11-1225页
- 2019年四川省中考数学模拟试卷(含答2021-11-1223页
- 2020年山东省济南市中考化学全真模2021-11-129页
- 2019年甘肃省兰州市中考数学模拟试2021-11-124页
- 2019年辽宁省葫芦岛市龙港区中考数2021-11-1220页
- 呼和浩特专版2020中考化学复习方案2021-11-125页
- 2019年福建省泉州市永春县中考数学2021-11-1235页
- 河北省石家庄市2020年中考数学模拟2021-11-1229页