2012年贵州省黔南州中考数学试题（含答案） 11页

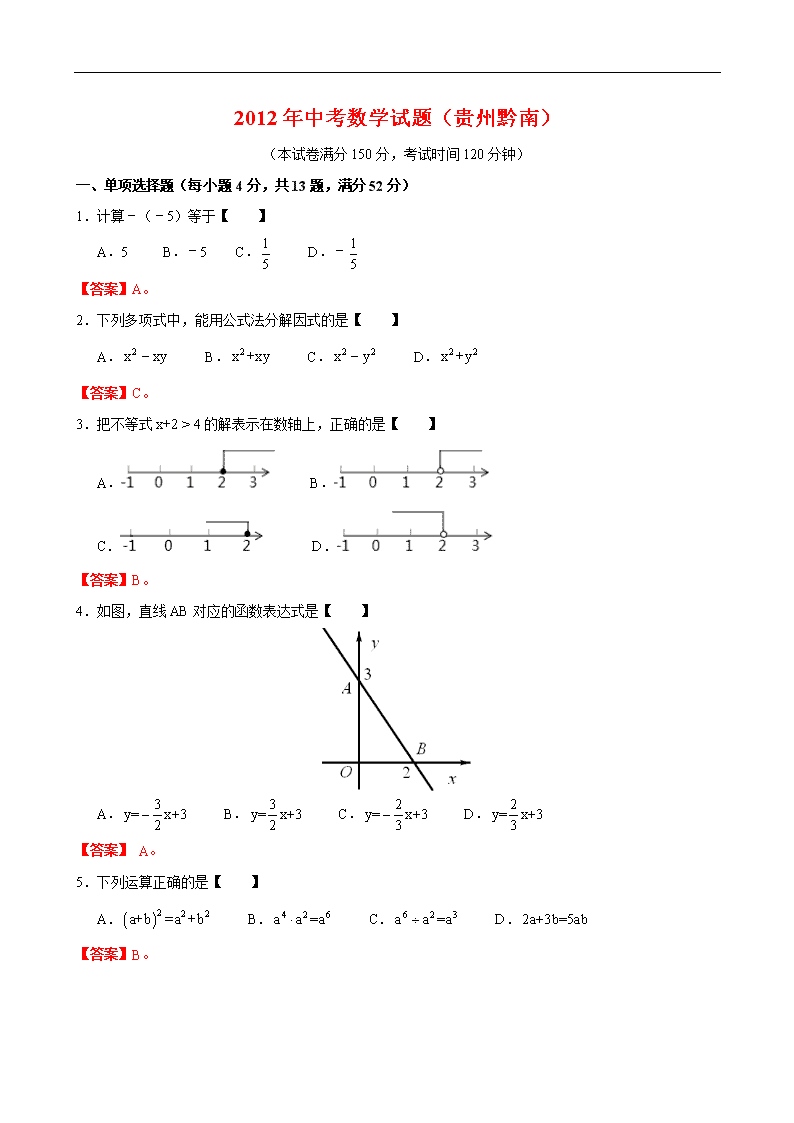
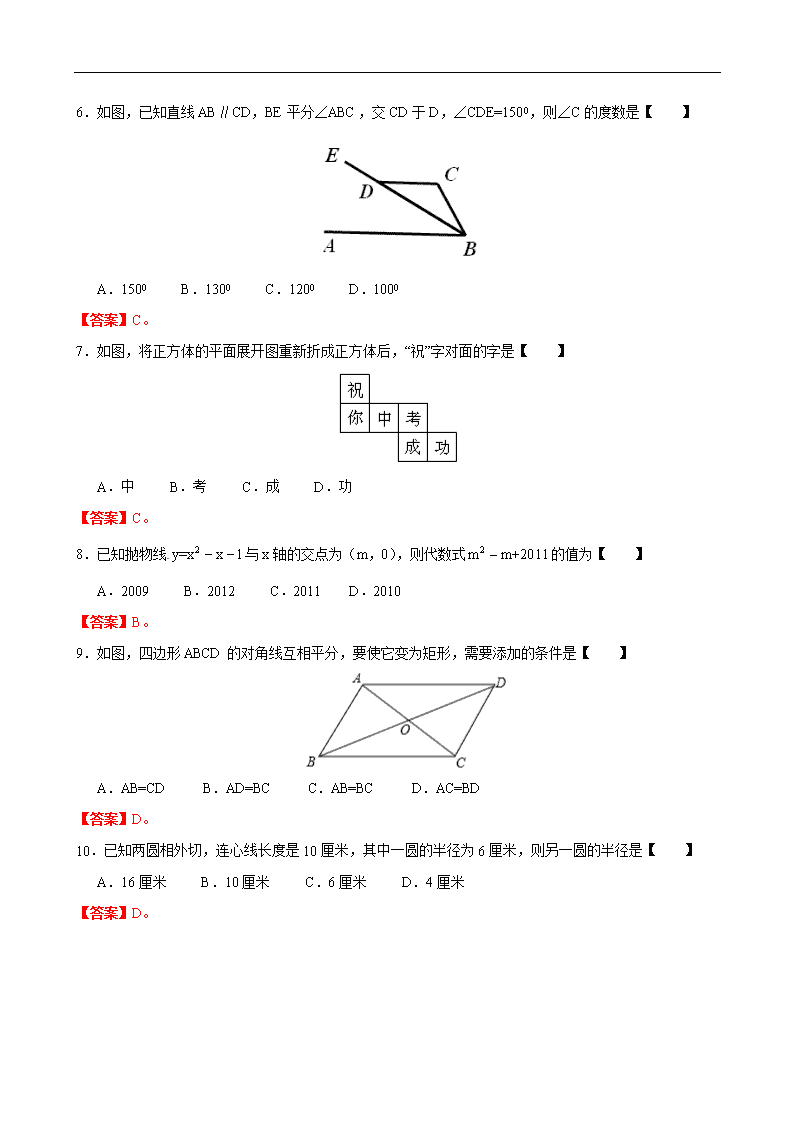
‎2012年中考数学试题（贵州黔南）‎ ‎（本试卷满分150分，考试时间120分钟）‎ 一、单项选择题（每小题4分，共13题，满分52分）‎ ‎1．计算﹣（﹣5）等于【 】‎ A．5 B．﹣5 C． D．﹣‎ ‎【答案】A。‎ ‎2．下列多项式中，能用公式法分解因式的是【 】‎ A． B． C． D．‎ ‎【答案】C。‎ ‎3．把不等式的解表示在数轴上，正确的是【 】‎ A． B． ‎ C． D．‎ ‎【答案】B。‎ ‎4．如图，直线AB对应的函数表达式是【 】‎ A． B． C． D．‎ ‎【答案】 A。 ‎ ‎5．下列运算正确的是【 】‎ A． B． C． D．‎ ‎【答案】B。 ‎ ‎6．如图，已知直线AB∥CD，BE平分∠ABC，交CD于D，∠CDE=1500，则∠C的度数是【 】‎ A．1500 B．1300 C．1200 D．1000‎ ‎【答案】C。‎ ‎7．如图，将正方体的平面展开图重新折成正方体后，“祝”字对面的字是【 】‎ A．中 B．考 C．成 D．功 ‎【答案】C。‎ ‎8．已知抛物线与x轴的交点为（m，0），则代数式的值为【 】‎ A．2009 B．2012 C．2011 D．2010‎ ‎【答案】B。‎ ‎9．如图，四边形ABCD的对角线互相平分，要使它变为矩形，需要添加的条件是【 】‎ A．AB=CD B．AD=BC C．AB=BC D．AC=BD ‎【答案】D。‎ ‎10．已知两圆相外切，连心线长度是10厘米，其中一圆的半径为6厘米，则另一圆的半径是【 】‎ A．16厘米 B．10厘米 C．6厘米 D．4厘米 ‎【答案】D。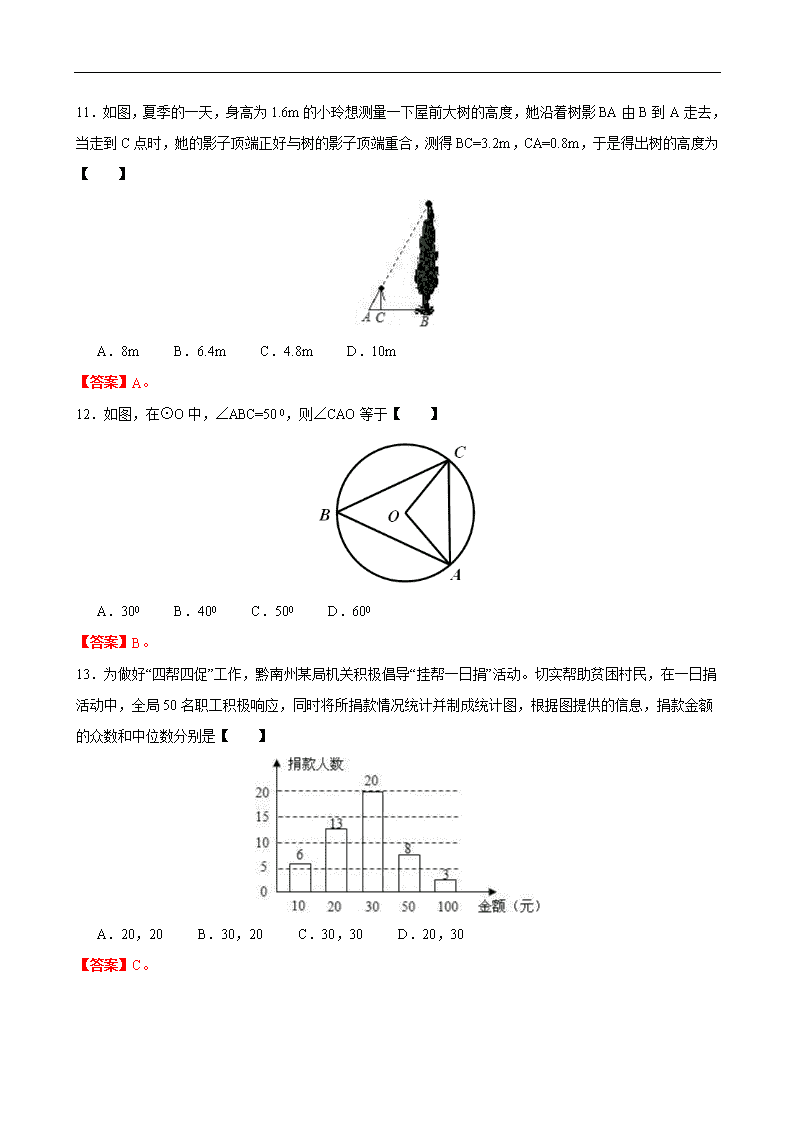‎ ‎11．如图，夏季的一天，身高为1.6m的小玲想测量一下屋前大树的高度，她沿着树影BA由B到A走去，当走到C点时，她的影子顶端正好与树的影子顶端重合，测得BC=3.2m，CA=0.8m，于是得出树的高度为【 】‎ A．8m B．6.4m C．4.8m D．10m ‎【答案】A。‎ ‎12．如图，在⊙O中，∠ABC=500，则∠CAO等于【 】‎ A．300 B．400 C．500 D．600‎ ‎【答案】B。 ‎ ‎13．为做好“四帮四促”工作，黔南州某局机关积极倡导“挂帮一日捐”活动。切实帮助贫困村民，在一日捐活动中，全局50名职工积极响应，同时将所捐款情况统计并制成统计图，根据图提供的信息，捐款金额的众数和中位数分别是【 】‎ A．20，20 B．30，20 C．30，30 D．20，30‎ ‎【答案】C。 ‎ 二、填空题（每题5分，共25分）‎ ‎14．若分式的值为0，则x的值为　 ▲ 　。‎ ‎【答案】1。‎ ‎15． Iphone4手机风靡全世界，苹果公司估计2012年的净利润超过2011年，并有望冲击400亿美元（1美元约合人民币6.3元），用科学计数法表示400亿美元约合人民币　 ▲ 　元（保留两位有效数字）．‎ ‎【答案】2.5×1011。‎ ‎16．都匀市某新修“商业大厦”的一处自动扶梯如图，已知扶梯的长l为10米，该自动扶梯到达的高度h为6米，自动扶梯与地面所成的角为θ，则tanθ的值等于　 ▲ 　。‎ ‎【答案】。‎ ‎17．已知，扇形AOB中，若∠AOB=450，AD=4cm，=3πcm，则图中阴影部分的面积是　 ▲ 　．‎ ‎【答案】cm2。‎ ‎18．如图，四边形ABCD是矩形，A，B两点在x轴的正半轴上，C，D两点在抛物线上，设OA=m（0＜m＜3），矩形ABCD的周长为l，则l 与m的函数解析式为　 ▲ 　。‎ ‎【答案】。‎ 三、解答题（本大题共7个小题，满分73分）‎ ‎19． ‎ ‎（1）计算：；‎ ‎【答案】解：原式=。‎ ‎（2）先化简：，然后求当x=1时，这个代数式的值。‎ ‎【答案】解：原式=。‎ ‎ 当x=1时，原式= ‎ ‎20． “新华网北京5月9日电，近一个月以来，菲律宾在我国中沙黄岩岛海域不断制造事端，袭扰中国渔船，提出国际仲裁，给黄岩岛改名，欲去除岛上与中国有关的标志……”，南海局势紧张，某校针对“黄岩岛事件”在本校学生中做了一次抽样调查，并把调查结果分为三种类型：‎ A.不知道“黄岩岛事件”；[来源:学*科*网]‎ B. 知道“黄岩岛事件”，但不太清楚原因；‎ C. 知道“黄岩岛事件”，并清楚事发原因并表示关注。‎ 图是根据调查结果绘制的部分统计图。‎ 请根据提供的信息回答问题：‎ ‎（1）已知A类学生占被调查学生人数的30%，则被调查学生有多少人？‎ ‎（2）计算B类学生的人数并根据计算结果补全统计图；‎ ‎（3）如果该校共有学生2000人，试估计该校有多少学生知道“黄岩岛事件”，并清楚事发原因并表示关注。‎ ‎【答案】解：（1）∵A类学生有60人，占被调查学生人数的30%，‎ ‎ ∴被调查学生人数为60÷30%=200（人）。‎ ‎ （2）B类学生人数为200－60－30=110（人）。‎ ‎ 补全统计图如下：‎ ‎（3）∵被调查学生中C类学生有30人，占被调查学生人数的，‎ ‎ ∴估计该校2000名中学生知道“黄岩岛事件”，并清楚事发原因并表示关注的人数为：‎ ‎ 2000×=300（人）。‎ ‎21．市“消费者协会”联合市工商局在某中学分别开展打击“地沟油”及“瘦肉精”的食品宣传讲座，小青同学不知该如何听课，最后他决定通过掷硬币来确定，掷硬币规则如下：连续抛掷硬币三次，如果三次正面朝上或三次反面朝上，则小青听两堂讲座；如果两次正面朝上一次反面朝上，则小青去听有关“地沟油”的讲座；如果两次反面朝上一次正面朝上，则小青去听有关“瘦肉精”的讲座。‎ ‎（1）用画树状图的方法表示三次抛掷硬币的所有结果；‎ ‎（2）小青听两堂知识讲座的概率有多大？‎ ‎（3）小青用这个游戏规则去选择听“地沟油”或“瘦肉精”的讲座是否合理？为什么？‎ ‎【答案】解：（1）画树状图如下：‎ ‎ ∴三次抛掷硬币的所有结果有：正正正，正正反，正反正，正反反，反正正，反正反，反反正，反反反8种。‎ ‎ （2）∵由（1）可知，三次抛掷硬币共有8种等可能结果，三次正面朝上或三次反面朝上的有2种，‎ ‎ ∴小青听两堂知识讲座的概率为。‎ ‎ （3）这个游戏规则合理。‎ ‎ ∵两次正面朝上一次反面朝上的结果有3种：正正反，正反正，反正正，‎ ‎ ∴小青去听有关“地沟油”的讲座概率为。‎ ‎∵两次反面朝上一次正面朝上的结果有3种：正反反，反正反，反反正，‎ ‎∴小青去听有关“瘦肉精”的讲座概率为。‎ ‎ ∴小青去听有关“地沟油”的讲座概率=小青去听有关“瘦肉精”的讲座概率。‎ ‎∴这个游戏规则合理。‎ ‎22． 2012年3月25日央视《每周质量播报》报道“毒胶囊”的事件后，全国各大药店的销售都受到不同程度的影响，4月初某种药品的价格大幅度下调，下调后每盒价格是原价格的，原来用60元买到的药品下调后可多买2盒。4月中旬，各部门加大了对胶囊生产监管力度，因此，药品价格4月底开始回升，经过两个月后，药品上调为每盒14.4元。‎ ‎ （1）问该药品的原价格是多少，下调后的价格是多少？‎ ‎ （2）问5、6月份药品价格的月平均增长率是多少？‎ ‎【答案】解：（1）设该药品的原价格是x元/盒，则下调后每盒价格是x元/盒。‎ ‎ 根据题意，得，解得x=15。‎ ‎ 经检验，x=15是原方程的解。‎ ‎ ∴x=15，x=10。‎ ‎ 答：该药品的原价格是15元/盒，则下调后每盒价格是10元/盒。‎ ‎ （2）设5、6月份药品价格的月平均增长率是a，‎ ‎ 根据题意，得，解得（不使题意，舍去）。‎ ‎ 答：5、6月份药品价格的月平均增长率是20%。‎ ‎23．已知，如图，点C在以AB为直径的⊙O上，点D在AB的的延长线上，‎ ‎∠BCD=∠A。‎ ‎（1）求证：CD是⊙O的切线；‎ ‎（2）过点C作CE⊥AB于E。若CE=2，，求AD的长。‎ ‎【答案】解：（1）证明：连接CO，‎ ‎ ∵AB是⊙O直径，∴∠ACO+∠OCB=90°。[来源:学科网ZXXK]‎ ‎∵AO=CO，∴∠ACO =∠A。‎ ‎∵∠BCD=∠A，∴∠BCD +∠OCB=90°，即∠OCD=90°。‎ ‎∴OC⊥CD。‎ 又∵OC是⊙O半径，∴CD为⊙O的切线。‎ ‎（2）∵OC⊥CD于C，∴∠COD +∠D=90°。‎ ‎∵CE⊥AB于E，∴∠COD +∠OCE=90°。∴∠OCE =∠D。[来源:Zxxk.Com]‎ ‎∴cos∠OCE =cosD。‎ 在△OCE中，∠OEC=90°，∴cos∠OCE =。‎ ‎∵，CE=2，∴。∴CO=。‎ ‎∴⊙O的半径为。‎ 在△OCD中，∠OCD=90°，。‎ ‎∴设CD=4k，OD=5k。‎ 根据勾股定理，得，即，解得（已舍负值）。‎ ‎∴OD=。AD=‎ ‎24．如图1，在边长为5的正方形ABCD中，点E、F分别是BC、CD边上的点，且AE⊥EF，BE=2‎ ‎（1）求EC：CF值；‎ ‎（2）延长EF交正方形∠BCD的外角平分线CP于点P（图2），试判断AE与EP大小关系，并说明理由；‎ ‎（3）在图2的AB边上是否存在一点M，使得四边形DMEP是平行四边形？若存在，请给予证明；若不存在，请说明理由。‎ ‎【答案】解：（1）∵AE⊥EF，∴∠BEA+∠CEF=90°。‎ ‎∵四边形ABCD为正方形，∴∠B=∠C=90°。‎ ‎∴∠BAE +∠BEA =90°。∴∠BA E=∠CEF。∴△ABE∽△ECF。‎ ‎∴EC：CF=AB：BE=5：2。‎ ‎（2）在AB上取一点M，使BM=BE，连接ME。‎ ‎∴AM=CE。∴∠BME=45°。∴∠AME=135°。‎ ‎∵CP是外角平分线，∴∠DCP=45°。∴∠ECP=135°。‎ ‎∴∠AME=∠ECP。‎ ‎∵∠AEB+∠BAE=90°，∠AEB+∠CEF=90°，‎ ‎∴∠BAE=∠CEF。∴△AME≌△PCE（ASA）。∴AE=EP。‎ ‎（3）存在，过点D作DM⊥AE交AB于点M，则此时M使得四边形DMEP是平行四边形。证明如下：‎ ‎ ∵DM⊥AE，∴∠ADM=90°－∠DAE。‎ ‎ ∵四边形ABCD为正方形，∴AB=AD，∠B=∠BAD=90°。‎ ‎ ∴∠BAE=90°－∠DAE。∴∠BAE=∠ADM。‎ ‎ ∴△BAE≌△ADM（ASA）。∴AD=DM。‎ ‎ 由（2）AE=EP，得DM= EP。[来源:学,科,网Z,X,X,K]‎ ‎ 双∵DM⊥AE，AE⊥EF，∴DM∥ EP。∴四边形DMEP是平行四边形。‎ ‎25．如图，对称轴为ｘ=3的抛物线与ｘ轴相交于点B、O。‎ ‎（1）求抛物线的解析式，并求出顶点A的坐标；‎ ‎（2）连结AB，把AB所在的直线平移，使它经过原点O，得到直线ｌ。点P是ｌ上一动点。设以点A、B、O、P为顶点的四边形面积为S，点P的横坐标为ｔ，当0＜S≤18时，求ｔ的取值范围；‎ ‎（3）在（2）的条件下，当ｔ取最大值时，抛物线上是否存在点Q，使△OPQ为直角三角形且OP为直角边。若存在，直接写岀点Q的坐标；若不存在，说明理由。（平面几何有个结论：如果两直线垂直，那么它们的斜率的乘积为－1，坐标轴所在直线除外）‎ ‎【答案】解：（1）∵点B与O（0，0）关于x=3对称，∴点B坐标为（6，0）。‎ 将点B坐标代入得：36a+12=0。∴a=。[来源:Zxxk.Com]‎ ‎∴抛物线解析式为。‎ 当x=3时，。∴顶点A坐标为（3，3）。‎ ‎（2）设直线AB解析式为y=kx+b，‎ ‎∵A（3，3），B（6，0），∴，解得。‎ ‎∴直线AB解析式为y=－x+6。‎ ‎∵直线l∥AB且过点O，∴直线l解析式为y=－x。‎ ‎∵点P是l上一动点且横坐标为t，∴点P坐标为（t，－t）。‎ 当P在第四象限时（t＞0），则 ‎。‎ ‎∵0＜S≤18，∴0＜9+3t≤18。∴－3＜t≤3。‎ 又t＞0，∴0＜t≤3。‎ 当P在第二象限时（t＜0），作PM⊥x轴于M。‎ 设对称轴与x轴交点为N，则 ‎。‎ ‎∵0＜S≤18，∴0＜－3t+9≤18。∴－3≤t＜3。‎ 又t＜0，∴-3≤t＜0。∴t的取值范围是－3≤t＜0或0＜t≤3。‎ ‎（3）存在。点Q坐标为（3，3）或（6，0）或（－3，－9）。‎