2018年湖南省湘潭市中考数学试卷含答案 18页

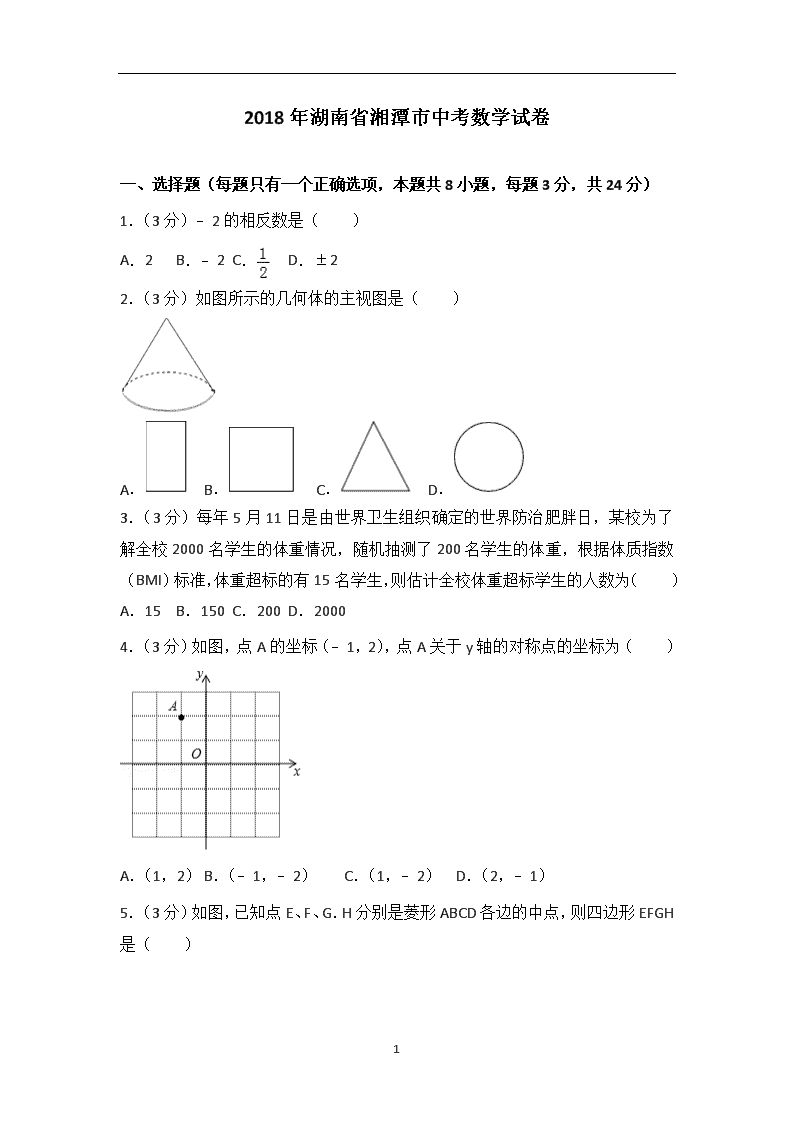
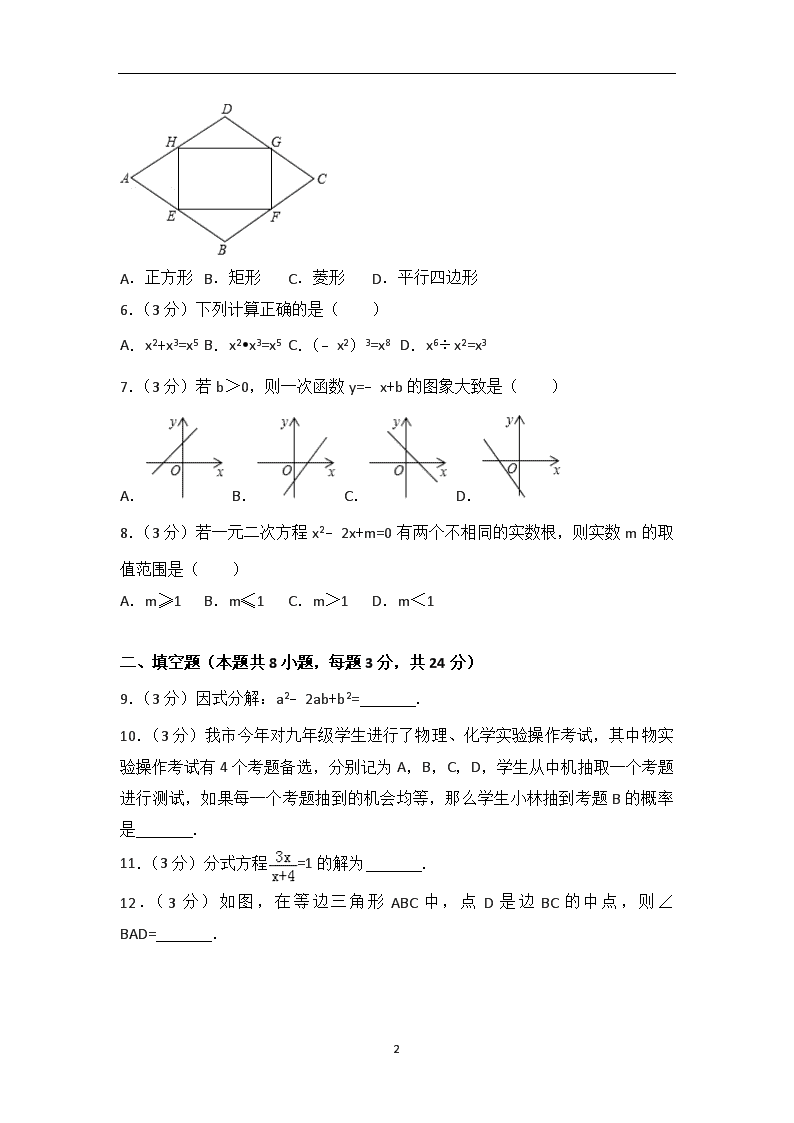
‎2018年湖南省湘潭市中考数学试卷 ‎　‎ 一、选择题（每题只有一个正确选项，本题共8小题，每题3分，共24分）‎ ‎1．（3分）﹣2的相反数是（　　）‎ A．2 B．﹣2 C． D．±2‎ ‎2．（3分）如图所示的几何体的主视图是（　　）‎ A． B． C． D．‎ ‎3．（3分）每年5月11日是由世界卫生组织确定的世界防治肥胖日，某校为了解全校2000名学生的体重情况，随机抽测了200名学生的体重，根据体质指数（BMI）标准，体重超标的有15名学生，则估计全校体重超标学生的人数为（　　）‎ A．15 B．150 C．200 D．2000‎ ‎4．（3分）如图，点A的坐标（﹣1，2），点A关于y轴的对称点的坐标为（　　）‎ A．（1，2） B．（﹣1，﹣2） C．（1，﹣2） D．（2，﹣1）‎ ‎5．（3分）如图，已知点E、F、G．H分别是菱形ABCD各边的中点，则四边形EFGH是（　　）‎ 18‎ A．正方形 B．矩形 C．菱形 D．平行四边形 ‎6．（3分）下列计算正确的是（　　）‎ A．x2+x3=x5 B．x2•x3=x5 C．（﹣x2）3=x8 D．x6÷x2=x3‎ ‎7．（3分）若b＞0，则一次函数y=﹣x+b的图象大致是（　　）‎ A． B． C． D．‎ ‎8．（3分）若一元二次方程x2﹣2x+m=0有两个不相同的实数根，则实数m的取值范围是（　　）‎ A．m≥1 B．m≤1 C．m＞1 D．m＜1‎ ‎　‎ 二、填空题（本题共8小题，每题3分，共24分）‎ ‎9．（3分）因式分解：a2﹣2ab+b2=　 　．‎ ‎10．（3分）我市今年对九年级学生进行了物理、化学实验操作考试，其中物实验操作考试有4个考题备选，分别记为A，B，C，D，学生从中机抽取一个考题进行测试，如果每一个考题抽到的机会均等，那么学生小林抽到考题B的概率是　 　．‎ ‎11．（3分）分式方程=1的解为　 　．‎ ‎12．（3分）如图，在等边三角形ABC中，点D是边BC的中点，则∠BAD=　 　．‎ 18‎ ‎13．（3分）如图，AB是⊙O的切线，点B为切点，若∠A=30°，则∠AOB=　 　．‎ ‎14．（3分）如图，点E是AD延长线上一点，如果添加一个条件，使BC∥AD，则可添加的条件为　 　．（任意添加一个符合题意的条件即可）‎ ‎15．（3分）《九章算术》是我国古代最重要的数学著作之一，在“匀股”章中记载了一道“折竹抵地”问题：“今有竹高一丈，末折抵地，去本三尺，问折者高几何？”翻译成数学问题是：如图所示，△ABC中，∠ACB=90°，AC+AB=10，BC=3，求AC的长，如果设AC=x，则可列方程为　 　．‎ ‎16．（3分）阅读材料：若ab=N，则b=logaN，称b为以a为底N的对数，例如23=8，则log28=log223=3．根据材料填空：log39=　 　．‎ ‎　‎ 三、解答题（本题共10题，102分）‎ ‎17．（6分）计算：|﹣5|+（﹣1）2﹣（）﹣1﹣．‎ 18‎ ‎18．（6分）先化简，再求值：（1+）÷．其中x=3．‎ ‎19．（6分）随看航母编队的成立，我国海军日益强大，2018年4月12日，中央军委在南海海域降重举行海上阅兵，在阅兵之前我军加强了海上巡逻，如图，我军巡逻舰在某海域航行到A处时，该舰在观测点P的南偏东45°的方向上，且与观测点P的距离PA为400海里；巡逻舰继续沿正北方向航行一段时间后，到达位于观测点P的北偏东30°方向上的B处，问此时巡逻舰与观测点P的距离PB为多少每里？（参考数据：≈1.414，≈1.732，结果精确到1海里）．‎ ‎20．（6分）为进一步深化基教育课程改革，构建符合素质教育要求的学校课程体系，某学校自主开发了A书法、B阅读，C足球，D器乐四门校本选修课程供学生选择，每门课程被选到的机会均等．‎ ‎（1）学生小红计划选修两门课程，请写出所有可能的选法；‎ ‎（2）若学生小明和小刚各计划送修一门课程，则他们两人恰好选修同一门课程的概率为多少？‎ ‎21．（6分）今年我市将创建全国森林城市，提出了“共建绿色城”的倡议．某校积极响应，在3月12日植树节这天组织全校学生开展了植树活动，校团委对全校各班的植树情况道行了统计，绘制了如图所示的两个不完整的统计图．‎ 18‎ ‎（1）求该校的班级总数；‎ ‎（2）将条形统计图补充完整；‎ ‎（3）求该校各班在这一活动中植树的平均数．‎ ‎22．（6分）如图，在正方形ABCD中，AF=BE，AE与DF相交于于点O．‎ ‎（1）求证：△DAF≌△ABE；‎ ‎（2）求∠AOD的度数．‎ ‎23．（8分）湘潭市继2017年成功创建全国文明城市之后，又准备争创全国卫生城市．某小区积极响应，决定在小区内安装垃圾分类的温馨提示牌和垃圾箱，若购买2个温馨提示牌和3个垃圾箱共需550元，且垃圾箱的单价是温馨提示牌单价的3倍．‎ ‎（1）求温馨提示牌和垃圾箱的单价各是多少元？‎ ‎（2）该小区至少需要安放48个垃圾箱，如果购买温馨提示牌和垃圾箱共100个，且费用不超过10000元，请你列举出所有购买方案，并指出哪种方案所需资金最少？最少是多少元？‎ ‎24．（8分）如图，点M在函数y=（x＞0）的图象上，过点M分别作x轴和y轴的平行线交函数y=（x＞0）的图象于点B、C．‎ ‎（1）若点M的坐标为（1，3）．‎ ‎①求B、C两点的坐标；‎ ‎②求直线BC的解析式；‎ ‎（2）求△BMC的面积．‎ 18‎ ‎25．（10分）如图，AB是以O为圆心的半圆的直径，半径CO⊥AO，点M是上的动点，且不与点A、C、B重合，直线AM交直线OC于点D，连结OM与CM．‎ ‎（1）若半圆的半径为10．‎ ‎①当∠AOM=60°时，求DM的长；‎ ‎②当AM=12时，求DM的长．‎ ‎（2）探究：在点M运动的过程中，∠DMC的大小是否为定值？若是，求出该定值；若不是，请说明理由．‎ ‎26．（10分）如图，点P为抛物线y=x2上一动点．‎ ‎（1）若抛物线y=x2是由抛物线y=（x+2）2﹣1通过图象平移得到的，请写出平移的过程；‎ ‎（2）若直线l经过y轴上一点N，且平行于x轴，点N的坐标为（0，﹣1），过点P作PM⊥l于M．‎ ‎①问题探究：如图一，在对称轴上是否存在一定点F，使得PM=PF恒成立？若存在，求出点F的坐标：若不存在，请说明理由．‎ ‎②问题解决：如图二，若点Q的坐标为（1.5），求QP+PF的最小值．‎ 18‎ ‎　‎ 18‎ ‎2018年湖南省湘潭市中考数学试卷 参考答案与试题解析 ‎　‎ 一、选择题（每题只有一个正确选项，本题共8小题，每题3分，共24分）‎ ‎1．‎ ‎【解答】解：﹣2的相反数是：﹣（﹣2）=2．‎ 故选：A．‎ ‎　‎ ‎2．‎ ‎【解答】解：该几何体的主视图是三角形，‎ 故选：C．‎ ‎　‎ ‎3．‎ ‎【解答】解：估计全校体重超标学生的人数为2000×=150人，‎ 故选：B．‎ ‎　‎ ‎4．‎ ‎【解答】解：点A的坐标（﹣1，2），点A关于y轴的对称点的坐标为：（1，2）．‎ 故选：A．‎ 18‎ ‎　‎ ‎5．‎ ‎【解答】解：连接AC、BD．AC交FG于L．‎ ‎∵四边形ABCD是菱形，‎ ‎∴AC⊥BD，‎ ‎∵DH=HA，DG=GC，‎ ‎∴GH∥AC，HG=AC，‎ 同法可得：EF=AC，EF∥AC，‎ ‎∴GH=EF，GH∥EF，‎ ‎∴四边形EFGH是平行四边形，‎ 同法可证：GF∥BD，‎ ‎∴∠OLF=∠AOB=90°，‎ ‎∵AC∥GH，‎ ‎∴∠HGL=∠OLF=90°，‎ ‎∴四边形EFGH是矩形．‎ 故选：B．‎ ‎　‎ 18‎ ‎6．‎ ‎【解答】解：A、x2+x3，无法计算，故此选项错误；‎ B、x2•x3=x5，正确；‎ C、（﹣x2）3=﹣x6，故此选项错误；‎ D、x6÷x2=x4，故此选项错误；‎ 故选：B．‎ ‎　‎ ‎7．‎ ‎【解答】解：∵一次函数y=x+b中k=﹣1＜0，b＞0，‎ ‎∴一次函数的图象经过一、二、四象限，‎ 故选：C．‎ ‎　‎ ‎8．‎ ‎【解答】解：∵方程x2﹣2x+m=0有两个不相同的实数根，‎ ‎∴△=（﹣2）2﹣4m＞0，‎ 解得：m＜1．‎ 故选：D．‎ ‎　‎ 二、填空题（本题共8小题，每题3分，共24分）‎ ‎9．‎ ‎【解答】解：原式=（a﹣b）2‎ 故答案为：（a﹣b）2‎ ‎　‎ ‎10．‎ ‎【解答】解：∵物实验操作考试有4个考题备选，且每一个考题抽到的机会均等，‎ ‎∴学生小林抽到考题B的概率是：．‎ 故答案是：．‎ 18‎ ‎　‎ ‎11．‎ ‎【解答】解：两边都乘以x+4，得：3x=x+4，‎ 解得：x=2，‎ 检验：x=2时，x+4=6≠0，‎ 所以分式方程的解为x=2，‎ 故答案为：x=2．‎ ‎　‎ ‎12．‎ ‎【解答】解：∵△ABC是等边三角形，‎ ‎∴∠BAC=60°，AB=AC．‎ 又点D是边BC的中点，‎ ‎∴∠BAD=∠BAC=30°．‎ 故答案是：30°．‎ ‎　‎ ‎13．‎ ‎【解答】解：∵AB是⊙O的切线，‎ ‎∴∠OBA=90°，‎ ‎∴∠AOB=90°﹣∠A=60°，‎ 故答案为：60°．‎ ‎　‎ ‎14．‎ ‎【解答】解：若∠A+∠ABC=180°，则BC∥AD；‎ 若∠C+∠ADC=180°，则BC∥AD；‎ 若∠CBD=∠ADB，则BC∥AD；‎ 若∠C=∠CDE，则BC∥AD；‎ 故答案为：∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE．（答案不唯一）‎ ‎　‎ 18‎ ‎15．‎ ‎【解答】解：设AC=x，‎ ‎∵AC+AB=10，‎ ‎∴AB=10﹣x．‎ ‎∵在Rt△ABC中，∠ACB=90°，‎ ‎∴AC2+BC2=AB2，即x2+32=（10﹣x）2．‎ 故答案为：x2+32=（10﹣x）2．‎ ‎　‎ ‎16．‎ ‎【解答】解：∵32=9，‎ ‎∴log39=log332=2．‎ 故答案为2．‎ ‎　‎ 三、解答题（本题共10题，102分）‎ ‎17．‎ ‎【解答】解：原式=5+1﹣3﹣2=1．‎ ‎　‎ ‎18．‎ ‎【解答】解：（1+）÷‎ ‎=×‎ ‎=x+2．‎ 当x=3时，原式=3+2=5．‎ ‎　‎ ‎19．‎ ‎【解答】解：在△APC中，∠ACP=90°，∠APC=45°，则AC=PC．‎ ‎∵AP=400海里，‎ ‎∴由勾股定理知，AP2=AC2+PC2=2PC2，即4002=2PC2，‎ 18‎ 故PC=200海里．‎ 又∵在直角△BPC中，∠PCB=90°，∠BPC=60°，‎ ‎∴PB==2PC=400≈565.6（海里）．‎ 答：此时巡逻舰与观测点P的距离PB约为565.6每里．‎ ‎　‎ ‎20．‎ ‎【解答】解：（1）画树状图为：‎ 共有12种等可能的结果数；‎ ‎（2）画树状图为：‎ 共有16种等可能的结果数，其中他们两人恰好选修同一门课程的结果数为4，‎ 所以他们两人恰好选修同一门课程的概率==．‎ ‎　‎ ‎21．‎ ‎【解答】解：（1）该校的班级总数=3÷25%=12，‎ 答：该校的班级总数是12；‎ ‎（2）植树11颗的班级数：12﹣1﹣2﹣3﹣4=2，如图所示：‎ ‎（3）（1×8+2×9+2×11+3×12+4×15）÷12=12（颗），‎ 答：该校各班在这一活动中植树的平均数约是12颗数．‎ ‎　‎ 18‎ ‎22．‎ ‎【解答】（1）证明：∵四边形ABCD是正方形，‎ ‎∴∠DAB=∠ABC=90°，AD=AB，‎ 在△DAF和△ABE中，，‎ ‎∴△DAF≌△ABE（SAS），‎ ‎（2）由（1）知，△DAF≌△ABE，‎ ‎∴∠ADF=∠BAE，‎ ‎∵∠ADF+∠DAO=∠BAE+∠DAO=∠DAB=90°，‎ ‎∴∠AOD=180°﹣（∠ADF+DAO）=90°．‎ ‎　‎ ‎23．‎ ‎【解答】解：（1）设温情提示牌的单价为x元，则垃圾箱的单价为3x元，‎ 根据题意得，2x+3×3x=550，‎ ‎∴x=50，‎ 经检验，符合题意，‎ ‎∴3x=150元，‎ 即：温馨提示牌和垃圾箱的单价各是50元和150元；‎ ‎（2）设购买温情提示牌y个（y为正整数），则垃圾箱为（100﹣y）个，‎ 根据题意得，意，，‎ ‎∴≤y≤52，‎ ‎∵y为正整数，‎ ‎∴y为42，43，44，45，46，47，48，49，50，51，52，共11中方案；‎ 即：温馨提示牌42个，垃圾箱58个，温馨提示牌43个，垃圾箱57个，温馨提示牌44个，垃圾箱56个，‎ 温馨提示牌45个，垃圾箱55个，温馨提示牌46个，垃圾箱54个，温馨提示牌47个，垃圾箱53个，‎ 18‎ 温馨提示牌48个，垃圾箱52个，温馨提示牌49个，垃圾箱51个，温馨提示牌50个，垃圾箱50个，‎ 温馨提示牌51个，垃圾箱49个，温馨提示牌52个，垃圾箱48个，‎ 根据题意，费用为30y+150（100﹣y）=﹣120y+15000，‎ 当y=52时，所需资金最少，最少是8760元．‎ ‎　‎ ‎24．‎ ‎【解答】解：（1）①∵点M的坐标为（1，3）‎ 且B、C函数y=（x＞0）的图象上 ‎∴点C横坐标为1，纵坐标为1‎ 点B纵坐标为3，横坐标为 ‎∴点C坐标为（1，1），点B坐标为（，3）‎ ‎②设直线BC解析式为y=kx+b 把B、C点坐标代入得 解得 ‎∴直线BC解析式为：y=﹣3x+4‎ ‎（2）设点M坐标为（a，b）‎ ‎∵点M在函数y=（x＞0）的图象上 ‎∴ab=3‎ 由（1）点C坐标为（a，），B点坐标为（，b）‎ ‎∴BM=a﹣，MC=b﹣‎ ‎∴S△BMC=‎ ‎　‎ 18‎ ‎25．‎ ‎【解答】解：（1）①当∠AOM=60°时，‎ ‎∵OM=OA，‎ ‎∴△AMO是等边三角形，‎ ‎∴∠A=∠MOA=60°，‎ ‎∴∠MOD=30°，∠D=30°，‎ ‎∴DM=OM=10‎ ‎②过点M作MF⊥OA于点F，‎ 设AF=x，‎ ‎∴OF=10﹣x，‎ ‎∵AM=12，OA=OM=10，‎ 由勾股定理可知：122﹣x2=102﹣（10﹣x）2‎ ‎∴x=，‎ ‎∴AF=，‎ ‎∵MF∥OD，‎ ‎∴△AMF∽△ADO，‎ ‎∴，‎ ‎∴，‎ ‎∴AD=‎ ‎∴MD=AD﹣AM=‎ ‎（2）当点M位于之间时，‎ 连接BC，‎ ‎∵C是的重点，‎ ‎∴∠B=45°，‎ ‎∵四边形AMCB是圆内接四边形，‎ 18‎ 此时∠CMD=∠B=45°，‎ 当点M位于之间时，‎ 连接BC，‎ 由圆周角定理可知：∠CMD=∠B=45°‎ 综上所述，∠CMD=45°‎ ‎　‎ ‎26．‎ ‎【解答】解：（1）∵抛物线y=（x+2）2﹣1的顶点为（﹣2，﹣1）‎ ‎∴抛物线y=（x+2）2﹣1的图象向上平移1个单位，再向右2个单位得到抛物线y=x2的图象．‎ ‎（2）①存在一定点F，使得PM=PF恒成立．‎ 如图一，过点P作PB⊥y轴于点B 18‎ 设点P坐标为（a，a2）‎ ‎∴PM=PF=a2+1‎ ‎∵PB=a ‎∴Rt△PBF中 BF=‎ ‎∴OF=1‎ ‎∴点F坐标为（0，1）‎ ‎②由①，PM=PF QP+PF的最小值为QP+QM的最小值 当Q、P、M三点共线时，QP+QM有最小值为点Q纵坐标5．‎ ‎∴QP+PF的最小值为5．‎ ‎　‎ 18‎