云南省2021年中考数学模拟试题及答案(四) 16页

‎2021年云南省初中学业水平考试 数学模拟卷(四)‎ ‎(考试时间：120分钟　满分：120分)‎ ‎　一、填空题(本大题共6小题，每小题3分，共18分)‎ ‎1．如果风车顺时针旋转45°记作＋45°，那么逆时针旋转60°记作__－60°__．‎ ‎2．如图，已知∠1＋∠2＝180°，∠3＝75°，则∠4＝__105°__．‎ ‎3．使二次根式有意义的x的取值范围是__x≤2__．‎ ‎4．分解因式：12a2b－3b＝__3b(2a＋1)(2a－1)__．‎ ‎5．若关于x的一元二次方程(x＋2)2＝n有实数根，则n的取值范围是__n≥0__．‎ ‎6．在矩形ABCD中，AB＝9 cm，E是直线CD上一点，连接AC，BE，若AC与BE交于点F且DE＝3 cm，则EF∶BE的值是__4∶7或2∶5__．‎ 二、选择题(本大题共8小题，每小题只有一个正确选项，每小题4分，共32分)‎ ‎7．华为Mate30 5G系列是一款相当火爆的5G国产手机，它采用的麒麟990 5G芯片在指甲盖大小的尺寸上集成了103亿个晶体管，将103亿用科学记数法表示为 (C)‎ A．1.03×109 B．10.3×109‎ C．1.03×1010 D．1.03×1011‎ ‎8．由4个相同的小正方体组成的几何体如图所示，则它的左视图是(D)‎ ‎　　　‎ ‎9．若一个多边形的每个内角均为120°，则该多边形是 (C)‎ A．四边形 B．五边形 C．六边形 D．七边形 ‎10．下列按照一定规律排列一组图形，其中图形①中共有2个小三角形，图形②中共有6个小三角形，图形③中共有11个小三角形，图形④中共有17个小三角形，….按此规律，图形⑧中共有n个小三角形，这里的n＝ (C)‎ A．32 B．41 C．51 D．53‎ ‎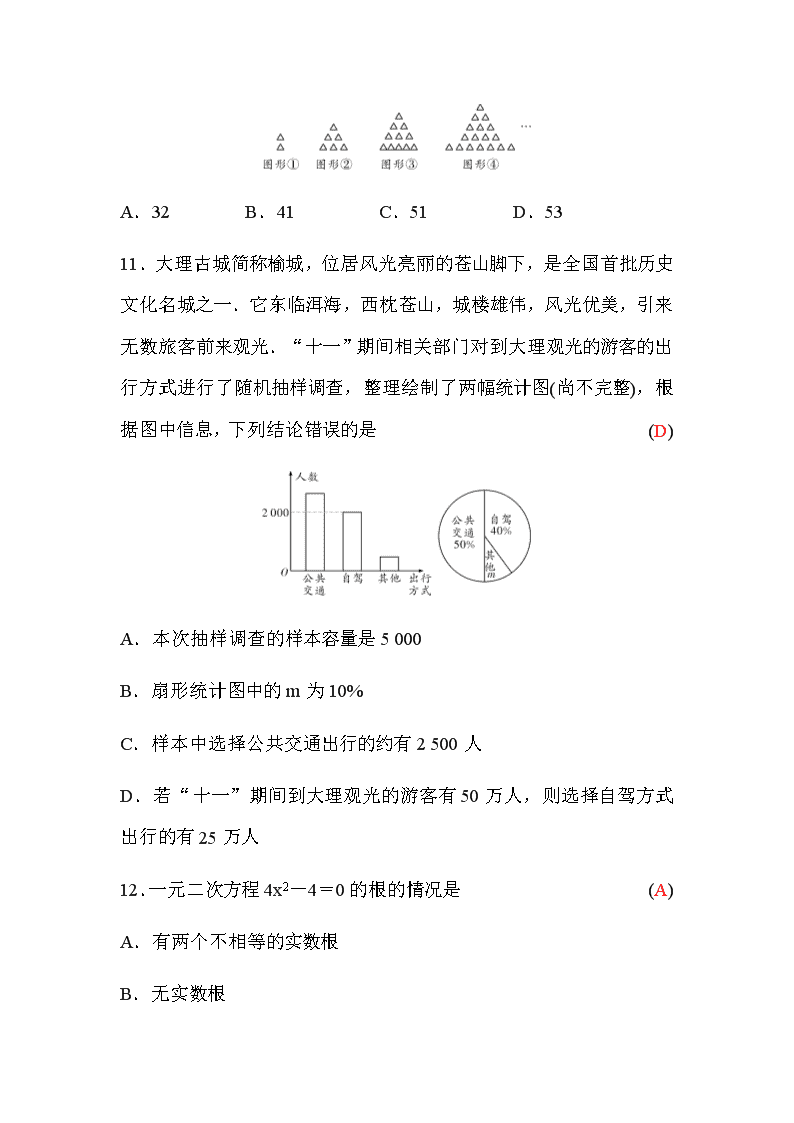11．大理古城简称榆城，位居风光亮丽的苍山脚下，是全国首批历史文化名城之一．它东临洱海，西枕苍山，城楼雄伟，风光优美，引来无数旅客前来观光．“十一”期间相关部门对到大理观光的游客的出行方式进行了随机抽样调查，整理绘制了两幅统计图(尚不完整)，根据图中信息，下列结论错误的是 (D)‎ A．本次抽样调查的样本容量是5 000‎ B．扇形统计图中的m为10%‎ C．样本中选择公共交通出行的约有2 500人 D．若“十一”期间到大理观光的游客有50万人，则选择自驾方式出行的有25万人 ‎12．一元二次方程4x2－4＝0的根的情况是 (A)‎ A．有两个不相等的实数根 B．无实数根 C．有两个相等的实数根 D．无法确定 ‎13．已知⊙O的半径为6，弦AB与半径相等，则用扇形OAB围成的圆锥的底面半径为 (C)‎ A．1或4 B．4 C．1或5 D．5‎ ‎14．若关于x的分式方程＝＋5的解为正数，则m的取值范围为 (D)‎ A．m＜－10 B．m≤－10‎ C．m≥－10且m≠－6 D．m＞－10且m≠－6‎ 三、解答题(本大题共9小题，共70分)‎ ‎15．(本小题满分6分)计算：‎ ＋(π＋)0－()－1·sin 45°.‎ 解：原式＝－1＋1－2× ‎＝－1＋1－ ‎＝0.‎ ‎16．(本小题满分6分)如图，点A，D，C，F在同一条直线上，AD＝CF，AB＝DE，AB∥DE.求证：BC＝EF.‎ 证明：∵AB∥DE，∴∠A＝∠EDF，‎ ‎∵AC＝AD＋DC，DF＝DC＋CF，且AD＝CF，‎ ‎∴AC＝DF.‎ 在△ABC和△DEF中，‎ ‎∴△ABC≌△DEF(SAS)，‎ ‎∴BC＝EF.‎ ‎17．(本小题满分8分)停课不停学，疫情期间，八(1)班30位同学参加运动线上打卡，张老师为了鼓励同学们积极锻炼，统计了这30人15天的打卡次数如表：‎ 打卡次数 ‎7‎ ‎8‎ ‎9‎ ‎14‎ ‎15‎ 人数 ‎6‎ ‎9‎ ‎6‎ ‎3‎ ‎6‎ ‎(1)直接写出打卡次数的众数和中位数；‎ ‎(2)求所有同学打卡次数的平均数；‎ ‎(3)为了调动同学们锻炼的积极性，‎ 张老师决定制定一个打卡奖励标准，凡打卡次数达到或超过这个标准的同学将获得奖励．请你根据(1)、(2)中所求的统计量，帮助张老师制定一个较为合理的打卡奖励标准，并说明理由．‎ 解：(1)8次的人数最多，众数为8次；‎ 共30人，‎ 所有同学打卡次数从小到大排列第15个、第16个数分别为8次，9次，‎ 中位数为(8＋9)÷2＝8.5(次).‎ ‎(2)平均数为(7×6＋8×9＋9×6＋14×3＋15×6)÷30＝10(次).‎ ‎(3)为了调动同学们锻炼的积极性，‎ 打卡奖励标准可以定为所有同学打卡次数的中位数．‎ 因为共有30人，9次以上(含9次)的有15人，等于总数的一半．‎ ‎18．(本小题满分6分)某市为进一步缓解交通拥堵现象，决定修建一条从市中心到飞机场的轻轨铁路．实际施工时，每月的工效比原计划提高了20%，结果提前3个月完成这一工程．求原计划完成这一工程的时间是多少个月？‎ 解：设原计划完成这一工程的时间为x个月，‎ 由题意，得(1＋20%)·＝，‎ 解得x＝18.‎ 经检验，x＝18是原方程的解．‎ 答：原计划完成这一工程的时间是18个月．‎ ‎19．(本小题满分7分)某公司有甲、乙、丙三辆车去南京，它们出发的先后顺序随机．张先生和李先生乘坐该公司的车去南京出差，但有不同的需求．‎ 请用所学概率知识解决下列问题：‎ ‎(1)写出这三辆车按先后顺序出发的所有可能结果；‎ ‎(2)两人中，谁乘坐到甲车的可能性大？请说明理由．‎ 解：(1)甲、乙、丙；甲、丙、乙；乙、甲、丙；‎ 乙、丙、甲；丙、甲、乙；丙、乙、甲；共6种．‎ ‎(2)由(1)可知张先生坐到甲车有两种可能，乙、丙、甲，丙、乙、甲，‎ 则张先生坐到甲车的概率是＝；‎ 由(1)可知李先生坐到甲车有两种可能，甲、乙、丙，甲、丙、乙，‎ 则李先生坐到甲车的概率是＝；‎ 所以两人坐到甲车的可能性一样．‎ ‎20．(本小题满分8分)已知点A(1，1)在抛物线y＝x2＋(2m＋1)x－n－1上 ‎(1)求m，n的关系式；‎ ‎(2)若该抛物线的顶点在x轴上，求出它的解析式．‎ 解：(1)将点A(1，1)代入y＝x2＋(2m＋1)x－n－1得 ‎1＝12＋(2m＋1)×1－n－1，整理得n＝2m，‎ 故m，n的关系式为n＝2m.‎ ‎(2)∵抛物线的顶点在x轴上，‎ ‎∴＝0，‎ ‎∵n＝2m，‎ ‎∴代入上式化简得4m2＋12m＋5＝0，‎ 解得m＝－或m＝－.‎ 当m＝－时，n＝－5，抛物线的解析式为 y＝x2－4x＋4，‎ 当m＝－时，n＝－1，抛物线的解析式为y＝x2，‎ ‎∴抛物线的解析式为y＝x2或y＝x2－4x＋4.‎ ‎21．(本小题满分8分)某公司为了宣传一种新产品，在某地先后举行40场产品促销会，已知该产品每台成本为10万元，设第x场产品的销售量为y(台)，在销售过程中获得以下信息：‎ 信息1：已知第一场促销会销售产品49台，然后每增加一场，产品就少卖出1台；‎ 信息2：产品的每场销售单价p(万元)由基本价和浮动价两部分组成，其中基本价保持不变，第1场～第20场浮动价与销售场次x成正比，第21场～第40场浮动价与销售场次x成反比，经过统计，得到如下数据：‎ x(场)‎ ‎3‎ ‎10‎ ‎25‎ p(万元)‎ ‎10.6‎ ‎12‎ ‎14.2‎ ‎(1)求y与x之间满足的函数关系式；‎ ‎(2)当产品销售单价为13万元时，求销售场次是第几场？‎ ‎(3)在这40场产品促销会中，哪一场获得的利润最大，最大利润是多少？‎ 解：(1)由题意，可得y与x的函数关系式为y＝50－x.‎ ‎(2)设基本价为b，‎ ‎①第1场～第20场，设p与x的函数关系式为p＝ax＋b；‎ 依题意得解得 ‎∴p＝x＋10，当p＝13时，x＋10＝13，解得x＝15；‎ ‎②第21场～第40场，设p与x的函数关系式为p＝＋b，即p＝＋10.‎ 依题意得14.2＝＋10，解得m＝105，‎ ‎∴p＝＋10，‎ 当p＝13时，＋10＝13，解得x＝35.‎ 故当产品销售单价为13万元时，销售场次是第15场和第35场．‎ ‎(3)设每场获得的利润为w(万元).‎ ‎①当1≤x≤20时，w＝(x＋10－10)(50－x)＝－x2＋10x＝－(x－25)2＋125，‎ ‎∵在对称轴的左侧，w随x的增大而增大，‎ ‎∴当x＝20时，w最大，最大利润为 ‎－(20－25)2＋125＝120(万元)；‎ ‎②当21≤x≤40时，‎ w＝(＋10－10)(50－x)＝－105，‎ ‎∵w随x的增大而减小，‎ ‎∴当x＝21时，w最大，最大利润为 －105＝145(万元)，‎ ‎∵120＜145，‎ ‎∴在这40场产品促销会中，第21场获得的利润最大，最大利润为145万元．‎ ‎22．(本小题满分9分)如图，AB为⊙O的直径，射线AD交⊙O于点F，点C为劣弧的中点，过点C作CE⊥AD，垂足为E，连接AC.‎ ‎(1)求证：CE是⊙O的切线；‎ ‎(2)若∠BAC＝30°，AB＝4，求阴影部分的面积．‎ ‎(1)证明：连接BF，‎ ‎∵AB是⊙O的直径，‎ ‎∴∠AFB＝90°，即BF⊥AD，‎ ‎∵CE⊥AD，∴BF∥CE.‎ 连接OC，‎ ‎∵点C为劣弧的中点，‎ ‎∴OC⊥BF，‎ ‎∵BF∥CE，∴OC⊥CE，‎ ‎∵OC是⊙O的半径，‎ ‎∴CE是⊙O的切线；‎ ‎(2)解：连接OF，交AC于点G，‎ ‎∵OA＝OC，∠BAC＝30°，‎ ‎∴∠BOC＝60°.‎ ‎∵点C为劣弧的中点，∴＝，‎ ‎∴∠FOC＝∠BOC＝60°，‎ ‎∵AB＝4，∴FO＝OC＝OB＝2.‎ ‎∵易证△AFG≌△COG，‎ ‎∴S阴影＝S扇形FOC＝＝π，‎ 即阴影部分的面积为π.‎ ‎23．(本小题满分12分)菱形ABCD的对角线AC，BD相交于点O，0°＜∠ABO≤60°，点G是射线OD上一个动点，过点G作GE∥DC交射线OC于点E，以OE，OG为邻边作矩形EOGF.‎ ‎(1)如图①，当点F在线段DC上时，求证：DF＝FC；‎ ‎(2)若延长AD与边GF交于点H，将△GDH沿直线AD翻折180°得到△MDH.‎ ‎①如图②，当点M在EG上时，求证：四边形EOGF为正方形；‎ ‎②如图③，当tan ∠ABO为定值m时，设DG＝k·DO，k为大于0的常数，当且仅当k＞2时，点M在矩形EOGF的外部，求m的值．‎ ‎(1)证明：∵四边形EOGF是矩形，‎ ‎∴EO∥GF，GO∥EF，‎ ‎∵GE∥DC，‎ ‎∴四边形GEFD是平行四边形，四边形GECF是平行四边形，‎ ‎∴GE＝DF，GE＝CF，‎ ‎∴DF＝FC.‎ ‎(2)①证明：如解图①，由折叠的性质知，∠GDH＝∠MDH，DH⊥GM.‎ ‎∵四边形ABCD是菱形，‎ ‎∴∠ADB＝∠BDC，‎ ‎∠COD＝90°，‎ ‎∵GE∥DC，‎ ‎∴∠BDC＝∠DGM.‎ ‎∵∠ADB＝∠GDH，‎ ‎∴∠DGM＝∠GDH，‎ ‎∵DH⊥GM，∴∠DGM＝45°，‎ ‎∴∠OEG＝45°，∴OE＝OG.‎ ‎∵四边形EOGF是矩形，‎ ‎∴四边形EOGF是正方形．‎ ‎②解：如解图②，‎ ‎∵四边形ABCD是菱形，‎ ‎∴∠ABD＝∠CBD＝∠ADB，‎ ‎∵GE∥CD，‎ ‎∴∠DGE＝∠CDB，‎ ‎∴∠ABD＝∠CBD＝∠ADB＝∠DGE＝∠CDB，‎ ‎∴∠GDM＝2∠ABD，‎ ‎∵tan ∠ABO＝m(m为定值)，‎ ‎∴点M始终在固定射线DM上并随k的增大向上运动，‎ ‎∵当且仅当k＞2时，M点在矩形EOGF的外部，‎ ‎∴k＝2时，M点在矩形EOGF上，即点M在EF上．‎ 设OB＝OD＝b，则OA＝OC＝mb，DG＝DM＝kb＝2b，OG＝(k＋‎ ‎1)b＝3b，OE＝m(k＋1)b＝3mb，GH＝HM＝mkb＝2mb，‎ ‎∴FH＝OE－GH＝3mb－2mb＝mb.‎ 过点D作DN⊥EF于点N，则DN＝OE＝3mb.‎ ‎∵∠FHM＋∠FMH＝∠FMH＋∠DMN＝90°，‎ ‎∴∠FHM＝∠DMN，‎ ‎∵∠F＝∠DNM＝90°，∴△MFH∽△DNM，‎ ‎∴＝，∴＝，‎ ‎∴MN＝b，‎ ‎∵DM2＝DN2＋MN2，‎ ‎∴(2b)2＝(3mb)2＋b2，‎ 解得m1＝，m2＝－(舍去)，‎ 故m＝.‎