青岛版四年级数学上路程、速度与时间的关系课件 25页

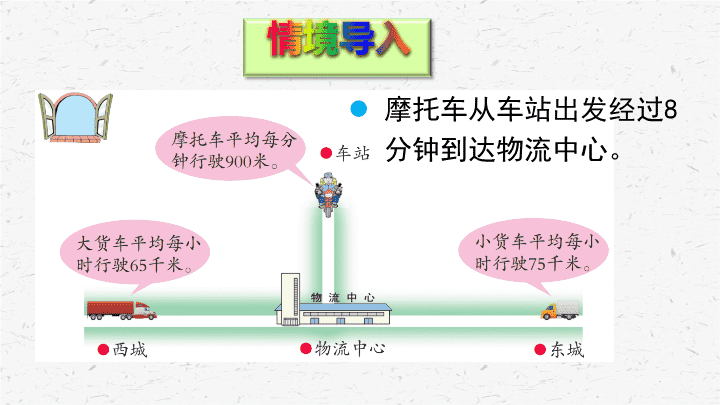
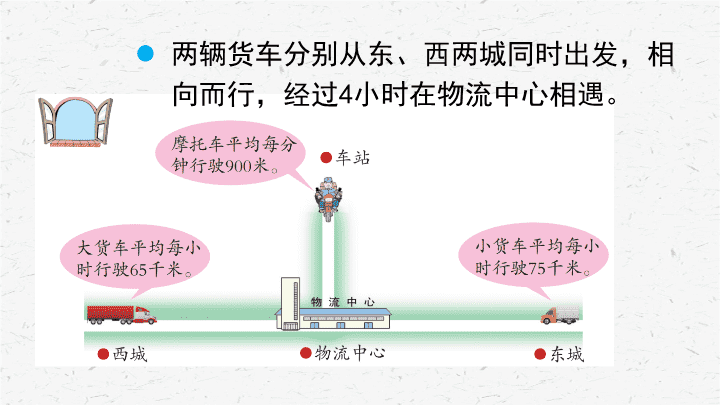
青岛版四年级上册 路程、速度与时间的关系 —— 解决问题 快捷的物流运输 六 情境导入 摩托车从车站出发经过 8 分钟到达物流中心。 两辆货车分别从东、西两城同时出发，相向而行，经过 4 小时在物流中心相遇。 从图中，你知道了哪些数学信息？ 根据这些信息，你能提出什么问题？ ？米 ？米 ？米 ？米 合作探究 车站与物流中心相距多少米？ 每分钟行驶的米数 行驶时间 车站与物流中心的距离 × = 7200 （米） 900 × 8 = 西城与物流中心相距多少千米？东城呢？ 西城与物流中心相距多少千米？东城呢？ 每小时行驶的千米数 行驶时间 西城与物流中心的距离 × = 260 （千米） 65 × 4 = 300 （千米） 75 × 4 = 每小时行驶的千米数 行驶时间 西城与物流中心的距离 × = 每分钟行驶的米数 行驶时间 车站与物流中心的距离 × = 速 度 路 程 “每分钟行驶 900 米”可以写作“ 900 米 / 分”，读作“ 900 米每分”。 你能说说速度、时间、路程之间的关系吗？ 摩托车平均每分钟行驶 900 米， 8 分钟能行驶 7200 米。 速度 × 时间 = 路程 900 米 / 分 × 8 分 = 7200 米　 摩托车 8 分钟行驶 7200 米，平均每分钟行驶 900 米。 7200 米 ÷ 8 分 = 900 米 / 分 路程 ÷ 时间 = 速度 从车站到物流中心的距离是 7200 米，摩托车平均每分钟行驶 900 米，需要 8 分钟到达。 7200 米 ÷ 900 米 / 分 = 8 分 路程 ÷ 速度 = 时间 路程、速度、时间 三者之间的关系是： 速度 × 时间 = 路程 路程 ÷ 时间 = 速度 路程 ÷ 速度 = 时间 知道其中的两个量，可以根据三者的关系求出第三个量。 东、西两城相距多少千米？ 求东、西两城相距多少千米，就是求两辆车行驶的总路程。 我们演示一下。 还可以画线段图整理条件和问题。 65 × 4 75 ×4 + = 260 + 300 = 560 （千米） 答：东、西两城相距 560 千米。 还可以画线段图整理条件和问题。 65+75 65+75 65+75 65+75 （ 65 + 75 ） × 4 = 140 × 4 = 560 （千米） 答：东、西两城相距 560 千米。 回顾上面两种解题思路，想一想，怎样解决相遇问题？ 自主练习 1. 先说说速度、时间和路程的关系，再填写下表。 595 15 3 2. 甲、乙两列火车分别从东、西两地同时相对开出， 5 小时后相遇。甲车速度是 110 千米 / 时，乙车速度是 100 千米 / 时。求东、西两地间的路程。（先画图整理条件和问题，再解答） 乙 甲 110 千米 100 千米 ？千米 （ 110 + 100 ） ×5 = 210 × 5 = 1050 （千米） 110 ×5 + 100×5 = 550 + 500 = 1050 （千米） 答：东、西两地相距 1050 千米。 3. （ 1 ）甲、乙两个工程队从同一地点分别向东、西两个方向铺设管道。甲队每天铺设管道 140 米，乙队每天铺设管道 150 米。 5 天后，两个工程队一共铺设管道多少米？（先画图整理条件和问题，再解答。） 西 甲每天铺设 140 米 东 乙每天铺设 150 米 ？米 （ 140 + 150 ） ×5 = 290 × 5 = 1450 （米） 140 ×5 + 150×5 = 700 + 750 = 1450 （米） 答：两个工程队一共铺设管道 1450 米。 （ 2 ）两队分别从两头同时施工， 8 个月开通。这条隧道长多少米？ （ 150 + 120 ） ×8 = 2160 （米） = 270 × 8 150×8 + 120×8 = 2160 （米） = 1200+960 答：这条隧道长 2160 米。 （ 3 ）两 人 同时开始录入一 份稿件 ， 1 小时正好录完。甲 的打字速度是 80 字 / 分，乙的打字速度是 65 字 / 分。 甲比 乙多录入多少个字？ 答：甲 1 小时比乙多录入 900 个字。 （ 80 - 65 ） ×60 = 900 （个） = 15 × 60 80×60 - 65×60 = 900 （个） = 4800 - 3900 想一想，上述 3 个问题与上面那些问题有着怎样的联系？ 数量关系和解题思路都与相遇问题基本一致。