五年级下册数学试题-奥数：立体图形的体积（解析版）全国通用 7页

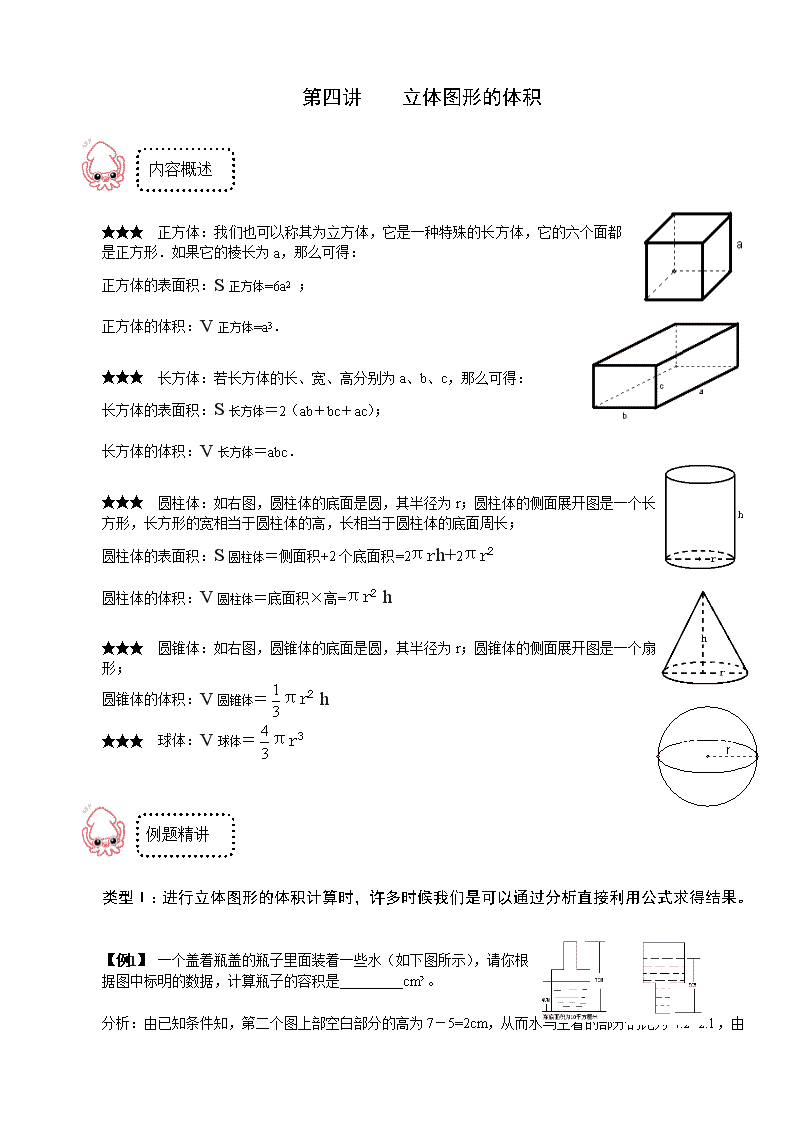
第四讲立体图形的体积内容概述★★★正方体：我们也可以称其为立方体，它是一种特殊的长方体，它的六个面都是正方形．如果它的棱长为a，那么可得：正方体的表面积：S正方体=6a2；正方体的体积：V正方体=a3．★★★长方体：若长方体的长、宽、高分别为a、b、c，那么可得：长方体的表面积：S长方体＝2（ab＋bc＋ac）；长方体的体积：V长方体＝abc．★★★圆柱体：如右图，圆柱体的底面是圆，其半径为r；圆柱体的侧面展开图是一个长方形，长方形的宽相当于圆柱体的高，长相当于圆柱体的底面周长；圆柱体的表面积：S圆柱体＝侧面积+2个底面积=2πrh+2πr2圆柱体的体积：V圆柱体＝底面积×高=πr2h★★★圆锥体：如右图，圆锥体的底面是圆，其半径为r；圆锥体的侧面展开图是一个扇形；圆锥体的体积：V圆锥体＝πr2h★★★球体：V球体＝πr3例题精讲类型Ⅰ：进行立体图形的体积计算时，许多时候我们是可以通过分析直接利用公式求得结果。【例1】一个盖着瓶盖的瓶子里面装着一些水（如下图所示），请你根据图中标明的数据，计算瓶子的容积是_________cm³。 分析：由已知条件知，第二个图上部空白部分的高为7－5=2cm，从而水与空着的部分的比为4:2=2:1，由图1知水的体积为10×4=40，所以总的容积为40÷2×（2+1）=60立方厘米。【例1】一个木盒从外面量长10厘米，宽8厘米，高5厘米，木板厚度1厘米，那么这个盒子的容积是多少立方厘米？分析：（10-2）×（8-2）×（5-2）=144（立方厘米）。【例2】有甲、乙两只圆柱形玻璃杯，其内直径依次是10厘米、20厘米，杯中盛有适量的水．甲杯中沉没着一铁块，当取出此铁块后，甲杯中的水位下降了2厘米；然后将铁块沉没于乙杯，且乙杯中的水未外溢．问：这时乙杯中的水位上升了多少厘米?分析：两个圆柱直径的比是l：2，所以底面面积的比是l：4．铁块在两个杯中排开的水的体积相同，所以乙杯中水升高的高度应当是甲杯中下降的高度的（注意此条件：乙杯中的水未外溢，如果溢出我们就不能这样计算了），即：2×=0．5(厘米)．注意运用比例解决问题。【例3】一个盛有水的圆柱形容器，底面内半径为5厘米，深20厘米，水深15厘米．今将一个底面半径为2厘米，高为17厘米的铁圆柱垂直放人容器中．求这时容器的水深是多少厘米?分析：法1：若圆柱体部分浸入水中，则水深为：，17.86大于铁圆柱得高度17，这与我们得假设不符，所以圆柱体完全浸入水中，那么参看法2的解法即得答案。法2：若圆柱体能完全浸入水中，则水深与容器底面面积的乘积应等于原有水的体积与圆柱体在水中体积之和，因而水深为：=17.72(厘米)．它比圆柱体的高度要大，可见圆柱体可以完全浸入水中，而且小于20厘米，显然水也未溢出．于是所求的水深便是17．72厘米．在这个题目中存在一个判断圆柱体是被水完全浸没，还是部分被浸没，以及水是否溢出的过程，请教师注意引导学生。【例4】如图，在一个立方体的两对侧面的中心各打通一个长方体的洞在上下侧面的中心打通一个圆柱形的洞，已知立方体边长为10厘米，侧面上的洞口是边长为4厘米的正方形，上下侧面的洞口是直径为4厘米的圆，求该立方体的体积(取=3)．分析：体积为：一2××10+-××（10-4）=672(立方厘米)．【例5】在底面是边长为60厘米的正方形的一个长方体容器里，直立着一个高100厘米，底面为边长15厘米的正方形的四棱柱铁棍，这时容器里的水深50厘米。现在把铁棍轻轻地向正上方提起24厘米，露出水面的四棱柱铁棍浸湿部分长多少厘米？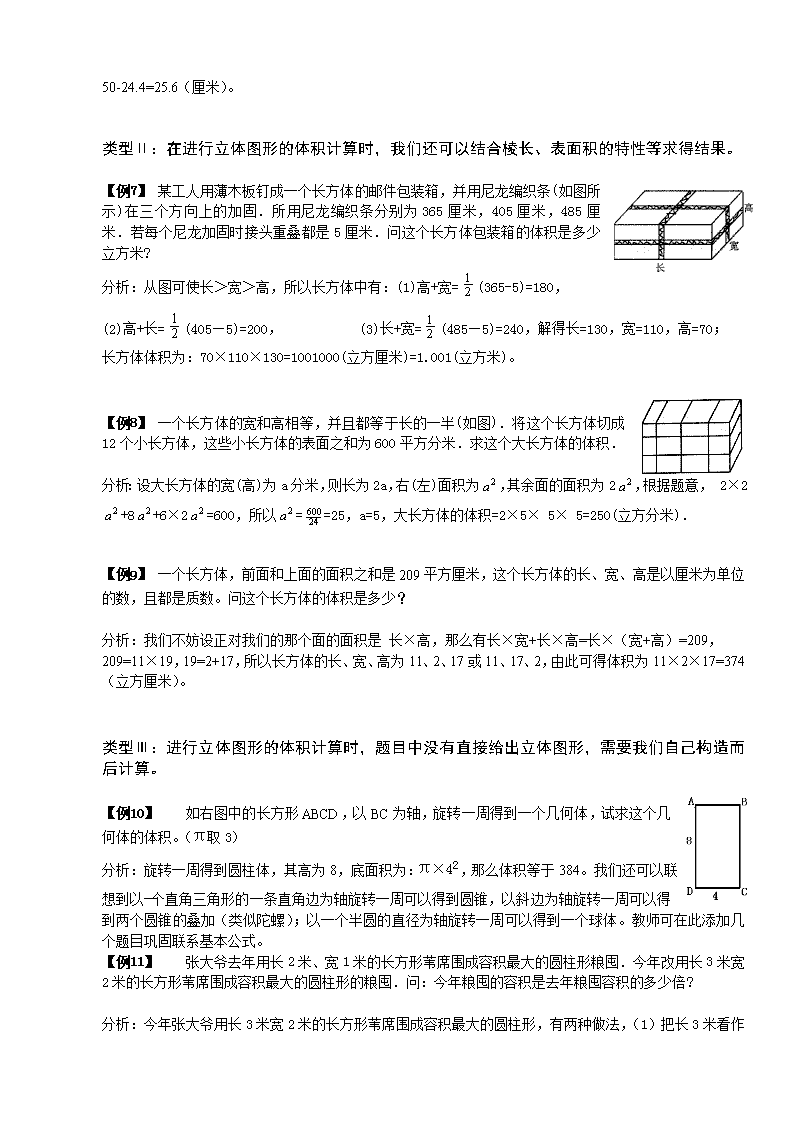分析：容器里的水共有（60×60-15×15）×50，当把铁棍提起24厘米时，铁棍仍浸湿在水中的部分长是：[（60×60-15×15）×50-60×60×24]÷（60×60-15×15 ）=24.4（厘米），所以露出水面的浸湿部分长是：50-24.4=25.6（厘米）。类型Ⅱ：在进行立体图形的体积计算时，我们还可以结合棱长、表面积的特性等求得结果。【例1】某工人用薄木板钉成一个长方体的邮件包装箱，并用尼龙编织条(如图所示)在三个方向上的加固．所用尼龙编织条分别为365厘米，405厘米，485厘米．若每个尼龙加固时接头重叠都是5厘米．问这个长方体包装箱的体积是多少立方米?分析：从图可使长＞宽＞高，所以长方体中有：(1)高+宽=(365-5)=180，(2)高+长=(405—5)=200，(3)长+宽=(485—5)=240，解得长=130，宽=110，高=70；长方体体积为：70×110×130=1001000(立方厘米)=1.001(立方米)。【例2】一个长方体的宽和高相等，并且都等于长的一半(如图)．将这个长方体切成12个小长方体，这些小长方体的表面之和为600平方分米．求这个大长方体的体积．分析：设大长方体的宽(高)为a分米，则长为2a，右(左)面积为，其余面的面积为2，根据题意，2×2+8+6×2=600，所以==25，a=5，大长方体的体积=2×5×5×5=250(立方分米)．【例3】一个长方体，前面和上面的面积之和是209平方厘米，这个长方体的长、宽、高是以厘米为单位的数，且都是质数。问这个长方体的体积是多少？分析：我们不妨设正对我们的那个面的面积是长×高，那么有长×宽+长×高=长×（宽+高）=209，209=11×19，19=2+17，所以长方体的长、宽、高为11、2、17或11、17、2，由此可得体积为11×2×17=374（立方厘米）。类型Ⅲ：进行立体图形的体积计算时，题目中没有直接给出立体图形，需要我们自己构造而后计算。【例4】如右图中的长方形ABCD，以BC为轴，旋转一周得到一个几何体，试求这个几何体的体积。（π取3）分析：旋转一周得到圆柱体，其高为8，底面积为：π×42，那么体积等于384。我们还可以联想到以一个直角三角形的一条直角边为轴旋转一周可以得到圆锥，以斜边为轴旋转一周可以得到两个圆锥的叠加（类似陀螺）；以一个半圆的直径为轴旋转一周可以得到一个球体。教师可在此添加几个题目巩固联系基本公式。【例5】张大爷去年用长2米、宽1米的长方形苇席围成容积最大的圆柱形粮囤．今年改用长3米宽2米的长方形苇席围成容积最大的圆柱形的粮囤．问：今年粮囤的容积是去年粮囤容积的多少倍?分析：今年张大爷用长3米宽2米的长方形苇席围成容积最大的圆柱形，有两种做法，（1）把长3米 看作底面周长，那么宽2看作圆柱的高；（2）把宽2米看作底面周长，那么长3看作圆柱的高；比较可得（1）种方法所得体积较大，依此计算，底面周长是3，半径是，，所以今年粮囤底面积是，高是2；同理，去年粮囤底面积是，高是1．今年粮囤容积是去年粮囤容积的：【例1】现有一张长40厘米、宽20厘米的长方形铁皮，请你用它做一只深是5厘米的长方体无盖铁皮盒(焊接处及铁皮厚度不计，容积越大越好)，你做出的铁皮盒容积是多少立方厘米?分析：法1：探讨分析比较得到答案。（1）如右图，在40×20的长方形铁皮的四角截去边长5厘米的正方形铁皮，然后焊接成长方形无盖铁皮盒．这个铁皮盒的：长=40-5-5=30(厘米)，宽=20-5-5=10(厘米)，高=5(厘米)，体积=30×10×5=1500(立方厘米)．（2）如右图，在40×20长方形铁皮的左侧两角上割下边长5厘米的正方形(二块)，紧密焊接到右侧的中间部分，这样做成的无盖铁皮盒的长=40—5=35(厘米)，宽=20—5—5=10(厘米)，高=5(厘米)，体积=35×10×5=1750(立方厘米)．（3）如右图，在40×20的长方形铁皮的左右两侧各割下一条宽为5厘米的长方形铁皮(共二块)，分别焊到上、下的中间部分，这样做成的无盖铁皮盒的长=40-5-5-5-5=20(厘米)，宽=20(厘米)，高=5(厘米)，体积=20×20×5=2000(立方厘米)．因此，最后一种容积最大．法2：你要想使容积最大，就要充分利用手中的铁皮，如果能将铁皮都用上那么就能得到一个最大的铁盒。如下图（1），我们从原铁皮上切割下4块5×20的长方体，如图（2），将其焊接上能做成一只深是5厘米的长方体无盖铁皮盒，那么此时的容积最大：20×20×5=2000(立方厘米)．附加题目 【附1】如下面图1那样,在用塑料制的三棱柱形的筒里装着水,这个筒的展开图如下面图2.现在,如图1那样,把这个筒的面作为底面,放在水平的桌面上,水面高度是2.按上面讲的条件回答下列问题:(1)把面作为底面,放在水平的桌面上,水面高多少厘米?(2)把面(直角三角形的面)作为底面,放在水平的桌面上,水面高又是多少厘米?分析：以面作为底面时，水的体积为：（3+3/2）×2÷2×12=54（立方厘米）。（1）把面作为底面时,由于以A为底面时，有水的部分占其纵横面（底边为3厘米的三角形）面积的3/4，而以B为底面时，纵截面与上述纵截面相同，故以4厘米的边为底边，有水部分仍占其面积的3/4，因此水面高度为截面三角形高度的一半，即为1.5厘米；（2）以C面为底面时。水的高度为：54÷（1/2×3×4）=9（厘米）。【附2】用直径为20厘米的圆柱形钢材，锻造长300厘米，宽100厘米，厚5厘米的长方形钢板，应截取圆柱形钢材多长？（π取3）分析：500厘米。【附3】一个底面为正方形的长方体木块被锯掉一部分，变成如右图所示的六面体ABCD-EFGH，其中最长的边DH=8厘米，最短的边AB=BC=CD=DA=BF=4厘米，那么这个六面体的体积是多少立方厘米？分析：42．这个六面体的体积是长4厘米，宽4厘米，高12厘米的长方体体积的一半，即4×4×12÷2=96(立方厘米).【附4】某工厂原用长4米、宽1米的铁皮围成没有底和顶的正方体形状的产品存放处(底和顶另用别的材料)，恰好够存放一周的产品．现在产量增加了27％，问：能否还用原来的铁皮围成存放处，装下现在一周的产品?分析：将此铁皮沿长4米的边卷起成圆柱面．圆柱底面的圆周长为4米，因而半径为．由于高为l米，圆柱体积为：V=××1==≈1.274(立方米)．现在(圆柱)的体积和原来(正方体)的体积之比是：≈1.274=127．4％，即体积增加了127．4％一100％=27．4％．现在产量增加了27％，仍能装下。【附5】（第八届迎春杯数学竞赛决赛）一个长、宽、高分别为21厘米、15厘米、12厘米的长方体．现从它的上面尽可能大的切下一个正方体．然后从剩余的部分再尽可能大的切下一个正方体．最后再从第二次剩余的部分尽可能大的切下一个正方体．剩下的体积是多少平方厘米？分析：本题的关键在于确定三次切下的正方体的棱长．由于21：15：12= 7：5：4，为方便起见．我们先考虑长、宽、高分别为7厘米、5厘米、4厘米的长方体．因为7>5>4，容易知道第一次切下的正方体棱长应该是4厘米(如图)．第二次切时，切下棱长为3厘米的正方体符合要求.第三次切时，切下棱长为2厘米的正方体符合要求．剩下的体积应是：21×15×12一(++)=1107(平方厘米)．这个题目的思路我们可以参看附7。【附6】如右图，是一个长方形铁皮，利用图中的阴影部分，刚好能做成一个油桶（接头处忽略不计），求这个油桶的容积。（π取3.14）分析：圆的直径为：16.56÷（1+3.14）=4（m），而油桶的高为2个直径长，即为：4×2=8（m），故体积为100.48立方米。练习四1．一个长方体的各条棱长的和是48厘米，并且它的长是宽的2倍，高与宽相等，那么这个长方体的体积是______立方厘米．解答：依题意，这个长方体的长、宽、高之和是48÷4=12(厘米)，于是它的宽与高都等于12÷(2+1+1)=3(厘米)，它的长是3×2=6厘米．所以这个长方体的体积是6×3×3=54(立方厘米)．2．如右图，有一个圆柱和一个圆锥，它们的高和底面直径都标在图上，单位是厘米．那么，圆锥体积与圆柱体积的比是多少?解答：圆锥的体积是，圆柱的体积是．所以，圆锥体积与圆柱体积的比是.3．在棱长为3cm的正方体木块的每个面的中心上打一个直穿木块的洞，洞口呈边长为1cm的正方形（见右图）。求挖洞后木块的体积。解答：33-12×3×3+2×13=20cm3。4．如图，从长为13厘米，宽为9厘米的长方形硬纸板的四角去掉边长为2厘米的正方形，然后沿虚线折叠成长方体容器．这个容器的体积是多少立方厘米?解答：容器的底面积是：(13—4)×(9—4)=45(平方厘米)，高为2厘米，所以容器的体积是：45×2=90(立方厘米)．5．一个圆柱形玻璃杯内盛有水，水面高2．5厘米，玻璃杯内侧的底面积是72平方厘米．在这个杯中放进棱长6厘米的正方体铁块后，水面没有淹没铁块．这时水面高多少厘米?解答：把放入铁块后的玻璃杯看作一个底面如右图的新容器，底面积是： 72—6×6=36(平方厘米)，水的体积是：72×2．5=180(立方厘米)，后来水面的高为：180÷36=5(厘米)．6．用一块长30厘米，宽20厘米的长方形铁皮做圆柱形容器的侧面，再用另一块铁皮做底，问怎样做才能使这个圆柱形容器的容积为最大?7．一个长方体木块，从下部和上部分别截去高为3厘米和2厘米的长方体后，便成为一个正方体，表面积减少了120平方厘米，原来长方体的体积是立方厘米．解答：所成立方体的棱长为：120÷(3+2)÷4=6(厘米)，所以原长方体的体积为：6×6×(6+3+2)=396(立方厘米)。课外知识小猴摘果数学兴趣课上，刘老师给同学们出了这样一道有趣的儿歌型应用题：　　三百七十八个果，小猴边摘边唱歌，　　开始一天真快乐，逐日少摘一半果，　　转眼六天匆匆过，每天摘果多少个？　　同学们读完题后，觉得很有趣，便在草稿纸上算了起来。　　一会儿，李小林同学举手发言，他说：我们可以这样来思考：小猴要摘的果子一共是378个，用去的时间一共是6天。6天中，一天比一天少摘一半的果子，因此，可把最后一天摘的果子数看作1份，这样倒推就知，第五、四、三、二、一天各摘的果子就是2、4、8、16、32份。先求出总份数：1＋2＋4＋8＋16＋32=63(份）。所以，第六天摘的果子是：378÷63=6（个）；第五天摘：6×2=12（个）；第四天摘：6×4=24（个）；第三天摘：6×8=48（个）；第二天摘：6×16=96（个）；第一天摘：6×32=192（个）。　　听了李小林同学的发言，刘老师微笑着点了点头，并表扬李小林是一个爱动脑筋的好学生。小朋友，你还会用别的方法解答吗？