2019-2020学年人教版五年级（下）期中数学试卷 20页

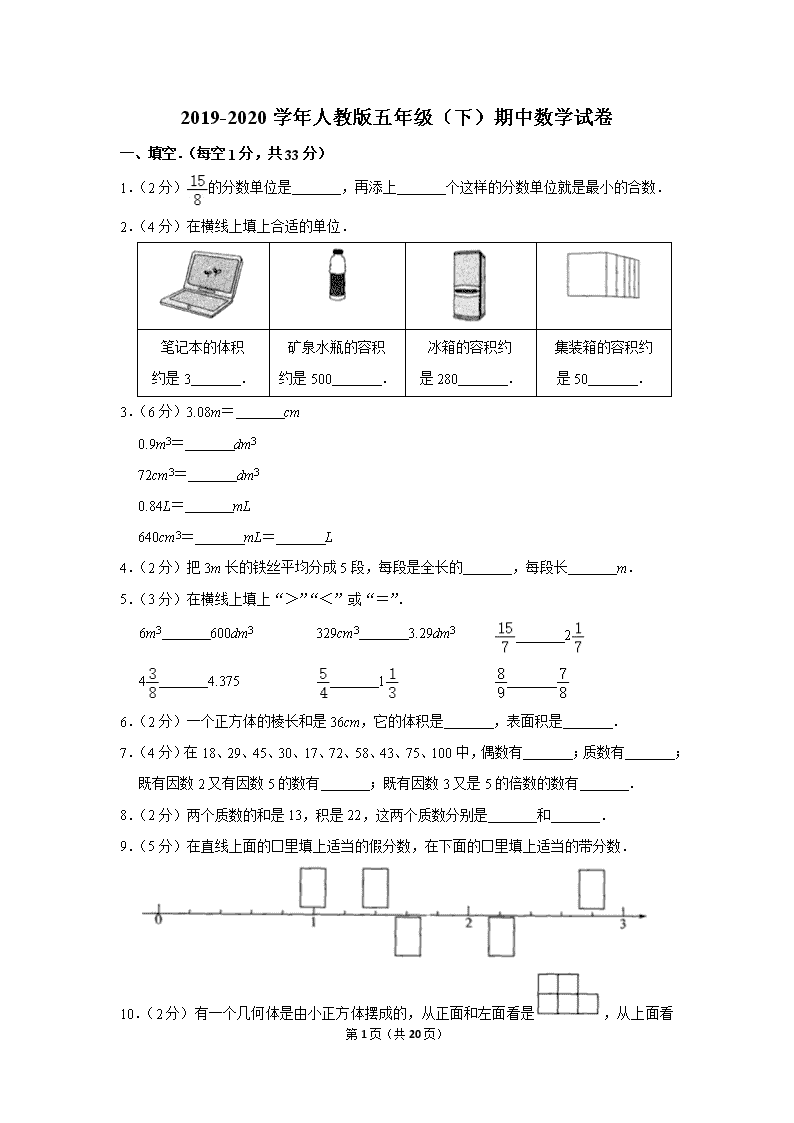
‎2019-2020学年人教版五年级（下）期中数学试卷 一、填空．（每空1分，共33分）‎ ‎1．（2分）的分数单位是　 　，再添上　 　个这样的分数单位就是最小的合数．‎ ‎2．（4分）在横线上填上合适的单位．‎ 笔记本的体积 约是3　 　．‎ 矿泉水瓶的容积 约是500　 　．‎ 冰箱的容积约 是280　 　．‎ 集装箱的容积约 是50　 　．‎ ‎3．（6分）3.08m＝　 　cm ‎0.9m3＝　 　dm3‎ ‎72cm3＝　 　dm3‎ ‎0.84L＝　 　mL ‎640cm3＝　 　mL＝　 　L ‎4．（2分）把3m长的铁丝平均分成5段，每段是全长的　 　，每段长　 　m．‎ ‎5．（3分）在横线上填上“＞”“＜”或“＝”．‎ ‎6m3　 　600dm3‎ ‎329cm3　 　3.29dm3‎ ‎　 　2‎ ‎4　 　4.375‎ ‎　 　1‎ ‎　 　‎ ‎6．（2分）一个正方体的棱长和是36cm，它的体积是　 　，表面积是　 　．‎ ‎7．（4分）在18、29、45、30、17、72、58、43、75、100中，偶数有　 　；质数有　 　；既有因数2又有因数5的数有　 　；既有因数3又是5的倍数的数有　 　．‎ ‎8．（2分）两个质数的和是13，积是22，这两个质数分别是　 　和　 　．‎ ‎9．（5分）在直线上面的□里填上适当的假分数，在下面的□里填上适当的带分数．‎ ‎10．（2分）有一个几何体是由小正方体摆成的，从正面和左面看是 第20页（共20页）‎ ‎，从上面看是，这个几何体至少是由　 　个小正方体摆成的，最多是由　 　个小正方体摆成的．‎ ‎11．（1分）一个正方体和一个长方体拼在一起成为一个新的长方体，新的长方体的表面积比原来长方体的表面积增加64cm2．正方体的表面积是　 　平方厘米．‎ 二、判断．（对的画“√”，错的画“×”。5分，每题1分）‎ ‎12．（1分）根据从一个方向看到的图形摆小正方体，只有一种摆法．　 　（判断对错）‎ ‎13．（1分）把5千克水泥平均分成8份，每份重千克．　 　（判断对错）‎ ‎14．（1分）假分数都不是最简分数．　 　．（判断对错）‎ ‎15．（1分）两个不同的非0自然数的最小公倍数一定比他们的最大公因数大．　 　（判断对错）‎ ‎16．（1分）一个长方体至少有四个面是长方形．　 　．（判断对错）‎ 三、选择．（把正确答案的序号填在括号里）（6分，每题1分）‎ ‎17．（1分）的分子减少6，要使分数的大小不变，分母应该（　　）‎ A．减少6 B．减少8 C．减少9‎ ‎18．（1分）已知三位数“4□1”正好是三个连续自然数的和，□里的数字可能是（　　）‎ A．3 B．4 C．5‎ ‎19．（1分）用两根长度相等的铁丝分别围成一个正方体和一个长方体框架，它们的表面积相比，（　　）‎ A．长方体的大 B．正方体的大 ‎ C．无法判断谁大 ‎20．（1分）两个数的最大公因数是4，最小公倍数是24，这两个数不可能是（　　）‎ A．4和24 B．8和12 C．8和24‎ ‎21．（1分）下面的平面图中，（　　）号不能折成正方体．‎ 第20页（共20页）‎ A． B． ‎ C．‎ ‎22．（1分）在下面的几何体中，从正面看到的图形相同的有（　　）个．‎ A．2 B．3 C．4‎ 四、按要求完成下面各题．（23分）‎ ‎23．（12分）写出每组数的最大公因数和最小公倍数．‎ ‎（1）12和60‎ 最大公因数是　 　．‎ 最小公倍数是　 　．‎ ‎（2）13和14‎ 最大公因数是　 　．‎ 最小公倍数是　 　．‎ ‎（3）26和65‎ 最大公因数是　 　．‎ 最小公倍数是　 　．‎ ‎24．（3分）把下列各数按从小到大的顺序排列．‎ ‎、1.2、、0.45、1、．　 　‎ ‎25．（8分）计算如图图形的表面积和体积．（单位：cm）‎ 五、解决问题．（33分）‎ 第20页（共20页）‎ ‎26．（4分）48名女生和72名男生排成队列进行表演，要使女生队列和男生队列每列人数相等，那么每列最多有多少人？一共有几列？‎ ‎27．（4分）甲、乙两人暑假去图书馆看书，甲每4天去一次，乙每5天去一次．如果6月27日他们在图书馆相遇，那么他们下一次在图书馆相遇是几月几日？‎ ‎28．（4分）同学们采集树种，第一组10人采集了8kg，第二组12人采集了10kg，第三组14人采集了12kg．哪一组平均每人采集得最多？‎ ‎29．（8分）游乐中心的游泳池是一个长方体，长50m，宽25m，高2m．‎ ‎（1）如果在游泳池内注入1.6m深的水，那么注入的水有多少立方米？‎ ‎（2）如果在这个游泳池的四周及底面贴上瓷砖，要用多少平方米的瓷砖？‎ ‎30．（5分）在一个长10dm、宽6dm、高4dm的长方体玻璃水缸中，倒入3dm深的水，然后放入一个棱长4dm的正方体钢块，水缸里溢出多少升的水？‎ ‎31．（8分）如图，一根方钢长6m，横截面是一个边长4cm的正方形．‎ ‎（1）这根方钢重多少千克？（1cm3钢重7.8g）‎ ‎（2）一辆载质量5t的货车能否一次运载50根这样的方钢？‎ 第20页（共20页）‎ ‎2019-2020学年人教版五年级（下）期中数学试卷 参考答案与试题解析 一、填空．（每空1分，共33分）‎ ‎1．（2分）的分数单位是　　，再添上　17　个这样的分数单位就是最小的合数．‎ ‎【分析】（1）一个分数的分数单位看分母，分母是几，分数单位就是几分之一，分子是几，它就含有几个这样的单位．‎ ‎（2）最小的合数是4，用4减去原分数的结果，再看有几个分数单位即可解答．‎ ‎【解答】解：的分数单位是．‎ ‎4﹣＝．即再添上 17个这样的分数单位就是最小的合数．‎ 故答案为：；17．‎ ‎【点评】此题主要考查分数的单位：把单位“1”平均分成几份，表示其中一份的数就是它的分数单位；也考查了最小的合数是4．‎ ‎2．（4分）在横线上填上合适的单位．‎ 笔记本的体积 约是3　立方分米　．‎ 矿泉水瓶的容积 约是500　毫升　．‎ 冰箱的容积约 是280　升　．‎ 集装箱的容积约 是50　立方米　．‎ ‎【分析】根据生活经验、对体积和容积单位大小的认识和数据的大小，选择合适的单位填空，即可得解．‎ ‎【解答】解：‎ 笔记本的体积 约是3立方分米．‎ 矿泉水瓶的容积 约是500毫升．‎ 冰箱的容积约 是280升．‎ 集装箱的容积约 是50立方米．‎ 故答案为：立方分米；毫升；升；立方米．‎ 第20页（共20页）‎ ‎【点评】此题考查根据情景选择合适的计量单位，要注意联系生活实际、计量单位和数据的大小，灵活的选择．‎ ‎3．（6分）3.08m＝　308　cm ‎0.9m3＝　900　dm3‎ ‎72cm3＝　0.072　dm3‎ ‎0.84L＝　840　mL ‎640cm3＝　640　mL＝　0.64　L ‎【分析】把3.08米化成厘米数，用3.08乘进率100；‎ 把0.9立方米化成立方分米数，用0.9乘进率1000；‎ 把72立方厘米化成立方分米数，用72除以进率1000；‎ 把0.84升化成毫升数，用0.84乘进率1000；‎ 把640立方厘米化成毫升数，数不变，化成升数，用640除以进率1000；即可得解．‎ ‎【解答】解：3.08m＝308cm ‎0.9m3＝900dm3‎ ‎72cm3＝0.072dm3‎ ‎0.84L＝840mL ‎640cm3＝640mL＝0.64L 故答案为：308，900，0.072，840，640，0.64．‎ ‎【点评】此题考查名数的换算，把高级单位的名数换算成低级单位的名数，就乘单位间的进率；把低级单位的名数换算成高级单位的名数，就除以单位间的进率．‎ ‎4．（2分）把3m长的铁丝平均分成5段，每段是全长的　　，每段长　　m．‎ ‎【分析】把3米长的铁丝平均分成5段，根据分数的意义可知，即将这根铁丝全长当做单位“1”平均分成5段，则每段是全长的1÷5＝，每段的长为3×＝米．‎ ‎【解答】解：每段是全长的1÷5＝，‎ 每段的长为3×＝（米）；‎ 故答案为：，．‎ ‎【点评】本题主要考查了学生对于分数意义的理解：将单位“1”平均分成若干份，表示其中这样一份或几份的数为分数．‎ 第20页（共20页）‎ ‎5．（3分）在横线上填上“＞”“＜”或“＝”．‎ ‎6m3　＞　600dm3‎ ‎329cm3　＜　3.29dm3‎ ‎　＝　2‎ ‎4　＝　4.375‎ ‎　＜　1‎ ‎　＞　‎ ‎【分析】（1）6立方米＝6000立方分米，6000立方分米＞600立方分米．‎ ‎（2）329立方厘米＝0.329立方分米，0.329立方分米＜3.29立方分米．‎ ‎（3）把假分数化成带分数或把带分数化成假分数再比较．‎ ‎（4）把4化成小数再比较．‎ ‎（5）把化成假分数是1，两个带分数整数部分相同，分数部分分子相同，分母大的反而小．‎ ‎（6）把这两个分数先通分化成分母相同的分数，再根据相同分母的分数大小比较方法进行比较．‎ ‎【解答】解：‎ ‎（1）6m＞600dm3‎ ‎（2）329cm＜3.29dm3‎ ‎ （3）＝2‎ ‎（4）4＝4.375‎ ‎（5）＜1‎ ‎（6）＞‎ 故答案为：＞，＜，＝，＝，＜，＞．‎ ‎【点评】不同单位的名数的大小比较通常是先化成相同的单位名数，再根据数值的大小进行比较．对于分母或分子相同的分数，可根据同分母或同分子分数比较大小的方法进行比较；对于分母和分子都不相同的分数，通常是采用先通分再比较大小的方法．整数部分不同的带分数，整数部分大的带分数就比较大．‎ ‎6．（2分）一个正方体的棱长和是36cm，它的体积是　27立方厘米　，表面积是　54平方厘米　．‎ ‎【分析】首先用棱长总和除以12求出棱长，再根据正方体的体积公式：V＝a3　表面积公式：S＝6a2解答即可．‎ ‎【解答】解：36÷12＝3（厘米）‎ ‎3×3×3＝27（立方厘米）‎ ‎3×3×6＝54（平方厘米）‎ 答：它的体积是27立方厘米，表面积是54平方厘米．‎ 第20页（共20页）‎ 故答案为：27立方厘米、54平方厘米．‎ ‎【点评】此题主要考查正方体的棱长总和公式、体积公式、表面积公式的灵活运用，关键是熟记公式．‎ ‎7．（4分）在18、29、45、30、17、72、58、43、75、100中，偶数有　18、30、72、58、100　；质数有　29、17、43　；既有因数2又有因数5的数有　30、100　；既有因数3又是5的倍数的数有　45、30、75　．‎ ‎【分析】根据偶数、奇数，质数、合数的意义，是2的倍数的数叫做偶数，又叫做双数，不是2的倍数的数叫做奇数，又叫做单数；一个自然数，如果只有1和它本身两个因数，这样的数叫做质数；一个自然数，如果除了1和它本身还有别的因数，这样的数叫做合数，解答即可．‎ 根据2、3、5的倍数的特征：个位上是0、2、4、6、8的数都是2的倍数；各位上的数字之和是3的倍数，这个数一定是3的倍数；个位上是0或5的数都是5的倍数；‎ ‎【解答】解：根据题意得：‎ 在18、29、45、30、17、72、58、43、75、100中，‎ 偶数有：18、30、72、58、100；‎ 质数有：29、17、43．‎ ‎2的倍数有 18、30、72、58、100；‎ ‎3的倍数有10、45、30、72、75；‎ ‎5的倍数有45、30、75、100，‎ 既有因数2又有因数5的数有30、100，‎ 既有因数3又是5的倍数的数有45、30、75．‎ 故答案为：18、30、72、58、100；29、17、43；30、100；45、30、75．‎ ‎【点评】此题考查了质数、偶数的意义，2、3、5的倍数的特征．解题的关键是掌握质数、偶数的意义，2、3、5的倍数特征，能够灵活运用．‎ ‎8．（2分）两个质数的和是13，积是22，这两个质数分别是　2　和　11　．‎ ‎【分析】因为两个质数的乘积是22，把22分解质因数即可解决此题．‎ ‎【解答】解：因为22＝2×11，‎ 又符合2+11＝13，‎ 所以这两个质数是2和11，‎ 故答案为：2、11．‎ 第20页（共20页）‎ ‎【点评】此题考查根据两个质数的和与积，推算两个质数是多少，只要把乘积分解质因数即可解决问题．‎ ‎9．（5分）在直线上面的□里填上适当的假分数，在下面的□里填上适当的带分数．‎ ‎【分析】把数轴上一个单位长看作单位“1”，把它平均分成5份，每份表示，用真分数或假分数表示时，这样的几份就是五分之几；用带分数表示时，在整数几的后面，整数部分就是几，要表示的这样的几份，就是五分之几，合起来就是几又五分之几．‎ ‎【解答】解：‎ ‎【点评】此题是考查分数的意义．把单位“1”平均分成若干份，用分数表示，分母是分成的份数，分子是要表示的份数．‎ ‎10．（2分）有一个几何体是由小正方体摆成的，从正面和左面看是，从上面看是，这个几何体至少是由　8　个小正方体摆成的，最多是由　10　个小正方体摆成的．‎ ‎【分析】根据从正面、左面和上面看到的形状，摆成这个立体图形最少需要8个相同的小正方体，最多需要10个相同的小正方体．最少8个时，后排下层3个，上层居中1个；中排下层2个，上层1个，左齐；前排1个，三排左齐；最多10个时，在后排的左边、中排右边上面各摆1个．‎ ‎【解答】解：有一个几何体是由小正方体摆成的，从正面和左面看是 第20页（共20页）‎ ‎，从上面看是，这个几何体的形状如下：‎ 这个几何体至少是由8个小正方体摆成的，最多是由10个小正方体摆成的．‎ 故答案为：8，10．‎ ‎【点评】本题是考查作简单图形的三视图，能正确辨认从正面、上面、左面（或右面）观察到的简单几何体的平面图形．此类题可找些小正方体亲自摆一下，既锻炼了动手操作能力，又能决问题．‎ ‎11．（1分）一个正方体和一个长方体拼在一起成为一个新的长方体，新的长方体的表面积比原来长方体的表面积增加64cm2．正方体的表面积是　96　平方厘米．‎ ‎【分析】一个正方体和一个长方体拼在一起拼成了一个新的长方体，那么表面积比原来长方体实际是增加了4个小正方体的面，可以求出每个小正方体面的面积是：64÷4＝16平方厘米，由此可得小正方体的棱长是4厘米，再利用正方体的表面积公式解答即可．‎ ‎【解答】解：64÷4＝16（平方厘米），‎ 因为4×4＝16，所以小正方体的棱长是4厘米，‎ 则正方体的表面积是：4×4×6＝96（平方厘米），‎ 答：正方体的表面积是96平方厘米．‎ 故答案为；96．‎ ‎【点评】此题的关键是：根据正方体和长方体的拼组特点，得出表面积增加的64平方厘米是这个正方体的4个面的面积，从而求出正方体的棱长解答问题．‎ 二、判断．（对的画“√”，错的画“×”。5分，每题1分）‎ ‎12．（1分）根据从一个方向看到的图形摆小正方体，只有一种摆法．　×　（判断对错）‎ ‎【分析】根据从一个方向看到的图形摆小正方体，不能确定这个物体的形状，有很多种摆法，根据从三个方向看到的图形才能确定物体的形状，据此即可解答问题．‎ 第20页（共20页）‎ ‎【解答】解：根据题干分析可得，根据从一个方向看到的图形摆小正方体，不能确定这个物体的形状，有很多种摆法，‎ 原题说法错误．‎ 故答案为：×．‎ ‎【点评】此题考查了从不同方向观察几何体，锻炼了学生的空间想象力和抽象思维能力．‎ ‎13．（1分）把5千克水泥平均分成8份，每份重千克．　正确　（判断对错）‎ ‎【分析】根据除法的意义，用5千克除以8即可．‎ ‎【解答】解：5÷8＝（千克）；‎ 故答案为：正确．‎ ‎【点评】每份的重量是个具体的数量，后面要带单位，每份是单位“1”的几分之几，不需要带单位．‎ ‎14．（1分）假分数都不是最简分数．　错误　．（判断对错）‎ ‎【分析】最简分数的意义：分子分母是互质数的分数就是最简分数．所以最简分数的分子分母只要是互质数就可以，据此可知：假分数只要分子分母是互质数就是最简分数，可以举例证明，据此解答．‎ ‎【解答】解；、都是假分数，也都是最简分数，所以假分数都不是最简分数的说法是错误的；‎ 故答案为；错误．‎ ‎【点评】本题主要考查最简分数的意义．注意只要分子分母是互质数就是最简分数．‎ ‎15．（1分）两个不同的非0自然数的最小公倍数一定比他们的最大公因数大．　√　（判断对错）‎ ‎【分析】两个不同的非0自然数的最小公倍数，最小的时候是这两个数中最大的那个数；最大公因数，最大的时候是这两个数中最小的那个数；所以，两个不同的非0自然数的最小公倍数一定比他们的最大公因数大；进而得出结论．‎ ‎【解答】解：两个不同的非0自然数的最小公倍数，最小的时候是这两个数中最大的那个数；最大公因数，最大的时候是这两个数中最小的那个数；‎ 所以，两个不同的非0自然数的最小公倍数一定比他们的最大公因数大是正确的．‎ 故答案为：√．‎ 第20页（共20页）‎ ‎【点评】解答此题应结合题意，根据两个数的最大公因数和最小公倍数的关系进行解答．‎ ‎16．（1分）一个长方体至少有四个面是长方形．　√　．（判断对错）‎ ‎【分析】根据长方体的特征，长方体的6个面都是长方形（特殊情况下有两个相对的面是正方形），由此解答．‎ ‎【解答】解：长方体的6个面都是长方形（特殊情况下有两个相对的面是正方形），因此，一个长方体至少有4个面是长方形．‎ 故答案为：√．‎ ‎【点评】此题主要考查长方体的特征，特别是考查长方体面的特征．‎ 三、选择．（把正确答案的序号填在括号里）（6分，每题1分）‎ ‎17．（1分）的分子减少6，要使分数的大小不变，分母应该（　　）‎ A．减少6 B．减少8 C．减少9‎ ‎【分析】的分子减少6，即分子变为9﹣6＝3，9÷3＝3，分子缩小了3倍，根据分数的基本性质，要使分数大小不变，分母也应缩小3倍，12÷3＝4＝12﹣8．‎ ‎【解答】解：9﹣6＝3，9÷3＝3，分子缩小了3倍，‎ 要使分数大小不变，分母也应缩小3倍，‎ 即12÷3＝4＝12﹣8．‎ 故选：B．‎ ‎【点评】本题考查了学生根据分数的基本性质解决问题的能力．‎ ‎18．（1分）已知三位数“4□1”正好是三个连续自然数的和，□里的数字可能是（　　）‎ A．3 B．4 C．5‎ ‎【分析】4□1是连续三个自然数的和，意味着平均值是中间的哪个数，也意味着4□1可以被3整除，4+1＝5，那么□里可能是1、4、7，也就是3个连续自然数的和可能是411、441、471，据此解答．‎ ‎【解答】解：4□1是连续三个自然数的和，意味着平均值是中间的哪个数，也意味着4□1可以被3整除，‎ ‎4+1＝5，那么□里可能是1、4、7，‎ 所以只有选项B符合要求．‎ 故选：B．‎ 第20页（共20页）‎ ‎【点评】此题主查考查3的倍数特征．认真分析题意，知道“4□1是连续三个自然数的和，意味着平均值是中间的哪个数，也意味着4□1可以被3整除”是解题的关键．‎ ‎19．（1分）用两根长度相等的铁丝分别围成一个正方体和一个长方体框架，它们的表面积相比，（　　）‎ A．长方体的大 B．正方体的大 ‎ C．无法判断谁大 ‎【分析】用两根长度相等的铁丝围成一个正方体和一个长方体，也就是长方体和正方体的棱长总和相等，解答此题应根据题意，通过举例进行分析、进而得出结论．‎ ‎【解答】解：例如：长方体的长宽高分别为4厘米、3厘米、2厘米 棱长之和为（4+3+2）×4＝36（厘米）‎ 表面积则为：（4×3+4×2+3×2）×2＝52（平方厘米）‎ 与其棱长之和相等的正方体的棱长：36÷12＝3（厘米）‎ 其表面积：3×3×6＝54（平方厘米）‎ 所以如果一个长方体和一个正方体棱长和相等，那么它们的表面积正方体比长方体大．‎ 故选：B．‎ ‎【点评】此题主要考查长方体、正方体的表面积公式的灵活运用，明确：当长方体和正方体棱长总和相等时，正方体的表面积大于长方体的表面积．‎ ‎20．（1分）两个数的最大公因数是4，最小公倍数是24，这两个数不可能是（　　）‎ A．4和24 B．8和12 C．8和24‎ ‎【分析】根据题意，根据求两个数的最大公约数和最小公倍数的方法，进行依次分析，进而得出结论．‎ ‎【解答】解：A：根据两个数成倍数关系，这两个数的最大公约数是较小的那个数，最小公倍数是较大的那个数，4和24可以；‎ B：8＝2×2×2，12＝2×2×3，最大公约数是2×2＝4，最小公倍数是2×2×2×3＝24，即8和12可以；‎ C：根据两个数成倍数关系，这两个数的最大公约数是较小的那个数，最小公倍数是较大的那个数，得出最大公因数是8，最小公倍数是24，所以C不可能；‎ 故选：C．‎ ‎【点评】‎ 第20页（共20页）‎ 解答此题的关键是根据求两个数的最大公约数和最小公倍数的方法进行解答，也可以根据两个数成倍数关系，这两个数的最大公约数是较小的那个数，最小公倍数是较大的那个数，直接判断得出．‎ ‎21．（1分）下面的平面图中，（　　）号不能折成正方体．‎ A． B． ‎ C．‎ ‎【分析】根据正方体展开图的11种特征，选项A不属于正方体展开图，不能折成正方体；选项B和选项C都属于正方体展开图的“1﹣4﹣1”型，能折成正方体．‎ ‎【解答】解：根据正方体展开图的特征，选项A不能折成正方体；选项B和选项C都能折成正方体．‎ 故选：A．‎ ‎【点评】正方体展开图有11种特征，分四种类型，即：第一种：“1﹣4﹣1”结构，即第一行放1个，第二行放4个，第三行放1个；第二种：“2﹣2﹣2”结构，即每一行放2个正方形，此种结构只有一种展开图；第三种：“3﹣3”结构，即每一行放3个正方形，只有一种展开图；第四种：“1﹣3﹣2”结构，即第一行放1个正方形，第二行放3个正方形，第三行放2个正方形．‎ ‎22．（1分）在下面的几何体中，从正面看到的图形相同的有（　　）个．‎ A．2 B．3 C．4‎ ‎【分析】由左到右 图1从正面能看到4个正方形，分两层，上层1个，下层3个，左齐；‎ 图2从正面能看到6个正方形，分两层，上层2个，下层4个，左齐；‎ 图3从正面能看到一行3个正方形；‎ 图4从正面能看到4个正方形，分两层，下层3个，上层居中1个；‎ 图5从正面能看到5个正方形，分两层，上层2个，下层3个，两端齐；‎ 图6从正面能看到4个正方形，分两层，下层3个，上层居中1个．‎ 由以上分析可知，图4、图6从正面看到的形状相同．‎ 第20页（共20页）‎ ‎【解答】解：从正面看到形状相同的有：‎ 即在这6个几何体中，从正面看到的图形相同的有2个．‎ 故选：A．‎ ‎【点评】本题是考查作简单图形的三视图，能正确辨认从正面、上面、左面（或右面）观察到的简单几何体的平面图形．‎ 四、按要求完成下面各题．（23分）‎ ‎23．（12分）写出每组数的最大公因数和最小公倍数．‎ ‎（1）12和60‎ 最大公因数是　12　．‎ 最小公倍数是　60　．‎ ‎（2）13和14‎ 最大公因数是　1　．‎ 最小公倍数是　182　．‎ ‎（3）26和65‎ 最大公因数是　13　．‎ 最小公倍数是　130　．‎ ‎【分析】求最大公约数也就是这几个数的公有质因数的连乘积，最小公倍数是共有质因数与独有质因数的连乘积，由此解决问题即可．‎ ‎【解答】解：（1）12＝2×2×3，‎ ‎60＝2×2×3×5，‎ 最大公约数是2×2×3＝12，最小公倍数是2×2×3×5＝60．‎ ‎（2）14和13互质，所以，最大公因数是1，最小公倍数是14×13＝182；‎ ‎（3）26＝2×13，‎ ‎65＝5×13，‎ 所以26和65的最大公因数是13，最小公倍数是2×5×13＝130；‎ 故答案为：12；60；1；182；13；130．‎ 第20页（共20页）‎ ‎【点评】两个数互质，最大公因数是1，最小公倍数是他们的积；一个数是另一个的倍数，最大公因数是较小的数，最小公倍数是较大的数．‎ ‎24．（3分）把下列各数按从小到大的顺序排列．‎ ‎、1.2、、0.45、1、．　　‎ ‎【分析】这种题最好不用通分的方法去比较，太麻烦，因为＞2，所以最大，将其他数都化成小数更容易比较．‎ ‎【解答】解：≈0.429；＝0.625；＝1.5；‎ 因为0.429＜0.45＜0.625＜1.2＜1.5‎ 所以．‎ 故答案为：．‎ ‎【点评】此题涉及到分数和小数混合比较大小，要结合题目中数看看是都化成分数比较简单，还是都化成小数比较简单，灵活选择合适的方法即可．‎ ‎25．（8分）计算如图图形的表面积和体积．（单位：cm）‎ ‎【分析】（1）根据长方体的表面积公式：S＝（ab+ah+bh）×2，体积公式：V＝abh，把数据分别代入公式解答．‎ ‎（2）由于上面的正方体与下面的长方体粘合在一起，所以它的表面积是上面正方体4个面的面积加上下面长方体的表面积，它的体积等于正方体与长方体的体积和，根据长方体的表面积公式：S＝（ab+ah+bh）×2，体积公式：V＝abh，把数据分别代入公式解答．‎ ‎【解答】解：（1）（8×4+8×5+4×5）×2‎ ‎＝（32+40+20）×2‎ ‎＝92×2‎ ‎＝184（平方厘米）‎ 第20页（共20页）‎ ‎8×4×5＝160（立方厘米）‎ 答：这个长方体的表面积是184平方厘米，体积是160立方厘米．‎ ‎（2）4×4×4+（12×7+12×6+7×6）×2‎ ‎＝64+（84+72+42）×2‎ ‎＝64+198×2‎ ‎＝64+396‎ ‎＝460（平方厘米）‎ ‎4×4×4+12×7×6‎ ‎＝64+504‎ ‎＝568（立方厘米）‎ 答：它的表面积是460平方厘米，体积是568立方厘米．‎ ‎【点评】此题主要考查长方体、正方体的表面积公式、体积公式的灵活运用，关键是熟记公式．‎ 五、解决问题．（33分）‎ ‎26．（4分）48名女生和72名男生排成队列进行表演，要使女生队列和男生队列每列人数相等，那么每列最多有多少人？一共有几列？‎ ‎【分析】要使女生队列和男生队列每列人数相等，那么每列人数应是48和72的公因数，要求每列最多有多少人，就是求它们的最大公因数是多少，然后分别用男生人数和女生人数除以每列人数求出分别有几列，再相加即可．‎ ‎【解答】解：‎ 所以48和72的最大公因数是12×2＝24；‎ ‎48÷24+72÷24‎ ‎＝2+3‎ ‎＝5（列）‎ 答：每列最多有24人，一共有5列．‎ ‎【点评】解答此题的关键是先求出48和72的最大公因数，然后再进一步解答．‎ 第20页（共20页）‎ ‎27．（4分）甲、乙两人暑假去图书馆看书，甲每4天去一次，乙每5天去一次．如果6月27日他们在图书馆相遇，那么他们下一次在图书馆相遇是几月几日？‎ ‎【分析】甲每4天去一次，乙每5天去一次，那么他们下一次相遇与上一次相遇隔的天数应是4和5的最小公倍数，是20；如果6月27日他们在图书馆相遇，那么他们下一次在图书馆相遇是6月27日后的第20天，推算即可．‎ ‎【解答】解：4×5＝20（天）‎ ‎6月27日～6月30日经过了3天，‎ ‎20﹣3＝17（天）‎ 答：他们下一次在图书馆相遇是7月17日．‎ ‎【点评】解答此题的关键是明确他们下一次相遇与上一次相遇隔的天数应是4和5的最小公倍数，然后再进一步解答．‎ ‎28．（4分）同学们采集树种，第一组10人采集了8kg，第二组12人采集了10kg，第三组14人采集了12kg．哪一组平均每人采集得最多？‎ ‎【分析】小组采集的重量÷小组人数＝平均每人采集的重量，据此求出每组平均每人采集的重量，再比较即可．‎ ‎【解答】解：8÷10＝（千克）‎ ‎10÷12＝（千克）‎ ‎12÷14＝（千克）‎ ‎＝0.8‎ ‎≈0.83‎ ‎≈0.86‎ 所以＞＞‎ 答：第三组平均每人采集得最多．‎ ‎【点评】解答此题的关键是先求出每组平均每人采集的重量，然后再进一步解答．‎ ‎29．（8分）游乐中心的游泳池是一个长方体，长50m，宽25m，高2m．‎ ‎（1）如果在游泳池内注入1.6m深的水，那么注入的水有多少立方米？‎ ‎（2）如果在这个游泳池的四周及底面贴上瓷砖，要用多少平方米的瓷砖？‎ ‎【分析】（1）根据长方体的体积公式：V＝abh，把熟记代入公式解答．‎ 第20页（共20页）‎ ‎（2）首先搞清这道题是求长方体的表面积，其次这个长方体的表面由五个长方形组成，缺少下面，根据长方体的表面积公式：S＝（ab+ah+bh）×2，求出这5个面的总面积即可．‎ ‎【解答】解：（1）50×25×1.6‎ ‎＝1250×1.6‎ ‎＝2000（立方米）‎ 答：注入的水有2000立方米．‎ ‎（2）50×25+50×2×2+25×2×2‎ ‎＝1250+200+100‎ ‎＝1550（平方米）‎ 答：要用1550平方米瓷砖．‎ ‎【点评】解答有关长方体计算的实际问题，一定要搞清所求的是什么，再进一步选择合理的计算方法进行计算解答问题．‎ ‎30．（5分）在一个长10dm、宽6dm、高4dm的长方体玻璃水缸中，倒入3dm深的水，然后放入一个棱长4dm的正方体钢块，水缸里溢出多少升的水？‎ ‎【分析】根据正方体的体积公式：V＝a3，求出正方体钢块的体积，再根据长方体的体积公式：V＝abh，把数据代入公式求出长方体玻璃缸内无水部分的体积，然后用钢块的体积减去长方体玻璃缸内无水部分的体积就是溢出水的体积．‎ ‎【解答】解：4×4×4﹣10×6×（4﹣3）‎ ‎＝64﹣60×1‎ ‎＝64﹣60‎ ‎＝4（立方分米）‎ ‎4立方分米＝4升 答：水缸里溢出4升水．‎ ‎【点评】此题主要考查正方体、长方体体积公式的灵活运用，关键是式熟记公式．‎ ‎31．（8分）如图，一根方钢长6m，横截面是一个边长4cm的正方形．‎ ‎（1）这根方钢重多少千克？（1cm3钢重7.8g）‎ 第20页（共20页）‎ ‎（2）一辆载质量5t的货车能否一次运载50根这样的方钢？‎ ‎【分析】（1）根据长方体的体积公式：V＝abh，求出这根方钢的体积，然后用方钢的体积乘每立方厘米钢的质量即可．‎ ‎（2）根据乘法的意义，用乘法求出50根这样的方钢的质量，然后与5吨进行比较，如果50根方钢的质量等于或小于5吨，说明能一次运载，否则就不能一次运载．‎ ‎【解答】解：（1）6米＝600厘米 ‎4×4×600＝9600（立方厘米）‎ ‎9600×7.8＝74880（克）‎ ‎74880克＝74.88千克 答：这根方钢重74.88千克．‎ ‎（2）5吨＝5000千克 ‎74.88×50＝3744（千克）‎ ‎3744千克＜5000千克 答：一辆载质量5t的货车能一次运载50根这样的方钢．‎ ‎【点评】此题这样考查长方体体积公式的灵活运用，关键是熟记公式．‎ 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2020/5/29 8:15:34；用户：复圣中学；邮箱：fszx519@xyh.com；学号：37091097‎ 第20页（共20页）‎