五年级数学《梯形的面积练习》 7页

梯形的面积练习 教学内容： 小学五年级上册第五单元信息窗三梯形的面积练习课 教学目标 ：‎ 1、 能运用梯形的面积计算公式解决生活中简单的实际问题。‎ ‎2、通过梯形的面积练习，渗透迁移、转化的数学思想，掌握观察、总结的学习方法 。‎ ‎3、进一步发展学生的空间观念，提高学生解决实际问题的能力。‎ ‎4、感受数学与生活的密切联系，体会数学的价值和乐趣。‎ 教学重、难点：‎ ‎ 教学重点：能运用梯形的面积计算公式解决生活中简单的实际问题。‎ 教学难点：能正确计算有关梯形面积的实际问题。‎ 教具、学具：‎ 教师准备：多媒体课件、投影仪、题卡 学生准备：三角板、直尺、铅笔、两张完全一样的梯形卡片 教学过程：‎ 一、问题回顾，再现新知 ‎1、回顾旧知，做好铺垫 ‎ （1）谈话：同学们，上节课我们探究出了梯形的面积计算公式，谁来说一说计算公式是什么？它是怎样推导出来的？‎ 学生拿出课前准备好的两张梯形卡片拼一拼、说一说。‎ 最后找一名学生把公式板书出来：‎ 梯形的面积 =(上底+下底) × 高 ÷2‎ 字母表示式: S=(a+b)×h÷2‎ 推导过程回答预设：‎ ‎ 大部分同学的答案应该是：把梯形转化为平行四边形进行推导面积的，用两个完全一样的梯形拼成一个平行四边形，梯形的面积=平行四边形的面积÷2，平行四边形的高等于梯形的高，平行四边形的底等于梯形上底+下底的和，所以，梯形的面积 =(上底+下底) × 高 ÷2‎ 当然学生也可能有其他的转化方法，如把一个梯形可以剪拼成一个平行四边行，然后推导出面积计算公式。‎ 对于学生不同转化方法的回答，教师及时给予肯定。‎ 再次板书强调“转化”的数学思想。‎ （2） 谁能说说梯形的面积公式和三角形的面积公式有什么相同点和不同点？为什么公式中都有一个“÷2”？‎ 通过与三角形面积公式的对比，加深对面积公式的理解。‎ ‎ 回答预设：公式基本相同，三角形的面积计算公式是底×高÷2 ， 梯形的面积是(上底+下底) × 高 ÷2，区别在底上。‎ ‎(提醒学生不要忘了公式后面的÷2)‎ ‎ 师：刚才同学们的回答都很出色，这堂课就让我们带着这些知识继续走进有关梯形面积计算的数学乐园！‎ 二、分层练习，巩固提高 ‎（一）基本练习，巩固新知 ‎1、我来算一算：‎ 量出相关数据，并计算梯形的面积 ‎（1）‎ ‎ 上底( )厘米 下底（ ）厘米 高（ ）厘米 （2） ‎ ‎ ‎ 上底( )厘米 下底（ ）厘米 高（ ）厘米 ‎ 以上两题在考察学生计算能力的同时又培养了学生的动手测量能力，要求学生独立完成，然后投影展示画高及计算过程，其他学生做好评价。‎ 第（2）题关键让学生找清梯形的上底、下底，然后作出高，再测量，师巡视，了解测量及画高情况。学生讲清是如何找到梯形的上底、下底和高的。‎ 回答预设：梯形中平行的一组对边才是梯形的上底和下底，然后作上底、下底间的垂线段就是梯形的高。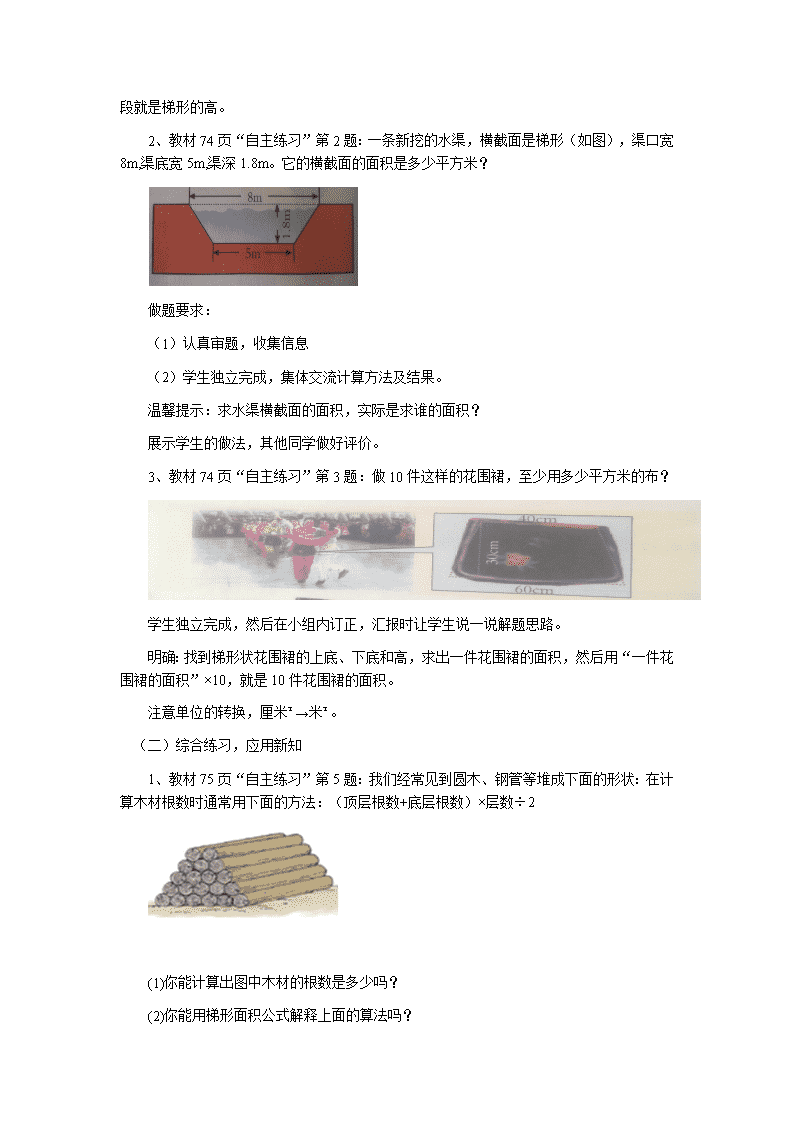‎ ‎2、教材74页“自主练习”第2题：一条新挖的水渠，横截面是梯形（如图），渠口宽8m,渠底宽5m,渠深1.8m。它的横截面的面积是多少平方米？‎ 做题要求：‎ （1） 认真审题，收集信息 （2） 学生独立完成，集体交流计算方法及结果。‎ 温馨提示：求水渠横截面的面积，实际是求谁的面积？‎ 展示学生的做法，其他同学做好评价。‎ ‎ 3、教材74页“自主练习”第3题：做10件这样的花围裙，至少用多少平方米的布？‎ 学生独立完成，然后在小组内订正，汇报时让学生说一说解题思路。‎ 明确：找到梯形状花围裙的上底、下底和高，求出一件花围裙的面积，然后用“一件花围裙的面积”×10，就是10件花围裙的面积。‎ 注意单位的转换，厘米²→米²。‎ ‎ （二）综合练习，应用新知 ‎1、教材75页“自主练习”第5题：我们经常见到圆木、钢管等堆成下面的形状：在计算木材根数时通常用下面的方法：（顶层根数+底层根数）×层数÷2‎ (1) 你能计算出图中木材的根数是多少吗？‎ (2) 你能用梯形面积公式解释上面的算法吗？‎ 出题意图：灵活应用梯形的面积公式解决生活中的实际问题。‎ 审题后，学生在小组内交流完成，师巡视，了解学生的想法、做法。‎ 汇报做法时，让学生用数学的语言解释一下算法，回答预设：堆积的横截面近似一个梯形，顶层根数看做梯形的上底，底层根数看做梯形的下底，层数是梯形的高，运用公式计算出梯形的面积就是总根数。‎ 汇报后，其他学生做好评价，师及时表扬学生的回答。‎ ‎40‎ ‎42‎ ‎35‎ ‎2、你能计算出下列梯形广告牌的面积吗？（单位：分米） ‎ ‎ ‎ ‎ 引导学生仔细观察图形，收集信息，思考后，指名回答解题思路。‎ 独立完成后，投影学生的做法，其他同学做好评价。‎ 总结解题关键：求梯形的下底是多少。‎ ‎ 3、分别计算下面每个梯形的面积，你发现了什么？（单位：cm）‎ ‎ （1）观察三个梯形，找出相同点和不同点。‎ ‎ （2）引导学生独立计算每个梯形的面积，交流发现。‎ ‎ （3）你可以得出一个什么样的结论？（板书：等底等高的梯形的面积相等）‎ ‎ （4）你还能再画出几个与途中面积相等的梯形吗？赶紧试试吧！‎ ‎ （学生感受面积相等的梯形，形状不一定相同）‎ 学生拿出题卡，动手操作。‎ ‎ （三）拓展练习，发展新知 ‎ 1、如图：靠墙边围成一个花坛，围花坛的竹篱笆全长46米，这个花坛的面积有多大？‎ ‎ ‎ ‎ 要求花坛的面积，已知什么信息，还需要哪些信息？‎ ‎ 温馨提示：靠墙的一边不用围篱笆。有两个直角，20m相当于梯形的高，那么46m减去20m，剩下的是什么？‎ ‎ 学生在小组内交流想法，师巡视倾听学生的想法，帮助理解有困难的学生，集体交流达成共识：没必要求出梯形的上底、下底分别是多少，只要求出上底、下底的和是多少就足够了即：46-20=26（米）26×20÷2=260（米²）‎ ‎2、一块梯形菜地的面积是140平方米，上底是10米，下底是25米，哪么它的高是多少米？ 10m ‎ 140m²‎ ‎ 25m ‎ 做题过程：（1）认真审题，收集信息 ‎ （2）小组内交流计算方法，集体反馈评价。‎ 师巡视，了解学生的做法。‎ 计算方法预设：方程法：设高为x米，列出方程（10+25）x÷2=140‎ ‎ ‚算式法：140÷（10+25）×2‎ 师：已知梯形的面积和上底、下底，同学们能求出梯形的高，如果已知梯形的面积和高，你们能求出梯形上底+下底的和是多少吗？‎ 学生回答后师板书出梯形的变形公式。‎ 这是一道梯形面积计算公式的变式题，为进一步巩固梯形面积公式并能灵活运用，做题时可引导学生用方程解答，算术法也应给予肯定。‎ ‎3、教材75页“自主练习”第6题：梯形菜园的面积是多少平方米？‎ ‎ ‎ ‎ （1）引导学生认真审题，收集信息，求梯形的面积已知哪些条件，还缺少哪些条件？‎ ‎ （2）小组内交流计算方法，师巡视，适时引导。‎ ‎ （3）汇报，集体评议。学生讲清解题方法，其他学生补充评价。‎ ‎ 提问：解题关键是什么？‎ ‎ 生回答：求出三角形菜花地的高，因为梯形菜地和菜花地是等高的。‎ ‎ 做法一：先求出三角形菜花地的高，60÷15×2=8（米）（此处提醒学生不要忘了×2），学生也可能用方程的方法求高，师要给予肯定。求出高就能利用梯形的面积公式求出菜园的面积了。‎ 做法二：学生求出菜花地的高后，再求白菜地的面积，最后把两个三角形的面积加在一起。‎ ‎ 三、梳理总结，提升认知 师：通过本堂课的练习,同学们能用梯形的面积计算公式灵活的解决生活中的实际问题，进一步感受了数学与生活的密切联系。现在，同学们对梯形你又有哪些新的认识？‎ 学生相互交流收获，回答预设：我知道了等底等高的梯形的面积都相等；‎ 面积相等的梯形，形状不一定相同；‎ 如果圆木、钢管堆成梯形状，计算它们的根数时也运用到梯形的面积公式 ‎······‎ 板书设计： 梯形的面积练习 梯形的面积 =(上底+下底) × 高 ÷2‎ 字母表示式: S=(a+b)×h÷2‎ ‎“转化”的数学思想 梯形的高：h＝2S÷(a＋b）‎ 梯形的上底：a＝2S÷h－b 梯形的下底：b＝2S÷h－a 结论：等底等高的梯形的面积都相等.‎ ‎ ‎