5年级数学教案《分数的基本性质练习》 8页

‎ 分数的基本性质练习 教学内容： 小学数学五年级下册第22—23页 教学目标：‎ ‎1．通过自主练习，引导学生进一步理解分数的基本性质，会运用分数的基本性质解决简单的实际问题。 ‎ ‎2．通过多层面、生活化的练习，引导学生在练习中想一想、议一议、说一说、深化对分数基本性质的认识。‎ ‎3.培养学生解决问题的能力。感受数学与生活的密切联系，体验学数学、用数学的乐趣。‎ 教学重难点： ‎ 重点：对分数基本性质的深化与理解，并能熟练地应用。‎ 难点： 能够灵活地应用性质参与问题的解决。 ‎ 教具准备：课件  实物投影 一、问题回顾，再现新知 ‎1．回顾旧知。‎ 同学们，上节我们已经初步了解了“分数的基本性质”，请大家回忆一下上节课学习的内容。并思考：‎ 问题引领：‎ ‎（1）分数的基本性质是什么？‎ ‎（2）根据分数的基本性质，你能举一个大小相同而分母不同的分数吗？你能说说它们的分子和分母是如何变化的吗？‎ ‎（3）分数的基本性质在生活中有什么用处呢？举个例子好吗？‎ ‎2．汇报交流。‎ 分数的基本性质：分数的分子和分母同时乘或除以相同的数（0除外），分数的大小不变。‎ 重点强调分数基本性质中“同时”“相同的数”“0除外”三个关键词的含义。必要时可以举例说明：说出一个和大小相同的分数，并简要说明理由。‎ ‎(2)应用：‎ 利用分数的基本性质可以找出两个分数之间的分数、化简分数、以后还可以进行通分、约分、学习百分数的知识……能解决好多的生活问题呢！‎ ‎3．揭示课题 今天这节课我们应用分数的基本性质解决问题，并板书：分数基本性质练习。‎ 二、分层练习，巩固提高 ‎ ‎（一）基本练习，巩固新知。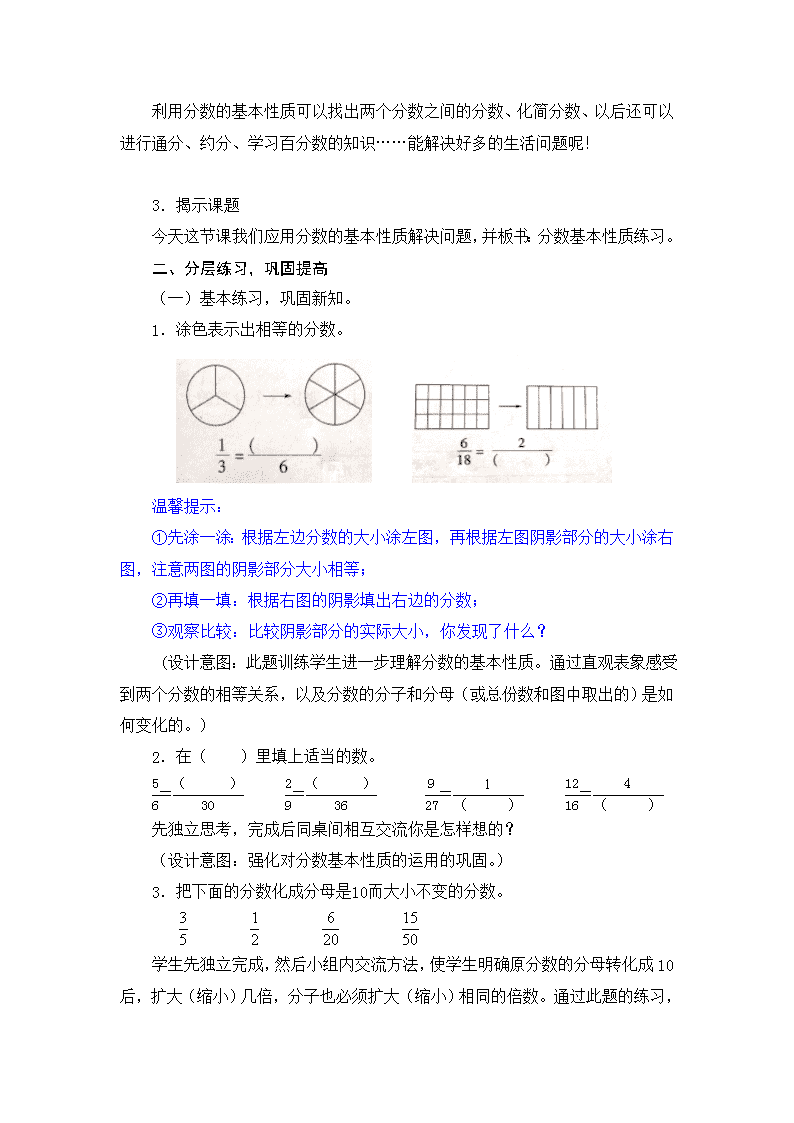‎ ‎1．涂色表示出相等的分数。‎ ‎ ‎ 温馨提示：‎ ①先涂一涂：根据左边分数的大小涂左图，再根据左图阴影部分的大小涂右图，注意两图的阴影部分大小相等；‎ ②再填一填：根据右图的阴影填出右边的分数；‎ ‎③观察比较：比较阴影部分的实际大小，你发现了什么？‎ ‎ (设计意图：此题训练学生进一步理解分数的基本性质。通过直观表象感受到两个分数的相等关系，以及分数的分子和分母（或总份数和图中取出的）是如何变化的。)‎ ‎2．在（ ）里填上适当的数。‎ ＝ ＝ ＝ ＝ 先独立思考，完成后同桌间相互交流你是怎样想的？‎ ‎（设计意图：强化对分数基本性质的运用的巩固。）‎ ‎3．把下面的分数化成分母是10而大小不变的分数。‎ ‎ ‎ 学生先独立完成，然后小组内交流方法，使学生明确原分数的分母转化成10后，扩大（缩小）几倍，分子也必须扩大（缩小）相同的倍数。通过此题的练习，加深对变化规律的理解。‎ ‎4．变式练习。‎ ‎（1）‎ 温馨提示：‎ 先通过那个分数来填空，先填哪些空？再填哪些空？填每个空的理由是什么？‎ ‎（1）先独立思考，完成后同桌间相互交流。通过交流让学生明确：‎ ①先观察分子（母）是如何变化的，再根据分数的基本性质分母（子）应该怎样变化；‎ ②分数基本性质中“相同的数“通常是指整数。应选择分子或分母有整倍数关系的两个分数来填空。‎ ‎（2）完成后，指名汇报，教师适时追问：你是怎样想的？‎ ‎（设计意图：此题训练学生进一步理解分数的基本性质，强化对分数基本性质的运用的巩固。）‎ 小结：同学们只要灵活掌握分数的基本性质，并认真推导，一定能正确解决这些问题。其实在我们实际生活中会遇到一些综合性的题目，老师相信大家也能正确解决。‎ ‎4.涂色部分可以用几分之几表示？并说明你是怎样想的？‎ ‎（设计意图：此题训练学生对分数的基本性质的理解与应用，培养学生的发散性思维。）‎ ‎（二）综合练习，应用新知 ‎1．‎ 温馨提示：‎ ①怎样比较哪个季节更吸引游客？‎ ②观察分数的特点，可以怎样比较？‎ ③分数大说明什么问题？‎ ‎（设计意图：让学生充分发表自己的想法，引导学生理解：这两个分数既可以按同分子分数比较也可以将转化成分母为20的分数再和比较大小。）‎ ‎2．在庆祝“六一”的诗歌朗诵比赛中，老师把布置比赛现场需用的红花分给三个小组长来制作完成。小玲、小亮、小芳分别是三个小组的小组长，这三人扎的红花数是一样多吗? 如果不一样，谁扎的数量最少? 并说明你的理由 ‎　　　‎ 温馨提示：‎ ①看一看：三位组长分别扎了总数量的几分之几？‎ ②想一想：观察分数的特点，如何比较分数的大小？‎ ③分数大说明什么问题？‎ 让学生认真审题，弄清题意。独立思考。汇报交流。‎ 引导总结：在分母和分子都不相同的情况下比较分数大小时，可以利用分数的基本性质转化成分子或分母相同的分数后再比较就可以了。‎ ‎（三）拓展练习，发展新知 ‎1．按规律填数。‎ ‎（1），，，（ ），（ ），（ ）‎ ‎（2），，，（ ），（ ），（ ）‎ 此题通过找规律训练学生应用分数的基本性质，加深对性质的理解。‎ 温馨提示：‎ ①仔细观察每一小题中分子分母的变化规律是什么？‎ ②想一想根据规律后面的分数应该填什么？‎ ③通过练习你有什么收获？‎ 小组交流方法，汇报想法，教师适时引导，多找学生汇报。‎ ‎2．的分子加上8，要想使分数的大小不变，分母应加上几？‎ 此题通过计算，加深对性质的理解。‎ 温馨提示：‎ ①的分子加上8后分子变成了什么？和原来的分子相比，扩大了多少倍？‎ ②要想使分数的大小不变，分母应该扩大多少倍？是多少？‎ ③想一想：分母应该加上几呢？‎ 小组交流方法，汇报想法，教师适时引导，多找学生汇报。‎ ‎3.‎ 这是一道具有一定难度、综合性比较强的题目。‎ a．先给学生一些时间，让学生独立审题，独立探究。‎ b．由于本题对多少学生来说有较大难度，必要时，教师适时难点分解。‎ c．练习时，应先引导学生理清思路：整个房子的平面图被等分成36个方格，客厅占总面积的，因为=，所以客厅要占12个方格；主卧室占总面积的，因为=，所以主卧室要占9个方格；小卧室占总面积的，因为=，所以小卧室要占6个方格。然后酌情划分。‎ d．小结：看来，生活中有很多问题要用到分数的基本性质来解决，关键是根据不同需要选择化成各种不同的分数。‎ 三、梳理总结，提高认识 师生总结：通过本节课的学习，你有哪些收获？还要哪些疑问？‎ 引导学生归纳：‎ ‎1.应用分数基本性质时，注意“同时”“相同的数”“0除外”几个关键点。‎ 同时注意通常乘或除以的是整数。‎ ‎2.可以利用分数基本性质比较分母和分子都不相同的分数，方法是把它们分别化成分子或分母相同的数。‎ ‎3.利用分数基本性质解决生活问题时，要根据不同情况选择同时乘或除以相同的数，化成需要的分数来解决。‎ 这节课同学们能熟练掌握分数的基本性质，解决生活中的数学问题，能有条理地思考，比较清楚地表达自己思考过程。希望同学们下课之后，以小组为单位，利用这节课我们所学的数学知识验证一下分数的分子和分母同时减去一个相同的数，分数的大小是否变化。‎ 四、当堂检测 ‎1.说一说：下面各种情况下，怎样才能使分数的大小不变。‎ ‎（1）把的分子乘以5；‎ ‎（2）把的分子除以4；‎ ‎（3）一个分数的分母缩小到原来的；‎ ‎（4）一个分数的分子扩大2倍。‎ ‎2. 判断 ‎（1）分数的分子和分母乘以或除以一个数，分数的大小不变。‎ ‎（2）分数的分子和分母加上同一个数，分数的大小不变。‎ ‎（3）一个分数的分母不变，分子扩大3倍，分数的值就扩大3倍。‎ ‎（4）将变成后，分数扩大了4倍。‎ 板书设计：‎ 分数的基本性质练习课 分数的分子和分母同时乘或除以相同的数（0除外），分数的大小不变。‎ ‎ 过程（变、不变） 结果（不变）‎ 使用说明：‎ 1． 教学反思：回味课堂，我感觉这节课的成功之处在于以下几点：‎ ‎（1）问题回顾，再现新知。‎ 通过设计一系列的问题回忆分数基本性质，加深对性质的理解。在此基础上引导学生解决各种实际问题，充分调动学生研究的自主性，适时引导突出重点，为进一步学习打下坚实的基础，有效达成本节课的教学目标。‎ ‎ （2）由浅入深，有机渗透数学思想。‎ 练习时力求让学生主动探索，逐步获取。在综合练习环节，先比较分子分母不同，但分值相同的分数大小，然后到分子分母不同，但分值不同的分数大小比较，最后总结出比较分子分母不同分数大小的方法，培养了学生归纳、推理、转化的数学思想。‎ ‎ （3）习题分层，在练习中巩固深化。‎ 课堂练习形式多样，有层次，有梯度，目的性、针对性较强，达到了巩固知识、培养技能、激发兴趣、发展思维的目的。练习力求紧扣重点，做到新颖、多样、层次分明，有坡度，加深了学生对分数的基本性质的认识，激发了学习的兴趣，活跃了课堂气氛。这样不仅能照顾到学生思维发展的过程，而且有效拓宽了学生的思维空间，真正做到了学以致用。‎ ‎（4）在教学中注意抓住“变化”作为主线。‎ 分数基本性质是在分数大小不变的前提下研究分子、分母的变化规律。所以在教学过程中，抓住“变化”作为主线，设计思考题引导学生观察、对比、分析，应用分数的基本性质解决生活中一些数学问题。‎ ‎2．使用建议：‎ 这节课要注重学生思维表达，每一题都要求学生说思路，解释自己的思考过程，所以这节课设计的题量不宜过大，教学时完全应放手让学生大胆交流、讨论。让学生真正成为课堂的主人。‎ ‎3．需破解的问题：‎ ‎（1）孩子对房间的布局设计不熟悉或很陌生影响影响了解决问题的效果。‎ ‎（2）由于时间关系本课未涉及分子分母同时减去同一个数的情况，使得学生对性质的理解不太全面（可放到课下借助计算器验证）。‎ ‎ ‎