小学数学精讲教案4_3_6 燕尾定理 教师版 20页

燕尾定理 例题精讲 燕尾定理：‎ 在三角形中，，，相交于同一点，那么．‎ 上述定理给出了一个新的转化面积比与线段比的手段，因为和的形状很象燕子的尾巴，所以这个定理被称为燕尾定理．该定理在许多几何题目中都有着广泛的运用，它的特殊性在于，它可以存在于任何一个三角形之中，为三角形中的三角形面积对应底边之间提供互相联系的途径.‎ 通过一道例题证明一下燕尾定理：‎ 如右图，是上任意一点，请你说明：‎ 【解析】 三角形与三角形同高，分别以、为底，‎ 所以有；三角形与三角形同高，；三角形与三角形同高，，所以；综上可得. ‎ 【例 1】 如右图，三角形中，，，求．‎ ‎【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 根据燕尾定理得 ‎ ‎ ‎（都有的面积要统一，所以找最小公倍数）‎ 所以 ‎【点评】本题关键是把的面积统一，这种找最小公倍数的方法，在我们用比例解题中屡见不鲜，如果能掌握它的转化本质，我们就能达到解奥数题四两拨千斤的巨大力量！‎ ‎【答案】‎ ‎【巩固】如右图，三角形中，，，求.‎ ‎【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 根据燕尾定理得 ‎ ‎ ‎（都有的面积要统一，所以找最小公倍数）‎ 所以 ‎【答案】‎ ‎【巩固】如图，,,则 ‎ ‎【考点】燕尾定理 【难度】3星 【题型】填空 【解析】 根据燕尾定理有,,所以 ‎【答案】‎ ‎【巩固】如右图，三角形中，，，求.‎ ‎【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 根据燕尾定理得 ‎ ‎ ‎（都有的面积要统一，所以找最小公倍数）‎ 所以 ‎【点评】本题关键是把的面积统一，这种找最小公倍数的方法，在我们用比例解题中屡见不鲜，如果能掌握它的转化本质，我们就能达到解奥数题四两拨千斤的巨大力量！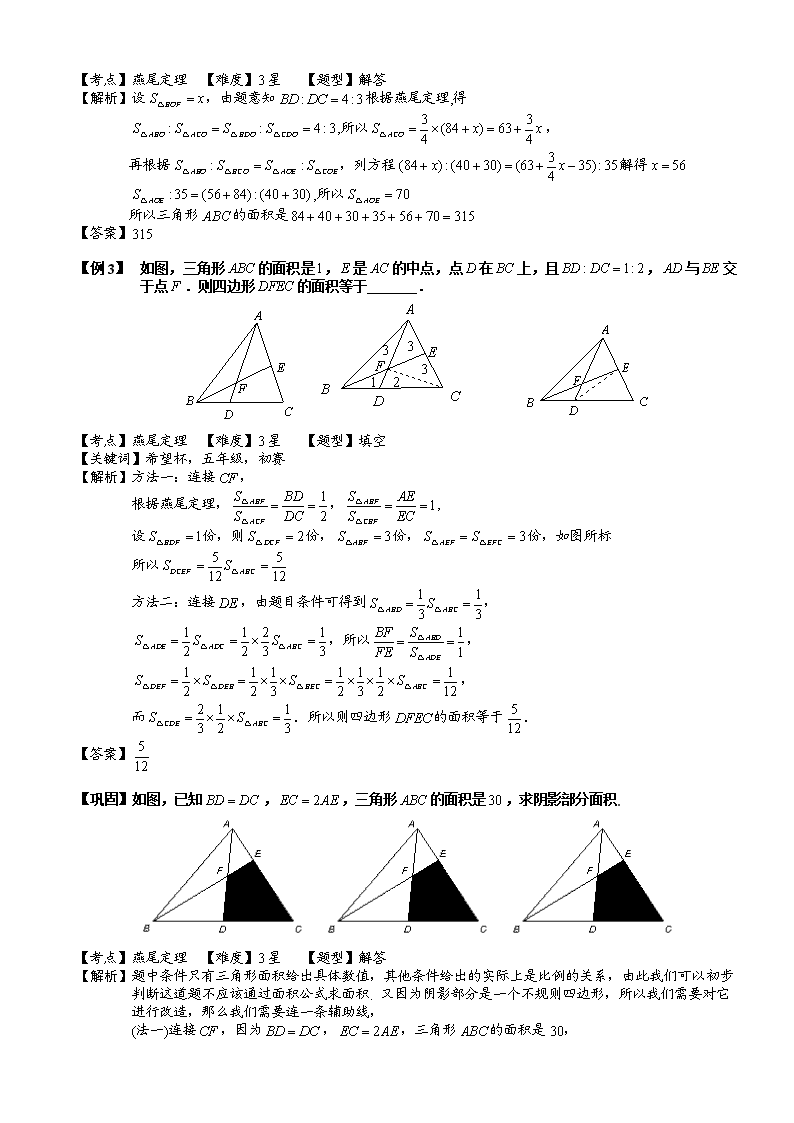‎ ‎【答案】‎ 【例 1】 如图，三角形被分成个三角形，已知其中个三角形的面积，问三角形的面积是多少?‎ ‎【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 设，由题意知根据燕尾定理,得 ‎,所以，‎ 再根据，列方程解得 ‎,所以 所以三角形ABC的面积是 ‎【答案】315‎ 【例 1】 如图，三角形的面积是，是的中点，点在上，且，与交于点．则四边形的面积等于 ．‎ ‎ ‎ ‎【考点】燕尾定理 【难度】3星 【题型】填空 ‎【关键词】希望杯，五年级，初赛 【解析】 方法一：连接，‎ 根据燕尾定理，，, ‎ 设份，则份，份，份，如图所标 所以 方法二：连接，由题目条件可得到，‎ ‎，所以，‎ ‎，‎ 而．所以则四边形的面积等于．‎ ‎【答案】‎ ‎【巩固】如图，已知，，三角形的面积是，求阴影部分面积.‎ ‎【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 题中条件只有三角形面积给出具体数值，其他条件给出的实际上是比例的关系，由此我们可以初步判断这道题不应该通过面积公式求面积. 又因为阴影部分是一个不规则四边形，所以我们需要对它进行改造，那么我们需要连一条辅助线，‎ ‎(法一)连接，因为，，三角形的面积是30，‎ 所以，．‎ 根据燕尾定理，，, ‎ 所以，，‎ 所以阴影部分面积是．‎ ‎ (法二)连接，由题目条件可得到，‎ ‎，所以，‎ ‎ ，‎ ‎ 而．所以阴影部分的面积为．‎ ‎【答案】12.5‎ ‎【巩固】如图，三角形的面积是， 在上，点在上，且,，与 交于点．则四边形的面积等于 ．‎ ‎【考点】燕尾定理 【难度】3星 【题型】填空 【解析】 连接，‎ 根据燕尾定理，，, ‎ 设份，则份,份，份，份，所以 ‎【答案】93‎ ‎【巩固】如图，已知，，与相交于点,则被分成的部分面积各占 面积的几分之几？‎ ‎【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 连接,设份，则其他部分的面积如图所示，所以份，所以四部分按从小到大各占面积的 ‎【答案】‎ ‎【巩固】如图所示，在中，，，与相交于点，若的面积为，则的面积等于 ．‎ ‎ ‎ ‎【考点】燕尾定理 【难度】3星 【题型】填空 ‎【关键词】香港圣公会数学竞赛 【解析】 方法一：连接．‎ 由于，，所以，．‎ 由蝴蝶定理知，，‎ 所以．‎ 方法二：连接设份，根据燕尾定理标出其他部分面积，‎ 所以 ‎【答案】2.4‎ 【巩固】 两条线段把三角形分为三个三角形和一个四边形，如图所示， 三个三角形的面积 分别是，，，则阴影四边形的面积是多少？‎ ‎【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 方法一：遇到没有标注字母的图形，我们第一步要做的就是给图形各点标注字母，方便后面的计算.‎ 再看这道题，出现两个面积相等且共底的三角形．‎ 设三角形为，和交于，则，再连结．‎ 所以三角形的面积为3.设三角形的面积为，‎ 则，所以，四边形的面积为．‎ 方法二：设，根据燕尾定理,得到，再根据向右下飞的燕子，有，解得四边形的面积为 ‎【答案】18‎ ‎【巩固】如图，三角形的面积是，，，与相交于点，请写出这部分的面积各是多少?‎ ‎【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 连接，设份，则其他几部分面积可以有燕尾定理标出如图所示，所以,,,‎ ‎【答案】‎ ‎【巩固】如图，在上，在上，且,，与交于点．四边形的面积等于，则三角形的面积 ．‎ ‎【考点】燕尾定理 【难度】3星 【题型】填空 【解析】 连接,根据燕尾定理，，, ‎ 设份，则份，份，份， 份,份,如图所标,所以份,份 所以 ‎【答案】45‎ ‎【巩固】三角形中，是直角，已知，，，，那么三角形(阴影部分)的面积为多少？‎ ‎【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 连接．‎ 的面积为 根据燕尾定理，；‎ 同理 设面积为1份，则的面积也是1份，所以的面积是份，而的面积就是份，也是4份，这样的面积为份，所以的面积为．‎ ‎【答案】0.3‎ 【例 1】 如图所示，在中，，是的中点，那么 ． ‎ ‎【考点】燕尾定理 【难度】3星 【题型】填空 【解析】 连接．‎ 由于，，所以，‎ 根据燕尾定理，．‎ ‎【答案】‎ ‎【巩固】在中，， ，求？‎ ‎ ‎ ‎【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 连接．‎ 因为，根据燕尾定理，，即；‎ 又，所以．则，‎ 所以．‎ ‎【答案】‎ ‎【巩固】在中，， ，求？‎ ‎【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 题目求的是边的比值，一般来说可以通过分别求出每条边的值再作比值，也可以通过三角形的面积比来做桥梁，但题目没告诉我们边的长度，所以应该通过面积比而得到边长的比．本题的图形一看就联想到燕尾定理，但两个燕尾似乎少了一个，因此应该补全，所以第一步要连接．‎ 连接．‎ 因为，根据燕尾定理，，即；‎ 又，所以．则，‎ 所以．‎ ‎【答案】‎ 【例 1】 如图9，三角形BAC的面积是1，E是AC的中点，点D在BC上，且BD:DC=1:2，AD与BE交于点F，则四边形DEFC的面积等于 。‎ ‎【考点】燕尾定理 【难度】3星 【题型】填空 ‎【关键词】希望杯，五年级，初赛，第二十题，6分 【解析】 题中条件只有三角形面积给出具体数值，其他条件给出的实际上式比例的关系，由此我们初步可以判断这道题不应该通过面积公式求面积。又因为阴影部分是一个不规则四边形，所以我们需要对它进行改造，那么我们需要连一条辅助线，‎ 方法一：连接，因为,，三角形的面积是1，‎ 所以。‎ 根据燕尾定理，,‎ ‎ 所以,‎ ‎ 所以阴影部分的面积分面积是。‎ ‎ 方法二：连接，由题目条件可得到，‎ ‎，‎ 而。所以阴影部分的面积为。‎ ‎【答案】‎ 【例 2】 如图1，中，点在上，点在上，与相交于点，如果，则 .‎ ‎【考点】燕尾定理 【难度】3星 【题型】填空 【解析】 连接,‎ ‎. 根据题意，不难得出,那么; 而;; 所以，;所以，平分四边形，那么. ,‎ ‎【答案】12‎ 【例 1】 如图4，三角形田地中有两条小路AE和CF，交叉处为D，张大伯常走这两条小路，他知道DF＝DC，且AD＝2DE。则两块田地ACF和CFB的面积比是___________。‎ ‎【考点】燕尾定理 【难度】3星 【题型】填空 ‎【关键词】希望杯，六年级，复赛，第十一题，5分 【解析】 方法一、ACF和CFB为同高三角形，所以面积比等于底边比AF:FB。 过F作BC的平行线，交AE于G，则因为DF=DC，所以三角形CED和FGD全等，GD=DE。又因为AD=2DE，所以D和G是AE的三等分点，所以AF:FB=AG:GE=1:2。 方法二、连接，设(份)，则。 设，，则有，解得， 所以。‎ ‎【答案】‎ 【例 2】 如图，长方形的面积是平方厘米，，是的中点．阴影部分的面积是多少平方厘米?‎ ‎【考点】燕尾定理 【难度】4星 【题型】解答 【解析】 设份，则根据燕尾定理其他面积如图所示平方厘米.‎ ‎【答案】‎ 【例 3】 如图所示，在四边形中，，，四边形的面积是，那么平行四边形的面积为________．‎ ‎       ‎ ‎【考点】燕尾定理 【难度】4星 【题型】填空 【解析】 连接,根据燕尾定理,,设,则其他图形面积，如图所标，所以.‎ ‎【答案】24‎ 【例 1】 是边长为厘米的正方形，、分别是、边的中点，与交于，则四边形的面积是_________平方厘米．‎ ‎ ‎ ‎【考点】燕尾定理 【难度】4星 【题型】填空 【解析】 连接、，设份，根据燕尾定理得份，份，则份，份，所以 ‎【答案】96‎ 【例 2】 如图，正方形的面积是平方厘米，是的中点，是的中点，四边形 的面积是_____平方厘米．‎ ‎ ‎ ‎【考点】燕尾定理 【难度】4星 【题型】填空 【解析】 连接,根据沙漏模型得,设份，根据燕尾定理份，份，因此份，，所以(平方厘米).‎ ‎【答案】14‎ 【例 3】 如图，四边形是矩形，、分别是、上的点，且，，与相交于，若矩形的面积为，则与的面积之和为 ．‎ ‎ ‎ ‎【考点】燕尾定理 【难度】3星 【题型】填空 ‎【关键词】清华附中，入学测试题 【解析】 ‎ (法1)如图，过做的平行线交于，则，‎ 所以，，即，‎ 所以．‎ 且，故，则．‎ 所以两三角形面积之和为．‎ ‎(法2)如上右图，连接、．‎ 根据燕尾定理，，，‎ 而，‎ 所以，，，，‎ 则，，‎ 所以两个三角形的面积之和为15．‎ ‎【答案】15‎ 【例 1】 正六边形，，，，，的面积是平方厘米，，，，，，分别是正六边形各边的中点；那么图中阴影六边形的面积是 ‎ 平方厘米．‎ ‎【考点】燕尾定理 【难度】3星 【题型】填空 ‎【关键词】迎春杯，六年级，初赛 【解析】 ‎（方法一）因为空白的面积等于面积的倍，所以关键求的面积，根据燕尾定理可得，但在用燕尾定理时，需要知道的长度比，连接,,过作的平行线，交于，根据沙漏模型得,再根据金字塔模型得,因此,在中，设份，则份,份，所以，‎ 因此（平方厘米）‎ ‎（方法二）既然给的图形是特殊的正六边形，且阴影也是正六边形我们可以用下图的割补思路，把正六边形分割成个大小形状相同的梯形，其中阴影有个梯形，所以阴影面积为（平方厘米）‎ ‎【答案】1148‎ 【例 1】 已知四边形，为正方形，，与是两个正方形的边长，求 ‎【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 观察图形，感觉阴影部分像蝴蝶定理，但是细细分析发现用蝴蝶定理无法继续往下走，注意到题目条件中给出了两个正方形的边长，有边长就可以利用比例，再发现在连接辅助线后可以利用燕尾，那么我们就用燕尾定理来求解 连接EO、AF，‎ 根据燕尾定理：， ‎ 所以 ，作OM⊥AE、ON⊥EF，‎ ‎∵AEEF ‎∴‎ ‎∴‎ ‎∴‎ ‎【答案】‎ 【例 2】 右图的大三角形被分成5个小三角形，其中4个的面积已经标在图中，那么，阴影三角形的面积是 ． ‎ ‎【考点】燕尾定理 【难度】3星 【题型】填空 【解析】 方法一：整个题目读完，我们没有发现任何与边长相关的条件，也没有任何与高或者垂直有关系的字眼，由此，我们可以推断，这道题不能依靠三角形面积公式求解.我们发现右图三角形中存在一个比例关系：‎ ‎，解得.‎ 方法二：回顾下燕尾定理，有，解得.‎ ‎【答案】2‎ 【例 1】 如右图，三角形中，，且三角形的面积是，则三角形的面积为______，三角形的面积为________，三角形的面积为______．‎ ‎ ‎ ‎【考点】燕尾定理 【难度】3星 【题型】填空 ‎【关键词】学而思杯，六年级 【分析】 连接、、．‎ 由于，所以，故；‎ 根据燕尾定理，，，所以 ‎，则，；‎ 那么；‎ 同样分析可得，则，，所以，同样分析可得，‎ 所以，．‎ ‎【答案】‎ ‎【巩固】 如右图，三角形中，，且三角形的面积是，求三角形的面积．‎ ‎【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 连接BG，份 根据燕尾定理，，‎ 得(份)，(份)，则(份)，因此,‎ 同理连接AI、CH得,,‎ 所以 三角形GHI的面积是1，所以三角形ABC的面积是19‎ ‎【答案】19‎ ‎【巩固】如图，中，，，那么的面积是阴影三角形面积的 倍．‎ ‎ ‎ ‎【考点】燕尾定理 【难度】3星 【题型】填空 ‎【关键词】走美杯，初赛，六年级 【分析】 如图，连接．‎ 根据燕尾定理，，，‎ 所以，，‎ 那么，．‎ 同理可知和的面积也都等于面积的，所以阴影三角形的面积等于面积的，所以的面积是阴影三角形面积的7倍．‎ ‎【答案】7‎ ‎【巩固】如图在中，,求的值．‎ ‎【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 连接BG,设1份，根据燕尾定理,,得(份)，(份),则(份)，因此,同理连接AI、CH得,,‎ 所以 ‎【点评】如果任意一个三角形各边被分成的比是相同的，那么在同样的位置上的图形，虽然形状千变万化，但面积是相等的，这在这讲里面很多题目都是用“同理得到”的，即再重复一次解题思路，因此我们有对称法作辅助线.‎ ‎【答案】‎ ‎【巩固】如图在中，,求的值．‎ ‎【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 连接BG,设1份，根据燕尾定理,,得(份)，(份),则(份)，因此,同理连接AI、CH得,,‎ 所以 ‎ ‎【答案】‎ ‎【巩固】如右图，三角形中，，且三角形的面积是，求角形 的面积．‎ ‎【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 连接BG，12份 根据燕尾定理，，‎ 得(份)，(份)，则(份)，因此,‎ 同理连接AI、CH得,,‎ 所以 三角形ABC的面积是,所以三角形GHI的面积是 ‎【答案】2‎ 【例 1】 三角形ABC的面积为15平方厘米，D为AB中点，E为AC中点，F为BC中点，求阴影部分的面积．‎ ‎【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 令BE与CD的交点为M，CD与EF的交点为N，连接AM，BN．‎ 在中，根据燕尾定理，,,‎ 所以 由于S，所以 在中，根据燕尾定理，‎ 设(份)，则(份)，(份)，(份)，‎ 所以,，因为,F为BC中点,‎ 所以,,‎ 所以(平方厘米)‎ ‎【答案】3.125‎ 【例 1】 如右图，中，是的中点，、、是边上的四等分点，与交于，与交于，已知的面积比四边形的面积大平方厘米，则的面积是多少平方厘米？‎ ‎【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 连接、．‎ 根据燕尾定理，，，所以；‎ 再根据燕尾定理，，所以，所以，那么，所以．‎ 根据题意，有，可得(平方厘米)‎ ‎【答案】‎ ‎【巩固】如图，中，点是边的中点，点、是边的三等分点，若的面积为1，那么四边形的面积是_________．‎ ‎ ‎ ‎【考点】燕尾定理 【难度】3星 【题型】填空 ‎【关键词】四中，分班考试 【解析】 由于点是边的中点，点、是边的三等分点，如果能求出、、三段的比，那么所分成的六小块的面积都可以求出来，其中当然也包括四边形的面积．‎ 连接、．‎ 根据燕尾定理，，而，所以，那么，即．‎ 那么，．‎ 另解：得出后，可得，‎ 则．‎ ‎【答案】‎ 【例 1】 如图，等腰直角三角形DEF的斜边在等腰直角三角形ABC的斜边上，连接AE、AD、AF，于是整个图形被分成五块小三角形．图中已标出其中三块的面积，那么△ABC的面积是________． （36）‎ ‎【考点】燕尾定理 【难度】3星 【题型】填空 ‎【关键词】迎春杯，五年级，初赛，第11题 【解析】 方法一：如图（1）延长AD交BC于G；如图（2）根据燕尾定理，得到；如图（3）；，由于ED∥BA，那么，同理，那么△ABC的面积为（1+2+3）´6=36。本题使用了燕尾定理、相似三角形等性质，学生不需要进行严格地证明，知道结论并会使用它解题即可。‎ ‎ ‎ ‎ 方法二：因为三角形DEF所给条件最多，先来关注这一三角形。由4个同样大小的三角形可以组成如下图的正方形，面积为4，所以边长为2，故EF=2。要使已知条件与三角形ABC产生联系，则将三角形AEF视为一个整体，面积为EF×h÷2=6，所以三角形ABC的高h=6。再观察下面的正方形，可以发现，对于等腰直角三角形，从顶点做的高为斜边长度的一半，故BC=2h=12，所以三角形ABC的面积=BC×h÷2=12×6÷2=36‎ ‎【答案】36‎ 【例 1】 如图，三角形的面积是，，，三角形被分成部分，请写出这部分的面积各是多少?‎ ‎ ‎ ‎【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 设BG与AD交于点P，BG与AE交于点Q，BF与AD交于点M，BF与AE交于点N．连接CP，CQ，CM，CN．‎ 根据燕尾定理，，，设(份)，则(份)，所以 同理可得，,,而，所以，．‎ 同理，,所以，,,‎ ‎【答案】‎ ‎【巩固】如图，的面积为1，点、是边的三等分点，点、是边的三等分点，那么四边形的面积是多少？‎ ‎ ‎ ‎【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 连接、、．‎ 根据燕尾定理，，，‎ 所以，那么，．‎ 类似分析可得．‎ 又，，可得．‎ 那么，．‎ 根据对称性，可知四边形的面积也为，那么四边形周围的图形的面积之和为，所以四边形的面积为．‎ ‎【答案】‎ 【例 1】 如右图，面积为的中，，，，求阴影部分面积．‎ ‎【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 设交于，交于，交于．连接，‎ ‎ ． ‎ ‎ ∵，，‎ ‎ ∵，，‎ ‎ ∴ ∵ ∴，‎ ‎ ∵ ∴ ．‎ 同理 ∴ ，‎ ‎ ∵ ，‎ ‎ ∴ ，‎ 又∵，‎ ‎ ∴，‎ ‎ 同理 ，∵，∴，‎ ‎ ∴．‎ ‎ 同理 个小阴影三角形的面积均为．‎ ‎ 阴影部分面积．‎ ‎【答案】‎ 【例 2】 如图，面积为l的三角形ABC中，D、E、F、G、H、I分别是AB、BC、CA 的三等分点,求阴影部分面积. ‎ ‎ ‎ ‎【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 三角形在开会，那么就好好利用三角形中最好用的比例和燕尾定理吧！‎ 令BI与CD的交点为M，AF与CD的交点为N，BI与AF的交点为P,BI与CE的交点为Q,连接AM、BN、CP ⑴求：在中，根据燕尾定理，‎ 设(份)，则(份),(份),(份),‎ 所以，所以,,‎ 所以,‎ 同理可得另外两个顶点的四边形面积也分别是面积的 ⑵求：在中，根据燕尾定理,‎ 所以,同理 在中，根据燕尾定理,‎ 所以 所以 同理另外两个五边形面积是面积的 所以 ‎【答案】‎ 【例 1】 如图，面积为l的三角形ABC中，D、E、F、G、H、I分别是AB、BC、CA 的三等分点,求中心六边形面积.‎ ‎【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 设深黑色六个三角形的顶点分别为N、R、P、S、M、Q，连接CR 在中根据燕尾定理，,‎ 所以,同理,‎ 所以 同理 根据容斥原理，和上题结果 ‎【答案】‎