- 1.90 MB
- 2022-02-11 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
数与形(
1
)
8
一、游戏激趣,导入课题
1+3=
1+3+5=
1+3+5+7=
1+3+5+7+9+
…
+21=
看谁算的快。
二、探索新知
状元成才路
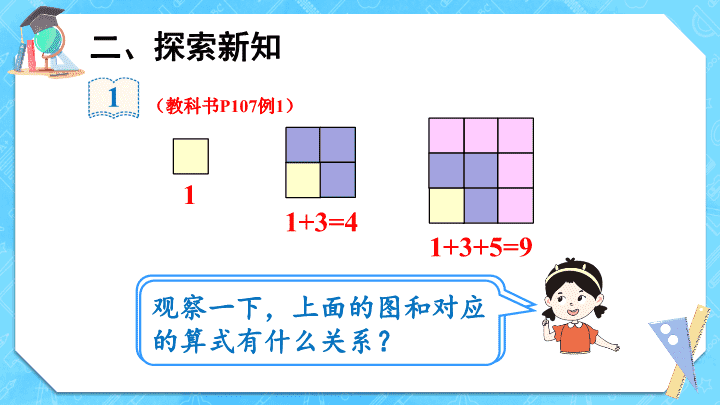
你能用一个算式表示这三幅图中小正方形的个数吗?
1
1+3=4
1+3+5=9
观察一下,上面的图和对应的算式有什么关系?
(教科书
P107
例
1
)
1
=( )
2
1+3
=( )
2
1+3+5
=( )
2
1
2
3
观察一这三个算式,你有什么发现?
利用规律直接写一写。
如果遇到困难
,
可以画图来帮助。
1
+
3
+
5
+
7=( )
2
1
+
3
+
5
+
7
+
9
+
11
+
13 =( )
2
1
+
3
+
5
+
7
+
9
+
11
+
13
+
15
+
17
4
7
______________________________=( 9 )
2
状元成才路
3
个奇数
三、巩固提高
1.
请根据例
1
的结论算一算。
1
+
3
+
5
+
7
+
5
+
3
+
1
=
( )
25
1
+
3
+
5
+
7
+
9
+
11
+
13
+
11
+
9
+
7
+
5
+
3
+
1=( )
85
状元成才路
4
个奇数
4
2
3
2
+
7
个奇数
6
个奇数
7
2
6
2
+
(教科书
P108
“做一做”第
1
题)
2.
下面每个图中各有多少个红色小正方形和多少个蓝色小正方形
?
(教科书
P108
“做一做”第
2
题)
照这样接着画下去,第
6
个图形有多少个红色小正方形和多少个蓝色小正方形
?
第
10
个图形呢
?
你能解释这其中的道理吗
?
红色
:
蓝色
:
1
8
2
10
3
12
4
14
2.
下面每个图中各有多少个红色小正方形和多少个蓝色小正方形
?
(教科书
P108
“做一做”第
2
题)
红色
:
蓝色
:
1
8
2
10
3
12
4
14
第
6
个图形
:6
个红色
18
个蓝色。
第
10
个图形
:10
个红色
26
个蓝色。
道理
:
任意两张相邻的图中,红色相差
1
个,
蓝色相差
2
个。
1.
下面每个图中最外圈有多少个小正方形?
照这样的规律接着画下去,第
5
个图形最外圈有多少个小正方形?你能解释这其中的道理吗?
状元成才路
3
2
-
1
2
5
2
-
3
2
7
2
-
5
2
=8
总个数:
3
行
3
列
内圈个数:
1
行
1
列
(教科书
P109“
练习二十二”第
1
题)
1.
下面每个图中最外圈有多少个小正方形?
照这样的规律接着画下去,第
5
个图形最外圈有多少个小正方形?你能解释这其中的道理吗?
状元成才路
3
2
-
1
2
5
2
-
3
2
7
2
-
5
2
=8
总个数:
5
行
5
列
内圈个数:
3
行
3
列
=16
1.
下面每个图中最外圈有多少个小正方形?
照这样的规律接着画下去,第
5
个图形最外圈有多少个小正方形?你能解释这其中的道理吗?
状元成才路
3
2
-
1
2
5
2
-
3
2
7
2
-
5
2
=8
总个数:
7
行
7
列
内圈个数:
5
行
5
列
=16
=24
3
2
-
1
2
=8
5
2
-
3
2
=16
7
2
-
5
2
=24
9
2
-
7
2
=32
11
2
-
9
2
=40
总个数:
11
行
11
列
内圈个数:
9
行
9
列
总个数:
9
行
9
列
内圈个数:
7
行
7
列
1.
下面每个图中最外圈有多少个小正方形?
照这样的规律接着画下去,第
5
个图形最外圈有多少个小正方形?你能解释这其中的道理吗?
2.
请你根据上面图形与数的规律接着画一画,填一填。
如果不画,这样排列下去,第
10
个数是多少
?
(教科书
P109“
练习二十二”第
2
题)
15
21
28
第
10
个数是
55
3.
下面每个三角形图各是由多少个小三角形组成的
?
如果小三角形的边长为
1
,每个三角形图的周长分别是多少
?
每个三角形图包含小三角形的个数与这个三角形图的周长之间有什么样的关系
?
(教科书
P109
“练习二十二”第
3
题)
你能提出什么数学问题
?
1
3
4
6
9
9
16
12
4.
如图所示,把同样大小的黑色棋子摆放在正多
边形的边上,按照这样的规律摆下去,则第八
个图形需要黑色棋子的个数是(
)。
80
状元成才路
1
2
+2×1
2
2
+2×2
3
2
+2×3
4
2
+2×4
……
8
2
+2×8
四、课堂小结
从
1
开始的连续奇数的和正好是这列数个数的平方。
状元成才路
五、课后作业
1.
从课后习题中选取;
2.
完成练习册本课时的习题。
状元成才路
三、观察图形,填写下表。
▶备选练习
《
创优作业
100
分
》P64
第三题
43
88
四、先数一数,再填一填,用你发现的规律解决问题。
《
创优作业
100
分
》P64
第四题
7
9
1.
摆
15
个三角形,需要多少根小棒?
2.
有
89
根小棒,能摆出多少个三角形?
3.
摆成的三角形个数与所用的小棒根数之间有什么关系?
31
根
44
个
摆成的三角形个数
×2 +1 =
所用的小棒根数
相关文档
- 六年级科学上册牛奶的变化课件3青2022-02-1130页
- 六年级下册英语课件-Unit3 Where d2022-02-1130页
- 六年级上册科学课件-《2铁钉生锈了2022-02-118页
- 部编版六年级上册语文课件24.少年2022-02-1144页
- 六年级数学下册课件-3 圆锥的体积-2022-02-1160页
- 2020人教精通版英语六年级上册单元2022-02-11116页
- 六年级上册数学课件-第1单元第7课2022-02-1112页
- 人教版六年级下册数学教学课件-第32022-02-1133页
- 六年级上册语文课件-第八单元 习作2022-02-1116页
- 六年级 上册音乐课件-第一单元《我2022-02-1113页