- 70.50 KB
- 2022-02-12 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
第34讲 行程问题(二)
一、知识要点
在行程问题中,与环行有关的行程问题的解决方法与一般的行程问题的方法类似,但有两点值得注意:一是两人同地背向运动,从第一次相遇到下次相遇共行一个全程;二是同地、同向运动时,甲追上乙时,甲比乙多行了一个全程。
二、精讲精练
【例题1】甲、乙、丙三人沿着湖边散步,同时从湖边一固定点出发。甲按顺时针方向行走,乙与丙按逆时针方向行走。甲第一次遇到乙后1分钟于到丙,再过3分钟第二次遇到乙。已知乙的速度是甲的,湖的周长为600米,求丙的速度。
甲第一次与乙相遇后到第二西与乙相遇,刚好共行了一圈。甲、乙的速度和为600÷(1+3)=120米/分。甲、乙的速度分别是:120÷(1+)=72(米/分),120—72=48(米/分)。甲、丙的速度和为600÷(1+3+1)=96(米/分),这样,就可以求出丙的速度。列算式为
甲、乙的速度和:600÷(1+3)=120(米/分)
甲速:120÷(1+)=72(米/分)
乙速:120—72=48(米/分)
甲、丙的速度和:600÷(1+3+1)=96(米/分)
丙的速度:96—72=24(千米/分)
答:丙每分钟行24米。
练习1:
1、甲、乙、丙三人环湖跑步。同时从湖边一固定点出发,乙、丙两人同向,甲与乙、丙两人反向。在甲第一次遇到乙后1分钟第一次遇到丙;再过3分钟第二次遇到途。已知甲速与乙速的比为3:2,湖的周长为2000米,求三人的速度。
2、兄、妹2人在周长为30米的圆形小池边玩。从同一地点同时背向绕水池而行。兄每秒走1.3米。妹每秒走1.2米。他们第10次相遇时,劢还要走多少米才能归到出发点?
7
3、如图34-1所示,A、B是圆的直径的两端,小张在A点,小王在B点,同时出发反向而行,他们在C点第一次相遇,C点离A点80米;在D点第二次相遇,D点离B点60米。求这个圆的周长。
【例题2】甲、乙两人在同一条椭圆形跑道上做特殊训练。他们同时从同一地点出发,沿相反方向跑。每人跑完第一圈到达出发点后,立即回头加速跑第二圈,跑第一圈时,乙的速度是甲的,甲跑第二圈时的速度比第一圈提高了,乙跑第二圈时速度提高了。已知甲、乙两人第二次相遇点距第一次相遇点190米。这条椭圆形跑道长多少米?
图34-2
图34-1
根据题意画图34-2:甲、乙从A点出发,沿相反方向跑,他们的速度比是1:=3:2。第一次相遇时,他们所行路程比是3:2,把全程平均分成5份,则他们第一次相遇点在B点。当甲A点时,乙又行了2÷3×2=1。这时甲反西肮而行,速度提高了。甲、乙速度比为[3×(1+):2]=2:1,当乙到达A点时,甲反向行了(3—1)×2=3。这时乙反向而行,甲、乙的速度比变成了[3×(1+)]:[2×(1+)]=5:3。这样,乙又行了(5—3)×=,与甲在C点相遇。B、C的路程为190米,对应的份数为3—=2。列式为1:=3:2 2÷3×2=1
[3×(1+):2]=2:1 (3—1)×2=3 [3×(1+)]:[2×(1+)]=5:3
(5—3)×= 190÷(3-)×5=400(米)
答:这条椭圆形跑道长400米。
练习2:
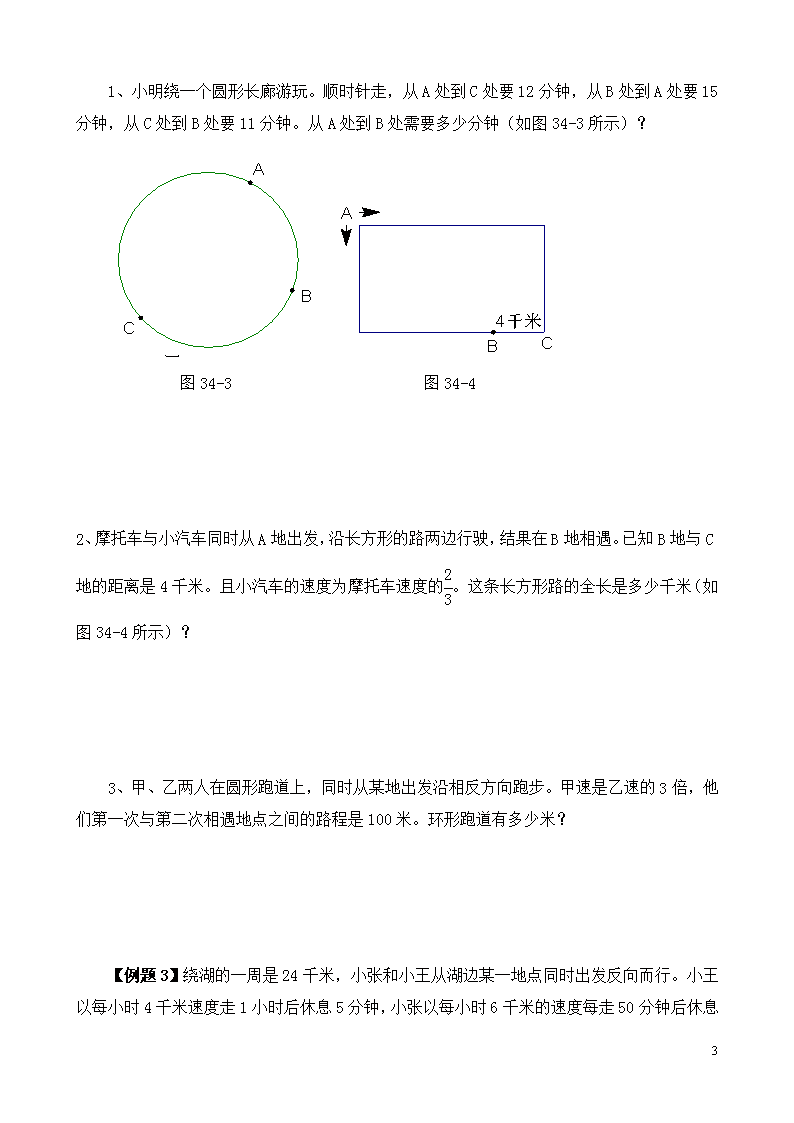
1、小明绕一个圆形长廊游玩。顺时针走,从A处到C处要12分钟,从B处到A处要15
7
分钟,从C处到B处要11分钟。从A处到B处需要多少分钟(如图34-3所示)?
图34-3 图34-4
2、摩托车与小汽车同时从A地出发,沿长方形的路两边行驶,结果在B地相遇。已知B地与C地的距离是4千米。且小汽车的速度为摩托车速度的。这条长方形路的全长是多少千米(如图34-4所示)?
3、甲、乙两人在圆形跑道上,同时从某地出发沿相反方向跑步。甲速是乙速的3倍,他们第一次与第二次相遇地点之间的路程是100米。环形跑道有多少米?
【例题3】绕湖的一周是24千米,小张和小王从湖边某一地点同时出发反向而行。小王以每小时4千米速度走1小时后休息5分钟,小张以每小时6千米的速度每走50分钟后休息10分钟。两人出发多少时间第一次相遇?
小张的速度是每小时6千米,50分钟走5千米
7
,我们可以把他们出发后的时间与行程列出下表:
小王
时间
1小时5分
2小时10分
3小时15分
行程
4千米
8千米
12千米
小张
时间
1小时
2小时
3小时
行程
5千米
10千米
15千米
12+15=27,比24大,从上表可以看出,他们相遇在出发后2小时10分至3小时15分之间。出发后2小时10分,小张已走了10+5÷(50÷10)=11(千米),此时两人相距24—(8+11)=5(千米)。由于从此时到相遇以不会再休息,因此共同走完这5千米所需的时间是5÷(4+6)=0.5(小时),而2小时10分+0.5小时=2小时40分。
小张50分钟走的路程:6÷60×50=5(千米)
小张2小时10分后共行的路程:10+5÷(50÷10)=11(千米)
两人行2小时10分后相距的路程:24—(8+11)=5(千米)
两人共同行5千米所需时间:5÷(4+6)=0.5(小时)
相遇时间:2小时10分+0.5小时=2小时40分
练习3:
1、在400米环行跑道上,A,B两点相距100米。甲、乙两人分别从A,B两点同时出发,按逆时针方向跑步,甲每秒行5米,乙每秒行4米,每人跑100米都要停留10秒钟。那么甲追上乙需要多少秒?
2、一辆汽车在甲、乙两站之间行驶。往、返一次共用去4小时。汽车去时每小时行45千米,返回时每小时行驶30千米,那么甲、乙两站相距多少千米?
3、龟、兔进行10000米跑步比赛。兔每分钟跑400米,龟每分钟跑80米,兔每跑5分钟歇25分钟,谁先到达终点?
7
【例题4】一个游泳池长90米。甲、乙二人分别从游泳池的两端同时出发,游到另一端立即返回。找这样往、返游,两人游10分钟。已知甲每秒游3米,乙每秒游2米。在出发后的两分钟内,二人相遇了几次?
设甲的速度为a,乙的速度为b,a:b的最简比为m:n,那么甲、乙在半个周期内共走m+n个全程。若m>n,且m、n都是奇数,在一个周期内甲、乙相遇了2m次;若m>n,且m为奇数(或偶数),n为偶数(或奇数),在半个周期末甲、乙同时在乙(或甲)的出发位置,一个周期内,甲、乙共相遇(2m—1)次。
甲速:乙速=3:2,由于3>2,且一奇数一偶数,一个周期内共相遇(2×3—1=)5次,共跑了[(3+2)×2=]10个全程。
10分钟两人合跑周期的个数为:60×10÷[90÷(2+3)×10]=3(个)
3个周期相遇(5×3=)15(次);个周期相遇2次。
一共相遇:15+2=17(次)
答:二人相遇了17次。
练习4:
1、甲、乙两个运动员同时从游泳池的两端相向下水做往、返游泳训练。从池的一端到另一端甲要3分钟,乙要3.2分钟。两人下水后连续游了48分钟,一共相遇了多少次?
2、一游泳池道长100米,甲、乙两个运动员从泳道的两端同时下水,做往、返训练15分钟,甲每分钟游81米,乙每分钟游89米。甲运动员一共从乙运动员身边经过了多少次?
7
3、马路上有一辆身长为15米的公共汽车,由东向西行驶,车速为每小时18千米。马路一旁人行道上有甲、乙两名年轻人正在练长跑,甲由东向西跑,乙由西向东跑。某一时刻,汽车追上了甲,6秒争后汽车离开了甲,半分钟后,汽车遇到迎面跑来的乙,又经过了2秒钟,汽车离开乙,再过几秒钟,甲、乙两人相遇?
【例题5】甲、乙两地相距60千米。张明8点从甲地出发去乙地,前一半时间平均速度为每分钟1千米,后一半时间平均速度为每分钟0.8千米。张明经过多少时间到达乙地?
因为前一半时间与后一半时间相同,所以可假设为两人同时相向而行的情形,这样我们可以求出两人合走60千米所需的时间为[60÷(1+0.8)=]33分钟。因此,张明从甲地到乙地的时间列算式为
60÷(1+0.8)×2=66(分钟)
答:张明经过66分钟到达乙地。
练习5:
1、A、B两地相距90千米。一辆汽车从A地出发去B地,前一半时间平均每小时行60千米,后一半时间平均每小时行40千米。这辆汽车经过多少时间可以到达B地?
2、甲、乙两人同时从A点背向出发,沿400米环行跑道行走。甲每分钟走80米,乙蔑分钟走50米。两人至少经过多少分钟才能在A点相遇?
7
3、在300米的环行跑道上,甲、乙两人同时并排起跑。甲平均每秒行5米,乙平均每秒行4.4米。两人起跑后第一次相遇在起跑线前面多少米?
7
相关文档
- 六年级奥数专题培优讲义——列方程2022-02-125页
- 六年级下册数学试题-奥数中的容斥2022-02-113页
- 2020小学奥数知识点要点汇总归纳梳2022-02-1119页
- 六年级下册数学试题-奥数:计算之裂2022-02-1111页
- 六年级下册数学试题-奥数:数论之同2022-02-119页
- 六年级下册奥数试题-《从算术到代2022-02-113页
- 六年级奥数教案:第16周 用组合法解2022-02-116页
- 六年级奥数教案:第32周 逻辑推理2022-02-114页
- 小学六年级奥数教案:第38讲 应用同2022-02-115页
- 六年级下册奥数课件-几何模块等积2022-02-1128页