北师大版数学六年级下册 《圆锥的体积》一课一练 (5) 7页

六年级下册数学一课一练- 1.4圆锥的体积 ‎ 一、单选题 ‎ ‎1.一个圆柱和一个圆锥的底面直径相等，圆锥的高是圆柱的3倍，圆锥的体积是12立方分米，圆柱的体积是（）立方分米。 ‎ A. 12                                          B. 36                                          C. 4                                          D. 8‎ ‎2.把一块圆柱体的木块削成一个尽可能大的圆锥．削去部分的体积是圆柱体积的(   )‎ A.                                             B.                                             C. 3倍 ‎3.甲、乙两个等高的圆锥，甲圆锥的底面半径是乙圆锥底面半径的3倍，则甲圆锥体积是乙圆锥体积的(    )倍。 ‎ A. 3                                          B. 6                                          C. 9                                          D. 1 2‎ ‎4.圆锥的底面周长6.28分米，高30厘米,它的体积是       立方分米（   ） ‎ A. 18.84                                   B. 3.14                                   C. 6.28                                   D. 25.12‎ ‎5.圆锥的体积比与它等底等高的圆柱体积少（  ）。 ‎ A.                                         B.                                         C. 2倍                                        D. 3倍 ‎6.一个圆锥的体积是12立方厘米，底面积是4平方厘米，高是（  ）厘米．‎ A. 3                                           B. 6                                           C. 9                                           D. 12‎ ‎7.一个棱长为6厘米的正方体，削成一个最大的圆锥体，削去部分的体积是（   ）‎ A. 159.48立方厘米                 B. 216立方厘米                 C. 56.52立方厘米                 D. 144立方厘米 二、判断题 ‎ ‎8.圆柱的体积大于圆锥的体积。‎ ‎9.一个圆锥的体积比与它等底等高的圆柱的体积小12立方厘米．这个圆锥的体积是4立方厘米．‎ ‎10.等高的圆柱和圆锥的底面半径之比是3∶1，则圆柱和圆锥体积之比为9∶1．‎ ‎11.圆锥的底面半径缩小2倍，高扩大2倍，体积不变．（判断对错） ‎ ‎12.一个圆柱与一个圆锥，它们的底面积和体积都相等．那么圆锥的高是圆柱高的 ．‎ 三、填空题 ‎ ‎13.一个圆锥形容器盛满水，水深为18厘米，将圆锥形容器的水倒入和它等底等高的圆柱形容器中，水深为________厘米。 ‎ ‎14.如图是一个直角三角形(单位：cm)，将它绕如图所示的直线L旋转一周，得到的立体图形的体积是________。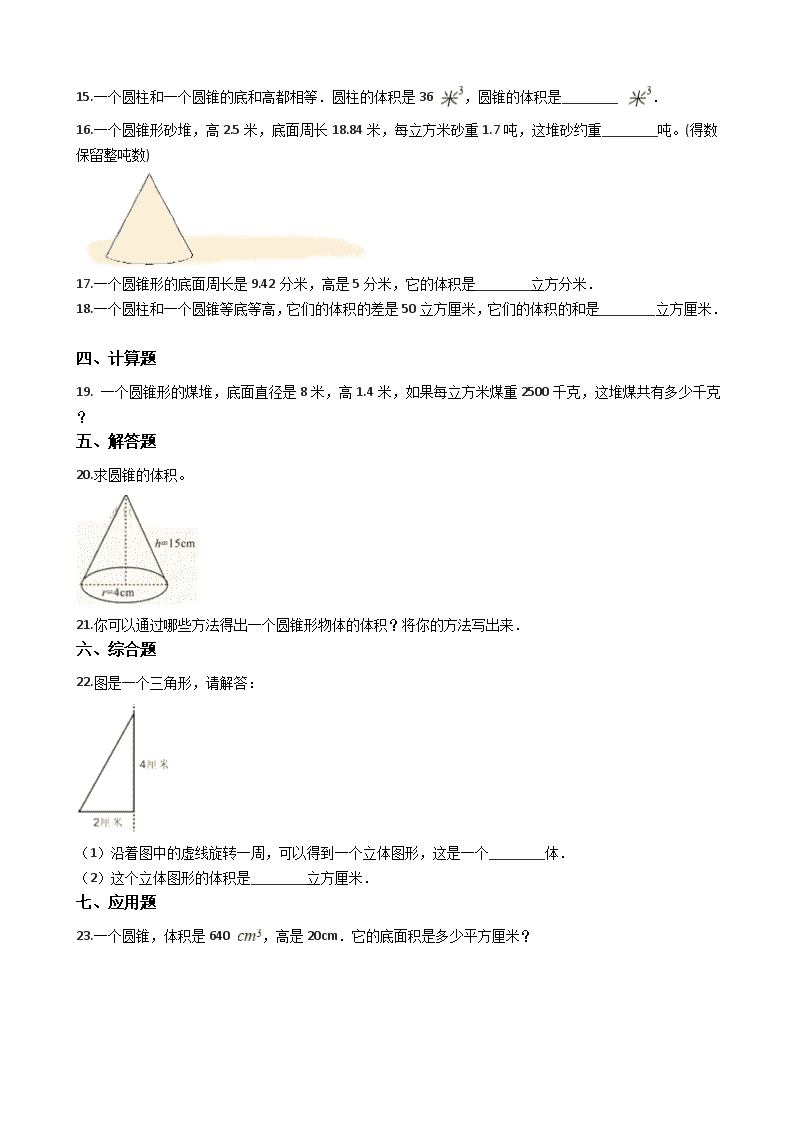‎ ‎ ‎ ‎15.一个圆柱和一个圆锥的底和高都相等．圆柱的体积是36 ，圆锥的体积是________  ． ‎ ‎16.一个圆锥形砂堆，高2.5米，底面周长18.84米，每立方米砂重1.7吨，这堆砂约重________吨。(得数保留整吨数) ‎ ‎17.一个圆锥形的底面周长是9.42分米，高是5分米，它的体积是________立方分米． ‎ ‎18.一个圆柱和一个圆锥等底等高，它们的体积的差是50立方厘米，它们的体积的和是________立方厘米． ‎ 四、计算题 ‎ ‎19. 一个圆锥形的煤堆，底面直径是8米，高1.4米，如果每立方米煤重2500千克，这堆煤共有多少千克？‎ 五、解答题 ‎ ‎20.求圆锥的体积。‎ ‎21.你可以通过哪些方法得出一个圆锥形物体的体积？将你的方法写出来． ‎ 六、综合题 ‎ ‎22.图是一个三角形，请解答： ‎ ‎（1）沿着图中的虚线旋转一周，可以得到一个立体图形，这是一个________体． ‎ ‎（2）这个立体图形的体积是________立方厘米． ‎ 七、应用题 ‎ ‎23.一个圆锥，体积是640 ，高是20cm．它的底面积是多少平方厘米？ ‎ ‎ ‎ 答案解析部分 一、单选题 ‎1.【答案】 A ‎ ‎【解析】解答：由题意，底面直径相等，所以半径也相等，设圆柱和圆锥的体积分别是 ， ，圆锥的体积是12立方分米，所以圆柱的体积也是12立方分米。 ‎ 分析：由圆柱的体积和圆锥的体积公式。‎ ‎2.【答案】 A ‎ ‎【解析】【解答】根据分析可知，把一块圆柱体的木块削成一个尽可能大的圆锥，削去部分的体积是圆柱体积的. 故答案为：A.‎ ‎【分析】把一块圆柱体的木块削成一个尽可能大的圆锥，则这个圆柱和圆锥等底等高，这个圆锥体积是圆柱体积的，削去部分的体积是圆柱体积的.‎ ‎3.【答案】C ‎ ‎【解析】【解答】解：甲圆锥的底面半径是乙圆锥底面半径的3倍，那么甲圆锥的底面积是乙圆锥底面积的9倍，所以甲圆锥的体积是乙圆锥体积的9倍. 故答案为：C ‎【分析】根据圆面积公式可知，圆面积扩大的倍数是半径扩大的倍数的平方倍；圆锥的高不变，体积扩大的倍数与圆锥的底面积扩大的倍数相同.‎ ‎4.【答案】 B ‎ ‎【解析】【解答】6.28÷3.14÷2=1(分米)，30厘米=3分米 3.14×1²×3×=3.14(立方分米) 故答案为：B ‎【分析】用底面周长除以3.14，再除以2求出底面半径，然后用圆锥的底面积乘高，再乘求出体积即可.‎ ‎5.【答案】 B ‎ ‎【解析】解答：（1- ）÷1＝ ‎ 答：一个圆锥的体积比与它等底等高的圆柱的体积少 ‎ 故选：B ‎ ‎ 分析：等底等高的圆锥的体积是圆柱体积的 ，把圆柱的体积看作单位“1"，根据求一个数比另一个少几分之几，用除法解答。‎ ‎6.【答案】 C ‎ ‎【解析】【解答】解：12×3÷4，‎ ‎=36÷4，‎ ‎=9（厘米）；‎ 答：这个圆锥的高是9厘米。‎ ‎【分析】根据题意，根据圆锥的体积公式= ×底面积×高，用圆锥的体积乘3再除以底面积即可得到这个圆锥的高，列式解答即可得到答案。‎ 故选：C ‎7.【答案】A ‎ ‎【解析】【解答】解：  =216-56.52=159.48（立方厘米）；所以削去部分的体积是159.48立方厘米；应选A。 故答案为：A。‎ ‎【分析】解答本题关键是明确所求圆锥的高与底面直径是正方体的棱长，根据正方体体积=棱长×棱长×棱长，圆锥体体积=πr2h，求出正方体和圆锥体体积，再根据减法意义，用减法计算削去部分的体积。‎ 二、判断题 ‎8.【答案】 错误 ‎ ‎【解析】【解答】等底等高的圆柱体积大于圆锥的体积，原题说法错误. 故答案为：错误.‎ ‎【分析】根据等底等高的圆柱和圆锥的体积关系，圆柱体积=圆锥的体积×3，据此解答.‎ ‎9.【答案】 错误 ‎ ‎【解析】【解答】12÷2=6立方厘米，原题计算错误. 故答案为：错误.‎ ‎【分析】等底等高的圆柱体积比圆锥体积多2倍，据此列式解答.‎ ‎10.【答案】错误 ‎ ‎【解析】【解答】解：设高为1， 圆柱底面半径：圆锥底面半径=3：1，则圆柱底面积：圆锥底面积=（3×3）：（1×1）=9：1， ‎ ‎ ‎ 圆柱的高：圆锥的高=1：1 则圆柱体积：圆锥体积=（9×1）：（1×1×）=9：=27：1。 故答案为：错误。‎ ‎【分析】等底等高的圆柱和圆锥底体积之比是3：1，已知圆柱和圆锥底面半径之比是3：1 底面积比是9：1，设高为1，根据圆锥的体积公式：v=sh，圆柱的体积公式：v=sh，由此解答。‎ ‎11.【答案】错误 ‎ ‎【解析】【解答】解：圆锥的底面半径缩小2倍，它的底面积就缩小2×2=4倍，高扩大2倍，那么圆锥的体积就缩小2倍， 因此，圆锥的底面半径缩小2倍，高扩大2倍，体积不变．这种说法是错误的． 故答案为：错误． 【分析】根据圆锥的体积公式：v= πr2h，再根据因数与积的变化规律，积扩大的倍数等于因数扩大倍数的乘积，据此判断．‎ ‎12.【答案】错误 ‎ ‎【解析】【解答】设圆柱和圆锥的体积都是V，底面积都是S，则 圆柱的高是：V÷S=， 圆锥的高是：3V÷S=， ÷=3，原题说法错误. 故答案为：错误.‎ ‎【分析】根据题意，设圆柱和圆锥的体积都是V，底面积都是S，分别表示出圆柱和圆锥的高，然后相除即可解答.‎ 三、填空题 ‎13.【答案】6 ‎ ‎【解析】【解答】当圆柱和圆锥的底面积和体积相等时，高之比为1:3，则在该题中，圆柱中水的高度为6厘米。 故答案为：6.‎ ‎【分析】根据等底等高的圆柱体积是圆锥体积的3倍可知，体积和底面积相等的圆柱和圆锥，圆柱的高是圆锥高的，据此解答.‎ ‎14.【答案】50.24 cm3 ‎ ‎【解析】【解答】解：3.14×4²×3× =3.14×16 =50.24(cm³) 故答案为：50.24cm³‎ ‎ ‎ ‎【分析】旋转一周会得到一个圆锥，底面半径是4cm，高是3cm；圆锥的体积=底面积×高×，根据估算计算即可.‎ ‎15.【答案】 12 ‎ ‎【解析】【解答】36×=12(立方米) 故答案为：12‎ ‎【分析】圆柱体积=底面积×高，圆锥体积=底面积×高×，等底等高的圆锥体积是圆柱体积的，由此计算即可.‎ ‎16.【答案】 40 ‎ ‎【解析】【解答】解：r=18.84÷2÷3.14=3(米) ‎ ‎ （吨）‎ 答：这堆砂约重40吨。‎ ‎【分析】 ‎ ‎17.【答案】11.775 ‎ ‎【解析】【解答】解：底面半径为：9.42÷3.14÷2=1.5（分米）， 体积为： ×3.14×1.52×5 =3.14×0.75×5 =11.775（立方分米）； 答：体积是11.775立方分米． 故答案为：11.775． 【分析】先根据底面周长求出底面半径，再利用圆锥的体积= πr2h，代入数据即可应用．‎ ‎18.【答案】 100 ‎ ‎【解析】【解答】50÷2×(1+3) =50÷2×4 =25×4 =100（立方厘米） 故答案为：100.‎ ‎【分析】根据题意可知，一个圆柱和一个圆锥等底等高，圆柱体积是圆锥体积的3倍，它们的体积的差是圆锥体积的2倍，体积之和是圆锥体积的（1+3）倍，据此列式解答.‎ 四、计算题 ‎19.【答案】解：煤堆的半径为：8÷2=4（米），‎ 煤堆的体积： ×3.14×42×1.4‎ ‎= ×3.14×16×1.4‎ ‎≈23.45（立方米），‎ ‎ ‎ 煤堆的重量：‎ ‎23.45×2500=58625（千克）．‎ 答：这堆煤共有58625千克 ‎【解析】【分析】要求这堆煤的重量，先求得煤堆的体积，煤堆的形状是圆锥形的，利用圆锥的体积计算公式求得体积，进一步再求煤堆的重量，问题得解．‎ 五、解答题 ‎20.【答案】解：42×3.14×15× =16×3.14×5 =251.2(cm3) ‎ ‎【解析】【分析】圆锥的体积=底面积×高×，由此根据公式计算即可.‎ ‎21.【答案】解：把一个圆锥形的铅锤，放进盛水的量杯里，看水面升高多少，可以得出这个圆锥形铅锤的体积. ‎ ‎【解析】【分析】可以利用排水法，把圆锥放入有水的量杯里，水面要没过圆锥且水不溢出，水面升高部分水的体积就是圆锥的体积.‎ 六、综合题 ‎22.【答案】（1）圆锥 （2）16.75 ‎ ‎【解析】【解答】解：（1）沿着图中的虚线旋转一周，可以得到一个立体图形，这个立体图形叫做圆锥． ‎ ‎·（2）圆锥的体积= ×3.14×22×4‎ ‎= ×3.14×4×4‎ ‎= ×50.24‎ ‎≈16.75（立方厘米）；‎ 答：这个立体图形的体积是16.75立方厘米．‎ 故答案为：圆锥、16.75．‎ ‎【分析】（1）沿着图中的虚线旋转一周，可以得到一个立体图形，这个立体图形叫做圆锥．（2）圆锥的体积= ×底面积×高，圆锥的底面半径和高已知，从而可以求出圆锥的体积．‎ 七、应用题 ‎23.【答案】解：   答：它的底面积是96平方厘米. ‎ ‎【解析】【分析】圆锥的体积=底面积×高×，底面积=圆锥的体积÷÷高，由此根据公式计算即可.‎ ‎ ‎