六年级数学教案《圆柱圆锥体积练习》 8页

圆柱、圆锥体积练习 教学内容： 小学数学六年级下册圆柱、圆锥体积练习。‎ 教学目标：‎ ‎1．进一步理解圆柱和圆锥体积的计算公式和它的推导过程，通过练习，熟练进行圆柱圆锥体积的计算。‎ ‎2.能根据具体情境，灵活的运用体积的计算方法，解决生活中一些简单的数学问题。‎ ‎3.在解决圆柱圆锥体积问题的过程中，学会用生活的眼光看数学问题，体会数学与生活的联系。‎ ‎4.进一步培养观察、分析和推理等思维能力，发展空间观念。‎ 教学重点：正确熟练掌握圆柱圆锥体积的计算方法。‎ 教学难点：灵活运用公式解决生活中一些简单的实际问题。‎ 教具准备：等底等高圆柱圆锥学具两套、水、沙子，多媒体课件。‎ 教学过程：‎ 一、问题回顾，再现新知 谈话引入：同学们，前两节课我们学习了圆柱和圆锥的体积，昨天发的圆柱圆锥体积的知识回顾单填好了吗？把你填的的结果和你小组的同学说一说。‎ ‎ ‎ 小组交流自己的回顾单，根据学生的填写的情况进行提问反馈。‎ ‎1.提问：怎样计算圆柱和圆锥的体积？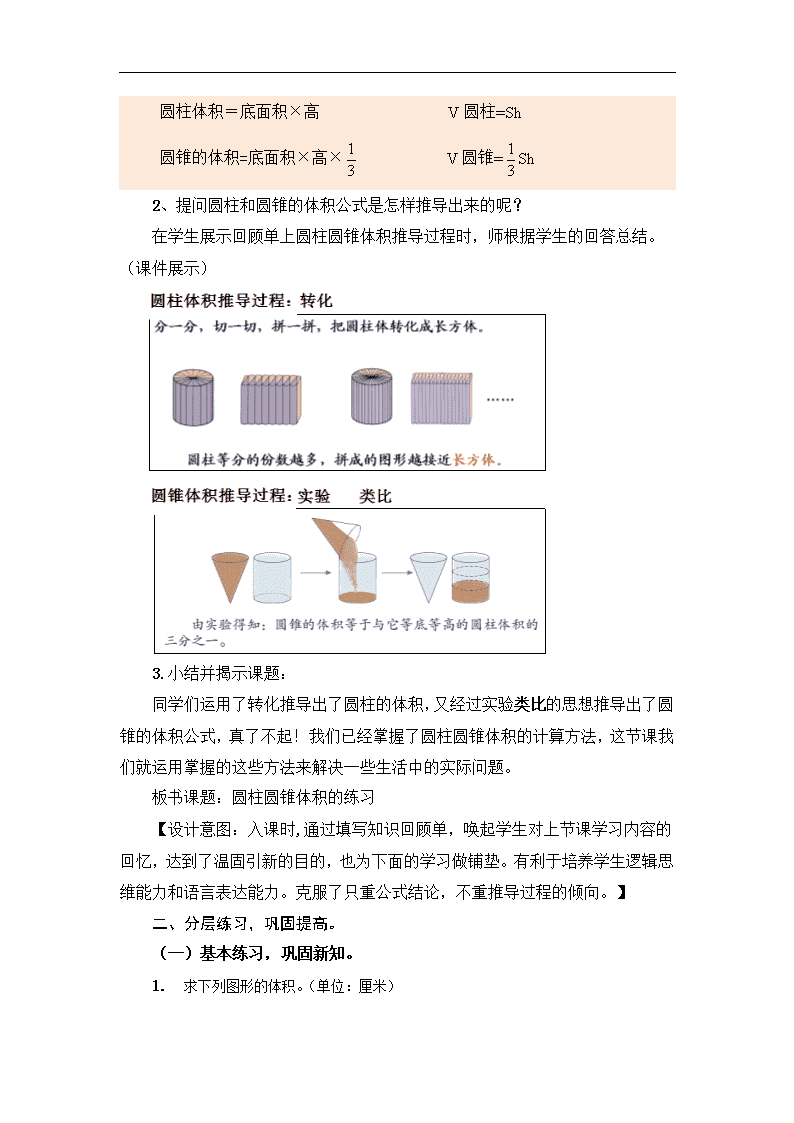‎ 根据学生的回答板书：‎ 圆柱体积＝底面积×高 V圆柱=Sh ‎ 圆锥的体积=底面积×高× V圆锥=Sh ‎ ‎2、提问圆柱和圆锥的体积公式是怎样推导出来的呢？‎ 在学生展示回顾单上圆柱圆锥体积推导过程时，师根据学生的回答总结。（课件展示）‎ ‎3.小结并揭示课题：‎ 同学们运用了转化推导出了圆柱的体积，又经过实验类比的思想推导出了圆锥的体积公式，真了不起！我们已经掌握了圆柱圆锥体积的计算方法，这节课我们就运用掌握的这些方法来解决一些生活中的实际问题。‎ 板书课题：圆柱圆锥体积的练习 ‎【设计意图：入课时,通过填写知识回顾单，唤起学生对上节课学习内容的回忆，达到了温固引新的目的，也为下面的学习做铺垫。有利于培养学生逻辑思维能力和语言表达能力。克服了只重公式结论，不重推导过程的倾向。】‎ 二、分层练习，巩固提高。‎ ‎（一）基本练习，巩固新知。‎ ‎1. 求下列图形的体积。（单位：厘米）‎ ‎（课件出示题目）‎ ‎ ‎ 同位互讲图中的数据表示什么？学生独立列式，指名汇报。‎ 小结：在做题时，一定要看清所求的是圆柱体还是圆锥体，然后再选择相应的公式来计算。‎ ‎2.判断题：‎ ‎①圆柱体积是圆锥体积的3倍。（ ） ②一个圆锥体，底面积不变，高扩大6倍，体积也扩大6倍。（  ） ③把一个圆柱削成一个最大的圆锥，削去部分的体积是原体积的2/3。（ ） ④一个圆锥的体积是75立方米，底面积是25平方米，则它的高是3米。（  ）‎ 学生先自主判断，通过手势了解判断情况,引导学生交流判断的理由。重点说说第①和④为什么错。‎ ‎3．如右图，直角三角形和长方形绕轴旋转一圈后，得到的立体图形是 ‎ 什么形状的？它们的体积分别是多少立方厘米？‎ ‎ ‎ ‎（1）引导理解题意：让学生想像三角形和长方形绕轴旋转后会得到怎样的图形。‎ ‎（2）学生独立完成。学生会根据圆锥的体积公式进行计算。‎ ‎（3）展示作业，交流：你是怎么想的？指名学生说出解题思路。‎ ‎ 【设计意图：通过基础练习，检查学生灵活运用圆柱、圆锥体积公式的情况。】‎ ‎ (二)综合练习，应用新知。‎ ‎1.课本32页第7题。‎ 这个粮仓的容积是多少立方米？（墙壁的厚度 忽略不计）‎ ‎（1）学生认真看图理解题意，重点引导学生明 确解题的思路，即粮仓的下半部分是圆柱形，上半部 分是圆锥形。让学生知道：求粮仓的容积就是求圆柱 和圆锥的体积之和。‎ ‎（2）明确解题思路后，让学生独立解决，指名汇 报，全班反馈质疑。鼓励生生互评。‎ ‎2. 课件出示： ‎ 右图是从圆柱中挖去一个圆锥后的剩余部分，请计算 剩余部分的体积。（单位：cm）‎ （1） 学生独立结合情境图理解题意，提出问题引导 思考 ：要求剩余部分的体积应先求出哪两部分的体积？‎ 让生明确：只要用圆柱体积减圆锥体积就可以了。‎ ‎（2）学生独立完成，找生汇报，其余同学提出质疑、‎ 补充、评价。‎ ‎ 3. 课本33页第1题。‎ ‎①杯子的容积是多少立方厘米？‎ ‎ ②每听饮料大约能倒几杯？‎ ‎（1）学生结合情境图理解题意，独立完成。‎ ‎（2）全班交流，让中等生向大家展示自己的 解题思路，使学生理解：圆柱体积是圆锥体积的 多少倍就能大约倒多少杯。‎ 教师总结：同学们真的很爱思考，能够将所 学知识融会贯通，学以致用。只要善于观察，认 真思考，下面的问题也一定会迎刃而解。‎ ‎4.课件出示：‎ 右图这个木桶的容底面直径是4分米，高5‎ 分米，这个木桶破损后最多能盛多少升水？‎ ‎（1）先让学生在小组内讨论，理解题意，‎ 抓住“漏洞”会造成什么结果？从而推出：‎ 这个水桶最多能装水多少千克指的是水桶哪 一部分的容积？‎ ‎（2）放手让学生分别用不同的策略计算，再展示引导学生比较。‎ ‎【设计意图：学是为了用，体积公式的记忆和运用并不是难点，重要的是让学生掌握探索的方法，让学生会灵活运用所学的知识解决生活中的实际问题。同时也让学生感到生活中有数学，生活中处处需要数学，提高学生应用数学的意识，激发学生的学习兴趣。】‎ ‎（三）拓展练习，发展新知。‎ ‎1.新课堂25页第4题：智慧园地。‎ 要把右图中的圆柱削成与它等高的圆锥零件，‎ 削去部分的体积是多少立方厘米？‎ 学生先看图理解题意，抓住关键词“等底等高”，让学生明确要削的这个圆锥的体积是这个圆柱的三分之一，所以削去的体积是这个圆柱的三分之二。‎ ‎2.如右下图所示，一个底面直径是20厘米的圆柱形玻璃杯中装有水，水中放有一个底面直径为6厘米、高20厘米的圆锥形铅锤。当取出铅锤后，杯里的水面会下降多少厘米？ ‎ ‎（1）学生看图、读题，理解题意，小组讨论一下解题思路。‎ ‎（2）学生独立尝试解决问题，小组内交流方法，使学生明确：圆锥的体积可以看作水面上升后新的圆柱的体积，根据圆柱的底面直径20厘米，可以利用s=π(d÷2)2‎ 求出圆柱的底面积，从而算出圆柱的高也就是水面下降了多少厘米。‎ ‎3.课件出示：‎ 瓶子里装着一些水，（如右图），瓶底面积是0.8平方分米。请你想办法计算瓶子的容积。‎ ‎①根据图审题获取信息。瓶高3dm，水深 ‎2dm，瓶底面积是0.8平方分米，酒深2.4dm.‎ ‎②先独立思考，再在小组交流解题思路与 方法。‎ ‎③讨论汇报：根据第一幅可以求出水的体积，即：0.8×2=1.6立方分米，将瓶子倒过来后，水的体积不会发生变化，瓶子上方形成了一个圆柱形状，它的底面积是0.8平方分米，高是3—2.4=0.6dm，因此上方的这个圆柱的体积是：0.8×0.6=0.48立方分米。然后用水的体积加上上方的这个圆柱体积就是瓶子的容积，即1.6＋0.48=2.08立方分米。‎ 总结：这里渗透了“等积变形”的解题策略。引导学生以后做题时要仔细观察，找准图形之间的转化关系。‎ ‎4.求沙漏中沙子的体积。‎ 师：沙漏又称沙钟，是我国古代的一种计量时间的仪器，它是根据流沙从一个容器漏到另一个容器的数量来计量时间的。‎ 你能求出这时沙漏上部和下部沙子的体积分别是多少吗？‎ 此题主要是向学生介绍“沙漏”，使学生体会我国古代的数学文明，感受数学在生活中的作用。‎ 组织交流时，使学生理解：求沙漏上部分沙子的体积就是求一个圆锥的体积；求下部分沙子的体积可以用大圆锥的体积减去小圆锥的体积。‎ ‎【设计意图：让学有余力的学生在综合训练的基础上，继续解答这些题，开阔解题思路、发展学生的空间观念、培养学生的创新思维。】‎ 三、梳理总结，提升认知。‎ ‎1.教师总结：通过这节课的练习，你对圆柱圆锥体积的计算又有那些新的认识？‎ 学生自由发言，引导学生结合练习内容进行总结，进一步感受数学与生活的密切联系。‎ 2． 提升认识：‎ 这节课同学们不仅能熟练地计算圆柱圆锥的体积，而且还能运用圆柱圆锥体积的计算方法解决生活中的数学问题。学会用数学的眼光观察周围的世界，老师为大家感到特别高兴，望同学们今后再接再厉!‎ 板书设计： ‎ 圆柱圆锥体积的练习 圆柱体积＝底面积×高 V柱=Sh 转化 ‎ 圆锥体积＝底面积×高× V锥=Sh ‎ 类比 使用说明：‎ ‎1．教学反思：‎ 上完这节课，以下几点是我的感想：‎ ‎（1）回顾旧知，理清脉络。课一开始，我首先让学生回顾圆柱圆锥体积的计算方法和推导过程，加深了学生对圆柱圆锥体积公式的理解。这样不仅使学生构建知识的过程更加完整和深刻，还能使其知识条理化、系统化，为学生应用公式进行计算和解决问题做好铺垫。‎ ‎（2）多样练习，提高效率。在练习题的设计上，有效地整合了教材和《新课堂》设计的练习题，注意练习的层次性。又找了一些圆柱圆锥体积的综合习题，训练学生灵活解题的能力。多取材于生活，将所学的知识运用到生活中去，让知识生活化，让学生感到生活中有数学，生活中处处需要数学，提高学生应用数学的意识。‎ ‎（3）注重方法，渗透思想。在解决数学问题时，要求学生独立思考，尝试解决，遇到困难善于同他人合作、讨论、交流解决，用数学语言清楚地表达解决问题的过程，培养了学生敢于质疑，善于倾听的数学素养。‎ ‎2.使用建议：‎ 由于这节课注重提高学生解决实际问题的能力，教学时可完全放手，充分相信学生，给学生充分的时间思考、交流，大胆表达自己的解题思路，鼓励学生勇于质疑，提出不同的解题方法，重视学生参与作用，体现学生主体地位。‎ ‎3.需要破解的问题：‎ 教学中，往往有部分学生对于圆柱圆锥的关系不能灵活应用，计算速度较慢，解决问题的方法理解还不到位，分析问题解决问题的能力较差。怎样针对这部分学生的知识基础和有限经验，加强解决问题能力的有效训练，以实现不同的人都能得到应有的发展？‎