《同步导学案》人教六年级数学（下册）第四单元 第五课时 比例尺 11页

‎3.比例的应用 第五课时 比例尺 1、 认识比例尺，理解比例尺的意义。‎ 2、 会求一副图的比例尺，能根据比例尺求图上距离或实际距离。‎ 3、 重难点：理解比例尺的意义，能根据比例尺求图上距离或实际距离。‎ ‎ ‎ 知识导入 ‎ ‎ 爸爸过几天要去北京出差，为在当地能方便出行，他买来一副北京市地图。明明好奇地凑过来，和爸爸一起查看。他突然发现在地图右下角有这样的标注：‎ 他用手指给爸爸：“这是什么意思呢？”爸爸说：“这叫线段比例尺，表示地图上1cm的距离相当于地面上50km的实际距离。有的地图标注的是数值比例尺。”那么，什么是数值比例尺呢？它和线段比例尺又有什么不同？‎ 这节课，我们就和明明一起来深入地认识比例尺。‎ 知识讲解 知识点一：比例尺的意义 什么叫做比例尺？‎ 分析：在绘制地图和其他平面图的时候，需要把实际距离按一定的比缩小（或扩大），再画在图纸上。这时，就要确定图上距离和相对应的实际距离的比。‎ 解析：一幅地图的图上距离和实际距离的比，叫做这幅图的比例尺。‎ 图上距离：实际距离=比例尺 或=比例尺 点拨：比例尺不是一把尺子，也不是一个数，而是两个数的比，不能带单位名称。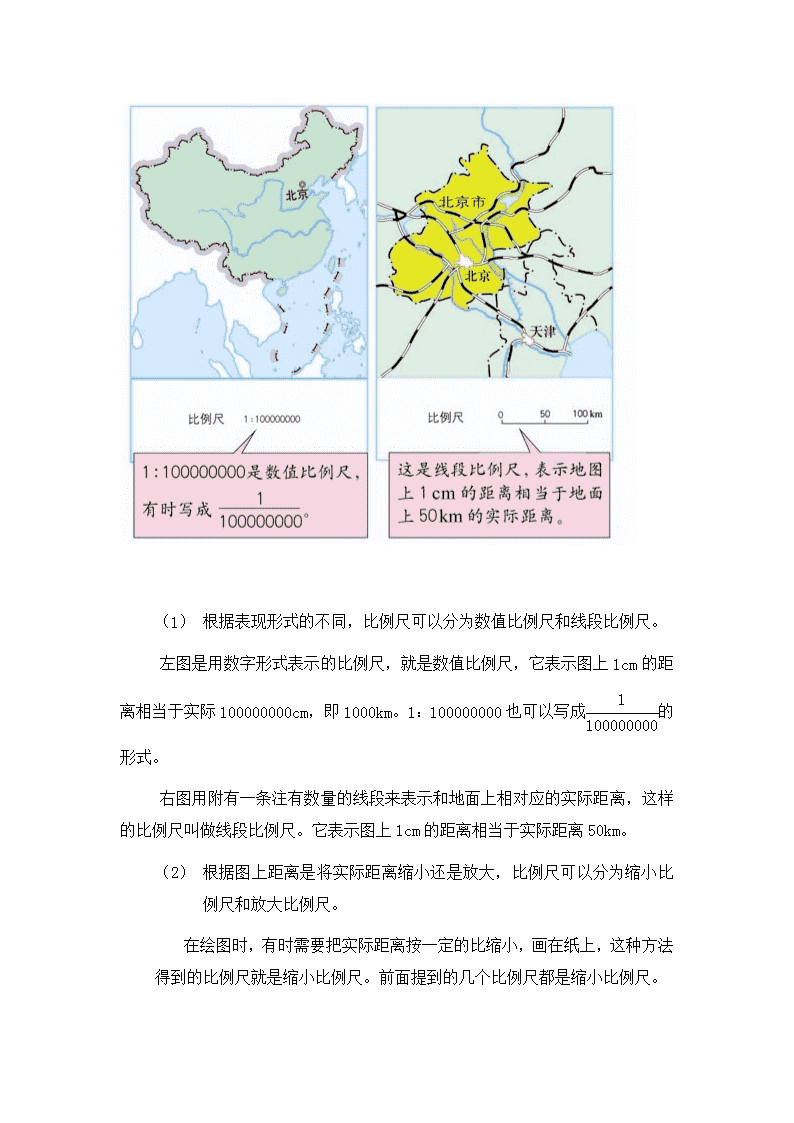‎ 知识点二：比例尺的分类 解析：‎ ‎ ‎ （1） 根据表现形式的不同，比例尺可以分为数值比例尺和线段比例尺。‎ 左图是用数字形式表示的比例尺，就是数值比例尺，它表示图上1cm的距离相当于实际100000000cm，即1000km。1：100000000也可以写成的形式。‎ 右图用附有一条注有数量的线段来表示和地面上相对应的实际距离，这样的比例尺叫做线段比例尺。它表示图上1cm的距离相当于实际距离50km。‎ （2） 根据图上距离是将实际距离缩小还是放大，比例尺可以分为缩小比例尺和放大比例尺。‎ 在绘图时，有时需要把实际距离按一定的比缩小，画在纸上，这种方法得到的比例尺就是缩小比例尺。前面提到的几个比例尺都是缩小比例尺。‎ 在生产中，有时由于机器零件比较小，需要把实际尺寸扩大一定的倍数后，再画到纸上，这样的比例尺就是放大比例尺。如图：‎ ‎ 图中的2:1就是一个放大比例尺，它表示图上2cm的长度相当于实际长度1cm。‎ 点拨：为了计算方便，一般把缩小比例尺写成前项是“1”，把扩大比例尺写成后项是1。‎ 知识点三：线段比例尺和数值比例尺的改写 例1 把教材48页右图的线段比例尺改写成数值比例尺。‎ 分析：根据线段比例尺，写出图上距离和实际距离的比，统一单位后再化成最简比的形式。‎ 解析：图上距离：实际距离 ‎ =1cm：50km ‎ =1cm：5000000cm ‎ =1：5000000‎ 点拨：线段比例尺改写成数值比例尺，一定注意把图上距离和实际距离的单位统一后再化简。此题还要注意，km和cm之间的进率是1000000。‎ 知识点四：根据比例尺和图上距离，求实际距离。‎ 分析：解答此题有两种方法：（1）可以设实际距离为χ，再根据“=比例尺”列方程求解。由于要求的实际距离的单位是千米，而已知图上距离的单位是厘米，可以先设是距离为χ厘米，算出实际距离是以厘米为单位的数，再化成以千米为单位的数。（2）要求实际长度是多少，先利用“图上距离÷比例尺”求出实际长度是多少厘米，再化成以千米为单位的数。‎ 解析：(1)解：设地铁1号线的实际长度大约是χ厘米。‎ = χ=10×500000‎ χ=5000000‎ ‎5000000cm=50km ‎(2)10÷=5000000(cm) 5000000cm=50km 答：地铁1号线的实际长度大约是50千米。‎ 点拨：已知比例尺和图上距离，求实际距离，可以根据“=比例尺”列比例解答，也可利用“实际距离=图上距离÷比例尺”直接列式计算。‎ 同样，已知比例尺和实际距离，求图上距离，可以根据“=比例尺”列比例解答，也可利用“图上距离=实际距离×比例尺”直接列式计算。‎ 知识点五：应用比例尺画图 例3 学校要建一个长80m、宽60m的长方形操场，画出操场的平面图。‎ 分析：想一想，这道题和前面解决的问题相比，有哪些难度？一是题中只告诉了实际距离，没有告诉比例尺，得自己先确定比例尺，再解决问题；二是还要算出操场的长和宽两个图上距离；三是不但要算出图上距离，还要画出操场的平面图。‎ ‎ 确定比例尺要根据自己纸的长和宽来决定，用自己的纸的长和宽来表示这个长方形操场的长和宽，然后根据纸上距离和实际距离就可以求出这幅图比较合适的比例尺。‎ 解析：(1)确定比例尺为1:1000或 0 10 20m ‎ ‎ ‎ (2)利用数值比例尺解答：‎ ‎80m=8000cm 60m=6000cm ‎ 长：8000×=8(cm) 宽：6000×=6(cm)；‎ ‎ 利用线段比例尺解答：‎ 长：80÷10==8(cm) 宽：60÷10==6(cm)‎ 因此画在图纸上，操场的长应画8cm，宽应画6cm。‎ ‎ （3）画一个长画8cm，宽6cm的长方形，并标明平面图名称及所用的比例尺。‎ 操场平面图 ‎（或1:1000）‎ ‎0 10 20m ‎ ‎ 点拨：应用比例尺画图时，要先根据实际距离与纸张的大小确定平面图的比例尺，再根据比例尺和实际距离求出图上距离，然后根据图上距离画出相应的平面图，并标明平面图名称及比例尺。‎ 知识探究 ‎1、比例尺的意义 ‎（1）一幅地图的图上距离和实际距离的比，叫做这幅图的比例尺。‎ ‎（2）图上距离：实际距离=比例尺 或=比例尺 例：从北京到天津的实际距离是120km，在一副地图上量得两地的图上距离是2cm，求这幅图的比例尺。‎ 解析：120km=12000000cm ‎ 2cm：12000000cm=1:6000000 答：这幅图的比例尺是1:6000000。‎ ‎2、比例尺的种类 ‎（1）根据表现形式的不同，比例尺可以分为数值比例尺和线段比例尺。‎ ‎（2）根据图上距离是将实际距离缩小还是放大，比例尺可以分为缩小比例尺和放大比例尺。‎ ‎（3）线段比例尺和数值比例尺可以相互转化。‎ ‎（4）为了计算方便，一般把缩小比例尺写成前项是“1”，把扩大比例尺写成后项是1。‎ 例：把下面的线段比例尺改写成数值比例尺。‎ ‎ ‎ ‎ 0 30 60km 解析：30 km=3000000cm 数值比例尺为1:3000000‎ ‎3、比例尺的应用 ‎（1）已知比例尺和图上距离，求实际距离，可以根据“=比例尺”列比例解答，也可利用“实际距离=图上距离÷比例尺”直接列式计算。‎ ‎（2）已知比例尺和实际距离，求图上距离，可以根据“=比例尺”列比例解答，也可利用“图上距离=实际距离×比例尺”直接列式计算。‎ 例：在一副比例尺是1:1000的校园平面图上，量得校门到楼门的距离是12cm，校门到楼门的实际距离是多少米？‎ 解析：12÷=12000（cm）=120(m)。答：校门到楼门的实际距离是120米。‎ 易错辨析 题1 判断：比例尺的前项都是1。（√）‎ 辨析：通常缩小比例尺的前项为1，放大比例尺的后项为1。‎ 正解：（×）‎ 题2 判断：从甲地到乙地的实际距离是150km，在一幅图上量得两地的图上距离是3cm，求这幅图的比例尺。‎ ‎3:150=1:50 答：这幅图的比例尺是1:50。‎ 辨析：此题错在没有把单位统一。‎ 正解：150km=15000000cm ‎ 3:15000000=1:5000000答：这幅图的比例尺是1:5000000‎ ‎1、填空题：‎ ‎(1)、（ ）和（ ）的比叫做比例尺。比例尺=（ ）：（ ），比例尺实际上是一个（ ）。‎ ‎(2)、在比例尺是1：4000000的地图上，图上距离1厘米表示实际距离（ ）千米。也就是图上距离是实际距离的（ ），实际距离是图上距离的（ ）倍。‎ ‎0 10 20 30km ‎ ‎(3)、一幅图的比例尺是 ，那么图上的1厘米表示实际距离（ ）；实际距离50千米在图上要画（ ）厘米。把这个线段比例尺改写成数值比例尺是（ ）。‎ ‎(4)、一种微型零件的长5毫米，画在图纸上长20厘米，这幅图的比例尺是（ ）。‎ ‎2、实际应用：‎ ‎(1)、在一幅地图上，测得甲、乙两地的图上距离是13厘米，已知甲乙两地的实际距离是780千米。①求这幅图的比例尺。‎ ‎②在这幅地图上量得A、B两城的图上距离是5厘米，求A、B两城的实际距离。‎ ‎（2）、在比例尺是1:3000000的地图上，量得两地距离是10厘米，甲乙两车同时从两地相向而行，3小时后两车相遇。已知甲乙两车的速度比是2:3，求甲乙两车的速度各是多少千米？‎ 在比例尺是1:30000000的地图上，甲、乙两地之间的航空线长4.5厘米，改画在比例尺是1:25000000的地图上，甲、乙两地之间的航空线应画多少厘米？‎ 分析：由比例尺是1:30000000，图上距离是4.5厘米，可求出甲、乙两地之间的实际距离，再根据这个实际距离和比例尺1:25000000，求出两地之间航空线的图上距离。‎ 解析：4.5÷=4.5×30000000=135000000（cm）‎ ‎135000000×=5.4（cm）答：两地之间航空线的图上距离为5.4厘米。‎ 点拨：此题的关键是求实际距离，在求实际距离时不必将厘米化成千米，以免下步计算时再换算单位。‎ 练习 ‎：在一副比例尺为1:20000的地图上，量得A、B两地的距离是5cm，如果在比例尺为1:5000的地图上，A、B两地间的图上距离应是多少厘米？‎ 参考答案 课时练习 ‎1、（1）图上距离 实际距离 图上距离 实际距离 比 ‎ （2）40 4000000 （3）10km 5 1：1000000 （3）40:1‎ ‎2、（1）①780千米=78000000厘米 13：78000000=1:6000000 ‎ 答：这幅图的比例尺为1:6000000。‎ ‎② 5÷=30000000（厘米）=300（千米）‎ 答：A、B两城的实际距离是300千米。‎ ‎ （2）10÷=30000000（厘米）=300（千米） 300÷3=100（千米）‎ ‎ 100×=40（千米）100×=60（千米） 答：甲车的速度是1小时40千米，乙车的速度是1小时60千米。‎ 拓展提升 ‎5÷=100000（cm）100000×=20（厘米）‎ 答：A、B两地间的图上距离是20厘米。‎