小学数学精讲教案5_1_3_3 数阵图（三） 教师版 8页

‎ ‎ ‎5-1-3-3.数阵图 教学目标 1. 了解数阵图的种类 2. 学会一些解决数阵图的解题方法 3. 能够解决和数论相关的数阵图问题 知识点拨 ‎.‎ 一、数阵图定义及分类：‎ 1. 定义：把一些数字按照一定的要求，排成各种各样的图形，这类问题叫数阵图.‎ 2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多，这里只向大家介绍三种数阵图：即封闭型数阵图、辐射型数阵图和复合型数阵图.‎ 3. 二、解题方法：‎ 解决数阵类问题可以采取从局部到整体再到局部的方法入手：‎ 第一步：区分数阵图中的普通点(或方格)和关键点(或方格)；‎ 第二步：在数阵图的少数关键点(一般是交叉点)上设置未知数，计算这些关键点与相关点的数量关系，得到关键点上所填数的范围；‎ 第三步：运用已经得到的信息进行尝试．这个步骤并不是对所有数阵题都适用，很多数阵题更需要对数学方法的综合运用．‎ 例题精讲 数阵图与数论 【例 1】 把0—9这十个数字填到右图的圆圈内，使得五条线上的数字和构成一个等差数列，而且这个等差数列的各项之和为55，那么这个等差数列的公差有　　　种可能的取值．‎ ‎【考点】数阵图与数论 【难度】3星 【题型】填空 ‎【关键词】迎春杯，三年级，初赛，第8题 【解析】 设顶点分别为A、B、C、D、E，有45+A+B+C+D+E=55，所以A+B+C+D+E=10，所以A、B、C、D、E分别只能是0-4中的一个数字.则除之外的另外5个数（即边上的）为45-10=35.设所形成的等差数列的首项为a1，公差为d.利用求和公式5（a1＋a1+4d）2=55，　得a1+2d=11，故大于等于0+1+5=6，且为奇数，只能取7、9或11，而对应的公差d分别为2、1和0.经试验都能填出来所以共有3中情况，公差分别为2、1、0.‎ ‎【答案】种可能 【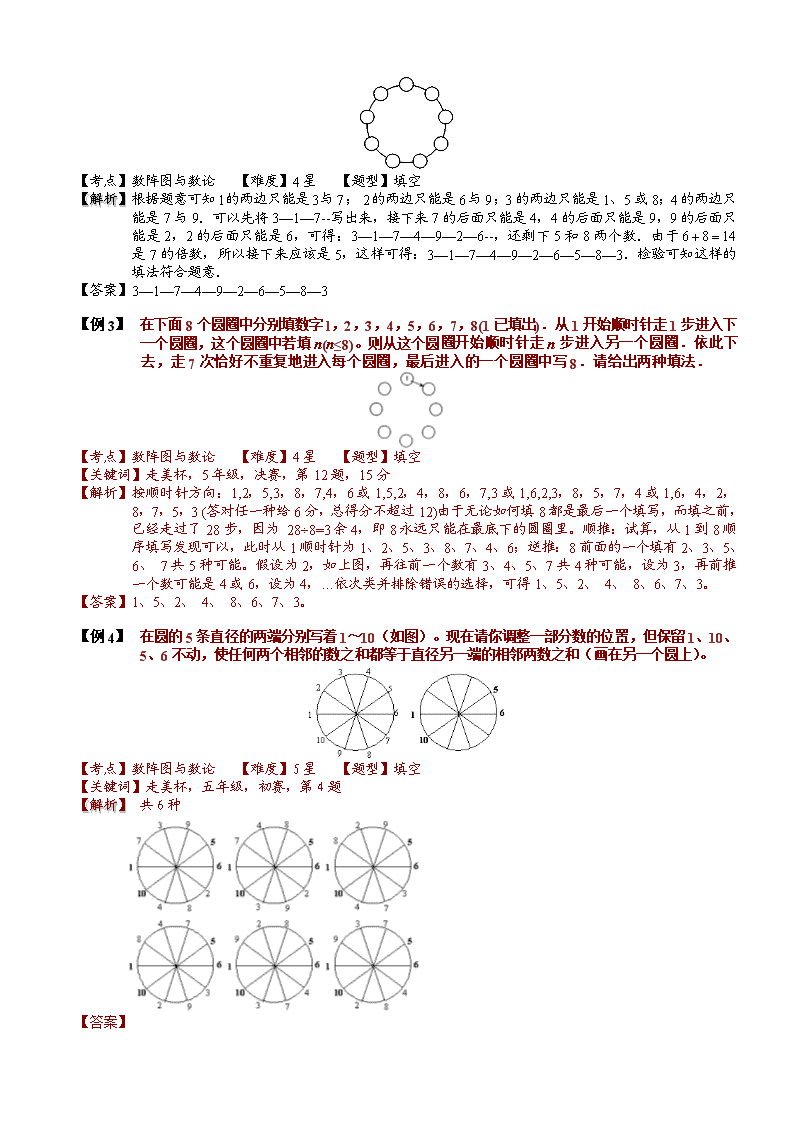例 2】 将填入下图的○中，使得任意两个相邻的数之和都不是，，的倍数．‎ ‎【考点】数阵图与数论 【难度】4星 【题型】填空 ‎ 【解析】 根据题意可知的两边只能是与；的两边只能是与；3的两边只能是1、5或8；4的两边只能是7与9．可以先将3—1—7--写出来，接下来7的后面只能是4，4的后面只能是9，9的后面只能是2，2的后面只能是6，可得：3—1—7—4—9—2—6--，还剩下5和8两个数．由于是7的倍数，所以接下来应该是5，这样可得：3—1—7—4—9—2—6—5—8—3．检验可知这样的填法符合题意．‎ ‎【答案】3—1—7—4—9—2—6—5—8—3‎ 【例 1】 在下面8个圆圈中分别填数字l，2，3，4，5，6，7，8(1已填出)．从1开始顺时针走1步进入下一个圆圈，这个圆圈中若填n(n≤8)。则从这个圆圈开始顺时针走n步进入另一个圆圈．依此下去，走7次恰好不重复地进入每个圆圈，最后进入的一个圆圈中写8．请给出两种填法．‎ ‎【考点】数阵图与数论 【难度】4星 【题型】填空 ‎【关键词】走美杯，5年级，决赛，第12题，15分 【解析】 按顺时针方向：1,2，5,3，8，7,4，6或1,5,2，4，8，6，7,3或1,6,2,3，8，5，7，4或1,6，4，2，8，7，5，3 (答对任一种给6分，总得分不超过12)由于无论如何填8都是最后一个填写，而填之前，已经走过了28步，因为 28÷8=3余4，即8永远只能在最底下的圆圈里。顺推：试算，从1到8顺序填写发现可以，此时从1顺时针为1、2、5、3、8、7、4、6；逆推：8前面的一个填有2、3、5、6、 7共5种可能。假设为2，如上图，再往前一个数有3、4、5、7共4种可能，设为3，再前推一个数可能是4或6，设为4，…依次类并排除错误的选择，可得1、5、2、 4、 8、6、7、3。‎ ‎【答案】1、5、2、 4、 8、6、7、3。‎ 【例 2】 在圆的5条直径的两端分别写着1～10（如图）。现在请你调整一部分数的位置，但保留1、10、5、6不动，使任何两个相邻的数之和都等于直径另一端的相邻两数之和（画在另一个圆上）。‎ ‎【考点】数阵图与数论 【难度】5星 【题型】填空 ‎【关键词】走美杯，五年级，初赛，第4题 【解析】 共6种 ‎【答案】‎ 【例 1】 图中是一个边长为1的正六边形，它被分成六个小三角形．将4、6、8、10、12、14、16各一个填入7个圆圈之中．相邻的两个小正三角形可以组成6个菱形，把每个菱形的四个顶点上的数相加，填在菱形的中心A、B、C、D、E、F位置上（例如：）．已知A、B、C、D、E、F依次分别能被2、3、4、5、6、7整除，那么___________． ‎ ‎【考点】数阵图与数论 【难度】5星 【题型】填空 ‎【关键词】迎春杯，六年级，初赛，第12题 【解析】 先考虑菱形顶点的和为3、6的倍数，7个数被3除的余数分别为1、0、2、1、0、2、1，可以得到中间数g=8或14，同样分析5的倍数，7的倍数，得到具体的填法（如图），a´g´d=4´8´10=320评注：采用余数分析法，找到关键数的填法。‎ ‎ ‎ ‎【答案】‎ 【例 2】 在如图所示的圆圈中各填入一个自然数，使每条线段两端的两个数的差都不能被3整除。请问这样的填法存在吗?如存在，请给出一种填法；如不存在，请说明理由。‎ ‎【考点】数阵图与数论 【难度】4星 【题型】填空 ‎【关键词】希望杯，六年级，二试，第18题，10分 【解析】 图中共有4个不同的数，每个数除以3的余数只可能有0、1、2三种，根据抽屉原理可知，这4个数中必然至少存在一对同余的数，那么这两个数的差必然为3的倍数，故不存在这样的填法。‎ ‎【答案】不存在这样的填法 【例 3】 如图被分成四个小三角形，请在每个小三角形里各填入一个数，满足下面两个要求：(1)任何两个有公共边的三角形里的数都互为倒数(如：和是互为倒数)；(2)四个小三角形里的数字的乘积等于225。 则中问小三角形里的数是 ‎【考点】数阵图与数论 【难度】3星 【题型】填空 ‎【关键词】希望杯，六年级，初赛，第3题，6分 【解析】 四个小三角形共三对相邻三角形，这三对的积都是1，所以将这三对数乘起来，得到的积还是1,但其中中间的数被乘了3次,如果只乘1次那么积为225，所以中间的数是.‎ ‎【答案】‎ 【例 1】 ‎（2010年第8届走美杯3年级初赛第8题）年是虎年，请把这个数不重复的填入虎额上的“王”字中，使三行，一列的和都等于 ‎【考点】复合型数阵图 【难度】5星 【题型】填空 ‎ ‎【关键词】走美杯，3年级，初赛 【解析】 三个答案均可 三个交叉点数的和是：，只能是。剩下通过整数分拆即可得到如图的三种实质不同的答案 ‎【答案】‎ 【例 2】 将1～9这9个数字填入下图的9个圆圈内，使得每条线段两端上的两个数字之和各不相同（即可得到12个不同的和）。‎ ‎【考点】数阵图与数论 【难度】5星 【题型】填空 ‎【关键词】走美杯，3年级，决赛，第4题，8分 【解析】 答案不唯一。例如：‎ ‎【答案】‎ 【例 1】 在棋盘中，如果两个方格有公共点，就称为相邻的。右图中A有3个相邻的方格，而B有8个相邻的方格。图中每一个奇数表示与它相邻的方格中，偶数的个数（如3表示相邻的方格中有3个偶数），每个偶数表示与它相邻的方格中，奇数的个数（如4表示相邻的方格中有4个奇数）。请在下面的4×4的棋盘中填数（至少有一个奇数），满足上面的要求。‎ ‎【考点】数阵图与数论 【难度】5星 【题型】填空 ‎【关键词】走美杯，4年级，决赛，第12题，12分 【解析】 如右图 ‎【答案】答案不唯一 【例 2】 在右图所示的55方格表的空白处填入适当的自然数，使得每行、每列、每条对角线上的数的和都是30。要求：填入的数只有两种不同的大小，且一种是另一种的2倍。‎ ‎【考点】复合型数阵图 【难度】5星 【题型】填空 ‎【关键词】走美杯，3年级，决赛，第12题，12分 【解析】 提示：设填入的较小的数为a，则较大的数为‎2a。第一行要填的两数之和为16，最后一列要填的两数之和为8，由此知第一行填入了两个较大的数，第一列填入了两个较小的数。较大的数为16÷2=8，较小的数为8÷24。得到下图。‎ ‎ 其余数容易填入。‎ ‎【答案】‎ 【例 1】 请在右图所示4×4的正方形的每个格子中填入l或2或3，使得每个2×2的正方形中所填4个数的和各不相同。 ‎ ‎【考点】数阵图与数论 【难度】4星 【题型】填空 ‎【关键词】走美杯，4年级，决赛，第10题，12分 【解析】 ‎【答案】答案不唯一 【例 2】 请在8×8表格的每个格子中填人1或2或3，使得每行、每列所填数的和各不相同。‎ ‎【考点】数阵图与数论 【难度】4星 【题型】填空 ‎【关键词】走美杯，决赛，5年级，决赛，第12题，10分 【解析】 答案不唯一 ‎【答案】‎ ‎ ‎ 【例 1】 在8×8表格的每格中各填入一个数，使得任何一个5×5正方形中25个数的平均数都大于3，而整个8×8表格中64个数的平均数都小于2．‎ ‎【考点】 【难度】星 【题型】填空 ‎【关键词】走美杯，5年级，决赛，第12题，15分 【解析】 如图所示，根据题意，在任何一个任何一个5×5正方形中的总和应该大于75，而整个的数之和要小于128，其中粗线格部分的在所有的5×5的正方形里都存在，我们要让它尽可能的大，同时让外边的尽可能的小，则外面的60个方格最小和为60，中间四个方格，应该小于68。在每一个5×5的正方形内除去这4个，所有之和为21，则中间四个数之和应该大于54，即只要中间四个数的和在54到68之间即可。如14+14+14+14.其他方格里均填写1.‎ ‎【答案】答案不唯一可以在粗线格里添，其余方格添 【例 2】 将最小的个合数填到图中所示表格的个空格中，要求满足以下条件：‎ ‎（1）填入的数能被它所在列的第一个数整除 ‎（2）最后一行中每个数都比它上面那一格中的数大。那么，最后一行中个数的和最小是 ‎ ‎【考点】数阵图与数论 【难度】4星 【题型】填空 ‎ 【解析】 最小的个合数分别是，，，，，，，，，．这个合数当中和一定是在的下面，其中15在最后一行；、、、一定是在和下面，其中14一定在2的下面；剩下的、、、在或下面，其中一定在的下面，对和所在的列和和所在的列分别讨论．、、、，这四个数中最大的数一定在最后一行，最小的数一定在第二行，所以和所在的列中最后一行的数的和最小是，当、在下面，和在下面时成立；、、、，这四个数中最大的数一定在最后一行，最小的数一定在第二行，所以和所在的列中最后一行的数的和最小是，当和在下面，和在下面时成立．所以最后一行的个数的和最小是。‎ ‎【答案】‎ 【例 1】 老师给前来参加“迎春晚会”的31位同学发放编号：1，2，……，31．如果有两位同学的编号的乘积是他们编号和的倍数，则称这两位同学是“好朋友”．从这31位同学中至少需要选出 人，才能保证在选出的人中一定可以找到两位同学是“好朋友”．‎ ‎【考点】数阵图与数论 【难度】6星 【题型】填空 ‎【关键词】迎春杯，高年级，决赛，15题 【解析】 如果两个编号的同学是“好朋友”，那么，则．‎ 时满足条件的有；‎ 时满足条件的有；‎ 时满足条件的有、；‎ 时满足条件的有；‎ 时满足条件的有、、；‎ 时满足条件的有；‎ 时满足条件的有；‎ 时满足条件的有、；‎ 则全部同学相互之间的关系网如图(其余名学生未列)：‎ 关系网图可分为不关联的部分，其中包含个人的部分最多可以选出名互不是“好朋友”的同学，包含个人的两个部分各可选出人，以保证互不是“好朋友”，加上未列出的16人，所以人中最多可以选出人互不是“好朋友”，此时只要再选出一人，即可保证选出的人当中有两位同学是“好朋友”，所以至少应该选出人．‎ 小结：本题容易忽略掉21和28这一对“好朋友”．‎ ‎【答案】人