各地小升初数学模拟试卷及解析广东省揭阳市 14页

小升初数学模拟试卷及解析 广东省揭阳市 一、填空题（每空1分，共21分）‎ ‎1．把2574400“四舍五入”到万位的近似数记作　　　　　　万；把2872790000“四舍五入”到亿位的近似数记作　　　　　　亿．‎ ‎　‎ ‎2．一个数由8个1和2个组成，这个数是　　　　　　，它的倒数是　　　　　　．‎ ‎　‎ ‎3．把2.83扩大100倍后是　　　　　　；把54缩小　　　　　　倍后是0.054．‎ ‎　‎ ‎4．把一根3米长的铁丝平均分成5段，每一段长是这根铁丝长的　　　　　　，每段长　　　　　　米．‎ ‎　‎ ‎5．3千克50克=　　　　　　千克，3分40秒=　　　　　　秒．‎ ‎　[来源:学科网]‎ ‎6．0.75=12÷　　　　　　=　　　　　　：12=．‎ ‎　‎ ‎7．右边是一个等腰三角形，已知∠1=100°，那么∠2=　　　　　　，∠3=　　　　　　．‎ ‎　‎ ‎8．期末考试中，李明语文得了87分，自然得了82分，语文、数学、自然三科平均成绩是88分．那么他的三科总分是　　　　　　分，数学得了　　　　　　分．‎ ‎　‎ ‎9．36和48的最大公约数是　　　　　　，最小公倍数是　　　　　　．‎ ‎　‎ ‎10．如果2x：1.5=4，那么x=　　　　　　；如果：=x：，那么x=　　　　　　．‎ ‎　‎ ‎　‎ 二、判断题（对的画“√”，错的画“×”，每小题2分，共10分）‎ ‎11．所有的自然数不是质数就是合数．　　　　　　．（判断对错）‎ ‎　‎ ‎12．6个与4个0.1的和是1．　　　　　　．（判断对错）‎ ‎　‎ ‎13．半径的长短决定圆的大小．　　　　　　．（判断对错）‎ ‎　‎ ‎14．四条边都相等的四边形都是正方形．　　　　　　．（判断对错）‎ ‎　‎ ‎15．边长与直径相等的正方形和圆，正方形的面积比圆的面积小．　　　　　　．（判断对错）‎ ‎　‎ ‎　‎ 三、选择题．（把正确答案的序号填在括号里，每小题2分，共10分）‎ ‎16．表示两个比相等的式子叫做（　　）‎ ‎　 A． 比例 B． 比值 C． 方程 ‎　‎ ‎17．利率一定，本金和利息（　　）‎ ‎　 A． 不成比例 B． 成正比例 C． 成反比例 ‎　‎ ‎18．等边三角形是（　　）‎ ‎　 A． 锐角三角形 B． 直角三角形 C． 钝角三角形 ‎　‎ ‎19．下面图形中，不一定是轴对称图形的是（　　）‎ ‎　 A． 圆 B． 梯形 C． 等腰三角形 ‎　‎ ‎20．圆柱和侧面积展开图是个（　　）‎ ‎　 A． 圆形 B． 长方形 ‎　 C． 长方形或正方形 　 　‎ ‎　‎ ‎　‎ 四、解答题（共1小题，满分12分）‎ ‎21．（12分）（2015•揭阳模拟）计算 ‎1735+450÷18×15； ‎ ‎0.51÷+9.49×3.5；‎ ‎2.04×[1÷（2.1﹣2.09）]；‎ ‎．‎ ‎　‎ ‎　‎ 五、列式计算（每小题6分，共12分）‎ ‎22．一个数的比这个数的20%多4，这个数是多少？‎ ‎　‎ ‎23．求图中阴影部分的面积．（图中单位：厘米）‎ ‎　‎ ‎　‎ 六、应用题（每小题8分，共16分）‎ ‎24．一种农用盐水用盐和水按1：50配制而成．‎ ‎（1）要配制这种盐水255千克，需要盐和水各多少千克？‎ ‎（2）桶内备有300千克水，要配制这种盐水，应在水中放多少千克盐？‎ ‎　‎ ‎25．一个圆柱形油桶的底面积为12.56平方分米，容积是62.8升．如果要制造这样一个无盖油桶，至少需要铁皮多少平方分米？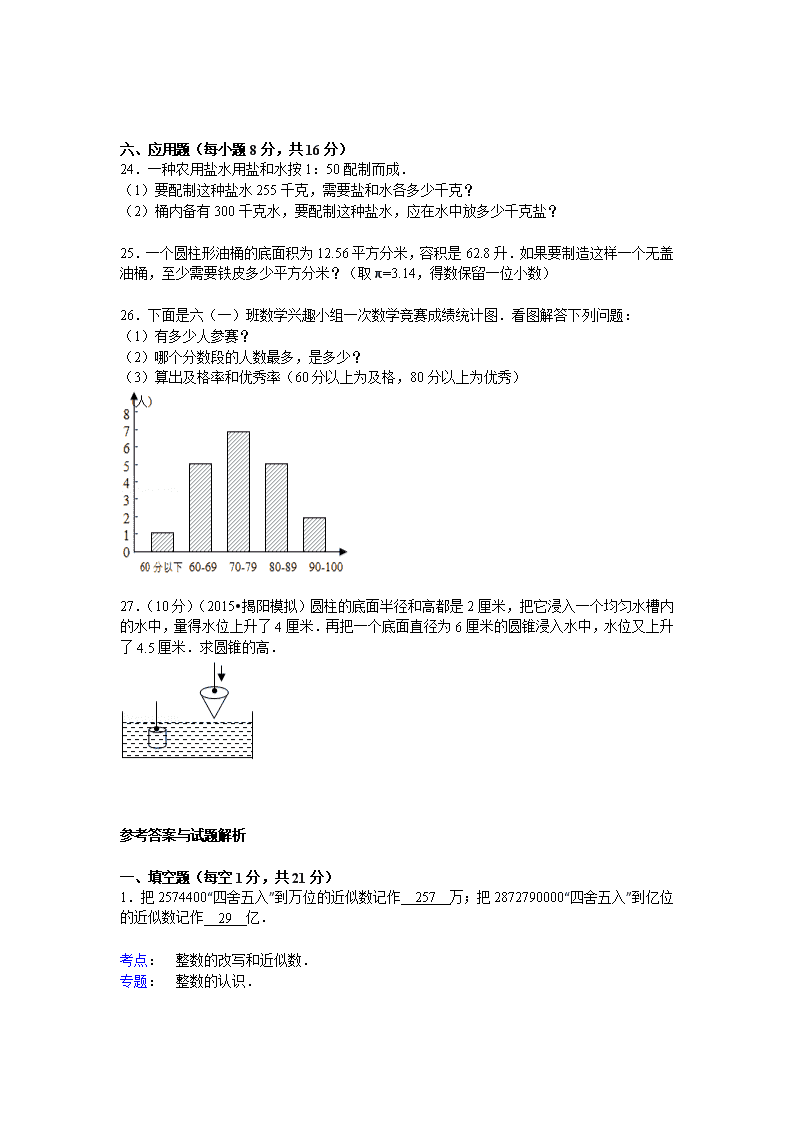（取π=3.14，得数保留一位小数）‎ ‎　‎ ‎26．下面是六（一）班数学兴趣小组一次数学竞赛成绩统计图．看图解答下列问题：‎ ‎（1）有多少人参赛？‎ ‎（2）哪个分数段的人数最多，是多少？‎ ‎（3）算出及格率和优秀率（60分以上为及格，80分以上为优秀）‎ ‎　‎ ‎27．（10分）（2015•揭阳模拟）圆柱的底面半径和高都是2厘米，把它浸入一个均匀水槽内的水中，量得水位上升了4厘米．再把一个底面直径为6厘米的圆锥浸入水中，水位又上升了4.5厘米．求圆锥的高．‎ ‎　‎ ‎　‎ 参考答案与试题解析 ‎　‎ 一、填空题（每空1分，共21分）‎ ‎1．把2574400“四舍五入”到万位的近似数记作　257　万；把2872790000“四舍五入”到亿位的近似数记作　29　亿．‎ 考点： 整数的改写和近似数． ‎ 专题： 整数的认识．‎ 分析： 把2574400改写成用“万”作单位的数，四舍五入到万位，看千位上的数，运用“四舍五入法”解答；‎ 把2872790000“四舍五入”到亿位要看千万位，千万位上的数满5时进1，不满5时舍去，解答即可．‎ 解答： 解：2574400≈257万；‎ ‎2872790000≈29亿 故答案为：257；29．‎ 点评： 本题主要考查整数的改写和求近似数，注意带计数单位．‎ ‎　‎ ‎2．一个数由8个1和2个组成，这个数是　　，它的倒数是　　．‎ 考点： 分数的加法和减法；倒数的认识． ‎ 专题： 运算顺序及法则．‎ 分析： 8个1是8，2个是，把它们相加可知这个数是多少，再除1可得它的倒数，据此解答．‎ 解答： 解：8×1+2×=8‎ ‎1÷8=‎ 答：这个数是8，它的倒数是．‎ 故答案为：8，．‎ 点评： 此题主要考查了学生对分数的组成和倒数知识的掌握．‎ ‎　‎ ‎3．把2.83扩大100倍后是　283　；把54缩小　1000　倍后是0.054．‎ 考点： 小数点位置的移动与小数大小的变化规律． ‎ 专题： 小数的认识．‎ 分析： （1）把2.83扩大100倍，只要把这个数的小数点向右移动2位即可；‎ ‎（2）由54变成0.054，是小数点向左移动了3位，此数就缩小了1000倍；据此解答．‎ 解答： 解：把2.83扩大100倍后是 283；把54缩小 1000倍后是0.054；‎ 故答案为：283，1000．‎ 点评： 此题主要考查小数点位置移动引起数的大小变化规律：一个数的小数点向右（向左）移动一位、两位、三位…，这个数就比原来扩大（缩小）10倍、100倍、1000倍…，反之也成立．‎ ‎　‎ ‎4．把一根3米长的铁丝平均分成5段，每一段长是这根铁丝长的　　，每段长　或0.6　米．[来源:学。科。网Z。X。X。K]‎ 考点： 分数的意义、读写及分类；分数除法． ‎ 专题： 文字题．‎ 分析： （1）求每一段长是这根铁丝长的几分之几，就是把这根3米长的铁丝看作单位“1”，平均分为5份，求一份是这根铁丝长的几分之几，用1÷5解答；‎ ‎（2）求每段长长多少米，用这根铁丝长除以段数即可．‎ 解答： 解：（1）每一段长是这根铁丝长的：1÷5=；‎ ‎（2）3÷5=或0.6（米）；‎ 故答案为：，或0.6．‎ 点评： 本题主要考查分数的意义，注意找准单位“1”，平均分了几份．‎ ‎　‎ ‎5．3千克50克=　3.05　千克，3分40秒=　220　秒．‎ 考点： 质量的单位换算；时、分、秒及其关系、单位换算与计算． ‎ 专题： 质量、时间、人民币单位．‎ 分析： 把3千克50克换算为千克，先把50克换算为千克，用50除以进率1000，然后加上3；‎ 把3分20秒换算成秒，先把3分换算成秒，用3乘进率60，得数再加上20．‎ 解答： 解：3千克50克=3.05千克，3分40秒=220秒；‎ 故答案为：3.05，220．‎ 点评： 此题考查名数的换算，把高级单位的名数换算成低级单位的名数，就乘单位间的进率，把低级单位的名数换算成高级单位的名数，就除以单位间的进率．‎ ‎　‎ ‎6．0.75=12÷　16　=　9　：12=．‎ 考点： 比与分数、除法的关系；小数、分数和百分数之间的关系及其转化． ‎ 专题： 综合填空题．‎ 分析： 解答此题的突破口是0.75，把0.75化成分数是；将此分数化简是，根据分数与除法的关系=3÷4，再根据商不变的性质被除数、除数都乘4就是12÷16；根据比与分数的关系=3：4，再根据比的基本性质比的前、后项都乘3就是9：12．‎ 解答： 解：0.75=12÷16=9：12=．‎ 故答案为：16，9，100．‎ 点评： 此题主要是考查除法、小数、分数、比之间的关系及转化．利用它们之间的关系和性质进行转化即可．‎ ‎　‎ ‎7．右边是一个等腰三角形，已知∠1=100°，那么∠2=　80°　，∠3=　50°　．‎ 考点： 三角形的内角和；等腰三角形与等边三角形． ‎ 分析： （1）因为∠1和∠2的和是平角，所以∠2=180°﹣∠1，又∠1=100°，因此∠2很容易得出；‎ ‎（2）因为△ABC是等腰三角形，利用三角形的内角和，即可求出∠3的度数．‎ 解答： 解：（1）∠2=180°﹣∠1=180°﹣100°=80°；‎ ‎（2）因为△ABC是等腰三角形，‎ 所以∠3=（180°﹣∠2）÷2，‎ ‎=（180°﹣80°）÷2，‎ ‎=50°．‎ 故答案为：80°，50°．‎ 点评： 此题考查了平角的概念、等腰三角形的特点，以及三角形的内角和等知识．‎ ‎　‎ ‎8．期末考试中，李明语文得了87分，自然得了82分，语文、数学、自然三科平均成绩是88分．那么他的三科总分是　264　分，数学得了　95　分．‎ 考点： 平均数的含义及求平均数的方法． ‎ 专题： 平均数问题．‎ 分析： 根据语文、数学、自然三科平均成绩是88分，知道语文、数学、自然三科的总分是88×3分，用语文、数学、自然三科的总分减去语文、自然的得分，就是数学的得分．‎ 解答： 解：88×3=264（分），‎ ‎264﹣87﹣82‎ ‎=264﹣169‎ ‎=95（分），‎ 答：数学得了95分．‎ 故答案为：264，95．‎ 点评： 本题考查了平均数的含义及求平均数的方法的实际应用，知识点是：总数量÷份数=平均数．‎ ‎　‎ ‎9．36和48的最大公约数是　12　，最小公倍数是　144　．‎ 考点： 求几个数的最大公因数的方法；求几个数的最小公倍数的方法． [来源:Z。xx。k.Com]‎ 专题： 数的整除．‎ 分析： 先把36和48分解质因数，再根据求最大公因数也就是这几个数的公有质因数的连乘积，最小公倍数是公有质因数与独有质因数的连乘积，由此解决问题即可．‎ 解答： 解：36=2×2×3×3，‎ ‎48=2×2×2×2×3，‎ 所以36和48的最大公因数是：2×2×3=12，‎ 最小公倍数是：2×2×3×3×2×2×3=144；‎ 故答案为：12，144．‎ 点评： 此题主要考查求两个数的最大公因数与最小公倍数的方法：两个数的公有质因数连乘积是最大公因数，两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数；数字大的可以用短除法解答．‎ ‎　‎ ‎10．如果2x：1.5=4，那么x=　3　；如果：=x：，那么x=　　．‎ 考点： 解比例． ‎ 专题： 比和比例．‎ 分析： （1）根据比例基本性质，两内项之积等于两外项之积，化简方程，再依据等式的性质，方程两边同时除以2求解；‎ ‎（2）根据比例基本性质，两内项之积等于两外项之积，化简方程，再依据等式的性质，方程两边同时除以求解．‎ 解答： 解：（1）2x：1.5=4‎ ‎ 2x=1.5×4‎ ‎ 2x÷2=6÷2‎ ‎ x=3‎ ‎（2）：=x：‎ x=×‎ x÷=×÷‎ ‎ x=‎ 故答案为：3，．‎ 点评： 本题主要考查学生依据等式的性质以及比例的基本性质解方程的能力，解方程时注意对齐等号；知识点：比例基本的性质是：两内项之积等于两外项之积．‎ ‎　‎ 二、判断题（对的画“√”，错的画“×”，每小题2分，共10分）‎ ‎11．所有的自然数不是质数就是合数．　×　．（判断对错）‎ 考点： 合数与质数． ‎ 专题： 整数的认识．‎ 分析： 根据质数与合数的意义：一个自然数，如果只有1和它本身两个因数，这样的数叫做质数；一个自然数，如果除了1和它本身还有别的因数，这样的数叫做合数．1既不是质数也不是合数．‎ 解答： 解：根据分析：质数与合数是按照一个自然数的因数的个数的多少进行分类，因为1只有一个因数是它本身，所以1既不是质数也不是合数．‎ 因此所有的自然数不是质数就是合数．这种说法是错误的．‎ 故答案为：错误．‎ 点评： 此题考查的目的是理解质数与合数的意义，明确：质数与合数是按照一个自然数的因数的个数的多少进行分类．‎ ‎　‎ ‎12．6个与4个0.1的和是1．　√　．（判断对错）‎ 考点： 小数的加法和减法． ‎ 专题： 运算顺序及法则．‎ 分析： 6个是×6，4个0.1是0.1×4，然后相加求出和再解答．‎ 解答： 解：×6+0.1×4‎ ‎=0.6+0.4‎ ‎=1．‎ 故答案为：√．‎ 点评： 本题关键是求出结果，然后再判断．‎ ‎　‎ ‎13．半径的长短决定圆的大小．　√　．（判断对错）‎ 考点： 圆的认识与圆周率． ‎ 专题： 压轴题．‎ 分析： 根据“圆心决定圆的位置，半径决定圆的大小”进行判断即可．‎ 解答： 解：因为圆心决定圆的位置，半径决定圆的大小；所以得出：半径的长短决定圆的大小，说法正确；‎ 故答案为：正确．‎ 点评： 此题考查了圆的特征．‎ ‎　‎ ‎14．四条边都相等的四边形都是正方形．　错误　．（判断对错）‎ 考点： 正方形的特征及性质． ‎ 专题： 平面图形的认识与计算．‎ 分析： 根据正方形的含义：有一组邻边相等且有一个角是直角的平行四边形，叫正方形，即正方形四条边都相等，四个角都是90度；进而进行判断即可．‎ 解答： 解：根据正方形含义可知：四边形的四条边相等，但角不一定是90°，所以四条边相等的四边形，都是正方形，说法错误；‎ 故答案为：错误．‎ 点评： 此题应根据正方形的意义进行解答．‎ ‎　‎ ‎15．边长与直径相等的正方形和圆，正方形的面积比圆的面积小．　×　．（判断对错）‎ 考点： 长方形、正方形的面积；圆、圆环的面积． ‎ 专题： 平面图形的认识与计算．‎ 分析： 圆的面积=πr2，正方形的面积=a2，可以假设出圆的半径，分别代入公式求出其面积，即可进行判断．‎ 解答： 解：假设圆的半径为r，‎ 则圆的面积=πr2，‎ 正方形的边长=2r，‎ 则正方形的面积=2r×2r=4r2，‎ 又因4r2＞πr2，‎ 所以一个圆的直径和一个正方形的边长相等，那么正方形的面积一定大于圆的面积．‎ 故答案为：×．‎ 点评： 此题主要考查圆和正方形的面积的计算方法的灵活应用．‎ ‎　‎ 三、选择题．（把正确答案的序号填在括号里，每小题2分，共10分）‎ ‎16．表示两个比相等的式子叫做（　　）‎ ‎　 A． 比例 B． 比值 C． 方程 考点： 比例的意义和基本性质． ‎ 专题： 比和比例．‎ 分析： 用比例的意义：表示两个比相等的式子叫做比例，直接选出答案即可．‎ 解答： 解：比例的意义是：表示两个比相等的式子叫做比例，‎ 故选：A．‎ 点评： 此题主要考查比例的定义的理解和灵活应用．‎ ‎　‎ ‎17．利率一定，本金和利息（　　）‎ ‎　 A． 不成比例 B． 成正比例 C． 成反比例 考点： 辨识成正比例的量与成反比例的量． ‎ 专题： 比和比例．‎ 分析： 判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．‎ 解答： 解：因为：本金×利率=利息，即本金÷利息=利率（一定），商一定，所以本金和利息成正比例；‎ 故选：B．‎ 点评： 此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．‎ ‎　‎ ‎18．等边三角形是（　　）‎ ‎　 A． 锐角三角形 B． 直角三角形 C． 钝角三角形 考点： 等腰三角形与等边三角形；三角形的分类． ‎ 专题： 压轴题．‎ 分析： 根据等边三角形的性质，等边三角形的三个角都相等，再由三角形的三个内角的和是180°，因此可知等边三角形每个内角的度数，再结合三角形按角分类的方法，就可以判断．‎ 解答： 解：根据等边三角形的性质可知，等边三角形的三个内角度数相等，‎ 因为三角形的三个内角的和是180°，‎ 所以每个角的度数都是：180°÷3=60°，‎ 又因为三个角都是锐角的三角形叫做锐角三角形，‎ 因此等边三角形是锐角三角形．‎ 故选：A 点评： 本题考查了等边三角形的性质，以及三角形按角来分类的方法．‎ ‎　‎ ‎19．下面图形中，不一定是轴对称图形的是（　　）‎ ‎　 A． 圆 B． 梯形 C． 等腰三角形 考点： 轴对称图形的辨识． ‎ 专题： 平面图形的认识与计算．‎ 分析： 根据轴对称图形的意义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴；依次进行判断即可．‎ 解答： 解：根据轴对称图形的意义可知：圆、等腰三角形都是轴对称图形，而梯形不一定是轴对称图形；‎ 故选：B．‎ 点评： 此题考查了轴对称图形的意义，判断轴对称图形的关键是寻找对称轴，看图形对折后两部分是否完全重合．‎ ‎　‎ ‎20．圆柱和侧面积展开图是个（　　）‎ ‎　 A． 圆形 B． 长方形 ‎　 C． 长方形或正方形 　 　‎ 考点： 圆柱的展开图． ‎ 专题： 立体图形的认识与计算．‎ 分析： 由圆柱的侧面展开图的特征知它的侧面展开图为长方形或正方形或平行四边形．‎ 解答： 解：圆柱的侧面展开图为长方形或正方形或平行四边形．‎ 故选：C．‎ 点评： 本题考查了圆柱的侧面展开图，熟练掌握常见立体图形的侧面展开图的特征是解决本题的关键．[来源:学科网]‎ ‎　‎ 四、解答题（共1小题，满分12分）‎ ‎21．（12分）（2015•揭阳模拟）计算 ‎1735+450÷18×15； ‎ ‎0.51÷+9.49×3.5；‎ ‎2.04×[1÷（2.1﹣2.09）]；‎ ‎．‎ 考点： 整数四则混合运算；整数、分数、小数、百分数四则混合运算． ‎ 专题： 运算顺序及法则．‎ 分析： （1）先算除法，再算乘法，最后算加法；‎ ‎（2）根据乘法分配律进行简算；‎ ‎（3）先算减法，再算除法，最后算乘法；‎ ‎（4）先算小括号里面的减法，再算中括号里面的减法，最后算除法．‎ 解答： 解：（1）1735+450÷18×15‎ ‎=1735+25×15‎ ‎=1735+375‎ ‎=2110；‎ ‎（2）0.51÷+9.49×3.5‎ ‎=0.51×3.5+9.49×3.5‎ ‎=（0.51+9.49）×3.5‎ ‎=10×3.5‎ ‎=35；‎ ‎（3）2.04×[1÷（2.1﹣2.09）]‎ ‎=2.04×[1÷0.01]‎ ‎=2.04×100‎ ‎=204；‎ ‎（4）‎ ‎=[1﹣]÷‎ ‎=1÷‎ ‎=．‎ 点评： 考查了运算定律与简便运算，四则混合运算．注意运算顺序和运算法则，灵活运用所学的运算定律简便计算．‎ ‎　‎ 五、列式计算（每小题6分，共12分）‎ ‎22．一个数的比这个数的20%多4，这个数是多少？‎ 考点： 整数、分数、小数、百分数四则混合运算． ‎ 专题： 文字叙述题．‎ 分析： 首先求出这个数的比这个数的20%多几分之几；然后根据分数除法的意义，用4除以它占这个数的分率，求出这个数是多少即可．‎ 解答： 解：4÷（%）‎ ‎=4÷‎ ‎=30‎ 答：这个数是30．‎ 点评： 此题主要考查了整数、分数、百分数四则混合运算的方法，以及分数除法的意义的应用，要熟练掌握，注意运算顺序．‎ ‎　‎ ‎23．求图中阴影部分的面积．（图中单位：厘米）‎ 考点： 组合图形的面积． ‎ 专题： 平面图形的认识与计算．‎ 分析： 图中阴影部分的面积是梯形，已知梯形的上底是4厘米，下底是4+4=8厘米，高是4厘米，据此根据梯形的面积=（上底+下底）×高÷2进行解答即可．‎ 解答： 解：（4+4+4）×4÷2‎ ‎=12×4÷2‎ ‎=24（平方厘米）‎ 答：阴影部分的面积是24平方厘米．‎ 点评： 本题主要考查了学生对梯形面积公式的掌握．‎ ‎　‎ 六、应用题（每小题8分，共16分）‎ ‎24．一种农用盐水用盐和水按1：50配制而成．‎ ‎（1）要配制这种盐水255千克，需要盐和水各多少千克？‎ ‎（2）桶内备有300千克水，要配制这种盐水，应在水中放多少千克盐？‎ 考点： 比的应用． ‎ 专题： 比和比例应用题．‎ 分析： （1）根据盐和水重量的比是1：50，可求出盐和水重量的总份数，要分配的总量是255千克的盐水，进而用按比例分配的方法分别求出盐和水的千克数；‎ ‎（2）根据盐和水重量的比是1：50，要求300千克水盐需放盐的千克数，也就是求300千克里有多少个50，用除法计算．‎ 解答： 解：（1）总份数：1+50=51（份 ），‎ 盐的千克数：255×=5（千克），‎ 水的千克数：255﹣5=250（千克）‎ 答：需盐5千克，水250千克．‎ ‎（2）需放盐的千克数：300÷50=6（千克）；‎ 答：配制这种盐水，应在水中放6千克盐．‎ 点评： 此题主要考查按比例分配应用题的特点：已知两个数的比（或三个数的比），两个数的和（或三个数的和），求这两个数（或三个数），用按比例分配的方法解答求得每一个量．‎ ‎　‎ ‎25．一个圆柱形油桶的底面积为12.56平方分米，容积是62.8升．如果要制造这样一个无盖油桶，至少需要铁皮多少平方分米？（取π=3.14，得数保留一位小数）‎ 考点： 关于圆柱的应用题． ‎ 专题： 立体图形的认识与计算．‎ 分析： 根据圆柱的体积=底面积×高，已知体积和底面积即可求出高；再根据圆的面积s=πr2，先求出求出r2，继而求出半径r，最后根据圆柱的表面积公式解答即可．‎ 解答： 解：62.8升=62.8立方分米 高：62.8÷12.56=5（分米）‎ ‎12.56÷3.14=4（平方分米）‎ ‎4=2×2‎ 底面半径为：2分米 ‎12.56+2×3.14×2×5‎ ‎=12.56+31.4‎ ‎=43.96‎ ‎≈44.0（平方分米）；‎ 答：至少需要铁皮44.0平方分米．‎ 点评： 此题主要考查圆柱的体积、表面积及圆的面积公式的应用，解答关键是先求出圆柱的底面半径和高．‎ ‎　‎ ‎26．下面是六（一）班数学兴趣小组一次数学竞赛成绩统计图．看图解答下列问题：‎ ‎（1）有多少人参赛？‎ ‎（2）哪个分数段的人数最多，是多少？‎ ‎（3）算出及格率和优秀率（60分以上为及格，80分以上为优秀）‎ 考点： 以一当二的条形统计图． ‎ 专题： 统计数据的计算与应用．‎ 分析： （1）把各个分数段的人数相加即可求出参赛的总人数；‎ ‎（2）根据图可知：70﹣79分数点的人数最多，是7人；‎ ‎（3）求及格率和优秀率，根据：及格率=及格人数÷总人数×100%，优秀率=优秀人数÷总人数×100%，由此分别解答即可．‎ 解答： 解：（1）1+5+7+5+2=20（人）‎ 答：有20人参赛．[来源:Zxxk.Com]‎ ‎（2）根据图可知：70﹣79分数点的人数最多，是7人．‎ ‎（3）及格率：（20﹣1）÷20×100%‎ ‎=19÷20×100%‎ ‎=99.5%‎ 优秀率：（5+2）÷20×100%‎ ‎=7÷20×100%‎ ‎=35%‎ 答：及格率是99.5%，优秀率是35%．‎ 点评： 此题是考查如何从条形统计图中获取信息，并根据所获取的信息解决实际问题．‎ ‎　‎ ‎27．（10分）（2015•揭阳模拟）圆柱的底面半径和高都是2厘米，把它浸入一个均匀水槽内的水中，量得水位上升了4厘米．再把一个底面直径为6厘米的圆锥浸入水中，水位又上升了4.5厘米．求圆锥的高．‎ 考点： 探索某些实物体积的测量方法；圆柱的侧面积、表面积和体积；圆锥的体积． ‎ 专题： 立体图形的认识与计算．‎ 分析： 根据圆柱的体积公式得到圆柱的体积，除以水位上升的高度得到水槽的底面积，再用水槽的底面积乘以圆锥浸入水中水位上升的高度，得到圆锥的体积，再根据圆锥的体积公式得到圆锥的高．‎ 解答： 解：3.14×22×2÷4‎ ‎=3.14×4×2÷4‎ ‎=6.28（平方厘米）‎ ‎6.28×4.5×3÷[3.14×（6÷2）2]‎ ‎=3.14×27÷[3.14×9]‎ ‎=3（厘米）‎ 答：圆锥的高是3厘米．‎ 点评： 本题主要考查特殊物体体积的计算方法，将物体放入或取出，水面上升或下降的体积就是物体的体积．‎ ‎　‎