六年级数学下册第6章整理与复习4数学思考课件新人教版 19页

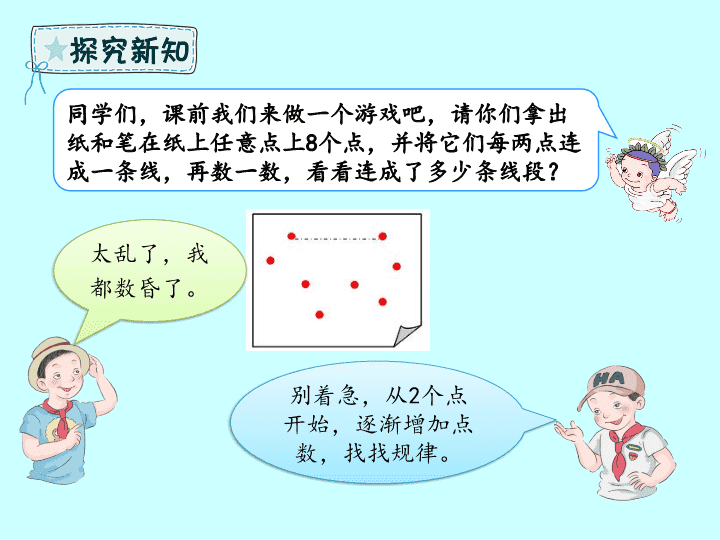
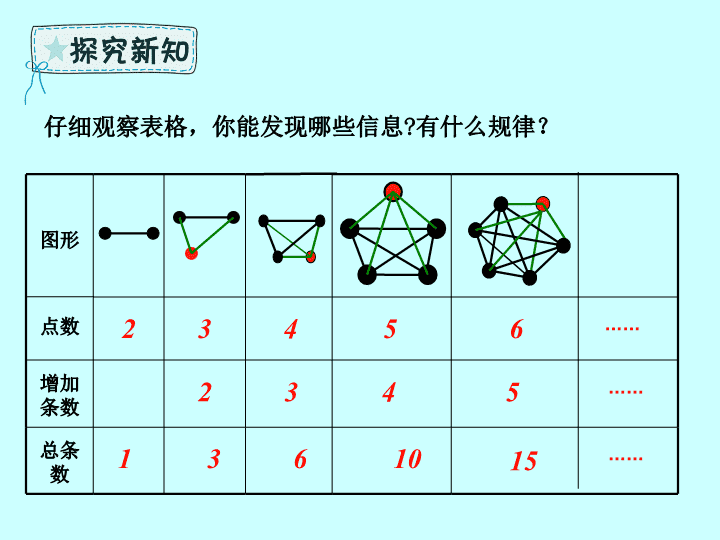
数学思考 6 整理和复习 同学们，课前我们来做一个游戏吧，请你们拿出纸和笔在纸上任意点上 8 个点，并将它们每两点连成一条线，再数一数，看看连成了多少条线段？ 别着急，从 2 个点开始，逐渐增加点数，找找规律。 太乱了，我都数昏了。 图形 点数 增加条数 总条 数 仔细观察表格，你能发现哪些信息 ? 有什么规律？ 2 1 3 2 3 4 3 6 5 4 10 6 5 15 …… …… …… 仔细观察表格，你能发现哪些信息 ? 有什么规律？ 点数 增加条数 总条数 2 1 3 2 1 ＋ 2＝3 （条） 4 3 1 ＋ 2 ＋ 3＝ 6 （条） 5 4 1 ＋ 2 ＋ 3 ＋ 4 ＝ 10 （条） 6 5 1 ＋ 2 ＋ 3 ＋ 4 ＋ 5 ＝ 15 （条） 1. 按照规律， 6 个点能连几条线段？ 8 个点呢？ 1 + 2 + 3 + 4 + 5 + 6 + ... + （点数－ 1 ） = 总条数 点数 ×( 点数 — 1) ÷ 2 = 总条数 点数 × 增加条数 ÷ 2 = 总条数 n ×(n-1) ÷2 即：点数 × （点数 -1 ） ÷2 1 ＋ 2 ＋ 3 ＋ 4 ＋ 5 ＋ 6 ＋ 7 ＝ 28 （条） 8 个点： 12 个点： 1 ＋ 2 ＋ 3 ＋ 4 ＋ 5 ＋ 6 ＋ 7 ＋ 8 ＋ 9 ＋ 10 ＋ 11 ＝ 66 （条） 2. 根据规律，你知道 12 个点、 20 个点能连多少条线段吗？ 20 个点： 1 ＋ 2 ＋ 3 ＋ 4 ＋ 5 ＋ 6 ＋ 7 ＋ 8 ＋ 9 ＋ 10 ＋ 11 ＋ 12 ＋ 13 ＋ 14 ＋ 15 ＋ 16 ＋ 17 ＋ 18 ＋ 19 ＝ 190 （条） 3. 有序思考 2. 画图、枚举 1. 化繁为简 4. 探究规律 同学们，在我们生活中有许多看似复杂的问题，我们都可以尝试从简单问题去思考，逐步找到其中的规律，从而来解决复杂的问题。 寒假过去了， 10 个好朋友见面了，每两位好朋友握手一次，请同学们帮忙算算，他们一共握了多少次手？ 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 （次） 答：一共握了 45 次手。 10 × (10 - 1) ÷ 2 = 45 （次） ( 1 + 9 ) × 9 ÷ 2 = 45 （次） 六年级有三个班，每班有 2 个班长。开班长会时，每次每班只要一个班长参加。第一次到会的有 A 、 B 、 C ；第二次有 B 、 D 、 E ；第三次有 A 、 E 、 F 。请问：哪两位班长是同班的？ 知道的信息： 1. 第一次到会的有 A,B,C ，说明 A,B,C 三位班长不同班。 2. 第二次到会的有 B,D,F ，说明三位班长不同班。 3. 第三次到会的有 A,E,F ，说明三位班长不同班。 用数字“ 1 ” 表示到会，用数字“ 0 ”表示没到会。 A B C D E F 第一次 1 1 1 0 0 0 第二次 0 1 0 1 1 0 第三次 1 0 0 0 1 1 用列表的方法试一试。 A B C D E F 第一次 1 1 1 0 0 0 第二次 0 1 0 1 1 0 第三次 1 0 0 0 1 1 A B C D E F 第一次 1 1 1 0 0 0 第二次 0 1 0 1 1 0 第三次 1 0 0 0 1 1 问题： 1. A 可能和谁是同班？ 2. 请你根据表格继续推理， B 、 C 可能和谁是同班呢？ A B C D E F 第一次 1 1 1 0 0 0 第二次 0 1 0 1 1 0 第三次 1 0 0 0 1 1 A B C D E F 第一次 1 1 1 0 0 0 第二次 0 1 0 1 1 0 第三次 1 0 0 0 1 1 √ √ √ √ √ √ √ × √ √ √ √ √ √ × √ × 列表的方法真简单。 王阿姨、刘阿姨、丁叔叔、李叔叔分别是工人、教师、军人。王阿姨是教师；丁叔叔不是工人；只有刘阿姨和李叔叔的职业相同。请问：他们的职业各是什么？ 问题：你想用什么方法解决这个问题？ 王阿姨 刘阿姨 丁叔叔 李叔叔 工人 教师 军人 × × √ √ √ √ 列表是解决复杂问题的好方法。 （ 1 ）已知 ＋ ＝ 24 ， ＝ ＋ ＋ 。 求 和 的值。 问题： 是什么意思？ ＝ ＋ ＋ 1. 等量代换 ＋ ＝ 24 ＝ 6 ＋ ＝ 24 ＋ ＋ ＝ ＋ ＋ ＝ 18 圈起来的这一步运用了什么数学思想？ （ 2 ） ＋ ＝ 160 ， 是否等于 ？ ＋ ＝ 160 。 ＋ ＝ ＋ ＝ － ＋ ＝ ＋ － 3. 如右图，两条直线相交于点 O 。 ∠1 和 ∠2 、∠ 2 和 ∠3 、∠ 3 和 ∠4 、∠ 4 和 ∠1 ，一共能组成 4 个平角。 （ 1 ）每相邻两个角可以组成一个平角，一共能组成几个平角？ （ 2 ）你能推出 ∠1 ＝ ∠3 吗？ ∠1 ＋ ∠2 ＝ 180° ∠2 ＋ ∠3 ＝ 180° ∠1 ＋ ∠2 ＝ ∠2 ＋ ∠3 ∠3 ∠1 ＝ ＝ －∠2 ∠1 ＋ ∠2 ∠2 ＋ ∠3 －∠2 这节课你有什么收获？ 遇到复杂的问题，可以尝试从简单问题去思考，逐步找到其中的规律，从而来解决复杂的问题。 列表也是解决复杂问题的好方法。 作业 请完成教材第 103 页练习二十二，第 4 题，第 6 题。 xx 小学 x 年级 x 班 xxx