中山市中考数学纪中三鑫第四次模拟试题 4页

‎2017年广东省初中毕业生学业考试纪中三鑫第四次模拟考试 数学试题 ‎ ‎ 一、选择题（本大题共10小题，每小题3分，共30分，每小题均有四个选项，其中只有一项符合题目要求）‎ ‎1、在|﹣2|，0，1，﹣1这四个数中，最大的数是（　　）‎ A．|﹣2| B．0 C．1 D．﹣1‎ ‎2、下列图形中，既是中心对称图形又是轴对称图形的是（　　）‎ A．角 B．等边三角形 C．平行四边形 D．圆 ‎3、计算3a﹣2a的结果正确的是（　　）‎ A．﹣5a B．﹣a C．a D．1‎ ‎4、一个多边形的内角和是1260°，这个多边形的边数是（　　）‎ A．7 B．8 C．9 D．10‎ ‎5、把8a3﹣8a2+2a进行因式分解，结果正确的是（　　）‎ A．2a（4a2﹣4a+1） B．8a2（a﹣1） C．2a（2a﹣1）2 D．2a（2a+1）2‎ ‎6、如图，在平行四边形ABCD中，AC与BD交于点O，下列说法正确的是（　　）‎ A．AC=BD B．AC⊥BD C．AO=CO D．AB=BC ‎7、一个布袋里装有只有颜色不同的5个球，其中3个红球，2个白球．从中任意摸出1个球，记下颜色后放回，搅匀，再任意摸出1个球．摸出的2个球都是红球的概率是（　　）‎ A． B． C． D．‎ ‎8、若一个等腰三角形的两边长分别为2cm和3cm，则该等腰三角形的周长为（　　）cm．‎ A．8 B．7 C．8或7 D．无法确定 ‎9、已知关于x的一元二次方程mx2+2x﹣1=0有两个不相等的实数根，则m的取值范围是（　　）‎ A．m＜﹣1 B．m＞1 C．m＜1且m≠0 D．m＞﹣1且m≠0‎ ‎10、已知二次函数y=ax2+bx+c的图象如图所示，则不正确的是（　　）‎ A．c＞0 B．a+b+c＜0 C．a＜0 D．b＞0‎ 二、填空题（本大题共6小题，每小题4分，共24分）‎ ‎11、已知式子有意义，则x的取值范围是　______　.‎ ‎12、据统计，2016年底LTE网络用户数己达到560 000 000，将560 000 000用科学记数法表示为　___________　．‎ ‎13、如图，在△ABC中，D、E分别是边AB、AC的中点，BC=8，则DE=　__　．‎ ‎14、如图，在半径为5cm的⊙O中，圆心O到弦AB的距离为3cm，则弦AB的长是　__　．‎ ‎15、不等式组的解集是　____　．‎ ‎16、如图，已知△ABC为等腰直角三角形，∠BAC=90°，AC=2，以点C为圆心，1为半径作圆，点P为⊙C上一动点，连结AP，并绕点A顺时针旋转90°得到AP′，连结CP′，则CP′的取值范围是　_______　．‎ 第14题图 第16题图 ‎ 第13题图 三、解答题（一）（本大题共3小题，每小题6分，共18分）‎ ‎17、计算：（π﹣3.14）0﹣|sin60°﹣4|+（）﹣1．‎ ‎18、先化简，再求值：，其中x=+1．‎ ‎19、如图，在△ABC中，延长BC至D，∠A=60°，∠B=45°．‎ ‎（1）过点C作直线CE∥AB（尺规作图，不写作法，保留作图痕迹）；‎ ‎（2）求∠ACD的度数．‎ 四、解答题（二）（本大题共3小题，每小题7分，共21分）‎ ‎20、罗三妹山位于中山市三乡镇雍陌村，中山温泉宾馆北。因孝女罗三妹的传说而得名，更因为邓小平同志登山时所留下“不走回头路”的名言而名闻遐迩。我校综合实践活动小组要测量“主山峰”的高度，先在罗山妹山对面的A处测得“峰顶”N的仰角为45°，此时，他们刚好与峰底D在同一水平线上．然后沿着坡度为30°的斜坡正对着“主山峰”前行700米，到达B处，再测得“峰顶”N的仰角为60°，如图，根据以上条件求出“主山峰”的高度？（测角仪的高度忽略不计，结果精确到1米，参考数据：≈1.4，≈1.7）．‎ ‎21、某商场搞换季促销活动，若每件羽绒衫按原售价的5折销售可赚50元，按原售价的6折销售可赚80元．问：‎ ‎（1）每件羽绒衫的原售价和成本价各是多少？‎ ‎（2）为保证盈利不低于20元，最多打几折？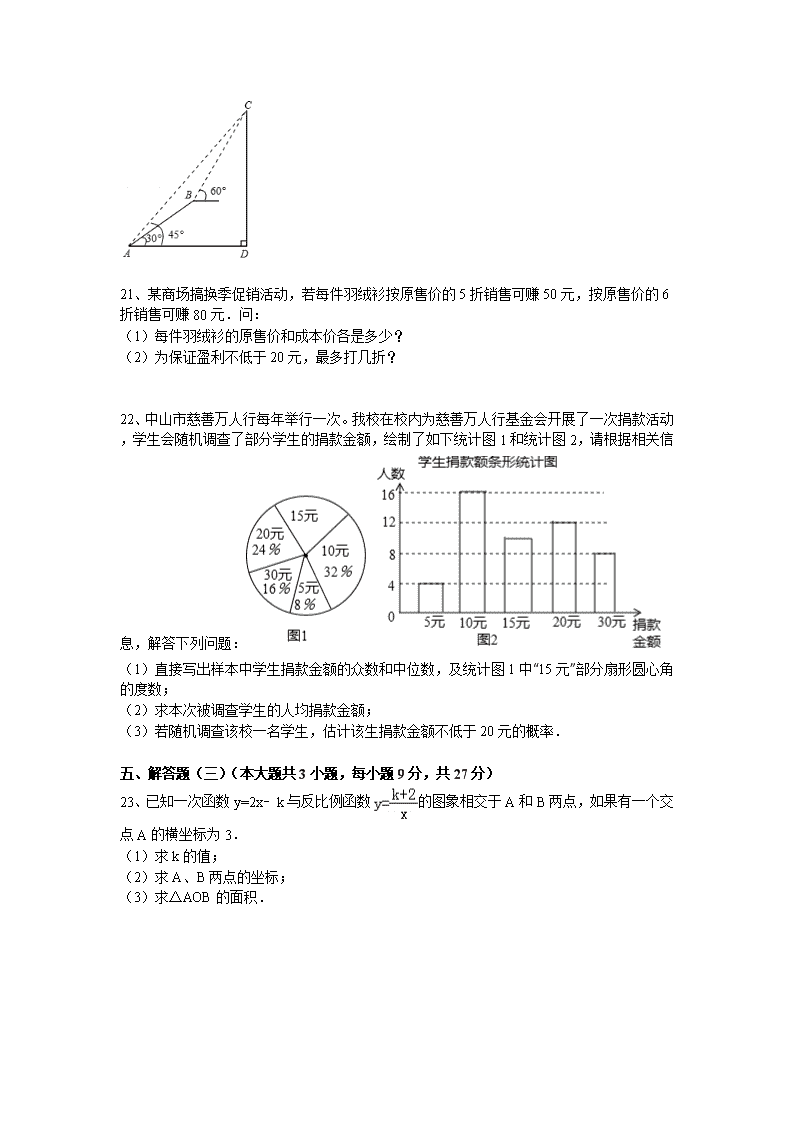‎ ‎22、中山市慈善万人行每年举行一次。我校在校内为慈善万人行基金会开展了一次捐款活动，学生会随机调查了部分学生的捐款金额，绘制了如下统计图1和统计图2，请根据相关信息，解答下列问题：‎ ‎（1）直接写出样本中学生捐款金额的众数和中位数，及统计图1中“15元”部分扇形圆心角的度数；‎ ‎（2）求本次被调查学生的人均捐款金额；‎ ‎（3）若随机调查该校一名学生，估计该生捐款金额不低于20元的概率．‎ 五、解答题（三）（本大题共3小题，每小题9分，共27分）‎ ‎23、已知一次函数y=2x﹣k与反比例函数的图象相交于A和B两点，如果有一个交点A的横坐标为3．‎ ‎（1）求k的值；‎ ‎（2）求A、B两点的坐标；‎ ‎（3）求△AOB的面积．‎ ‎24、如图，⊙O是△ABC的外接圆，AC是直径，过点O作OD⊥AB于点D，延长OD交⊙O于点P，过点P作PE⊥AC于点E，作射线ED交CB的延长线于F点，连接PF．‎ ‎（1）求证：OD=OE；‎ ‎（2）求证：PF是⊙O的切线；‎ ‎（3）若∠POC=120°，AC=12，将扇形POA围成一个圆锥的侧面，求该圆锥的高．‎ ‎25、如图，在Rt△ABC中，∠A=90°，AB=6，AC=8，D，E分别是AC，BC的中点，点P从点A出发沿折线段AD﹣DE﹣EB以每秒3个单位长的速度向B匀速运动；点Q也从点A出发沿射线AB以每秒2个单位长的速度运动，当P与B重合时停止运动，点Q也随之停止运动．设点P，Q运动时间是t秒（t＞0）．‎ ‎（1）当点P到达终点B时，求t的值；‎ ‎（2）设△BPQ的面积为S，求出Q在线段AB上运动时，S与t的函数关系式；‎ ‎（3）是否存在t值，使PQ∥DB？若存在，求出t值，不存在说明理由．‎