2008浙江衢州市中考数学考试以及答案 9页

浙江省衢州市2008年初中毕业生学业水平考试 数 学 一、选择题(本大题有10小题，每小题4分，共40分。请选出各题中一个符合题意的正确选项填在相应的答案栏内，不选、多选、错选均不给分)‎ ‎1、的绝对值是( )‎ A、 B、‎2 C、 D、‎ ‎2、已知两圆的半径分别为3和4，圆心距为8，那么这两个圆的位置关系是( )‎ A、内切 B、相交 C、外切 D、外离 ‎3、下面形状的四张纸板，按图中线经过折叠可以围成一下直三棱柱的是( )‎ D、‎ C、‎ B、‎ A、‎ C A B O ‎4、某商品原价289元，经连续两次降价后售价为256元，设平均每降价的百分率为x，则下面所列方程正确的是( )‎ A、 B、 ‎ C、 D、‎ ‎5、把抛物线向右平移2个单位得到的抛物线是( )‎ A、 B、 C、 D、‎ ‎6、如图，C是以AB为直径的⊙O上一点，已知AB=5，BC=3，则圆心O到弦BC的距离是( )‎ A、1.5 B、‎2 C、2.5 D、3‎ ‎7、为参加电脑汉字输入比赛，甲和乙两位同学进行了6次测试，成绩如下表：‎ 甲和乙两位同学6次测试成绩(每分钟输入汉字个数)及部分统计数据表 第1次 第2次 第3次 第4次 第5次 第6次 平均数 方差 甲 ‎134‎ ‎137‎ ‎136‎ ‎136‎ ‎137‎ ‎136‎ ‎136‎ ‎1.0‎ 乙 ‎135‎ ‎136‎ ‎136‎ ‎137‎ ‎136‎ ‎136‎ ‎136‎ 有四位同学在进一步算得乙测试成绩的方差后分别作出了以下判断，其中说法正确的是( )‎ A、甲的方差大于乙的方差，所以甲的成绩比较稳定；‎ B、甲的方差小于乙的方差，所以甲的成绩比较稳定；‎ C、乙的方差小于甲的方差，所以乙的成绩比较稳定；‎ D、乙的方差大于甲的方差，所以乙的成绩比较稳定；‎ ‎8、某校准备组织师生观看北京奥运会球类比赛，在不同时间段里有3场比赛，其中2场是乒乓球比赛，1场是羽毛球比赛，从中任意选看2场，则选看的2场恰好都是乒乓球比赛的概率是( )‎ A、 B、 C、 D、‎ ‎13‎ ‎15‎ ‎17‎ ‎19‎ ‎9‎ ‎11‎ ‎3‎ ‎5‎ ‎7‎ ‎9、，和分别可以按如图所示方式“分裂”成2个、3个和4个连续奇数的和，也能按此规律进行“分裂”，则“分裂”出的奇数中最大的是( )‎ A、41 B、39 ‎ C、31 D、29‎ ‎10、如图，点O在Rt△ABC的斜边AB上，‎ ‎⊙O切AC边于点E，切BC边于点D，‎ A B D C E O 连结OE，如果由线段CD、CE及劣弧ED 围成的图形(阴影部分)面积与△AOE的面积相等，‎ 那么的值约为(取3.14) ( )‎ A、2.7 B、‎2.5 C、2.3 D、2.1‎ 二、填空题(本大题有6小题，每小题5分，共30分，将答案填在题中横线上)‎ A B D C ‎11、分解因式：‎ ‎12、如图，点C在线段AB的延长线上，，‎ ‎，则的度数是_____________‎ A B C E D ‎13、在半径为5的圆中，的圆心角所对的弧长为_________(结果保留)‎ ‎14、如图，点D、E分别在△ABC的边上AB、AC上，且 ‎，若DE=3，BC=6，AB=8，则AE的长 为___________‎ ‎15、汶川大地震牵动每个人的心，一方有难，八方支援，‎ ‎5位衢州籍在外打工人员也捐款献爱心。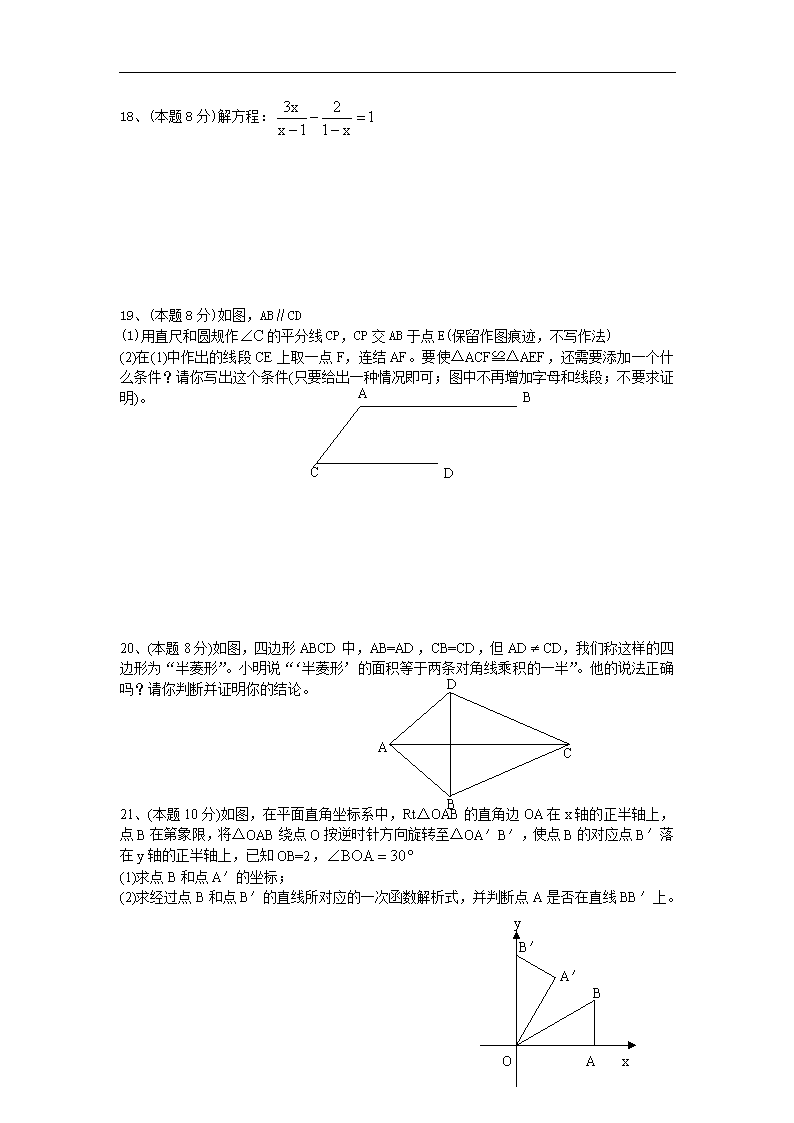已知5人平均 捐款560元(每人捐款数额均为百元的整数倍)，捐款数额最少的也捐了200元，最多的(只有1人)捐了800元，其中一人捐600元，600元恰好是5人捐款数额的中位数，那么其余两人的捐款数额分别是___________；‎ ‎16、已知n是正整数，(，)是反比例函数图象上的一列点，其中，，…，，记，，…，；若，则的值是_________；‎ 三、解答题(本大题有8小题，共80分，请务必写出解答过程)‎ ‎17、(本题8分)计算：‎ ‎18、(本题8分)解方程：‎ ‎19、(本题8分)如图，AB∥CD ‎(1)用直尺和圆规作的平分线CP，CP交AB于点E(保留作图痕迹，不写作法)‎ A B C D A C D B ‎(2)在(1)中作出的线段CE上取一点F，连结AF。要使△ACF≌△AEF，还需要添加一个什么条件？请你写出这个条件(只要给出一种情况即可；图中不再增加字母和线段；不要求证明)。‎ ‎20、(本题8分)如图，四边形ABCD中，AB=AD，CB=CD，但ADCD，我们称这样的四边形为“半菱形”。小明说“‘半菱形’的面积等于两条对角线乘积的一半”。他的说法正确吗？请你判断并证明你的结论。‎ ‎21、(本题10分)如图，在平面直角坐标系中，Rt△OAB的直角边OA在x轴的正半轴上，点B在第象限，将△OAB绕点O按逆时针方向旋转至△OA′B′，使点B的对应点B′落在y轴的正半轴上，已知OB=2，‎ ‎(1)求点B和点A′的坐标；‎ A O B A′‎ B′‎ x y ‎(2)求经过点B和点B′的直线所对应的一次函数解析式，并判断点A是否在直线BB′上。‎ ‎22、(本题12分)衢州市总面积8837平方千米，总人口247万人(截目2006年底)，辖区有6个县(市、区)，各县(市、区)的行政区域面积及平均每万人拥有面积统计如图1、图2所示 ‎(1)行政区域面积最大的是哪个县(市、区)？这个县(市、区)约有多少面积(精确到1平方千米)？‎ ‎(2)衢州市的人均拥有面积是多少(精确到1平方米)？6个县(市、区)中有几个县(市、区)的人均拥有面积超过衢州市人均拥有面积？‎ ‎(3)江山市约有多少人(精确到1万人)？‎ 衢州市各县(市、区)平均每万人拥有面积统计图 面积(平方千米)‎ ‎0‎ ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎60‎ ‎70‎ 衢江区 江山市 常山县 开化县 柯城区 龙游县 ‎14.85‎ ‎43.7‎ ‎34.79‎ ‎33.3‎ ‎63.54‎ ‎28.48‎ 县(市、区)‎ ‎23、(本题12分)1月底，某公司还有11000千克椪柑库存，这些椪柑的销售期最多还有60天，60天后库存的椪柑不能再销售，需要当垃圾处理，处理费为0.05元/吨。经测算，椪柑的销售价格定为2元/千克时，平均每天可售出100千克，销售价格降低，销售量可增加，每降低0.1元/千克，每天可多售出50千克。‎ ‎(1)如果按2元/千克的价格销售，能否在60天内售完这些椪柑？按此价格销售，获得的总毛利润是多少元()?‎ ‎(2)设椪柑销售价格定为x元/千克时，平均每天能售出y千克，求y关于x的函数解析式；如果要在2月份售完这些椪柑(2月份按28天计算)，那么销售价格最高可定为多少元/千克(精确到0.1元/千克)？‎ ‎24、(本题14分)已知直角梯形纸片OABC在平面直角坐标系中的位置如图所示，四个顶点的坐标分别为O(0，0)，A(10，0)，B(8，)，C(0，)，点T在线段OA上(不与线段端点重合)，将纸片折叠，使点A落在射线AB上(记为点A′)，折痕经过点T，折痕TP与射线AB交于点P，设点T的横坐标为t，折叠后纸片重叠部分(图中的阴影部分)的面积为S；‎ ‎(1)求∠OAB的度数，并求当点A′在线段AB上时，S关于t的函数关系式；‎ ‎(2)当纸片重叠部分的图形是四边形时，求t的取值范围；‎ ‎(3)S存在最大值吗？若存在，求出这个最大值，并求此时t的值；若不存在，请说明理由。‎ y x O B C A T y x O B C A T 浙江省2008年初中毕业生学业水平考试(衢州卷)数学试卷参考答案 一、选择题(本大题有10小题，每小题4分，共40分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 B D C A D B C B A C 二、填空题(本大题有6小题，每小题5分，共30分)‎ ‎11、 12、 13、 14、4 15、500元、700元或600元、600元 ‎16、51．2‎ 三、解答题(本大题有8小题，共80分)‎ ‎17、(本题8分)‎ 解：原式=‎ ‎ =‎ ‎18、(本题8分)‎ 解：方程两边都乘以，得：‎ C A B D E P F ‎ 解得：‎ ‎ 经检验：是原方程的根；‎ ‎19、(本题8分)‎ 解：(1)作图略；‎ ‎(2)取点F和画AF正确(如图)；‎ ‎ 添加的条件可以是：F是CE的中点；‎ ‎ AF⊥CE；∠CAF=∠EAF等。(选一个即可)‎ ‎20、(本题8分)‎ 解：正确。‎ 证明如下：‎ A B C D O 方法一：设AC，BD交于O，∵AB=AD，BC=DC，AC=AC，‎ ‎∴△ABC≌△ADE，‎ ‎∴∠BAC=∠DAC AB=AD，∴AO⊥BD ‎，‎ ‎ ‎ 方法二：∵AB=AD，‎ ‎∴点A在线段BD的中垂线上。‎ 又∵CB=CD，∴点C与在线段BD的中垂线上，‎ ‎∴AC所在的直线是线段BD的中垂线，即BD⊥AC；‎ 设AC，BD交于O，∵，‎ ‎21、(本题10分)‎ 解：(1)在△OAB中，‎ x A B A´‎ B´‎ y ‎∵，，∴AB=OB·‎ OA= OB·‎ ‎∴点B的坐标为(，1)‎ 过点A´作A´D垂直于y轴，垂足为D。‎ 在Rt△OD A´中 O DA´=OA´·，‎ OD=OA´·‎ ‎∴A´点的坐标为(，)‎ ‎(2)点B的坐标为(，1)，点B´的坐标为(0，2)，设所求的解析式为,则 解得，，∴‎ 当时，‎ ‎∴A´(，)在直线BB´上。‎ ‎22、(本题12分)‎ 解：(1)行政区域面积最大的是开化县，‎ ‎ 面积约为8837‎ ‎ (2)衢州市的人均拥有面积是 ‎ ‎ ‎ 衢江区和开化县2个县(市、区)的人均拥有面积超过衢州市人均拥有面积。‎ ‎ (3)，即江山市约有58万人。‎ ‎23、(本题12分)‎ 解：(1)，所以不能在60天内售完这些椪柑，‎ ‎ (千克)‎ ‎ 即60天后还有库存5000千克，总毛利润为 ‎ W=；‎ ‎ (2)‎ ‎ 要在2月份售完这些椪柑，售价x必须满足不等式 ‎ ‎ ‎ 解得 ‎ 所以要在2月份售完这些椪柑，销售价最高可定为1.4元/千克。‎ ‎24、(本题14分)‎ 解：(1) ∵A，B两点的坐标分别是A(10，0)和B(8，)，‎ ‎ ∴，‎ ‎ ∴‎ ‎ 当点A´在线段AB上时，∵，TA=TA´，‎ ‎ ∴△A´TA是等边三角形，且，‎ ‎ ∴，，‎ A A´‎ B P T E C O y x ‎ ∴，‎ ‎ 当A´与B重合时，AT=AB=，‎ ‎ 所以此时。‎ ‎ (2)当点A´在线段AB的延长线，且点P在线段AB(不与B重合)上时，‎ ‎ 纸片重叠部分的图形是四边形(如图(1)，其中E是TA´与CB的交点)，‎ A´‎ A T C O y x P F ‎ 当点P与B重合时，AT=2AB=8，点T的坐标是(2，0)‎ ‎ 又由(1)中求得当A´与B重合时，T的坐标是(6，0)‎ B E ‎ 所以当纸片重叠部分的图形是四边形时，。‎ ‎ (3)S存在最大值 ‎ 当时，，‎ ‎ 在对称轴t=10的左边，S的值随着t的增大而减小，‎ ‎∴当t=6时，S的值最大是。‎ 当时，由图，重叠部分的面积 ‎∵△A´EB的高是，‎ ‎∴‎ ‎ ‎ 当t=2时，S的值最大是；‎ 当，即当点A´和点P都在线段AB的延长线是(如图，其中E是TA´与CB的交点，F是TP与CB的交点)，‎ ‎∵，四边形ETAB是等腰形，∴EF=ET=AB=4，‎ ‎∴‎ 综上所述，S的最大值是，此时t的值是。‎