上海市中考数学试卷分析 12页

‎2013年上海市中考数学试卷分析 一、 试卷基本结构：‎ ‎2013年上海市中考数学试卷分值分布：‎ 科目 数学 题号 一、 选择题：1-6（共24分）；二、填空题：7-18（共48分）；‎ ‎ 三、解答题：19-25（共78分）‎ 题量 ‎25题 总分 ‎150分 ‎ 试卷结构从08年之后都没有变化，1-6题为选择题，占24分（每题4分）；7-18题为填空题，占48分（每题4分）；19-25题为解答题，占78分（其中，19-22每题10分，23-24每题12分，25题14分）。‎ 二、 模块分析:‎ ‎ 模块 题号 分值 ‎ 总分 命题特点 ‎ 代数 与 ‎ 方程 ‎1‎ ‎4‎ ‎40‎ 该模块共占40分，对比去年48分略有减少，其中代数部分3题12分，方程部分4题28分。‎ 该模块中几个常考考点：分式的乘除法、二次根式的定义及其计算、二元一次方程根的判别及其解法。不等式组和方程组的解法等在今年的中考卷中都有出现。‎ 本模块所占分值高，难度简单。‎ ‎2‎ ‎4‎ ‎7‎ ‎4‎ ‎8‎ ‎4‎ ‎9‎ ‎4‎ ‎19‎ ‎10‎ ‎20‎ ‎10‎ ‎ 图形 ‎ 与 ‎ 几何 ‎5‎ ‎4‎ ‎50‎ 该模块共占50分，对比去年46分有所提高。‎ 图形的对称及翻折问题、相似的判定和性质、向量、圆等考点为中考中填空选择的常考题型。‎ 从2012年以来，17题改为考“信息”类题型，今年继续沿用，主要考察学生对于新知识，题干条件的捕捉能力，难度简单。18题从09年以来一直考查翻折旋转等问题，综合度较高，属于难题。‎ 解直角三角形、四边形相关的证明题、相似相关考点为近几年必考题型。‎ ‎6‎ ‎4‎ ‎10‎ ‎4‎ ‎14‎ ‎4‎ ‎15‎ ‎4‎ ‎17‎ ‎4‎ ‎18‎ ‎4‎ ‎22‎ ‎10‎ ‎23‎ ‎12‎ ‎ 函数 ‎ 与 ‎ 分析 ‎3‎ ‎4‎ ‎ ‎ ‎ ‎ ‎22‎ 在近6年的中考中，10年仅考查2题共8分外， 12年考查3题18分，其余3年均考查4题16分，而今年考查高达4题22分，比去年还有所上升。‎ 由此可见这一模块的考查力度会继续加强，需要 引起重视。‎ ‎11‎ ‎4‎ ‎16‎ ‎4‎ ‎21‎ ‎10‎ 数据整理 与 概率统计 ‎4‎ ‎4‎ ‎ ‎ ‎ 12‎ 本模块自去年开始以1道选择题和2道填空题形式出现，改变以往以解答题形式考查。在未来几年会保持这种形式，占分12分，属简单题型。‎ ‎12‎ ‎4‎ ‎14‎ ‎4‎ ‎ 综合 ‎ 24‎ ‎ 12‎ ‎ 26‎ 综合性题目，难度与往年持平，分类讨论题目放到24题考查。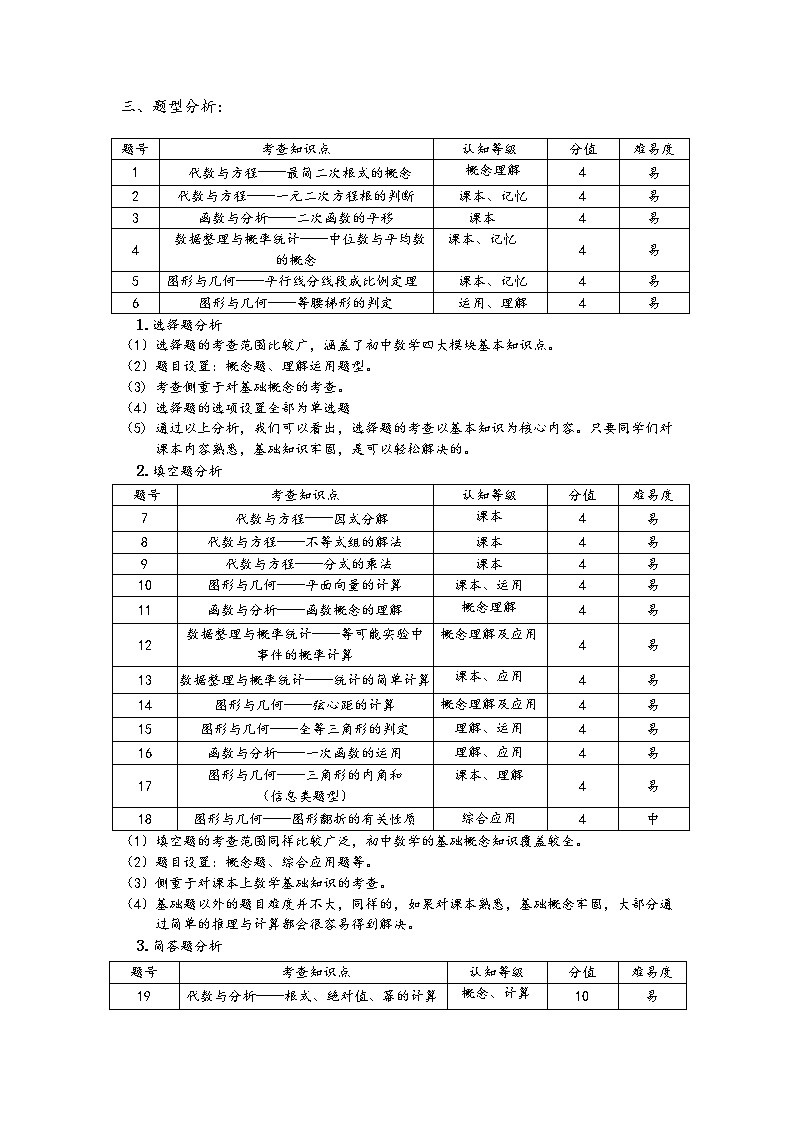‎ ‎ 25‎ ‎ 14‎ 三、题型分析：‎ 题号 考查知识点 认知等级 分值 难易度 ‎1‎ ‎ 代数与方程——最简二次根式的概念 ‎ 概念理解 ‎4‎ 易 ‎2‎ 代数与方程——一元二次方程根的判断 ‎ 课本、记忆 ‎4‎ 易 ‎3‎ 函数与分析——二次函数的平移 ‎ 课本 ‎4‎ 易 ‎4‎ ‎ 数据整理与概率统计——中位数与平均数的概念 ‎ 课本、记忆 ‎4‎ 易 ‎5‎ 图形与几何——平行线分线段成比例定理 ‎ 课本、记忆 ‎4‎ 易 ‎6‎ 图形与几何——等腰梯形的判定 ‎ 运用、理解 ‎4‎ 易 ‎ 1.选择题分析 ‎（1）选择题的考查范围比较广，涵盖了初中数学四大模块基本知识点。‎ ‎（2）题目设置：概念题、理解运用题型。‎ ‎（3) 考查侧重于对基础概念的考查。‎ ‎（4）选择题的选项设置全部为单选题 ‎（5) 通过以上分析，我们可以看出，选择题的考查以基本知识为核心内容。只要同学们对 ‎ ‎ 课本内容熟悉，基础知识牢固，是可以轻松解决的。‎ ‎ 2.填空题分析 ‎ 题号 考查知识点 认知等级 分值 难易度 ‎7‎ 代数与方程——因式分解 ‎ 课本 ‎4‎ 易 ‎8‎ 代数与方程——不等式组的解法 ‎ 课本 ‎4‎ 易 ‎9‎ ‎ 代数与方程——分式的乘法 ‎ 课本 ‎4‎ 易 ‎10‎ 图形与几何——平面向量的计算 ‎ 课本、运用 ‎4‎ 易 ‎11‎ 函数与分析——函数概念的理解 ‎ 概念理解 ‎4‎ 易 ‎12‎ 数据整理与概率统计——等可能实验中 事件的概率计算 概念理解及应用 ‎4‎ 易 ‎13‎ 数据整理与概率统计——统计的简单计算 ‎ 课本、应用 ‎4‎ 易 ‎14‎ 图形与几何——弦心距的计算 概念理解及应用 ‎4‎ ‎ 易 ‎15‎ 图形与几何——全等三角形的判定 ‎ 理解、运用 ‎4‎ 易 ‎16‎ 函数与分析——一次函数的运用 ‎ 理解、应用 ‎4‎ 易 ‎17‎ 图形与几何——三角形的内角和 ‎（信息类题型）‎ ‎ 课本、理解 ‎4‎ 易 ‎18‎ 图形与几何——图形翻折的有关性质 ‎ 综合应用 ‎4‎ 中 ‎（1）填空题的考查范围同样比较广泛，初中数学的基础概念知识覆盖较全。‎ ‎（2）题目设置：概念题、综合应用题等。 ‎ ‎（3）侧重于对课本上数学基础知识的考查。‎ ‎（4）基础题以外的题目难度并不大，同样的，如果对课本熟悉，基础概念牢固，大部分通 ‎ ‎ 过简单的推理与计算都会很容易得到解决。‎ ‎ 3.简答题分析 ‎ 题号 ‎ 考查知识点 认知等级 分值 难易度 ‎19‎ 代数与分析——根式、绝对值、幂的计算 ‎ 概念、计算 ‎10‎ 易 ‎20‎ 代数与分析——方程组的解法 ‎ 计算 ‎10‎ 易 ‎21‎ 函数与分析——一次函数与反比例函数的 相关性质 ‎ 理解、运用 ‎10‎ 易 ‎22‎ 图形与几何——解直角三角形的应用 ‎ 生活应用 ‎10‎ 易 ‎23‎ 图形与几何——平行四边形的性质、平行 线的相关性质、中位线等 ‎ 理解、‎ ‎ 综合运用 ‎12‎ 易 ‎24‎ 函数与几何的综合运用 ‎ 综合应用 ‎12‎ 中&难 ‎25‎ 函数与几何的综合运用 ‎ 综合应用 ‎14‎ 中&难 ‎（1）解答题重点考查了理解能力、重题干获取信息的能力和综合运用能力。‎ ‎（2）第19、20题考查学生代数的基本计算。‎ ‎（3）第21题考查学生对一次函数和反比例函数相关概念性质的理解及运用。‎ ‎（4）第22题涉及到数学知识与生活的联系，是今年出现的新题型，有助于学生更深刻理解 所学知识。‎ ‎（5）第23题综合考查了初中平面几何的大部分知识点，综合度较高，需要学生对几何知识 有较为深入的理解、掌握。‎ ‎（6）第24题和第25题是代数与几何相结合的题型，体现了“数形结合”的思想，综合程 度高，难度较大，是中考中区分度较大的题型。‎ 四、总结分析：‎ ‎ 1.题型分析：各部分知识点，所占分值及占总分值大致比率:‎ 模块 代数与方程 ‎ 图形与几何 ‎ ‎ 函数与分析 ‎ 数据整理与 概率统计 ‎ 综合 ‎ ‎ ‎ 题目 ‎1、2、7、‎ ‎8、9、19、‎ ‎20‎ ‎5、6、10、14、15、17、18、22、23‎ ‎ 3、11、‎ ‎16、21‎ ‎ 4、‎ ‎12、14‎ ‎24、25‎ ‎ ‎ ‎ 分值 ‎ ‎ ‎ 40分 ‎ ‎ ‎ 50分 ‎ ‎ ‎ 22分 ‎ ‎ ‎ 12分 ‎ ‎ ‎ 26分 ‎ ‎ ‎ 分值比例 ‎ ‎ ‎ 26.7%‎ ‎ ‎ ‎ 33.3%‎ ‎ ‎ ‎ 14.7%‎ ‎ 8%‎ ‎ 17.3%‎ ‎ 注重基础概念、基础知识考查，重视课本知识；有少部分试题与生活有密切的联系，考查应用方面的能力；另外注重几何知识的综合应用；综合题难度较大，着重考查“数形结合”思想，尤其是函数与几何相结合的综合性题型。‎ ‎ 2.试卷的特点：‎ ‎　 试题完全忠于书本，试题难度适中，以基础为主。试卷容量恰当，考查知识全面，覆盖面较大，几何所占比例较大，整张试卷基本再现了初中数学的知识网络。‎ ‎ 就整张数学试卷，试题主重体现了对课本的掌握和理解能力的培养。在信息的收集整理与处理、知识的记忆和整理、作图与识图、分析计算及科学探究方面提出了要求。‎ ‎2013年上海市初中毕业生统一学业考试 数学试卷 ‎ ‎（满分150分，考试时间100分钟）[来源:Z,xx,k.Com]‎ 考生注意：‎ ‎1．本试卷含三个大题，共25题；2．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效；3．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．‎ 一、选择题：（本大题共6题，每题4分，满分24分）‎ ‎【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上．】‎ ‎1．下列式子中，属于最简二次根式的是（ ）‎ ‎（A） ； （B） ； （C） ； （D）．‎ ‎2．下列关于x的一元二次方程有实数根的是（ ）‎ ‎（A）；（B）；（C） ；（D）．‎ ‎3．如果将抛物线向下平移1个单位，那么所得新抛物线的表达式是（ ）‎ ‎（A）；（B）； （C）；（D）．‎ 图1‎ ‎4．数据 0，1，1，3，3，4 的中位线和平均数分别是（ ）‎ ‎（A） 2和2.4 ； （B）2和2 ； （C）1和2； （D）3和2．‎ ‎5．如图1，已知在△ABC中，点D、E、F分别是边AB、AC、BC上的点，‎ DE∥BC，EF∥AB，且AD∶DB = 3∶5，那么CF∶CB等于（ ）‎ ‎（A） 5∶8 ； （B）3∶8 ； （C） 3∶5 ； （D）2∶5．‎ ‎6．在梯形ABCD中，AD∥BC，对角线AC和BD交于点O，下列条件中，‎ 能判断梯形ABCD是等腰梯形的是（ ）‎ ‎（A）∠BDC =∠BCD；（B）∠ABC =∠DAB；（C）∠ADB =∠DAC；（D）∠AOB =∠BOC．‎ 二、填空题：（本大题共12题，每题4分，满分48分）‎ ‎[请将结果直接填入答题纸的相应位置]‎ ‎7．因式分解： = _____________．‎ ‎8．不等式组 的解集是____________．‎ ‎9．计算：= ___________．‎ ‎10．计算：2 (─) + 3= ___________．‎ ‎11．已知函数 ，那么 = __________．‎ ‎12．将“定理”的英文单词theorem中的7个字母分别写在7张相同的卡片上，字面朝下随意放在桌子上，任取一张，那么取到字母e的概率为___________．‎ ‎13．某校报名参加甲、乙、丙、丁四个兴趣小组的学生人数如图2所示，那么报名参加甲组和丙组的人数之和占所有报名人数的百分比为___________．‎ 图2‎ 图3‎ 图4‎ ‎[来源:学§科§网Z§X§X§K]‎ ‎14．在⊙中，已知半径长为3，弦长为4，那么圆心到的距离为___________．‎ ‎15．如图3，在△和△中，点B、F、C、E在同一直线上，BF = CE，AC∥DF，请添加一个条件，使△≌△，这个添加的条件可以是____________．（只需写一个，不添加辅助线）‎ ‎16．李老师开车从甲地到相距240千米的乙地，如果邮箱剩余油量 （升）与行驶里程 （千米）之间是一次函数关系，其图像如图4所示，那么到达乙地时邮箱剩余油量是__________升．‎ 图5‎ ‎17．当三角形中一个内角α是另一个内角β的两倍时，我们称此三角形为“特征三角形”，其中α称为“特征角”．如果一个“特征三角形”的“特征角”为100°，那么这个“特征三角形”的最小内角的度数为__________．‎ ‎18．如图5，在△中，，， tan C = ，如果将△‎ 沿直线l翻折后，点落在边的中点处，直线l与边交于点，‎ 那么的长为__________．‎ 三、解答题：（本大题共7题，满分78分）‎ ‎（本大题共7题，19~22题10分，23、24题12分，25题14分，满分48分）‎ ‎[将下列各题的解答过程，做在答题纸的相应位置上]‎ ‎19．计算： ．‎ 图6‎ ‎20．解方程组： ．‎ ‎21．已知平面直角坐标系（如图6），直线 经 过第一、二、三象限，与y轴交于点，点（2，1）在这条直线上，‎ 联结，△的面积等于1．‎ ‎（1）求的值；‎ ‎（2）如果反比例函数（是常量，）[来源:学。科。网Z。X。X。K]‎ 的图像经过点，求这个反比例函数的解析式．‎ ‎22．某地下车库出口处“两段式栏杆”如图7-1所示，点是栏杆转动的支点，点是栏杆两段的连接点．当车辆经过时，栏杆升起后的位置如图7-2所示，其示意图如图7-3所示，其中⊥，‎ ‎∥，，米，求当车辆经过时，栏杆EF段距离地面的高度（即直线EF上任意一点到直线BC的距离）．‎ ‎（结果精确到‎0.1米，栏杆宽度忽略不计参考数据：sin 37° ≈ 0.60，cos 37° ≈ 0.80，tan 37° ≈ 0.75．）‎ 图7-1‎ 图7-2‎ 图7-3‎ A E F A E F A E F B C ‎23．如图8，在△中，， ，点为边的中点，交于点，‎ 图8‎ 交的延长线于点．‎ ‎（1）求证：；‎ ‎（2）联结，过点作的垂线交的 延长线于点，求证：．‎ ‎[来源:Zxxk.Com]‎ ‎24．如图9，在平面直角坐标系中，顶点为的抛物线经过点和轴正半轴上的点，= 2，．‎ ‎（1）求这条抛物线的表达式；‎ ‎（2）联结，求的大小；‎ ‎（3）如果点在轴上，且△与△相似，求点的坐标．‎ 图9‎ ‎25．在矩形中，点是边上的动点，联结，线段的垂直平分线交边于点，‎ 垂足为点，联结（如图10）．已知，，设．‎ ‎（1）求关于的函数解析式，并写出的取值范围；‎ ‎（2）当以长为半径的⊙P和以长为半径的⊙Q外切时，求的值；‎ ‎（3）点在边上，过点作直线的垂线，垂足为，如果，求的值．‎ 图10‎ ‎[来源:学,科,网]‎ 备用图beibeiyongtu