- 275.50 KB
- 2021-05-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
“一线三等角”构相似经典题型分类训练
(时间:90分钟 满分:100分)
班级 姓名 成绩 .
类型一 普通角
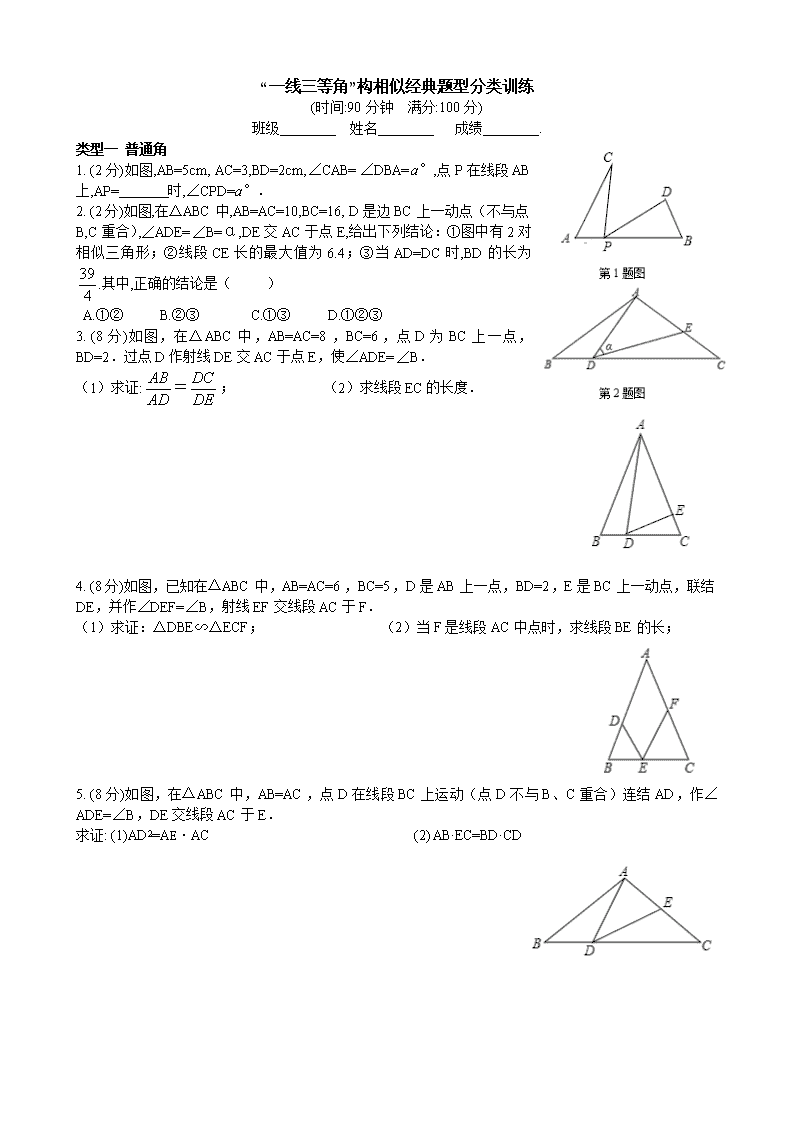
1. (2分)如图,AB=5cm, AC=3,BD=2cm,∠CAB=∠DBA=a°,点P在线段AB上,AP= 时,∠CPD=a°.
2. (2分)如图,在△ABC中,AB=AC=10,BC=16,D是边BC上一动点(不与点B,C重合),∠ADE=∠B=α,DE交AC于点E,给出下列结论:①图中有2对相似三角形;②线段CE长的最大值为6.4;③当AD=DC时,BD的长为.其中,正确的结论是( )
A.①② B.②③ C.①③ D.①②③
3. (8分)如图,在△ABC中,AB=AC=8,BC=6,点D为BC上一点,BD=2.过点D作射线DE交AC于点E,使∠ADE=∠B.
(1)求证:=; (2)求线段EC的长度.
4. (8分)如图,已知在△ABC中,AB=AC=6,BC=5,D是AB上一点,BD=2,E是BC上一动点,联结DE,并作∠DEF=∠B,射线EF交线段AC于F.
(1)求证:△DBE∽△ECF; (2)当F是线段AC中点时,求线段BE的长;
5. (8分)如图,在△ABC中,AB=AC,点D在线段BC上运动(点D不与B、C重合)连结AD,作∠ADE=∠B,DE交线段AC于E.
求证: (1)AD2=AE·AC (2) AB·EC=BD·CD
6. (8分) 如图①,在△ABC中,AC=BC,点D是线段AB上一动点,∠EDF绕点D旋转,在旋转过程中始终保持∠A=∠EDF,射线DE与边AC交于点M,射线DE与边BC交于点N,连接MN.
(1)找出图中的一对相似三角形,并证明你的结论;
(2)如图②,在上述条件下,当点D运动到AB的中点时,求证:在∠EDF绕点D旋转过程中,点D到线段MN的距离为定值.
类型二 45°或60°角
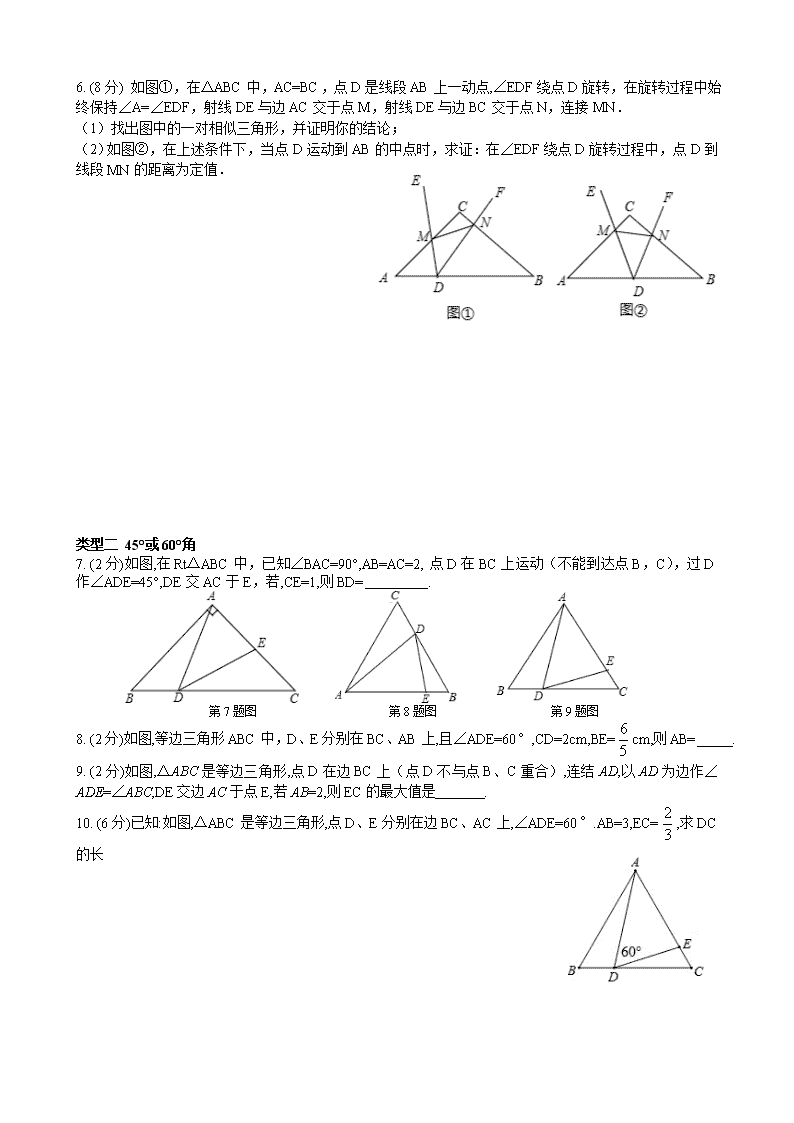
7. (2分)如图,在Rt△ABC中,已知∠BAC=90°,AB=AC=2,点D在BC上运动(不能到达点B,C),过D作∠ADE=45°,DE交AC于E,若,CE=1,则BD= .
第7题图 第8题图 第9题图
8. (2分)如图,等边三角形ABC中,D、E分别在BC、AB上,且∠ADE=60°,CD=2cm,BE=cm,则AB= .
9. (2分)如图,△ABC是等边三角形,点D在边BC上(点D不与点B、C重合),连结AD,以AD为边作∠ADE=∠ABC,DE交边AC于点E,若AB=2,则EC的最大值是 .
10. (6分)已知:如图,△ABC是等边三角形,点D、E分别在边BC、AC上,∠ADE=60°.AB=3,EC=,求DC的长
11. (6分)如图,在四边形ABCD中,AD∥BC,∠B=∠C=60°,AB=3,BC=7,P为BC边上的一点(不与B、C重合),过点P作∠APE=60°,PE交CD于点E.若CE=3,求PE的长.
类型三 90°角
12. (2分)矩形ABCD中,点E,F分别在AD、CD上,且BE⊥FE,则图中的三角形①,②,③,④一定相似的是( )
A.①和② B.①和③ C.②和④ D.①②和③
第12题图 第13题图 第14题图 第15题图 第16题图
13. (2分)如图,已知一次函数y=-x+1的图象与两坐标轴分别交于A、B,点C在x轴上,AC=4,第一象限内有一个点P,且PC⊥x轴于点C,若以点P、A、C为顶点的三角形与△OAB相似,则点P的坐标为( )
A.(4,8) B.(4,8)或(4,2) C.(6,8) D.(6,8)或(6,2)
14. (2分)如图,在正方形ABCD中,E是AD的中点,F是CD上一点,且CF=3FD.则图中相似三角形的对数是( )
A.1 B.2 C.3 D.4
15. (2分)如图,在梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,点P在线段AB上,当AP为多少时,△PAD与△PBC相似( )
A. B.1 C.6 D.或1或6
16. (2分)如图,点E在线段AB上,CA⊥AB于点A,DB⊥AB于点B,AC=1,AB=5,EB=2,点P是射线BD上的一个动点,则当BP= 时,△CEA与△EPB相似.
17. (6分)如图,在矩形ABCD中,E是BC上一点,AE⊥ED,若AE=4,CE=3BE.求这个四边形的面积.
18. (10分)如图,在四边形ABCD中,∠ABC=∠BCD=90°,点E为BC的中点,AE⊥DE.
(1)求证:△ABE∽△ECD;
(2)求证:AE2=AB•AD;
(3)若AB=1,CD=4,求线段AD,DE的长.
19. (10分)如图,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F,连接FC(AB>AE).
(1)求证:△AEF∽△DCE;
(2)△AEF与△EFC是否相似?若相似,证明你的结论;若不相似,请说明理由;
(3)设=k,若△AEF∽△BCF,则k= (请直接写出结果).
20. (10分)四边形ABCD中,点E在边AB上,连结DE,CE.
(1)若∠A=∠B=∠DEC=50°,找出图中的相似三角形,并说明理由;
(2)若四边形ABCD为矩形,AB=5,BC=2,且图中的三个三角形都相似,求AE的长.
(3)若∠A=∠B=90°,AD<BC,图中的三个三角形都相似,请判断AE和BE的数量关系并说明理由.
参考答案
1.2或3
2.D
3.(1)∵AB=AC,∴∠B=∠C,
∵∠ADC是△ABD的一个外角,
∴∠ACD=∠B+∠BAD=∠ADE+∠EDC,
又∵∠B=∠ADE,∴∠BAD=∠EDC,
∴△ABD∽△DCE,∴=;
(2)∵△ABD∽△DCE,∴=,
∵BC=6,BD=2,∴CD=4,∴=,解得EC=1.
4.(1)∵AB=AC=6,∴∠B=∠C,
∵∠BDE=180°-∠B-∠BED,∠CEF=180°-∠DEF-∠BED,
∵∠DEF=∠B,∴∠BDE=∠CEF,∴△DBE∽△ECF;
(2)∵△DBE∽△ECF,∴=,
∵F是线段AC中点,∴CF=AC=3
∴=,∴BE=2或3;
5.(1)∵AB=AC,∴∠B=∠C,
又∵∠ADE=∠B,∴∠ADE=∠C,
∵∠DAE=∠CAD,∴△ADE∽△ACD;
∴=,∴AD2=AE·AC.
(2)∵AB=AC,∴∠B=∠C,
∵∠ADC=∠BAD+∠B,∠ADC=∠ADE+∠EDC
∵∠ADE=∠B,∴∠BAD=∠EDC,
又∵∠B=∠C,∴△ABD∽△DCE.
∴=,∴AB·EC=BD·CD.
6.(1)△ADM∽△BND,理由如下:
∵AC=BC,∴∠A=∠B,
∵∠A+∠AMD=∠EDF+∠BDN,∠A=∠EDF,
∴∠AMD=∠BDN,∴△ADM∽△BND;
(2)证明:作DG⊥MN于G,DH⊥AM于H,如图②,
由(1)得,△ADM∽△BND,
∴△ADM∽△DNM,
∴∠AMD=∠NMD,又DG⊥MN,DH⊥AM,
∴DG=DH,即在∠EDF绕点D旋转过程中,点D到线段MN的距离为定值.
7.
8.5
9.
10.∵△ABC是等边三角形,∴∠B=∠C=60°,AB=AC,
∵∠B+∠BAD=∠ADE+∠CDE,∠B=∠ADE=60°,
∴∠BAD=∠CDE,∴△ABD∽△DCE,∴=.
设CD=x,则BD=3-x,∴=,∴x=1或x=2,∴DC=1或DC=2.
11.∵∠APE+∠EPC=∠BAP+∠B,∠APE=∠B,∴∠BAP=∠EPC
而∠C=∠B,∴△APB∽△PEC,∴=,
设BP=x,则PC=7-x,∴=,解得:x1=3,x2=4,
当BP=4时,△CEP为等边三角形,∴PE=CP=3,
当BP=3时,PE=,
∴PE的长度为3或.
12.B 13.D 14.C 15.D 16. 6或
17.易证:△ABE∽△DEA,则AE2=BE·AD.设BE=x,则EC=3x,AD=4x,解得x=2,可得AB=2,面积为16.
18.(1)证明:∵AE⊥DE,∴∠AED=90°,
∴∠AEB+∠CED=180°-90°=90°,
∵∠ABC=90°,∴∠BAE+∠AEB=90°,∴∠BAE=∠CED,
又∵∠ABC=∠BCD,∴△ABE∽△ECD;
19.(1)∵EF⊥EC,∴∠FEC=90°,即∠AEF+∠DEC=90°,
∵∠AEF+∠AFE=90°,∴∠DEC=∠AFE,
∵∠A=∠D=90°,∴△AEF∽△DCE;
(2)△AEF∽△ECF.证明如下:
延长FE与CD的延长线交于G,
∵E为AD的中点,AE=DE,∠AEF=∠GED,
∴Rt△AEF≌Rt△DEG.∴EF=EG.
∵CE=CE,∠FEC=∠CEG=90°,∴Rt△EFC≌Rt△EGC.
∴∠AFE=∠EGC=∠EFC.
又∵∠A=∠FEC=90°,∴Rt△AEF∽Rt△ECF;
(3) 点拨:要想使两三角形相似,已知的条件有一组直角,那么分两种情况进行讨论:当∠AFE=∠FCB时,那么∠AFE就和∠BFC互余,因此∠EFC就是直角,而∠FEC也是直角因此这种情况是不成立的.当∠AEF=∠FCB时,AE:BC=AF:BF,那么由于E是AD中点,因此BC=2AE,所以我们可得出BF=2AF,即AB=3AF,又根据(1)中AF=GD,AB=CD,我们可在△CEG中根据△EGD和△EDC相似,得出关于GD、ED、DC的比例关系,也就是AF、AB、AE的比例关系,有了AB=3AF,就能求出ED与AF的比例关系,也就求出了BC与AF的比例关系,以AF为中间值即可得出AB与BC的比例关系,也就求出了k的值.
20.(1)△DAE∽△EBC,
理由是:∵∠A=∠DEC=50°,
∴∠ADE+∠DEA=180°-∠A=130°,∠DEA+∠CEB=180°-∠DEC=130°,∴∠ADE=∠CEB,
∵∠A=∠B,∴△DAE∽△EBC;
(2)设AE=x,则BE=5-x,
∵∠ADE<90°,∠ECB<90°,∴∠DEC=90°,∴△DAE∽△EBC,
解得:x=1或4,即AE=1或4;
(3)AE=BE或BE=2AE,
理由是:①当∠A=∠B=∠DEC=90°时,∠DCE≠∠CEB,可得∠DCE=∠BCE,
所以△DEC∽△DAE∽△EBC,
②当∠DEC≠90°时,
∵△ADE∽△BCE,∠DEA=∠CEB,