上海市各区中考二模数学分类汇编压轴题专题含答案 23页

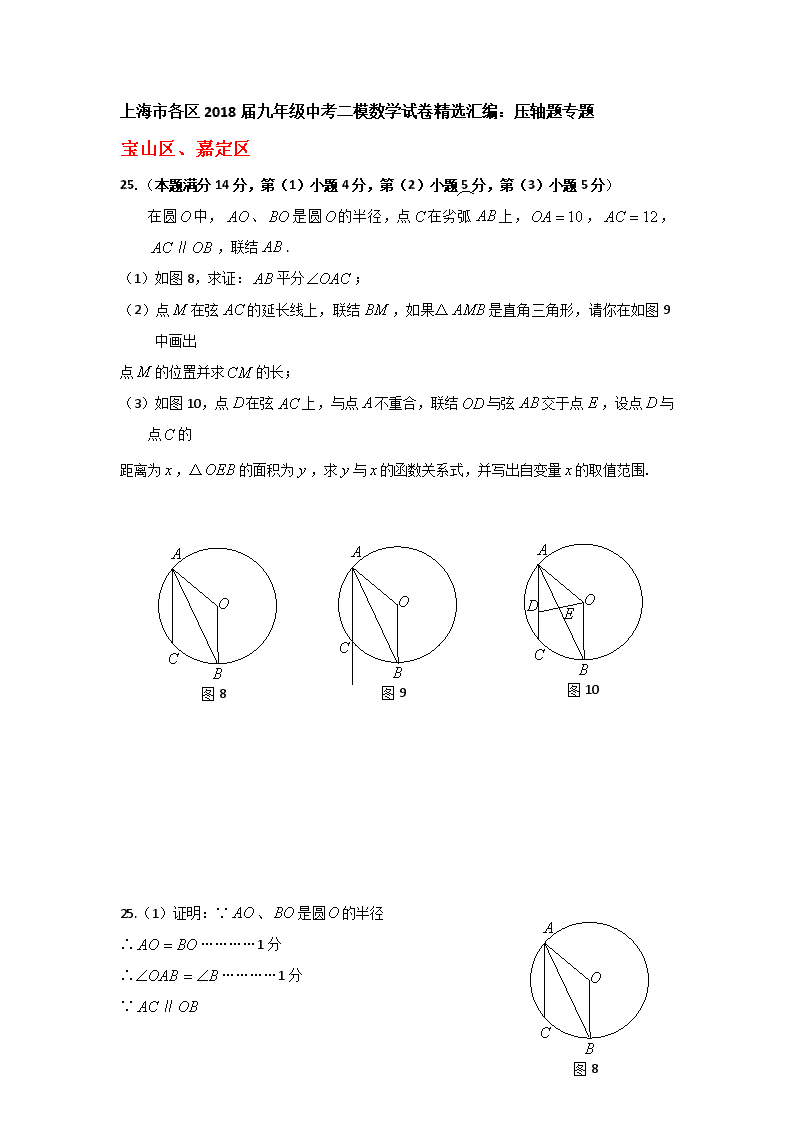
上海市各区 2018 届九年级中考二模数学试卷精选汇编：压轴题专题 宝山区、嘉定区 25.（本题满分 14 分，第（1）小题 4 分，第（2）小题 5 分，第（3）小题 5 分） 在圆 中， 、 是圆 的半径，点 在劣弧 上， ， ， ∥ ，联结 . （1）如图 8，求证： 平分 ； （2）点 在弦 的延长线上，联结 ，如果△ 是直角三角形，请你在如图 9 中画出 点 的位置并求 的长； （3）如图 10，点 在弦 上，与点 不重合，联结 与弦 交于点 ，设点 与 点 的 距离为 ，△ 的面积为 ，求 与 的函数关系式，并写出自变量 的取值范围. 25.（1）证明：∵ 、 是圆 的半径 ∴ …………1 分 ∴ …………1 分 ∵ ∥ O AO BO O C AB 10=OA 12=AC AC OB AB AB OAC∠ M AC BM AMB M CM D AC A OD AB E D C x OEB y y x x AO BO O BOAO = BOAB ∠=∠ AC OB A C B 图 8 O A C B 图 9 O A C B 图 10 OD E A C B 图 8 O ∴ …………1 分 ∴ ∴ 平分 …………1 分 (2)解：由题意可知 不是直角， 所以△ 是直角三角形只有以下两种情况: 和 ① 当 ，点 的位置如图 9-1……………1 分 过点 作 ,垂足为点 ∵ 经过圆心 ∴ ∵ ∴ 在 Rt△ 中， ∵ ∴ ∵ ∥ ∴ ∵ ∴ ∴四边形 是矩形 ∴ ∴ ……………2 分 ②当 ，点 的位置如图 9-2 由①可知 ， 在 Rt△ 中， ∴ ……………2 分 综上所述， 的长为 或 . 说明：只要画出一种情况点 的位置就给 1 分，两个点都画正确也给 1 分. （3）过点 作 ,垂足为点 由（1）、（2）可知， 由（2）可得： BBAC ∠=∠ BACOAB ∠=∠ AB OAC∠ BAM∠ AMB °=∠ 90AMB °=∠ 90ABM °=∠ 90AMB M O ACOH ⊥ H OH ACHCAH 2 1== 12=AC 6== HCAH AHO 222 OAHOAH =+ 10=OA 8=OH AC OB °=∠+∠ 180OBMAMB °=∠ 90AMB °=∠ 90OBM OBMH 10== HMOB 4=−= HCHMCM °=∠ 90ABM M 58=AB 55 2cos =∠CAB ABM 55 2cos ==∠ AM ABCAB 20=AM 8=−= ACAMCM CM 4 8 M O ABOG ⊥ G CABOAG ∠=∠ sinsin 5 5sin =∠CAB A C B 图 9-1 O M H A C B 图 9-2 O M A C B 图 10 OD E G ∵ ∴ ……………1 分 ∵ ∥ ∴ ……………1 分 又 , , ∴ ∴ ……………1 分 ∴ ∴ ……………1 分 自变量 的取值范围为 ……………1 分 长宁区 25．（本题满分 14 分，第（1）小题 4 分，第（2）小题 4 分，第（3）小题 6 分） 在圆 O 中，C 是弦 AB 上的一点，联结 OC 并延长，交劣弧 AB 于点 D，联结 AO、BO、 AD、BD. 已知圆 O 的半径长为 5 ，弦 AB 的长为 8． （1）如图 1，当点 D 是弧 AB 的中点时，求 CD 的长； （2）如图 2，设 AC=x， ，求 y 关于 x 的函数解析式并写出定义域； （3）若四边形 AOBD 是梯形，求 AD 的长． 10=OA 52=OG AC OB AD OB AE BE = BEAE −= 58 xAD −= 12 10=OB xBE BE −= − 12 10 58 xBE −= 22 580 5222 580 2 1 2 1 ×−×=××= xOGBEy xy −= 22 400 x 120 <≤ x yS S OBD ACO = ∆ ∆ O A C D B 图 1 O BA C D 图 2 BA O 备用图 第 25 题图 tututu 图 25.（本题满分 14 分，第（1）小题 4 分，第（2）小题 4 分，第（3）小题 6 分） 解：（1）∵OD 过圆心，点 D 是弧 AB 的中点，AB=8， ∴OD⊥AB， （2 分） 在 Rt△AOC 中， ，AO=5， ∴ （1 分） ， （1 分） （2）过点 O 作 OH⊥AB，垂足为点 H，则由（1）可得 AH=4，OH=3 ∵AC=x，∴ 在 Rt△HOC 中， ，AO=5， ∴ ， （1 分） ∴ （ ） （3 分） （3）①当 OB//AD 时， 过点 A 作 AE⊥OB 交 BO 延长线于点 E，过点 O 作 OF⊥AD,垂足为 点 F， 则 OF=AE， ∴ 在 Rt△AOF 中， ，AO=5， ∴ ∵OF 过圆心，OF⊥AD，∴ . （3 分） ②当 OA//BD 时， 过点 B 作 BM⊥OA 交 AO 延长线于点 M，过点 D 作 DG⊥AO，垂足为点 G， 则由①的方法可得 ， 在 Rt△GOD 中， ，DO=5， ∴ ， ， 42 1 == ABAC °=∠ 90ACO 322 =−= ACAOCO 5=OD 2=−=∴ OCODCD |4| −= xCH °=∠ 90CHO 258|4|3 22222 +−=−+=+= xxxHCHOCO 5 258 8 2 +−⋅−=⋅=⋅== ∆ ∆ ∆ ∆ ∆ ∆ xx x x OD OC BC AC S S S S S Sy OBD OBC OBC ACO OBD ACO x xxx 540 2582 − +−= 80 << x AEOBOHABS ABO ⋅=⋅=∆ 2 1 2 1  OFOB OHABAE ==⋅= 5 24 °=∠ 90AFO 5 722 =−= OFAOAF 5 142 == AFAD 5 24== BMDG °=∠ 90DGO 5 722 =−= DGDOGO 5 18 5 75 =−=−= GOAOAG 在 Rt△GAD 中， ，∴ （ 3 分） 综上得 崇明区 25．（本题满分 14 分，第(1)小题 4 分，第(2)小题 4 分，第(3)小题 6 分） 如 图 ， 已 知 中 ， ， ， ， D 是 AC 边 上 一 点 ， 且 ，联结 BD，点 E、F 分别是 BC、AC 上两点（点 E 不与 B、C 重合）， ，AE 与 BD 相交于点 G． （1）求证：BD 平分 ； （2）设 ， ，求 与 之间的函数关系式； （3）联结 FG，当 是等腰三角形时，求 BE 的长度． 25．（满分 14 分，第（1）小题 4 分，第（2）小题 4 分，第（3）小题 6 分） （1）∵ ， 又∵ ∴ ∴ ……………………………1 分 ∵ ∴ °=∠ 90DGA 622 =+= DGAGAD 65 14 或=AD ABC△ 8AB = 10BC = 12AC = 2AB AD AC= ⋅ AEF C∠ = ∠ ABC∠ BE x= CF y= y x GEF△ 8AB = 12AC = 2AB AD AC=  16 3AD = 16 2012 3 3CD = − = 2AB AD AC=  AD AB AB AC = （第 25 题图） A B C D G E F （备用图） A B C D 又∵ 是公共角 ∴ …………………………1 分 ∴ ， ∴ ∴ ∴ ………………………1 分 ∴ ∴ 平分 ………………………1 分 （2）过点 作 交 的延长线于点 ∵ ∴ ∵ ， ∴ ∴ ……1 分 ∵ ∴ ∴ ∴ …1 分 ∵ 即 ∵ ∴ 又∵ ∴ ……………………………………………………………1 分 ∴ ∴ ∴ …………………………………………………………1 分 （3）当△ 是等腰三角形时，存在以下三种情况： 1° 易证 ，即 ，得到 ………2 分 2° 易证 ，即 ， …………2 分 3° 易证 ，即 ………2 分 BAC∠ ADB ABC△ ∽△ ABD C=∠ ∠ BD AD BC AB = 20 3BD = BD CD= DBC C=∠ ∠ ABD DBC=∠ ∠ BD ABC∠ A AH BC∥ BD H AH BC∥ 16 43 20 5 3 AD DH AH DC BD BC = = = = 20 3BD CD= = 8AH = 16 3AD DH= = 12BH = AH BC∥ AH HG BE BG = 8 12 BG x BG −= 12 8 xBG x = + BEF C EFC= +∠ ∠ ∠ BEA AEF C EFC+ = +∠ ∠ ∠ ∠ AEF C=∠ ∠ BEA EFC=∠ ∠ DBC C=∠ ∠ BEG CFE△ ∽△ BE BG CF EC = 12 8 10 x x x y x += − 2 2 80 12 x xy − + += GEF GE GF= 2 3 GE BE EF CF = = 2 3 x y = 4BE = EG EF= BE CF= x y= 5 105BE = − + FG FE= 3 2 GE BE EF CF = = 3 2 x y = 3 89BE = − + 奉贤区 25．（本题满分 14 分，第(1)小题满分 5 分，第(2)小题满分 5 分，第(3)小题满分 4 分） 已知：如图 9，在半径为 2 的扇形 AOB 中，∠AOB=90°，点 C 在半径 OB 上，AC 的 垂直平分线交 OA 于点 D，交弧 AB 于点 E，联结 BE、CD． （1）若 C 是半径 OB 中点，求∠OCD 的正弦值； （2）若 E 是弧 AB 的中点，求证： ； （3）联结 CE，当△DCE 是以 CD 为腰的等腰三角形时，求 CD 的长． BCBOBE ⋅=2 图 9 A BC D O E 备用图 A BO 备用图 A BO 黄浦区 25．（本题满分 14 分） 如图，四边形 ABCD 中，∠BCD=∠D=90°，E 是边 AB 的中点.已知 AD=1，AB=2. （1）设 BC=x，CD=y，求 y 关于 x 的函数关系式，并写出定义域； （2）当∠B=70°时，求∠AEC 的度数； （3）当△ACE 为直角三角形时，求边 BC 的长. 25. 解：（1）过 A 作 AH⊥BC 于 H，————————————————————（1 分） 由∠D=∠BCD=90°，得四边形 ADCH 为矩形. 在△BAH 中，AB=2，∠BHA=90°，AH=y，HB= ， 所以 ，——————————————————————（1 分） 则 .———————————————（2 分） （2）取 CD 中点 T，联结 TE，————————————————————（1 分） 则 TE 是梯形中位线，得 ET∥AD，ET⊥CD. ∴∠AET=∠B=70°. ———————————————————————（1 分） 又 AD=AE=1， ∴∠AED=∠ADE=∠DET=35°. ——————————————————（1 分） 由 ET 垂直平分 CD，得∠CET=∠DET=35°，————————————（1 分） 所以∠AEC=70°＋35°=105°. ——————————————————（1 分） （3）当∠AEC=90°时， 易知△CBE≌△CAE≌△CAD，得∠BCE=30°， 则在△ABH 中，∠B=60°，∠AHB=90°，AB=2， 得 BH=1，于是 BC=2. ——————————————————————（2 分） 当∠CAE=90°时， 易知△CDA∽△BCA，又 ， 1x − 22 22 1y x= + − ( )2 2 3 0 3y x x x= − + + < < 2 2 2 4AC BC AB x= − = − 则 （ 舍 负 ） —————（ 2 分） 易知∠ACE<90°. 所以边 BC 的长为 2 或 .——————————————————（1 分） 金山区 25．（本题满分 14 分，第（1）小题 4 分，第（2）小题 5 分，第（3）小题 5 分） 如图 9，已知在梯形 ABCD 中，AD∥BC，AB=DC=AD=5， ，P 是线段 BC 上 一点，以 P 为圆心，PA 为半径的⊙P 与射线 AD 的另一个交点为 Q，射线 PQ 与射线 CD 相交于点 E，设 BP=x． （1）求证△ABP∽△ECP； （2）如果点 Q 在线段 AD 上（与点 A、D 不重合），设△APQ 的面积为 y， 求 y 关于 x 的函数关系式，并写出定义域； （3）如果△QED 与△QAP 相似，求 BP 的长． 2 2 1 4 1 17 24 AD CA x xAC CB xx − ±= ⇒ = ⇒ = − 1 17 2 + 3sin 5B = A B P C DQ E A B C D 图 9 备用图 25．解：（1）在⊙P 中，PA=PQ，∴∠PAQ ＝∠PQA，……………………………（1 分） ∵AD∥BC，∴∠PAQ ＝∠APB，∠PQA ＝∠QPC，∴∠APB ＝∠EPC，……（1 分） ∵梯形 ABCD 中，AD∥BC，AB=DC，∴∠B ＝∠C，…………………………（1 分） ∴△APB∽△ECP．…………………………………………………………（1 分） （2）作 AM⊥BC，PN⊥AD， ∵AD∥BC，∴AM∥PN，∴四边形 AMPN 是平行四边形， ∴AM=PN，AN=MP．………………………………………………………（1 分） 在 Rt△AMB 中，∠AMB=90°，AB=5，sinB= ， ∴AM=3，BM=4，∴PN=3，PM=AN=x-4，……………………………………（1 分） ∵PN⊥AQ，∴AN=NQ，∴AQ= 2x-8，……………………………………（1 分） ∴ ，即 ，………………………（1 分） 定义域是 ．………………………………………………………（1 分） （3）解法一：由△QED 与△QAP 相似，∠AQP＝∠EQD， ①如果∠PAQ＝∠DEQ，∵△APB∽△ECP，∴∠PAB＝∠DEQ， 又∵∠PAQ＝∠APB，∴∠PAB＝∠APB，∴BP=BA=5．………………………（2 分） ②如果∠PAQ＝∠EDQ，∵∠PAQ＝∠APB，∠EDQ＝∠C，∠B＝∠C， ∴∠B＝∠APB，∴ AB=AP，∵AM⊥BC，∴ BM=MP=4，∴ BP=8．………（2 分） 综上所述 BP 的长为 5 或者 8．………………………………………………（1 分） 解法二：由△QAP 与△QED 相似，∠AQP＝∠EQD， 在 Rt△APN 中， ， ∵QD∥PC，∴ ， ∵△APB∽△ECP，∴ ，∴ ， ①如果 ，∴ ，即 ， 解得 ………………………………………………………………………（2 分） 3 5 ( )1 1 2 8 32 2y AQ PN x= ⋅ ⋅ = ⋅ − ⋅ 3 12y x= − 134 2x< < ( )22 23 4 8 25AP PQ x x x= = + − = − + EQ EP QD PC = AP EP PB PC = AP EQ PB QD = AQ EQ QP QD = AQ AP QP PB = 2 2 2 8 8 25 8 25 x x x xx x − − += − + 5x = ②如果 ，∴ ，即 ， 解得 ………………………………………………………………………（2 分） 综上所述 BP 的长为 5 或者 8．…………………………………………………（1 分） 静安区 25．（本题满分 14 分，第（1）小题满分 4 分，第（2）小题满分 6 分，第（3）小题满分 4 分） 如图，平行四边形 ABCD 中，已知 AB=6，BC=9， ．对角线 AC、BD 交于 点 O．动点 P 在边 AB 上，⊙P 经过点 B,交线段 PA 于点 E．设 BP= x． （1） 求 AC 的长； （2） 设⊙O 的半径为 y，当⊙P 与⊙O 外切时， 求 y 关于 x 的函数解析式，并写出定义域； （3） 如果 AC 是⊙O 的直径，⊙O 经过点 E， 求⊙O 与⊙P 的圆心距 OP 的长． 25．（本题满分 14 分，第（1）小题 4 分，第（2）小题 6 分，第（3）小题 4 分） 解：（1）作 AH⊥BC 于 H，且 ，AB=6， 那么 …………（2 分） BC=9，HC=9-2=7， ， ……………………（1 分） ﹒ ………（1 分） （2）作 OI⊥AB 于 I，联结 PO, AC=BC=9，AO=4.5 ∴∠OAB=∠ABC, 3 1cos =∠ABC 23 16cos =×=∠⋅= ABCABBH 2426 22 =−=AH 9493222 =+=+= HCAHAC AQ DQ QP QE = AQ PB QP AP = 2 2 2 8 8 25 8 25 x x x x x x − = − + − + 8x = 3 1cos =∠ABC A 第 25 题图B P O C D E · 第 25 题备用图 A B O C D DA · 第 25 题图(1) B P O CH E · A 第 25 题图(2) B P O C D H E I ∴Rt△AIO 中， ∴AI=1.5，IO= ……………………（1 分） ∴PI=AB-BP-AI=6-x-1.5= ， ……………………（1 分） ∴Rt△PIO 中， ……（1 分） ∵⊙P 与⊙O 外切，∴ ……………………（1 分） ∴ = …………………………（1 分） ∵动点 P 在边 AB 上，⊙P 经过点 B,交线段 PA 于点 E．∴定义域：0 90o． 与∠ACD =∠CDB = 90o 矛盾． ∴四边形 ABDC 不可能为直角梯形．…………………………（2 分） 普陀区 25．（本题满分 14 分） 已知 是 的直径 延长线上的一个动点， 的另一边交 于点 C、D，两点 位于 AB 的上方， ＝6， ， ，如图 11 所示．另一个半径为 6 的 经 过点 C、D，圆心距 ． （1）当 时，求线段 的长； （2）设圆心 在直线 上方，试用 的代数式表示 ； （3）△ 在点 P 的运动过程中，是否能成为以 为腰的等腰三角形，如果能，试求 出此时 的值；如果不能，请说明理由． 8BC = 32cos 5CD BC BCD= ⋅ ∠ = 24sin 5BD BC BCD BE= ⋅ ∠ = = 32 165 10 25 CD AB = = 328 15 32 4 5 CE BE − = = CD CE AB BE ≠ AB CD AB P O⊙ BA P∠ O⊙ OP m＝ 1sin 3P＝ 1O⊙ 1OO n＝ 6m＝ 1O n m 1POO 1OO n D E BA C F OA B 备用图 P D OA B C 图 11 25．解： （1）过点 作 ⊥ ，垂足为点 ，联结 ． 在 Rt△ 中，∵ ， ，∴ ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（1 分） ∵ ＝6，∴ ． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（1 分） 由勾股定理得 ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（1 分） ∵ ⊥ ，∴ ． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（1 分） （2）在 Rt△ 中，∵ ， ，∴ ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（1 分） 在 Rt△ 中， ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（1 分） 在 Rt△ 中， ． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（1 分） 可得 ，解得 ． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（2 分） （3）△ 成为等腰三角形可分以下几种情况： ● 当圆心 、 在弦 异侧时 ① ，即 ，由 解得 ． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（1 分） 即圆心距等于 、 的半径的和，就有 、 外切不合题意舍去．（1 分） ② ，由 ， 解得 ，即 ，解得 ． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（1 分） ● 当圆心 、 在弦 同侧时,同理可得 ． ∵ 是钝角，∴只能是 ，即 ，解得 ．∙∙∙∙∙∙∙∙∙∙∙（2 分） O OH CD H OC POH 1sin 3P＝ 6PO = 2OH = AB 3OC＝ 5CH = OH DC 2 2 5CD CH= = POH 1sin 3P＝ PO m＝ 3 mOH＝ OCH 2 2 9 3 mCH  −   ＝ 1O CH 2 2 36 3 mCH n − −  ＝ 2 2 36 93 3 m mn   − − −      ＝ 23 81 2 nm n −＝ 1POO 1O O CD 1OP OO＝ m n＝ 23 81 2 nn n −＝ 9n＝ O⊙ 1O⊙ O⊙ 1O⊙ 1 1O P OO＝ 2 22 3 3 m mn m− + −( ) ( ) n＝ 2 3m n＝ 2 3 n 23 81 2 n n −＝ 9 155n＝ 1O O CD 281 3 2 nm n −＝ 1POO∠ m n= 281 3 2 nn n −＝ 9 55n＝ 综上所述， 的值为 或 ． 青浦区 25.（本题满分 14 分，第（1）小题 4 分，第（2）小题 6 分，第（3）小题 4 分） 如图 9-1，已知扇形 MON 的半径为 ，∠MON= ，点 B 在弧 MN 上移动，联结 BM，作 OD BM，垂足为点 D，C 为线段 OD 上一点，且 OC=BM，联结 BC 并延长交半径 OM 于点 A，设 OA= x，∠COM 的正切值为 y． （1）如图 9-2，当 AB OM 时，求证：AM =AC； （2）求 y 关于 x 的函数关系式，并写出定义域； （3）当△OAC 为等腰三角形时，求 x 的值. 25．解：（1）∵OD⊥BM，AB⊥OM，∴∠ODM =∠BAM =90°． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（1 分） ∵∠ABM +∠M =∠DOM +∠M，∴∠ABM =∠DOM．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（1 分） ∵∠OAC=∠BAM，OC =BM， ∴△OAC≌△ABM，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（1 分） ∴AC =AM． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（1 分） （2）过点 D 作 DE//AB，交 OM 于点 E． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（1 分） ∵OB＝OM，OD⊥BM，∴BD＝DM．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（1 分） ∵DE//AB， ∴ ，∴AE＝EM， ∵OM= ，∴AE＝ ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（1 分） ∵DE//AB， 2 90 ⊥ ⊥ n 9 55 9 155 =MD ME DM AE 2 ( )1 22 − x O M N DC B A 图 9-1 O M N DC B A 图 9-2 N MO 备用图 ∴ ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（1 分） ∴ ， ∴ ．（ ）∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（2 分） （3）（i） 当 OA=OC 时， ∵ ， 在 Rt△ODM 中， ．∵ ， ∴ ．解得 ，或 （舍）．（2 分） （ii）当 AO=AC 时，则∠AOC =∠ACO， ∵∠ACO >∠COB，∠COB =∠AOC，∴∠ACO >∠AOC， ∴此种情况不存在．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（1 分） （ⅲ）当 CO=CA 时， 则∠COA =∠CAO= ， ∵∠CAO >∠M，∠M= ，∴ > ，∴ > ， ∴ ，∵ ，∴此种情况不存在． ∙∙∙∙∙∙∙∙∙∙∙（1 分） 松江区 25．（本题满分 14 分，第（1）小题 4 分，第（2）小题每个小题各 5 分） 如图，已知 Rt△ABC 中，∠ACB=90°，BC=2，AC=3，以点 C 为圆心、CB 为半径的圆交 AB 于点 D，过点 A 作 AE∥CD，交 BC 延长线于点 E. （1）求 CE 的长； （2）P 是 CE 延长线上一点，直线 AP、CD 交于点 Q. ① 如果△ACQ ∽△CPQ，求 CP 的长； ② 如果以点 A 为圆心，AQ 为半径的圆与⊙C 相切，求 CP 的长. 2= =OA OC DM OE OD OD 2 =DM OA OD OE 2 = + xy x 0 2< ≤x 1 1 1 2 2 2 = = =DM BM OC x 2 2 212 4 = − = −OD OM DM x = DMy OD 2 1 2 1 22 4 = +− x x xx 14 2 2 −=x 14 2 2 − −=x α 90 α° − α 90 α° − α 45° 2 90α∠ = > °BOA 90∠ ≤ °BOA (第 25 题图) CB A D E (备用图) CB A D E 25．（本题满分 14 分，第（1）小题 4 分，第（2）小题每个小题各 5 分） 解：（1）∵AE∥CD ∴ …………………………………1 分 ∵BC=DC ∴BE=AE …………………………………1 分 设 CE=x 则 AE=BE=x+2 ∵ ∠ACB=90°， ∴ 即 ………………………1 分 ∴ 即 …………………………………1 分 （2）① ∵△ACQ ∽△CPQ，∠QAC>∠P ∴∠ACQ=∠P…………………………………1 分 又∵AE∥CD ∴∠ACQ=∠CAE ∴∠CAE=∠P………………………………1 分 ∴△ACE ∽△PCA，…………………………1 分 ∴ …………………………1 分 即 ∴ ……………………………1 分 BC DC BE AE = 2 2 2AC CE AE+ = 2 29 ( 2)x x+ = + 5 4x = 5 4CE = 2AC CE CP= ⋅ 2 53 4 CP= ⋅ 36 5CP = CB A D E P Q (第 25 题图) CB A D E ②设 CP=t，则 ∵∠ACB=90°， ∴ ∵AE∥CD ∴ ……………………………1 分 即 ∴ ……………………………1 分 若两圆外切，那么 此时方程无实数解……………………………1 分 若两圆内切切，那么 ∴ 解之得 ………………………1 分 又∵ ∴ ………………………1 分 徐汇区 25. 已知四边形 是边长为 10 的菱形，对角线 、 相交于点 ，过点 作 ∥ 交 延长线于点 ，联结 交 于点 . （1）如图 1，当 时，求 的长； （2）如图 2，以 为直径作⊙ ，⊙ 经过点 交边 于点 （点 、 不重合）， 设 的长为 ， 的长为 ； ① 求 关于 的函数关系式，并写出定义域； 5 4PE t= − 29AP t= + AQ EC AP EP = 2 5 54 5 4 59 4 AQ tt t = = −+ − 25 9 4 5 tAQ t += − 25 9 14 5 tAQ t += =− 25 9 54 5 tAQ t += =− 5 4t > 215 40 16 0t t− + = 20 4 10 15t ±= 20 4 10 15t += ABCD AC BD E C CF DB AB F EF BC H EF BC⊥ AE EF O O C CD G C G AE x EH y y x ③ 联结 ，当 是以 为腰的等腰三角形时，求 的长.EG DEG∆ DG AE 杨浦区 25、（本题满分 14 分，第（1）小题 4 分，第（2）小题 6 分，第（3）小题 4 分） 如图 9，在梯形 ABCD 中，AD//BC,AB=DC=5，AD=1，BC=9，点 P 为边 BC 上一动点，作 PH⊥ DC，垂足 H 在边 DC 上，以点 P 为圆心 PH 为半径画圆，交射线 PB 于点 E. （1） 当圆 P 过点 A 时，求圆 P 的半径； （2） 分别联结 EH 和 EA，当△ABE △CEH 时，以点 B 为圆心，r 为半径的圆 B 与圆 P 相 交，试求圆 B 的半径 r 的取值范围； （3） 将劣弧 沿直线 EH 翻折交 BC 于点 F，试通过计算说明线段 EH 和 EF 的比值为定值， 并求出此定值。