中考数学试题分类大全39 圆的有关性质 49页

一、选择题 ‎1．（2010安徽省中中考） 如图，⊙O过点B 、C。圆心O在等腰直角△ABC的内部，∠BAC＝900，OA＝1，BC＝6，则⊙O的半径为………………（ ）‎ A）B）C）D） ‎ ‎【答案】C ‎2．（2010安徽蚌埠二中）以半圆的一条弦（非直径）为对称轴将弧折叠后 与直径交于点，若，且，则的 长为 ‎ A． B． C． D．4‎ ‎【答案】A ‎3．（2010安徽芜湖）如图所示，在圆⊙O内有折线OABC，其中OA＝8，AB＝12，∠A＝∠B＝60°，则BC的长为（）‎ A．19 B．‎16 C．18 D．20‎ ‎【答案】D ‎4．（2010甘肃兰州） 有下列四个命题：①直径是弦；②经过三个点一定可以作圆；③三角形的外心到三角形各顶点的距离都相等；④半径相等的两个半圆是等弧．其中正确的有 ‎ A．4个 B．3个 C． 2个 D． 1个 ‎【答案】B ‎5．（2010甘肃兰州） 将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上．点A、B的读数分别为86°、30°，则∠ACB的大小为 A．15 B．‎28 ‎C．29 D．34‎ ‎【答案】B ‎6．（2010江苏南通） 如图，⊙O的直径AB=4，点C在⊙O上，∠ABC=30°，则AC的长是 A．1 B．‎ C． D．2‎ ‎【答案】D ‎7．（2010山东烟台）如图，△ ABC内接于⊙O，D为线段AB的中点，延长OD交⊙O于点E，连接AE，BE，则下列五个结论①AB⊥DE,②AE=BE,③OD=DE,④∠AEO=∠C,⑤,正确结论的个数是 A、2 B、‎3 C、4 D、5‎ ‎【答案】B ‎ ‎8．（2010台湾）如图(二)，为圆O的直径，C、D两点均在圆上，其中与交于 ‎ E点，且^。若=4，=2，则长度为何？‎ ‎ (A) 6 (B) 7 (C) 8 (D) 9 。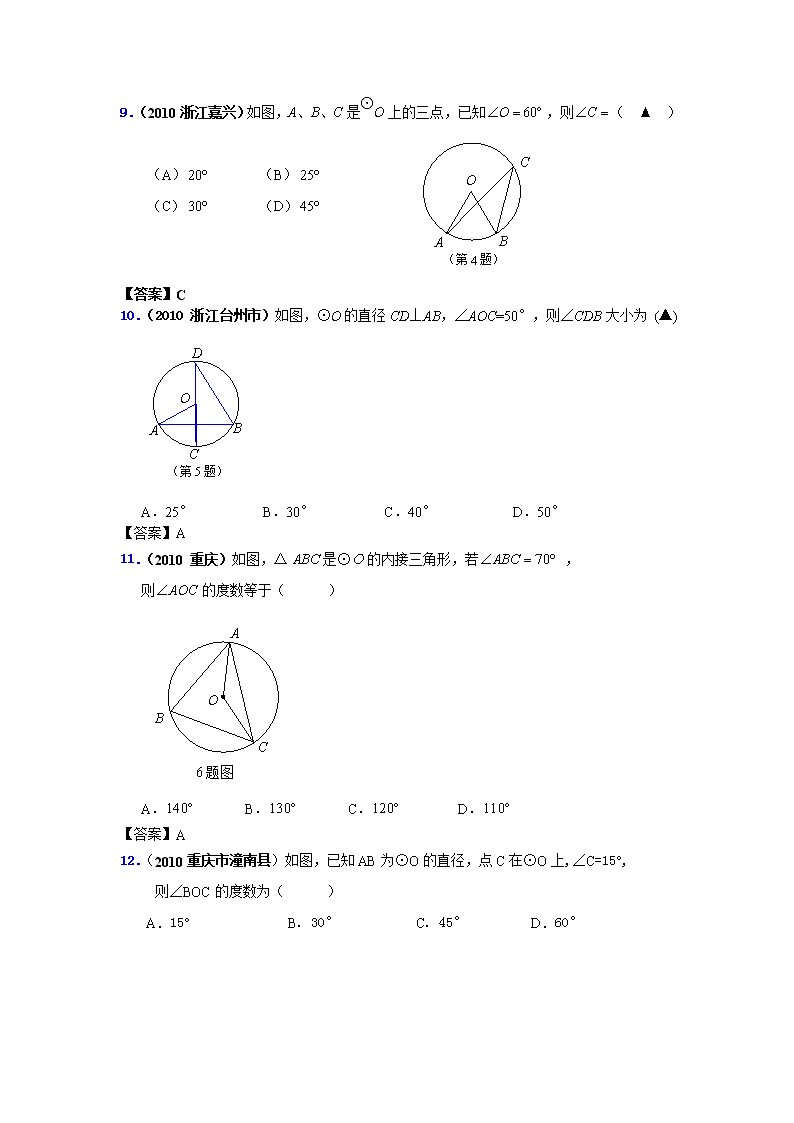‎ A B C D E O 图(二)‎ ‎【答案】C ‎9．（2010浙江嘉兴）如图，A、B、C是⊙O上的三点，已知，则（　▲　）‎ ‎（第4题）‎ ‎（A） （B）‎ ‎（C） （D）‎ ‎【答案】C ‎ ‎10．（2010 浙江台州市）如图，⊙O的直径CD⊥AB，∠AOC=50°，则∠CDB大小为 (▲)‎ ‎（第5题）‎ A B O C D A．25° B．30° C．40° D．50°‎ ‎【答案】A ‎11．（2010 重庆）如图，△是⊙的内接三角形，若 ，‎ 则的度数等于（ ） ‎ ‎6题图 A O C B A． B． C． D． ‎ ‎【答案】A ‎ ‎12．（2010重庆市潼南县）如图，已知AB为⊙O的直径，点C在⊙O上,∠C=15°,‎ 则∠BOC的度数为（ ）‎ ‎ A．15° B. 30° C. 45° D．60° ‎ ‎【答案】B ‎ ‎13．（2010 福建德化）如图，点B、C在⊙上，且BO=BC，则圆周角等于（ ）‎ ‎ A． B． C． D．‎ ‎【答案】D ‎ ‎14．（2010 福建晋江）如图， 、、是⊙上的三点，且是优弧上与点、点不同的一点，若是直角三角形，则必是( 　 ) .‎ A O B C 第6题图 A.等腰三角形 　　　　　 　　　 B.锐角三角形 ‎ C.有一个角是的三角形　　　　 D.有一个角是的三角形 ‎【答案】D ‎ ‎15．（2010浙江金华）如图，△ABC内接于⊙O，∠A=40°，则∠BOC的度数为（ ▲ ）‎ ‎ ‎ A C B O ‎ A. 20° B. 40° C. 60° D. 80° ‎ ‎【答案】D ‎ ‎16．（2010四川宜宾）若⊙O的半径为‎4cm，点A到圆心O的距离为‎3cm，那么点A与⊙O的位置关系是( )‎ A．点A在圆内 B．点A在圆上 c．点A在圆外 D．不能确定 ‎【答案】A ‎ ‎17．（2010浙江绍兴）已知⊙O的半径为5,弦AB的弦心距为3,则AB的长是( )‎ A.3 B‎.4 C.6 D.8‎ ‎【答案】D ‎ ‎18．（2010湖南衡阳）如图，将三角尺的直角顶点放在直尺的一边上，∠1=30°，∠2=50°，则的度数等于（ ）‎ A．50° B．30° C．20° D．15°‎ ‎1‎ ‎2‎ ‎3‎ ‎【答案】C ‎ ‎19．（2010湖南衡阳）如图，已知⊙O的两条弦AC，BD相交于点E，∠A=70o，∠c=50o， ‎ 那么sin∠AEB的值为( )‎ ‎ A. B. C. D. ‎ ‎【答案】D ‎ ‎20．（2010 河北）如图3，在5×5正方形网格中，一条圆弧经过A，B，C三点， ‎ 那么这条圆弧所在圆的圆心是 M R Q 图3‎ A B C P A．点P B．点Q C．点R D．点M ‎【答案】B ‎21．（2010 山东省德州）已知三角形的三边长分别为3,4,5，则它的边与半径为1的圆的公共点个数所有可能的情况是 ‎(A)0，1，2，3 (B)0，1，2，4 (C)0，1，2，3，4 (D)0，1，2，4，5 ‎ ‎【答案】C ‎ ‎22．（2010福建宁德）如图，在⊙O中，∠ACB＝34°，则∠AOB的度数是（ ）．‎ 第5题图 A O C B A.17° B.34° C.56° D.68°‎ ‎【答案】D ‎ ‎23．（2010年贵州毕节）如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为‎16cm2,则该半圆的半径为（　 　）‎ D C B A O A. cm B. ‎9 cm C. cm D. cm ‎【答案】C.‎ ‎24．（2010湖北武汉）如图，的直径AB长为10，弦AC长为6，∠ACB的平分线交⊙O于D，则CD的长为（ ）‎ A、7 B、 C、 D、9‎ ‎【答案】B ‎ ‎25．（2010浙江湖州）如图，已知⊙O的直径AB⊥弦CD于点E，下列结论中一定正确的是（ ）‎ A．AE＝OE B．CE＝DE C．OE＝CE D．∠AOC＝60°‎ ‎．‎ ‎【答案】B．‎ ‎26．（2010湖北荆门）如图，MN是半径为1的⊙O的直径，点A在⊙O上，‎ ‎∠AMN=30°，B为AN弧的中点，点P是直径MN上一个动点，则PA+PB的最小值为 A．2 B． C．1 D．2‎ ‎【答案】B ‎ 27．（2010山东潍坊）如图，AB是⊙O的弦，半径OC⊥AB于D点，且AB＝‎6cm，OD＝‎4cm，则DC的长为（ ）．‎ A．‎5cm B．2．‎5cm C．‎2cm D．‎‎1cm ‎【答案】D ‎ ‎28．（2010湖南郴州）如图，是的直径，为弦，于，‎ 则下列结论中不成立的是 第7题 Ａ．　　　　Ｂ．‎ Ｃ．　　　Ｄ．‎ ‎【答案】 D ‎ ‎29．（2010湖北荆州）△ABC中，∠A=30°，∠C=90°，作△ABC的外接圆．如图，若 弧A B 的长为‎12cm，那么弧AC 的长是 ‎ A．‎10cm B．‎9cm C．‎8cm D．‎‎6cm ‎【答案】C ‎ ‎30．（2010湖北鄂州）如图，已知AB是⊙O的直径，C是⊙O上的一点，连结AC，过点C作直线CD⊥AB交AB于点Ｄ，Ｅ是OＢ上的一点，直线CE与⊙O交于点F，连结AF交直线CD于点G，AC=,则AG·AF是 Ａ．10　　　Ｂ．12　　　Ｃ．16　　　Ｄ．8‎ ‎【答案】D ‎31（2010云南红河哈尼族彝族自治州）如图2，已知BD是⊙O的直径，⊙O的弦AC⊥BD于点E，若∠AOD=60°，则∠DBC的度数为 ‎ A.30° B.40°‎ C.50° D.60°‎ ‎【答案】A ‎32. （2010四川乐山）如图，一圆弧过方格的格点A、B、C，试在方格中建立平面直角坐标系，使点A的坐标为（－2，4），则该圆弧所在圆的圆心坐标是（ ）‎ A. （－1，2）B. （1，－1）C. （－1，1）D. （2，1）‎ A C B ‎【答案】C ‎ ‎33. （2010黑龙江哈尔滨）如图，AB是⊙O的弦，半径OA=2，，则弦AB的长是 （ ）‎ ‎ （A） （B） （C） （D）．‎ ‎【答案】B ‎ ‎34. （2010陕西西安）如图，点A、B、P在⊙O上，且∠APB=50°若点M是⊙O上的动 点，要使△ABM为等腰三角形，则所有符合条件的点M有 ‎ A．1个 B．2个 C．3个 D．4个 ‎【答案】D ‎ ‎35. （2010 福建三明）如图，在平面直角坐标系中，点P在第一象限，⊙P与x轴相切于点Q，与y轴交于M（0，2）， N（0，8）两点，则点P的坐标是 （ ）‎ ‎ A．（5，3） B．（3，5） ‎ ‎ C．（5，4） D．（4，5）‎ ‎【答案】D ‎ ‎36. （2010湖北襄樊）已知⊙O的半径为‎13cm，弦AB//CD，AB=‎24cm，CD=‎10cm，则AB、CD之间的距离为（ ）‎ A．‎17cm B．‎7 cm C．‎12 cm D．‎17 cm或‎7 cm 图(1) 图(2)‎ ‎【答案】D ‎ ‎37. （2010 四川绵阳）如图，等腰梯形ABCD内接于半圆D，且AB = 1，BC = 2，则OA =（ ）．‎ A． B． C． D．‎ C B A O D ‎【答案】A ‎ ‎38．（2010 贵州贵阳）如图1，AB是⊙O的直径，C是⊙O上的一点，若AC=8，‎ AB=10，OD⊥BC于点D，则BD的长为 ‎（A）1.5         （B）3          （C）5          （D）6 ‎ ‎(图1)‎ ‎【答案】B ‎ ‎39．（2010湖北十堰）下列命题中，正确命题的序号是（ ）‎ ‎①一组对边平行且相等的四边形是平行四边形 ‎②一组邻边相等的平行四边形是正方形 ‎③对角线相等的四边形是矩形 ‎④对角互补的四边形内接于圆 A．①② B．②③ C．③④ D．①④‎ ‎【答案】D ‎ ‎40．（2010 重庆江津）已知：点A、B、P为⊙O上的点，若∠PBO=15º,‎ 且PA∥OB，则∠AOB=（ ）‎ A． 15º B． 20º C． 30º D． 45º ‎ ‎【答案】C ‎ ‎41．（2010青海西宁）如图，在半径为5的⊙O中，若弦AB=8，则△AOB的面积为 A. 24 B. ‎16 C. 12 D.8 ‎ ‎【答案】C ‎ ‎42．如图，锐角△ABC的顶点A、B、C均在⊙O上，∠OAC=20°，则∠B的度数为 A．40° B．60° C．70° D．80°‎ ‎【答案】C ‎ ‎43．（2010新疆维吾尔自治区新疆建设兵团）如右图，王大爷家屋后有一块长‎12m，宽‎8m的矩形空地，他在以BC为直径的半圆内种菜，他家养的一只羊平时拴在A处，为了不让羊吃到菜，拴羊的绳子可以选用（ ）‎ A. ‎3m B‎.5m C‎.7m D. ‎‎9m ‎【答案】A ‎ ‎44．（2010新疆乌鲁木齐）如图2，在平面直角坐标系中，点A、B、C的坐标分别为 ‎（1，4），（5，4），（1，-2），则外接圆的圆心坐标是 ‎ A．（2，3） B．（3，2）‎ ‎ C．（1，3） D．（3，1）‎ ‎【答案】D ‎ ‎45．（2010广西梧州）如图6，AB是⊙O的直径，弦CD⊥AB于点E，则下列结论一定正确的个数有①CE=DE；②BE=OE；③=；④∠CAB=∠DAB；⑤AC=AD。（ ）‎ A．4个 B．3个 C．2个 D．1个 ‎ 图6‎ B C D E O A ‎·‎ ‎【答案】A ‎ ‎46．（2010广东佛山）如图，直线与两个同心圆分别交于图示的各点，则正确的是 A．MP与RN的大小关系不定 B.MP=RN C.MP＜RN D.MP＞RN ‎【答案】B ‎ ‎47．（2010天门、潜江、仙桃）如图，半圆O的直径AB=7，两弦AB、CD相交于点E，弦CD=，且BD=5，则DE等于( )‎ ‎ A. B. C. D.‎ ‎．‎ ‎【答案】C.‎ ‎48．（2010贵州铜仁）如图，MN为⊙O的弦，∠M＝30°，则∠MON等于（ ）‎ ‎ ‎ A．30° B．60° C．90° D．120°‎ ‎【答案】D ‎ ‎49．（2010黑龙江绥化）如图，⊙O是△ABC的外接圆，AD是⊙O的直径，若⊙O的半径为6，sinB=，则线段AC的长是（ ）‎ A.3 B‎.4 ‎ C.5 D.6‎ ‎【答案】B ‎ ‎50．（2010广东湛江）如图，已知圆心角∠BOC＝100°，则圆周角∠BAC的大小是（ ）‎ A. 50° B. 100° C.130 ° D. 200° ‎ ‎【答案】A ‎ ‎51．（2010广东清远）下列各图中，∠1=∠2的是（ ）‎ ‎【答案】D ‎ ‎52．（2010内蒙呼和浩特）如图，⊙O的直径CD＝‎10cm，AB是⊙O的弦，AB CD，垂足为M，OM：OC＝3：5，则AB的长为( )‎ A．‎8cm B.cm C‎.6cm D‎.2cm ‎【答案】A ‎ ‎53．（2010四川攀枝花）如图２，△ABC内接于⊙O，若∠OAＢ＝２８，则∠C的大小是（ ）‎ A．５６ 　　B．６‎２‎ 　　C．２８　　　　D．３２ ‎ B C A O 图2‎ ‎ 全品中考网 ‎【答案】B ‎ 二、填空题 ‎1．1．(2010江苏苏州)如图，已知A、B两点的坐标分别为、(0，2)，P是△AOB外接圆上的一点，且∠AOP=45°，则点P的坐标为 ▲ ．‎ ‎【答案】‎ ‎2．（2010安徽省中中考） 如图，△ABC内接于⊙O，AC是⊙O的直径，∠ACB＝500，点D是BAC上一点，则∠D＝_______________‎ ‎【答案】‎ ‎3．（2010安徽芜湖）芜湖国际动漫节期间，小明进行了富有创意的形象设计．如图1，他在边长为1的正方形ABCD内作等边三角形BCE，并与正方形的对角线交于F、G点，制成如图2的图标． 则图标中阴影部分图形AFEGD的面积＝__________．‎ ‎【答案】‎ ‎4．（10湖南益阳）1如图5，分别以A、B为圆心，线段AB的长为半径的两个圆相交于C、D两点，则∠CAD的度数为　　　．‎ ‎【答案】120°‎ ‎5．（2010山东青岛）如图，点A、B、C在⊙O上，若∠BAC = 24°，则∠BOC = °．‎ O A B C 第10题图 ‎·‎ ‎【答案】48‎ ‎6．（2010山东威海）如图，AB为⊙O的直径，点C，D在⊙O上．若 ‎∠AOD＝30°，则∠BCD的度数是 ． ‎ ‎﹙第14题图﹚‎ A B D O C ‎【答案】105°‎ ‎7．（2010四川眉山）如图，∠A是⊙O的圆周角，∠A=40°，则∠OBC的度数为_______．‎ ‎【答案】50°‎ ‎8．（2010重庆綦江县）如图所示，A、B、C、D是圆上的点，∠1＝68°，∠A＝40°．则∠D＝_______．‎ ‎【答案】28°‎ ‎9．（2010浙江绍兴）如图,⊙O是正三角形的外接圆,点在劣弧上,‎ ‎ =22°,则的度数为_____________.‎ 第12题图 ‎【答案】38°‎ ‎10．（2010 浙江衢州） 如图，△ABC是⊙O的内接三角形，点D是的中点，‎ 已知∠AOB=98°，∠COB=120°．则∠ABD的度数是　　　　　　．‎ A B C D O ‎(第16题)‎ ‎【答案】101°‎ ‎11．（2010江苏泰州）如图⊙O的半径为‎1cm，弦AB、CD的长度分别为，则弦AC、BD所夹的锐角＝ ．‎ ‎【答案】75°‎ ‎ 12．（2010江苏无锡）如图，AB是O的直径，点D在O上∠AOD=130°，BC∥OD交O于C，则∠A= ▲ ．‎ ‎（第15题）‎ ‎【答案】40°‎ ‎13．（2010湖南邵阳）如图（八）在等边△ABC中，以AB为直径的⊙O与BC相交于点D，连结AD，则∠DAC的度数为 ．‎ ‎ 图（八）‎ ‎【答案】）30°‎ ‎14．（2010 江苏连云港）如图，点A、B、C在⊙O上，AB∥CD，∠B＝22°，则∠A＝________‎ ‎°．‎ AD BAD O ‎·‎ CFEBAD 第16题 ‎【答案】44‎ ‎15．（2010 黄冈）如图，⊙O中，的度数为320°，则圆周角∠MAN＝____________.‎ ‎　　　　　　　　　　‎ ‎　　　第4题图　　　　　　　　　　　　　　‎ ‎【答案】20°‎ ‎16．（2010福建宁德）如图，在直径AB＝12的⊙O中，弦CD⊥AB于M，且M是半径OB的中点，‎ 则弦CD的长是_______（结果保留根号）.‎ ‎·‎ A B C D O M 第17题图 ‎【答案】6‎ ‎17．（2010江西）如图，以点P为圆心的圆弧与X轴交于A，B；两点，点P的坐标为（4，2）点A的坐标为（2，0）则点B的坐标为 ．‎ ‎（15题）‎ ‎【答案】‎ ‎18．（2010年贵州毕节）如图，AB为⊙O的弦，⊙O的半径为5，OC⊥AB于点D，交⊙O于点C，且CD＝l，则弦AB的长是 ．‎ ‎【答案】6． ‎ ‎19．（2010 四川巴中）如图7所示，⊙O的两弦AB、CD交于点P，连接AC、BD，‎ 得S△ACP：S△DBP=16:9，则AC：BD ‎ ‎ ‎ ‎【答案】4：3。‎ ‎20．（2010浙江湖州）请你在如图所示的12×12的网格图形中任意画一个圆，则所画的圆最多能经过169个格点中的 个格点．‎ ‎【答案】12．‎ ‎21．（2010江苏常州）如图，AB是⊙O的直径，弦DC与AB相交于点E，若∠ACD=60°，∠ADC=50°，则 ‎∠ABD= ，∠CEB= 。‎ ‎【答案】60°，100°‎ ‎22．（2010江苏淮安）如图，已知点A，B，C在⊙O上，AC∥0B，∠BOC=40°，则∠ABO= ．‎ ‎【答案】20°‎ ‎23．（2010湖北荆门）在⊙O中直径为4，弦AB=2，点C是圆上不同于A、B的点，那么∠ACB的度数为________． ‎ ‎【答案】60°或120°‎ ‎24．（2010 四川成都）如图，在中，为⊙O的直径，，‎ 则的度数是_____________度．‎ ‎【答案】100‎ ‎25．（2010 四川成都）如图，内接于⊙O，，是⊙O上与点关于圆心成中心对称的点，是边上一点，连结．已知，，是线段上一动点，连结并延长交四边形的一边于点，且满足，则 的值为_______________．‎ ‎【答案】1和 ‎26．（2010湖北鄂州）已知⊙O的半径为10，弦AB的长为，点C在⊙O上，且C点到弦AB所在的直线的距离为5，则以O、A、B、C为顶点的四边形的面积是 ．‎ ‎【答案】‎ ‎27．（2010江苏扬州）如图，AB为⊙O直径，点C、D在⊙O上，已知∠BOC＝70°，AD∥OC，则∠AOD＝__________．‎ A B C D O 第15题 ‎【答案】40‎ ‎28．（2010北京）如图，AB为⊙O的直径，弦CD⊥ AB，垂足为点E，连结OC，若OC＝5，CD＝8，则AE＝ ．‎ ‎【答案】2‎ ‎29．（2010湖北随州）如图，⊙O中，的度数为320°，则圆周角∠MAN＝____________.‎ ‎　　　　　　　　　　‎ ‎　　　第4题图　　　　　　　　　　　　　‎ ‎【答案】20°‎ ‎30．（2010江苏徐州）如图，在以O为圆心的两个同心圆中，大圆的弦AB与小圆相切于点C，若大圆的半径为‎5 cm，小圆的半径为‎3 cm，则弦AB的长为_______cm．‎ ‎【答案】8‎ ‎31．（2010云南昆明）半径为r的圆内接正三角形的边长为 .（结果可保留根号）‎ ‎【答案】 r ‎ ‎32．（2010陕西西安）如图是一条水平铺设的直径为‎2米的通水管道横截面，其水面宽 为‎1.6米，则这条管道中此时最深为 米。‎ ‎【答案】0.4‎ ‎33．（2010江西省南昌）如图.⊙O 中，AB、AC是弦，O在∠ABO的内部，，，‎ ‎，则下列关系中，正确的是 （ ）‎ ‎ A. B. ‎ ‎ C． D. ‎ ‎【答案】‎ ‎34．（2010 福建三明）如图，在⊙O中，∠ACB=35°，则∠AOB= 度。‎ ‎【答案】10‎ ‎35．（2010 山东东营）将一直径为‎17cm的圆形纸片（图①）剪成如图②所示形状的纸片，再将纸片沿虚线折叠得到正方体（图③）形状的纸盒，则这样的纸盒体积最大为 cm3．‎ ‎（第16题图）‎ ‎①‎ ‎②‎ ‎③‎ ‎【答案】‎ ‎36．（2010 江苏镇江）如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，若AB=10，CD=8，则线段OE的长为 .‎ ‎【答案】3‎ ‎37．（2010 山东淄博）如图，在直角坐标系中，以坐标原点为圆心、半径为1的⊙O与x轴交于A，B两点，与y轴交于C，D两点．E为⊙O上在第一象限的某一点，直线BF交⊙O于点F，且∠ABF＝∠AEC，则直线BF对应的函数表达式为　　　　　　　　　　　． ‎ E B O A y x ‎(第17题)‎ C D ‎【答案】，‎ ‎38．（2010 云南玉溪） 如图6，在半径为10的⊙O 中，OC垂直弦AB于点D， ‎ AB＝16，则CD的长是 ．‎ ‎【答案】4‎ ‎39．（2010 天津）如图，⊙O中，弦、相交于点， 若，，则等于 ‎（A）‎ ‎（B）‎ ‎（C）‎ ‎（D）‎ 第（7）题 B C A D P O ‎【答案】C ‎ ‎40．（2010 广西钦州市）如图，点C在⊙O上，∠ACB＝50°，则∠AOB＝_▲_°．‎ ‎【答案】100°‎ ‎41．（2010吉林长春）如图，⊙P与x轴切与点O，点P的坐标为（0,1），点A在⊙P上，且在第一象限，∠APO=120°，⊙P沿x轴正方向滚动，当点A第一次落在x轴上时，点A的横坐标为 ‎ ‎（结果保留π）。‎ ‎【答案】x ‎ ‎42．（2010新疆乌鲁木齐）如图4，AB是⊙O的直径，C、D为⊙O上的两点，若°，则的度数为 。‎ ‎【答案】55°‎ ‎43．（2010广西南宁）如图6,为半圆的直径，,平分，交半 圆于点,交于点，则的度数是 ‎ ‎ ‎ ‎【答案】67.5‎ ‎44．（2010云南昭通）如图5，⊙O的弦AB=8， M是AB的中点，且OM为3，则⊙O的半径为________．‎ ‎【答案】5‎ ‎45．（2010贵州遵义）如图，⊿ABC内接于⊙O，∠C=40 ，则∠ABO=　　　度.‎ ‎【答案】50‎ ‎46．（2010广西柳州）如图8，AB是⊙O的直径，弦BC=‎2cm，F是弦BC的 中点，∠ABC=60°．若动点E以‎2cm/s的速度从A点 出发沿着A→B→A方向运动，设运动时间为t(s)(0≤t＜3)，‎ 连结EF，当t值为________s时，△BEF是直角三角形．‎ F E O A C B ‎【答案】1或1.75或2.25‎ ‎47．（2010辽宁本溪）如图所示，△ABC内接于⊙O，∠A=40°，则∠OBC的度数是 .‎ A C B O ‎【答案】50°‎ ‎48．（2010福建南平）如图，△ABC是⊙O的内接等边三角形，则∠BOC=_______°.‎ 第14题 A B C O ‎·‎ 答案:120‎ ‎49．（2010年福建省泉州）如图，点、、在⊙O上，，则 .‎ ‎【答案】90°‎ ‎50．（2010广东肇庆）如图2，点A、B、C都在⊙O上，若∠C＝35°，则∠AOB的度数是______度．‎ ‎ 全品中考网 ‎【答案】70°‎ ‎51．（2010四川广安）如右图，在⊙O中，点C是弧 的中点，∠A=50°，则∠BOC等于 度．‎ ‎【答案】40°‎ ‎52．（2010吉林）如图，AB是⊙O的直径，点C在⊙O上，∠ABC=500，动点P在弦BC上，则∠PAB可能为________度（写出一个符合条件的度数即可）。‎ ‎【答案】‎ ‎53．（2010四川达州）如图6，一个宽为‎2 cm的刻度尺在圆形光盘上移动，当刻 度尺的一边与光盘相切时，另一边与光盘边缘两个交点处的 读数恰好是“2”和“10”（单位：cm），那么该光盘的 直径是 cm.‎ 图6‎ ‎【答案】10‎ ‎54．（2010湖南娄底）如图7在半径为R的⊙O中，弦AB的长与半径R相等，C是优弧上一点，则∠ACB的度数是_______.‎ 图7‎ A B C O ‎·‎ ‎ ‎ ‎【答案】30°‎ ‎55．（2010内蒙赤峰）如图，AB是⊙O的一条弦，OD⊥AB，垂足为C，交 ‎⊙O于一点D，点E在⊙O上，∠AED=25°，则∠OBA 的度数是___________．‎ ‎【答案】40o ‎ ‎56．（2010湖北黄石）如图，⊙O中，OA⊥BC,∠AOB＝60°,则sin∠ADC＝ .‎ ‎【答案】‎ 三、解答题 ‎1．（2010甘肃兰州）（本题满分6分）小明家的房前有一块矩形的空地，空地上有三棵树A、B、C，小明想建一个圆形花坛，使三棵树都在花坛的边上．‎ ‎（1）（本小题满分4分）请你帮小明把花坛的位置画出来（尺规作图，不写作法，保留作图痕迹）．‎ ‎（2）（本小题满分2分））若△ABC中AB=‎8米，AC=‎6米，∠BAC=，试求小明家圆形花坛的面积．‎ ‎【答案】(1)（本小题满分4分）‎ 用尺规作出两边的垂直平分线 ‎ 作出圆 ⊙O即为所求做的花园的位置.（图略） ‎ ‎（2）（本小题满分2分）‎ ‎ 解：∵∠BAC=,AB=‎8米,AC=‎6米, ∴BC=‎‎10米 ‎ ∴ △ABC外接圆的半径为‎5米 ∴小明家圆形花坛的面积为2平方米 . ‎ ‎2．（2010江苏南通）（本小题满分8分） ‎ 如图，⊙O的直径AB垂直于弦CD，垂足P是OB的中点，‎ CD＝‎6 cm，求直径AB的长．‎ O B A D C ‎·‎ P ‎（第20题）‎ ‎【答案】方法一：连结OC，BC，则OC=OB ‎∵PC垂直平分OB，∴OC=BC.∴OC=OB=BC.∴△BOC为等边三角形.‎ ‎∴∠BOC=60° 由垂径定理，CP=CD=‎‎3cm 在Rt△BOC中，=tan∠COP= ∴OP=cm.‎ ‎∴AB=2OB=4OP=‎4‎cm.‎ 方法二：‎ 解：连OC，设OP为，则OC为2，直径AB为4，‎ 在Rt△COP中，‎ 即，解得 所以直径AB为cm.‎ ‎3．（2010山东济宁）如图，为外接圆的直径，，垂足为点，的平分线交于点，连接，.‎ ‎(1) 求证：； ‎ ‎(2) 请判断，，三点是否在以为圆心，以为半径的圆上？并说明理由.‎ ‎(第20题)‎ ‎【答案】‎ ‎（1）证明：∵为直径，，‎ ‎∴.∴. 3分 ‎（2）答：，，三点在以为圆心，以为半径的圆上. 4分 理由：由（1）知：，∴.‎ ‎∵，，，‎ ‎∴.∴. 6分 由（1）知：.∴.‎ ‎∴，，三点在以为圆心，以为半径的圆上. 7分 ‎4．（2010浙江嘉兴）如图，已知⊙O的半径为1，PQ是⊙O的直径，n个相同的正三角形沿PQ排成一列，所有正三角形都关于PQ对称，其中第一个的顶点与点P重合，第二个的顶点是与PQ的交点，…，最后一个的顶点、在圆上．‎ ‎（第23题）‎ ‎（第23题 图1）‎ ‎（第23题 图2）‎ ‎（1）如图1，当时，求正三角形的边长；‎ ‎（2）如图2，当时，求正三角形的边长；‎ ‎（3）如题图，求正三角形的边长（用含n的代数式表示）．‎ ‎【答案】‎ ‎（1）设与交于点D，连结，‎ ‎（第23题 图1）‎ 则，‎ 在中，，‎ 即，‎ 解得． …4分 ‎（第23题 图2）‎ ‎（2）设与交于点E，连结，‎ 则，‎ 在中，‎ 即，‎ 解得． …4分 ‎（第23题）‎ ‎（3）设与交于点F，连结，‎ 则，‎ 在中，‎ 即，‎ 解得． …4分 ‎5．（2010 嵊州市）（10分）‎ ‎（1）请在图①的正方形ABCD内，画出使∠APB＝90°的一个点P，并说明理由。‎ ‎（2）请在图②的正方形ABCD内（含边），画出使∠APB＝60°的所有的点P，并说明理由。‎ ‎（3）如图③，现在一块矩形钢板ABCD，AB＝4，BC＝3，工人师傅想用它裁出两块全等的、面积最大的△APB和△CPD钢板，且∠APB＝∠CPD＝60°，请你在图③中画出符合要求的点P和P。‎ ‎ 图① 图② 图③‎ ‎【答案】(1)如图①，点P为所求 ‎（2）如图②，圆上实线部分弧EF为所求②③‎ ‎（3）如图③，点、为所求 ‎6．（2010浙江金华）A C B D E F O 如图，AB是⊙O的直径，C是的中点，CE⊥AB于 E，BD交CE于点F．‎ ‎1‎ ‎2‎ ‎（1）求证：CF﹦BF；‎ ‎（2）若CD ﹦6， AC ﹦8，则⊙O的半径为 ▲ ， ‎ CE的长是 ▲ ．‎ ‎【答案】解：(1) 证明：∵AB是⊙O的直径，∴∠ACB﹦90°‎ ‎ 又∵CE⊥AB， ∴∠CEB﹦90°‎ ‎ ∴∠2﹦90°－∠A﹦∠1‎ ‎ 又∵C是弧BD的中点，∴∠1﹦∠A ‎ ∴∠1﹦∠2,‎ ‎ ∴ CF﹦BF﹒ ‎ A C B D E F O ‎1‎ ‎2‎ ‎(2) ⊙O的半径为5 ， CE的长是 ‎7．（2010 四川南充）如图，△ABC内接于⊙O，AD⊥BC，OE⊥BC， OE＝BC． （1）求∠BAC的度数． （2）将△ACD沿AC折叠为△ACF，将△ABD沿AB折叠为△ABG，延长FC和GB相交于点H．求证：四边形AFHG是正方形． （3）若BD＝6，CD＝4，求AD的长．‎ A F C D E G H B O ‎　　　‎A F C D E G H B O ‎【答案】（1）解：连结OB和OC． ‎A F C D E G H B O ‎∵　OE⊥BC，∴　BE＝CE． ∵　OE＝BC，∴　∠BOC＝90°，∴　∠BAC＝45°．　　　　　　　‎ ‎（2）证明：∵　AD⊥BC，∴　∠ADB＝∠ADC＝90°． 由折叠可知，AG＝AF＝AD，∠AGH＝∠AFH＝90°， ‎ ‎　　　　　　∠BAG＝∠BAD，∠CAF＝∠CAD，　　　　　　　　　 ∴　∠BAG＋∠CAF＝∠BAD＋∠CAD＝∠BAC＝45°． ∴　∠GAF＝∠BAG＋∠CAF＋∠BAC＝90°． ∴　四边形AFHG是正方形．　　　　　　　　　　　　　　　　　　 （3）解：由（2）得，∠BHC＝90°，GH＝HF＝AD，GB＝BD＝6，CF＝CD＝4． 设AD的长为x，则　BH＝GH－GB＝x－6，CH＝HF－CF＝x－4．　　 在Rt△BCH中，BH2＋CH2＝BC2，∴　（x－6）2＋（x－4）2＝102． 解得，x1=12，x2＝－2（不合题意，舍去）． ∴　AD＝12．　　　　　　　　　　　　　　　　　　　　　　　　‎ ‎8．（2010福建福州）如图，AB是⊙O的直径，弦CD⊥AB于点E，点P在⊙O上，∠1＝∠C．‎ ‎（1）求证：CB∥PD；‎ ‎（2）若BC＝3，sinP＝，求⊙O的直径．‎ ‎(第19题)‎ ‎【答案】解：（1）证明：∵ ， ∴ ∠C＝∠P．‎ 第19题图 ‎ 又∵ ∠1＝∠C， ∴ ∠1＝∠P．‎ ‎ ∴ CB∥PD．‎ ‎ （2）连接AC．‎ ‎ ∵ AB为0D的直径， ∴ ∠ACB=90°．‎ ‎ 又∵ CD⊥AB， ∴ ‎ ‎∴ ∠A＝∠P， ∴ sinA＝sinP．‎ 在Rt△ABC中， sinA＝，‎ ‎∵ sinP＝， ∴ ＝．‎ 又∵ BC＝3， ∴ AB＝5．‎ 即⊙O的直径为5．‎ ‎9．（2010邵阳）阅读下列材料，然后解答问题。‎ 经过正四边形（即正方形）各顶点的圆叫作这个正四边形的外接圆。圆心是正四边形的对称中心，这个正四边形叫作这个圆的内接正四边形。‎ 如图（十三），已知正四边形ABCD的外接圆⊙O，⊙O的面积为S，正四边形ABCD 的面积为S，以圆心O为顶点作∠MON，使∠MON=90°，将∠MON绕点O旋转，OM、ON分别与⊙O相交于点E、F，分别与正四边形ABCD的边相交于点G、H。设OE、OF、及正四边形ABCD的边围成的图形（图中阴影部分）的面积为S ‎（1）当OM经过点A时（如图①），则S、S、S之间的关系为：S＝ （用含S、S的代数式表示）；‎ ‎（2）当OM⊥AB时（如图②），点G为垂足，则（1）中的结论仍然成立吗？请说明理由。‎ ‎（3）当∠MON旋转到任意位置时（如图③，）则（1）中的结论仍然成立吗？请说明理由．‎ ‎ 图（十三）‎ ‎【答案】解：（1）‎ ‎（2）成立。理由：连OB，可证图中的两个阴影部分的面积之和等于图①的阴影部分的面积 ‎（3）成立。过点O分别作AB、BC的垂线交AB、BC于点P、Q，交圆于点X、Y，可证直角三角形OPG全等于直角三角形OQH，可说明两阴影部分面积之和等于图①的阴影部分面积．‎ ‎10．（2010年上海）机器人“海宝”在某圆形区域表演“按指令行走”，如图5所示，“海宝”从圆心O出发，先沿北偏西67.4°方向行走‎13米至点A处，再沿正南方向行走‎14米至点B处，最后沿正东方向行走至点C处，点B、C都在圆O上.（1）求弦BC的长；（2）求圆O的半径长.‎ ‎（本题参考数据：sin 67.4° = ，cos 67.4° = ，tan 67.4° = ）‎ 图5‎ ‎【答案】(1)过A作AH垂直NS于点H，∴∠AHO=90°, sin 67.4° = =,‎ ‎∵OA=‎13米,∴AH=‎12米,∵AB∥OS,记BC与OS交于点D，‎ ‎∴AH=BD=‎12米,∵OS⊥BC于点D，∴BD=CD=‎12米,∴BC=‎24米.‎ ‎（2）由（1）可得OH=‎5米，∵AB=‎14米，∴HD=‎9米，联接OB，‎ ‎∵∠ODB=90°,∴OB=‎ ‎11．（2010 广东珠海）如图，△ABC内接于⊙O，AB＝6,AC＝4,D是AB边上一点，P是优弧BAC的中点，连结PA、PB、PC、PD.‎ ‎(1)当BD的长度为多少时，△PAD是以AD为底边的等腰三角形？并证明；‎ ‎（2）若cos∠PCB=，求PA的长.‎ ‎【答案】解：（1）当BD＝AC＝4时，△PAD是以AD为底边的等腰三角形 ‎∵P是优弧BAC的中点 ∴弧PB＝弧PC ‎∴PB＝PC ‎∵BD＝AC＝4 ∠PBD=∠PCA ‎∴△PBD≌△PCA ‎∴PA=PD 即△PAD是以AD为底边的等腰三角形 ‎（2）由（1）可知，当BD＝4时，PD＝PA，AD＝AB-BD＝6-4＝2‎ 过点P作PE⊥AD于E，则AE＝AD=1‎ ‎∵∠PCB=∠PAD ‎∴cos∠PAD=cos∠PCB=‎ ‎∴PA=‎ ‎12．（2010湖北荆门）如图，圆O的直径为5，在圆O上位于直径AB的异侧有定点C和动点P，已知BC：CA=4：3，点P在半圆弧AB上运动（不与A、B两点重合），过点C作CP的垂线CD交PB的延长线于D点．‎ ‎（1）求证：AC·CD=PC·BC；‎ ‎（2）当点P运动到AB弧中点时，求CD的长；‎ ‎ （3）当点P运动到什么位置时，△PCD的面积最大？并求出这个最大面积S。‎ ‎【答案】（1）由题意，AB是⊙O的直径；∴∠ACB=90。，∵CD⊥CP，∴∠PCD=90。‎ ‎∴∠ACP+∠BCD=∠PCB+∠DCB=90。，∴∠ACP=∠DCB，又∵∠CBP=∠D+∠DCB，∠CBP=∠ABP+∠ABC，∴∠ABC=∠APC，∴∠APC＝∠D，∴△PCA∽△DCB；∴， 全品中考网 ‎∴AC·CD=PC·BC ‎（2）当P运动到AB弧的中点时,连接AP，∵AB是⊙O的直径，∴∠APB=90。，又∵P是弧AB的中点，∴弧PA=弧PB，∴AP=BP，∴∠PAB=∠PBA=45.,又AB=5，∴PA=，过A作AM⊥CP，垂足为M，在Rt△AMC中，∠ACM=45 ，∴∠CAM=45，∴AM=CM=，在Rt△AMP中，AM2+AP2=PM2，∴PM=，∴PC=PM+=。由（1）知：AC·CD=PC·BC ，3×CD=PC×4，∴CD＝‎ ‎（3）由（1）知：AC·CD=PC·BC，所以AC：BC=CP：CD；所以CP：CD=3：4，而△PCD的面积等于·=，CP是圆O的弦，当CP最长时，△PCD的面积最大，而此时CP就是圆O的直径；所以CP=5，∴3：4=5：CD；∴CD=，△PCD的面积等于·==；‎ ‎ ‎ ‎13．（2010 四川成都）已知：如图，内接于⊙O，为直径，弦于，是AD的中点，连结并延长交的延长线于点，连结，分别交、于点、．‎ ‎ （1）求证：是的外心；‎ ‎ （2）若,求的长；‎ ‎ （3）求证：．‎ ‎【答案】（1）证明：∵C是AD的中点，∴AC=CD，‎ ‎∴∠CAD=∠ABC‎⌒‎ ‎∵AB是⊙O的直径，∴∠ACB=90°。‎ ‎∴∠CAD+∠AQC=90°‎ 又CE⊥AB，∴∠ABC+∠PCQ=90°‎ ‎∴∠AQC=∠PCQ ‎⌒‎ ‎⌒‎ ‎∴在△PCQ中，PC=PQ，‎ ‎⌒‎ ‎⌒‎ ‎∵CE⊥直径AB，∴AC=AE ‎∴AE=CD ‎∴∠CAD=∠ACE。‎ ‎∴在△APC中，有PA=PC，‎ ‎∴PA=PC=PQ ‎∴P是△ACQ的外心。‎ ‎（2）解：∵CE⊥直径AB于F，‎ ‎∴在Rt△BCF中，由tan∠ABC=，CF=8，‎ 得。‎ ‎∴由勾股定理，得 ‎∵AB是⊙O的直径，‎ ‎∴在Rt△ACB中，由tan∠ABC=，‎ ‎ 得。‎ 易知Rt△ACB∽Rt△QCA，∴‎ ‎∴。‎ ‎（3）证明：∵AB是⊙O的直径，∴∠ACB=90°‎ ‎∴∠DAB+∠ABD=90°‎ 又CF⊥AB，∴∠ABG+∠G=90°‎ ‎∴∠DAB=∠G；‎ ‎∴Rt△AFP∽Rt△GFB，‎ ‎∴，即 易知Rt△ACF∽Rt△CBF，‎ ‎∴‎ ‎∴‎ 由（1），知PC=PQ，∴FP+PQ=FP+PC=FC ‎∴。‎ ‎14．（2010山东潍坊）如图，AB是⊙O的直径，C、D是⊙O上的两点，且AC＝CD．‎ ‎（1）求证：OC∥BD；‎ ‎（2）若BC将四边形OBDC分成面积相等的两个三角形，试确定四边形OBDC的形状．‎ ‎【答案】（1） ⊙O中，AC＝CD，则∠ABC＝∠DBC，∵OC＝OB，则∠ABC＝∠OAB，∴∠OCB＝∠DBC，则OC∥BD；‎ ‎（2）∵OC∥BD，不妨设平行线OC与BD之间的距离为h，又S△OBC＝OC×h，S△OBC＝OC×h，∵BC将四边形OBDC分成面积相等的两个三角形，即S△OBC＝ S△DBC，则OC＝BD，∴四边形OBDC为平行四边形，因为OC＝OB，所以四边形OBDC为菱形．‎ ‎15．（2010广东中山）如图，PA与⊙O相切于A点，弦AB⊥OP，垂足为C，OP与⊙O相交于D点，已知OA=2，OP=4．‎ ‎（1）求∠POA的度数；‎ ‎（2）计算弦AB的长．‎ ‎【答案】解：（1）∵PA与⊙O相切于A点，‎ ‎∴∠PAO=‎ 在RtΔPAO中，OA=2，OP=4‎ ‎∴∠POA=‎ ‎（2）∵AB⊥OP ‎∴AC=BC，∠OCA=‎ 在RtΔAOC中，OA=2，∠AOC=‎ ‎∴AC=‎ ‎∴AB=2‎ ‎16．（2010黑龙江哈尔滨）如图，AB、AC为⊙‎ O的弦，连接CO、BO并延长分别交弦AB、AC于点E、F，∠B=∠C。‎ 求证：CE=BF。‎ ‎【答案】证明：∵OB、OC是⊙O的半径，∴OB=OC ‎ 又 ‎ ‎≌ ‎ ‎∴OE=OF ∴CE=BF ‎ ‎17．（2010四川 泸州）(本题满分10分)如图9,在平行四边形ABCD中,E为BC边上的一点,且AE与DE分别平分∠BAD和∠ADC.‎ (1) 求证:AE⊥DE;‎ (2) 设以AD为直径的半圆交AB于F,连接DF交AE于G,已知CD=5,AE=8,求的值.‎ ‎【答案】(1)证明:在平行四边形ABCD中,AB∥CD,∴∠BAD+∠ADC=180°, ‎ 又∵AE、DE平分∠BAD、∠ADC， ‎ ‎∴∠DAE+∠ADE=90°， ‎ ‎∴∠AED＝90°， ‎ ‎∴AE⊥DE. ‎ ‎(2)解:在平行四边形ABCD中,AD∥BC,AB=CD=5,AD=BC,‎ ‎∴∠DAE=∠BEA, ‎ 又∵∠DAE=∠BAE,∴∠BEA=∠BAE,‎ ‎∴BE=AB=5, ‎ 同理EC=CD=5, ‎ ‎∴AD=BC=BE+EC=10, ‎ 在RtAED中,‎ DE===6, ‎ 又∵AD为半圆的直径,∴∠AFD=90°,∴∠AFD=∠AED,‎ ‎∵∠DAE=∠FAG,∴AFG∽AED, ‎ ‎∴. ‎ ‎18．（2010吉林长春）‎ 第16届亚运会将在中国广州举行。小李预定了两种价格的亚运会门票，其中甲种门票共花费280元，乙种门票共花费300元，甲种门票比乙种门票多2张，乙种门票价格是甲种门票价格的1.5倍，求甲种门票的价格。‎ ‎【答案】‎ ‎18．（2010吉林长春）如图，将一个两边都带有刻度的直尺放在半圆形纸片上，使其一边经过圆心O，另一边所在直线与半圆相交于点D、E，量出半径OC=‎5cm，弦DE=‎8cm。求直尺的宽。‎ ‎【答案】‎ ‎19．（2010湖北宜昌）如图①，P是△ABC边AC上的动点，以P为顶点作矩形PDEF，顶点D,E在边BC上，顶点F在边AB上；△ABC的底边BC及BC上的高的长分别为a , h,且是关于x的一元二次方程的两个实数根，设过D,E,F三点的⊙O的面积为,矩形PDEF的面积为。‎ ‎（1）求证：以a+h为边长的正方形面积与以a、h为边长的矩形面积之比不小于4；‎ ‎（2）求的最小值；‎ ‎（3）当的值最小时，过点A作BC的平行线交直线BP与Q，这时线段AQ的长与m , n , k的取值是否有关？请说明理由。（11分）‎ A C B ‎(第23题)‎ 解：解法一：‎ ‎（1）据题意，∵a+h=.‎ ‎∴所求正方形与矩形的面积之比： ‎ ‎ 1分 由知同号, ‎ ‎ 2分 ‎（说明:此处未得出只扣1分, 不再影响下面评分）‎ ‎ 3分 即正方形与矩形的面积之比不小于4.‎ ‎（2）∵∠FED=90º,∴DF为⊙O的直径.‎ ‎⊙‎ ‎∴⊙O的面积为：． 4分 矩形PDEF的面积：．‎ ‎⊙‎ ‎∴面积之比： 设 ‎⊙‎ ‎……………………………………………………………6分 ‎, ‎ ‎⊙‎ ‎，即时（EF=DE）, 的最小值为 7分 ‎⊙‎ ‎（3）当的值最小时，这时矩形PDEF的四边相等为正方形．‎ 过B点过BM⊥AQ，M为垂足，BM交直线PF于N点，设FP＝ e，‎ ‎∵BN∥FE，NF∥BE,∴BN=EF,∴BN =FP =e.‎ 由BC∥MQ,得：BM =AG =h.‎ ‎∵AQ∥BC, PF∥BC, ∴AQ∥FP,‎ ‎∴△FBP∽△ABQ. 8分 M N ‎（说明：此处有多种相似关系可用，要同等分步骤评分）‎ ‎∴,……9分 ‎∴.∴……10分 ‎……11分 ‎∴线段AQ的长与m，n，k的取值有关. ‎ ‎（解题过程叙述基本清楚即可）‎ 解法二：‎ ‎（1）∵a，h为线段长，即a，h都大于0，‎ ‎　∴ah＞０…………1分（说明:此处未得出只扣1分,再不影响下面评分）‎ ‎ ∵（a-h）２≥０，当a＝h时等号成立.‎ ‎　　　　 故，（a-h）２＝（a＋h）２－‎４a h≥０． 2分 ‎　　　　∴（a＋h）２≥‎４a h，‎ ‎　　　　∴≥４．（﹡） 3分 ‎　　　　　　这就证得≥４．（叙述基本明晰即可）‎ ‎（2）设矩形PDEF的边PD=x，DE=y，则⊙O的直径为 .‎ ‎ S⊙O=…………4分, S矩形PDEF=xy ‎⊙‎ ‎= ‎ ‎= 6分 由（1）（*）， .‎ ‎.‎ ‎⊙‎ ‎∴的最小值是 7分 ‎⊙‎ ‎（3）当的值最小时，‎ 这时矩形PDEF的四边相等为正方形. ‎ ‎∴EF=PF．作AG⊥BC，G为垂足.‎ ‎∵△AGB∽△FEB，∴.……8分 ‎∵△AQB∽△FPB, ，……9分 ‎∴=．‎ 而 EF=PF，∴AG=AQ=h, ……………10分 ‎∴AG=h＝,‎ 或者AG=h＝ 11分 ‎∴线段AQ的长与m，n，k的取值有关.‎ ‎20．（2010福建省南平）如图，⊙O的直径AB长为6，弦AC长为2，∠ACB的平分线交⊙O于点D，求四边形ADBC的面积.‎ ‎·‎ 第21题 A B C O D ‎【答案】解：∵AB是直径， ∴∠ACB=∠ADB=90°，‎ 在Rt△ABC中，AB=6， AC= 2，∴BC=== 4 ‎∵∠ACB的平分线交⊙O于点D，∴∠DAC=∠BCD ‎∴=， ∴AD=BD ‎∴在Rt△ABD中，AD=BD= AB=3 ‎∴四边形ADBC的面积=S△ABC+S△ABD=AC·BC+AD·BD ‎=×2×4+×(3)2 =9+4 ‎21．（2010广西河池）如图10，为的直径，为弦，且，垂足为．‎ ‎（1）如果的半径为4，，求的度数；‎ ‎（2）若点为的中点，连结，．求证：平分；‎ ‎（3）在（1）的条件下，圆周上到直线距离为3的点有多少个？并说明理由．‎ A B D E O C H ‎【答案】解：（1）∵ AB为⊙O的直径，CD⊥AB ∴ CH＝CD＝2 ‎ A B D E O C H ‎　　　　　　在Rt△COH中，sin∠COH==‎ ‎ ∴ ∠COH=60° ‎ ‎ ∵ OA=OC ∴∠BAC=∠COH=30°　‎ ‎ （2）∵ 点E是的中点 ∴OE⊥AB ∴ OE∥CD ∴ ∠ECD=∠OEC 又∵ ∠OEC=∠OCE ‎∴ ∠OCE=∠DCE ‎ ‎∴ CE平分∠OCD ‎ ‎ 　（3）圆周上到直线的距离为3的点有2个. ‎ ‎ 因为劣弧上的点到直线的最大距离为2， 上的点到直线AC的最大距离为6，，根据圆的轴对称性，到直线AC距离为3的点有2个. ‎ ‎22．（2010广东清远）如下图，在⊙O中，点P在直径AB上运动，但与A、B两点不重合，过点P作弦CE⊥AB，在上任取一点D，直线CD与直线AB交于点F，弦DE交直线AB于点M，连接CM.‎ ‎（1）如图10，当点P运动到与O点重合时，求∠FDM的度数.‎ 图10 图11 图12‎ C A B ‎(P)‎ E O M F D C A B P E O F D M O C A B P E F D M ‎（2）如图11、图12，当点P运动到与O点不重合时，求证：FM·OB=DF·MC.‎ ‎【答案】28.　解：（1）点P与点O重合时，（如图10）‎ ‎∵CE是直径，∴∠CDE＝90°.…………（1分）‎ ‎∵∠CDE＋∠FDM＝180°，∴∠FDM＝90°.…………（2分）‎ ‎（2）当点P在OA上运动时（如图11）‎ ‎∵OP⊥CE，∴＝＝，CP＝EP.‎ ‎∴CM＝EM.　∴∠CMP＝∠EMP.‎ ‎∵∠DMO＝∠EMP，　∴∠CMP＝∠DMO.‎ ‎∵∠CMP＋∠DMC＝∠DMO＋∠DMC，‎ ‎∴∠DMF＝∠CMO. …………（3分）‎ ‎∵∠D所对的弧是，∠COM所对的弧是，‎ ‎∴∠D＝∠COM. …………（4分）‎ ‎∴△DFM∽△OCM.　∴＝ ‎∴FM·OC＝DF·MC.‎ ‎∵OB＝OC，　∴FM·OB＝DF·MC. …………（5分）‎ 当点P在OB上运动时，（如图12）‎ 证法一：连结AC，AE.‎ ‎∵OP⊥CE，∴＝＝，CP＝EP.‎ ‎∴CM＝EM，　∴∠CMO＝∠EMO.‎ ‎∵∠DMF＝∠EMO，　∴∠DMF＝∠CMO.………………（6分）‎ ‎∵∠CDE所对的弧是，∠CAE所对的弧是.‎ ‎∴∠CDE＋∠CAE＝180°.‎ ‎∴∠CDM＋∠FDM＝180°，∴∠FDM＝∠CAE.‎ ‎∵∠CAE所对的弧是，∠COM所对的弧是，‎ ‎∴∠CAE＝∠COM.‎ ‎∴∠FDM＝∠COM. ………………（7分）‎ ‎∴△DFM∽△OCM.　∴＝.‎ ‎∴FM·OC＝DF·MC.‎ ‎∵OB＝OC，　∴FM·OB＝DF·MC. ………………（8分）‎ 证法二：∵OP⊥CE，‎ ‎∴＝＝，＝＝，CP＝EP.‎ ‎∴CM＝EM，　∴∠CMO＝∠EMO.‎ ‎∵∠DMF＝∠EMO，　∴∠DMF＝∠CMO.………………（6分）‎ ‎∵∠CDE所对的弧是，‎ ‎∴∠CDE＝度数的一半＝的度数＝180°－的度数.‎ ‎∴∠FDM＝180°－∠CDE＝180°－（180°－的度数）＝的度数.‎ ‎∵∠COM＝的度数.‎ ‎∴∠FDM＝∠COM. ………………（7分）‎ ‎∴△DFM∽△OCM.　∴＝.‎ ‎∴FM·OC＝DF·MC.‎ ‎∵OB＝OC，　∴FM·OB＝DF·MC. ………………（8分）‎