中考专题折叠问题 18页

‎2016年中考专题：折叠问题 折叠型问题是近年中考的热点问题，通常是把某个图形按照给定的条件折叠，通过折叠前后图形变换的相互关系来命题。折叠型问题立意新颖，变幻巧妙，对培养学生的识图能力及灵活运用数学知识解决问题的能力非常有效。‎ 图形折叠问题中题型的变化比较多，主要有以下几点：‎ ‎1．图形的翻折部分在折叠前和折叠后的形状、大小不变，是全等形；‎ ‎2．图形的翻折部分在折叠前和折叠后的位置关于折痕成轴对称；‎ ‎3．将长方形纸片折叠，三角形是否为等腰三角形；‎ ‎4．解决折叠问题时，要抓住图形之间最本质的位置关系，从而进一步发现其中的数量关系；‎ ‎5．充分挖掘图形的几何性质，将其中的基本的数量关系，用方程的形式表达出来，并迅速求解，这是解题时常用的方法之一。‎ 折叠问题数学思想：‎ ‎(1)思考问题的逆向(反方向)，‎ ‎(2)从一般问题的特例人手，寻找问题解决的思路；‎ ‎(3)把一个复杂问题转化为解决过的基本问题的转化与化归思想；‎ ‎(4)归纳与分类的思想(把折纸中发现的诸多关系归纳出来，并进行分类)；‎ ‎(5)从变化中寻找不变性的思想.用“操作”、“观察”、“猜想”、“分析”的手段去感悟几何图形的性质是学习几何的方法。‎ 折叠问题主要有以下题型：‎ 题型1：动手问题 此类题目考查学生动手操作能力，它包括裁剪、折叠、拼图，它既考查学生的动手能力，又考查学生的想象能力，往往与面积、对称性质联系在一起．‎ 题型2：证明问题 动手操作的证明问题，既体现此类题型的动手能力，又能利用几何图形的性质进行全等、相似等证明．‎ 题型3：探索性问题 此类题目常涉及到画图、测量、猜想证明、归纳等问题，它与初中代数、几何均有联系．此类题目对于考查学生注重知识形成的过程，领会研究问题的方法有一定的作用，也符合新课改的教育理论。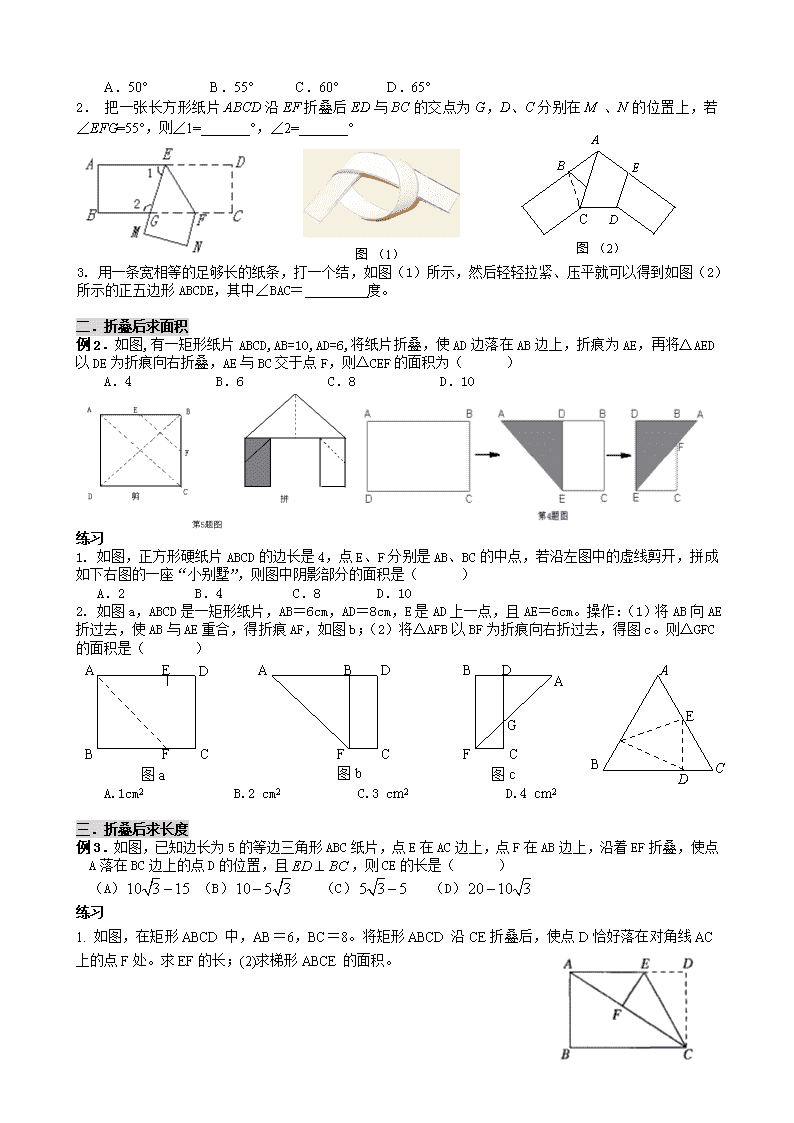 ‎ 典型例题 一．折叠后求度数 例1．将一张长方形纸片按如图所示的方式折叠，BC、BD为折痕，则∠CBD的度数为（ ）‎ A．600 B．750 C．900 D．950‎ ‎ ‎ 练习 ‎1．如图，把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置，若∠EFB＝65°，则∠AED′等于（ 　）‎ A．50° B．55°　　　C．60° D．65°‎ C D E B A 图 （2）‎ ‎2． 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G，D、C分别在M 、N的位置上，若∠EFG=55°，则∠1=_______°，∠2=_______°‎ 图 （1）‎ ‎3. 用一条宽相等的足够长的纸条，打一个结，如图（1）所示，然后轻轻拉紧、压平就可以得到如图（2）所示的正五边形ABCDE，其中∠BAC＝　 　度。‎ 二．折叠后求面积 例2．如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠，使AD边落在AB边上，折痕为AE，再将△AED以DE为折痕向右折叠，AE与BC交于点F，则△CEF的面积为（ 　　）‎ A．4 B．6 C．8 D．10‎ 练习 ‎1. 如图，正方形硬纸片ABCD的边长是4，点E、F分别是AB、BC的中点，若沿左图中的虚线剪开，拼成如下右图的一座“小别墅”，则图中阴影部分的面积是（ ）‎ A．2 B．4 C．8 D．10‎ A B C D E E A A A B B B C C C G D D D F F F 图a 图b 图c ‎2. 如图a，ABCD是一矩形纸片，AB＝6cm，AD＝8cm，E是AD上一点，且AE＝6cm。操作：（1）将AB向AE折过去，使AB与AE重合，得折痕AF，如图b；（2）将△AFB以BF为折痕向右折过去，得图c。则△GFC的面积是（ ）‎ A.1cm2 B.2 cm2 C.3 cm2 D.4 cm2‎ 三．折叠后求长度 例3．如图，已知边长为5的等边三角形ABC纸片，点E在AC边上，点F在AB边上，沿着EF折叠，使点A落在BC边上的点D的位置，且，则CE的长是（ ）‎ ‎（A） （B） （C） （D）‎ 练习 ‎1. 如图，在矩形ABCD中，AB＝6，BC＝8。将矩形ABCD沿CE折叠后，使点D恰好落在对角线AC上的点F处。求EF的长；(2)求梯形ABCE的面积。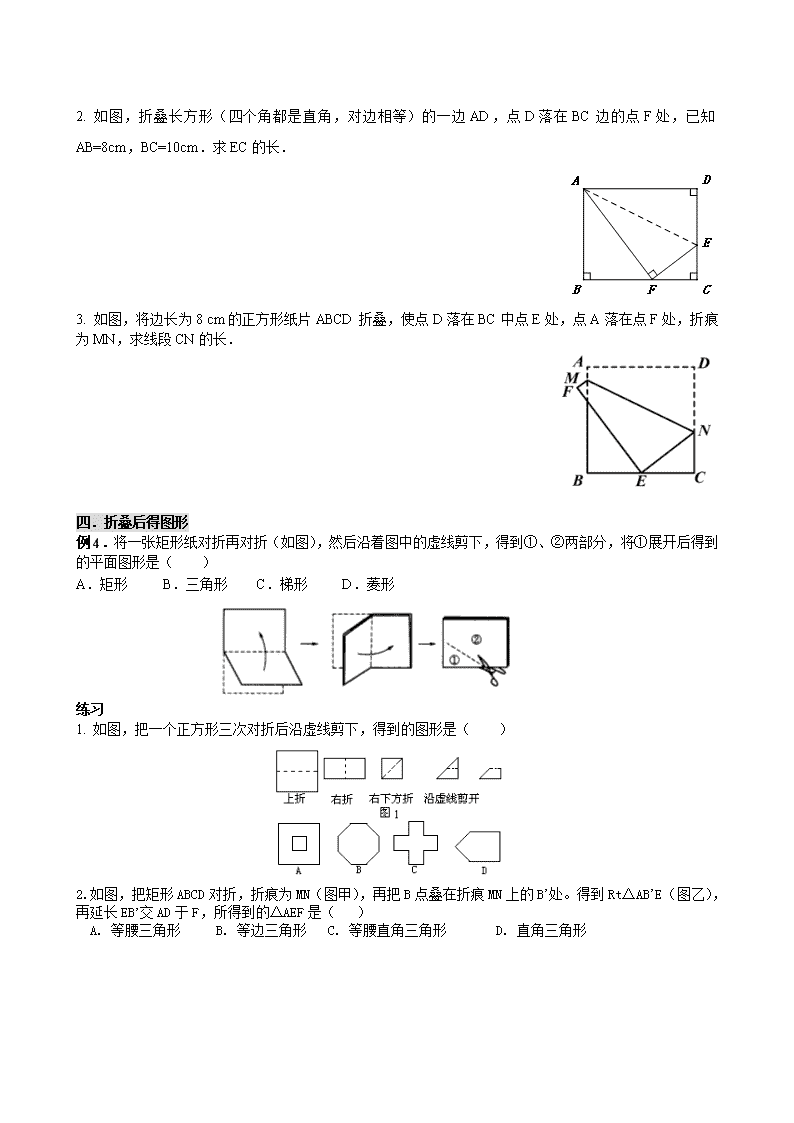‎ ‎2. 如图，折叠长方形（四个角都是直角，对边相等）的一边AD，点D落在BC边的点F处，已知AB=8cm，BC=10cm．求EC的长．‎ ‎3. 如图，将边长为8 cm的正方形纸片ABCD折叠，使点D落在BC中点E处，点A落在点F处，折痕为MN，求线段CN的长．‎ ‎ ‎ 四．折叠后得图形 例4．将一张矩形纸对折再对折（如图），然后沿着图中的虚线剪下，得到①、②两部分，将①展开后得到的平面图形是（ ）‎ A．矩形 B．三角形 C．梯形 D．菱形 练习 ‎1. 如图，把一个正方形三次对折后沿虚线剪下，得到的图形是（ ）‎ ‎2. 如图，把矩形ABCD对折，折痕为MN（图甲），再把B点叠在折痕MN上的B’处。得到Rt△AB’E（图乙），再延长EB’交AD于F，所得到的△AEF是（ ）‎ A. 等腰三角形 B. 等边三角形 C. 等腰直角三角形 D. 直角三角形 ‎3. 如图，已知BC为等腰三角形纸片ABC的底边，AD⊥BC，AD=BC. 将此三角形纸片沿AD剪开，得到两个三角形，若把这两个三角形拼成一个平面四边形，则能拼出互不全等的四边形的个数是（ ）‎ A. 2 B. 3 C. 4 D. 5‎ 五．折叠后得结论 例5．把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，则∠A与∠1+∠2之间有一种数量关系始终保持不变，请试着找一找这个规律，你发现的规律是（ ）‎ A. ∠A=∠1+∠2 B. 2∠A=∠1+∠2‎ C. 3∠A=2∠1+∠2 D. 3∠A=2(∠1+∠2)‎ 练习 ‎1. 从边长为a的正方形内去掉一个边长为b的小正方形(如图1)，然后将剩余部分剪拼成一个矩形(如图2)，上述操作所能验证的等式是（ ） A.a2–b2 =(a+b)(a-b)Ｂ.(a–b)2 = a2–2ab+ b2Ｃ.(a+b)2 = a2 +2ab+ b2 Ｄ.a2 +ab = a(a+b) ‎ ‎2. 如图，一张矩形报纸ABCD的长AB＝a cm，宽BC＝b cm，E、F分别是AB、CD的中点，将这张报纸沿着直线EF对折后，矩形AEFD的长与宽之比等于矩形ABCD的长与宽之比，则a∶b等于（ 　）　‎ A． B． C． D．‎ ‎（1）‎ ‎（2）‎ 六．折叠和剪切的综合应用 例6．在一张长12cm、宽5cm的矩形纸片内，要折出一个菱形.李颖同学按照取两组对边中点的方法折出菱形EFGH（见方案一），张丰同学沿矩形的对角线AC折出∠CAE=∠DAC，∠ACF=∠ACB的方法得到菱形AECF（见方案二），请你通过计算，比较李颖同学和张丰同学的折法中，哪种菱形面积较大？‎ A D E H F B C G ‎（方案一）‎ A D E F B C ‎（方案二）‎ 练习 ‎1. 已知如图，矩形ABCD中（图1），AD>AB，O为对角线的交点，过O作一直线分别交于BC、AD于N、M。‎ ‎（1）求证：梯形ABNM的面积等于梯形CDMN的面积；‎ ‎（2）如图2，当MN满足什么条件时，将矩形ABCD以MN为折痕，翻折后能使C点恰好与A点重合？（只写出满足的条件，不要求证明）‎ ‎（3）在（2）的条件下，若翻折后重叠部分的面积是总覆盖部分面积的一半，求BN：NC的值。‎ A C B D O x y ‎2. 如图，矩形AOBC，以O为坐标原点，OB、OA分别在x轴、y轴上，点A坐标为（0，3），∠OAB=‎ ‎60°，以AB为轴对折后，使C点落在点D处，求D点坐标。‎ ‎3．图①是由五个边长都是1的正方形纸片拼接而成的，过点A1的直线分别与BC1、BE交于点M、N，且图①被直线MN分成面积相等的上、下两部分．‎ ‎⑴ 求的值；‎ ‎⑵ 求MB、NB的长；‎ ‎⑶ 图①沿虚线折成一个无盖的正方体纸盒（图②）后，‎ 求点M、N间的距离． ‎ ‎4. 将一矩形纸片OABC放在平面直角坐标系中，O(0,0)，A(6,0)，C(0,3)．动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动，运动秒时，动点P从点A出发以相等的速度沿AO向终点O运动．当其中一点到达终点时，另一点也停止运动．设点P的运动时间为t（秒）．‎ ‎ （1）用含的代数式表示OP，OQ；‎ ‎ （2）当时，如图1，将△OPQ沿PQ翻折，点O恰好落在CB边上的点D处，求点D的坐标；‎ ‎ （3）连结AC，将△OPQ沿PQ翻折，得到△EPQ，如图2．问：PQ与AC能否平行？PE与AC能否垂直？若能，求出相应的t值；若不能，说明理由．‎ 图1‎ O P A x B D C Q y 图2‎ O P A x B C Q y E 巩固练习 ‎1、如图所示，有一块直角三角形纸片，，，，将斜边翻折，使点落在直角边的延长线上的点处，折痕为，则的长为 .‎ ‎2、如图，一圆柱高8cm，底面半径2cm，一只蚂蚁从点A爬到点B处吃食，要爬行的最短路程（取3）是 ．‎ ‎3、矩形纸片ABCD中，AD=4cm，AB=10cm，按如图18-1方式折叠，使点B与点D重合，折痕为EF，则DE=_______cm．‎ B D C A E ‎ ‎ ‎1题 2题 3题 5题 ‎4、在中，为边上的点，联结．如果将沿直线翻折后，点恰好落在边的中点处，那么点到的距离是 ．‎ ‎5、如图，在一块砖宽AN＝5cm，长ND＝10cm，CD上的点B距地面BD＝8cm，地面上A处的一只蚂蚁到B处吃食，需要爬行的最短路径是 。‎ G D A B C ‎6、如图，折叠矩形纸片ABCD，先折出折痕（对角线）BD，再折叠，使AD落在对角线BD上，得折痕DG，若AB = 2，BC = 1，求AG.‎ ‎7、如图，把矩形纸片ABCD沿对角线AC折叠，点B落在点E处，EC与AD相交于点F.‎ ‎（1）求证：△FAC是等腰三角形；‎ ‎（2）若AB=4，BC=6，求△FAC的周长和面积.‎ ‎8、如图，将矩形沿直线折叠，顶点恰好落在边上点处，已知，，求的长．‎ ‎9、矩形纸片ABCD的边长AB=4，AD=2．将矩形纸片沿EF折叠，使点A与点C重合，折叠后在其一面着色（如图），求着色部分的面积。‎ A B C D E G F F ‎10、如图，在边长为2的菱形ABCD中，∠B=450，AE为BC边上的高，将ΔABE沿AE所在直线翻折得ΔAB1E，求ΔAB1E与四边形AECD重叠部分的面积。‎ ‎11、如图、在矩形ABCD中，AB=6，CB=8，将矩形沿对角线BD折叠，点C落在C1处，再将所得图形对折，使点D与点A重合，设折痕为MN，求折痕MN的长。‎ ‎12、如图，一副三角板拼在一起，O为AD的中点，AB = a．将△ABO沿BO对折于△A′BO，M为BC上一动点，则A′M的最小值为 ．‎ A B C D E F G A B C D E F G ‎45° ‎60° A′‎ B M A O D C ‎13、已知矩形纸片，。将纸片折叠，使顶点A与边CD上的点E重合。‎ ‎（1）如果折痕FG分别与AD，AB交于点F，G（如图（1），）求DE的长。‎ ‎（2）如果折痕FG分别与CD，AB交于点F，G（如图（2），），的外接圆与直线BC相切，求折痕FG的长。‎ ‎14、如图1，在平面直角坐标系中，O是坐标原点，□ABCD的顶点A的坐标为（－2，0），点D的坐标为（0，），点B在x轴的正半轴上，点E为线段AD的中点，过点E的直线l与x轴交于点F，与射线DC交于点G．‎ ‎（1）求∠DCB的度数；‎ ‎（2）当点F的坐标为（－4，0）时，求点G的坐标；‎ ‎（3）连结OE，以OE所在直线为对称轴，△OEF经轴对称变换后得到△OEF′ ，记直线EF′ 与射线DC的交点为H．‎ ‎①如图2，当点G在点H的左侧时，求证：△DEG∽△DHE；‎ ‎②若△EHG的面积为，请直接写出点F的坐标．‎ ‎（备用图）‎ D B O A C x E y ‎（图2）‎ D B O A G F C x l E y H F′‎ ‎（图1）‎ D B O A G F C x l E y ‎15、如图，在一面积为1的正方形纸片ABCD中，M，N分别是AD、BC边的中点，将C点折叠至MN上，落在P点的位置，折痕为BQ，连结PQ，（1）则MP=_________;（2）则PQ=__________。‎ ‎ ‎ ‎16、如图，一张长方形的纸片ABCD，其长AD为a,宽为b(a>b)在BC边上选取一点M，将⊿ABM沿AM翻折后B至B1的位置，若B1为长方形纸片ABCD的对称中心，则的值是_________。‎ ‎17、如图，在平行四边形 ABCD中，点E在边AD上，以BE为折痕，将⊿ABE向上翻折，点A正好落在CD上的点F，若⊿FDE的周长为8，⊿FCB的周长为22，则FC的长为_________。‎ ‎18、正方形纸片ABCD，E为AD的中点，将正方形纸片折起，使C点与E点重合，折痕为HF，若正方形的边长为8，那么FC=_________。折痕HF=_________。‎ ‎19、如图，已知ABCD是一矩形纸片，有是AB上一点，且BE：EA=5：3，EC=15，把⊿BCE沿折痕EC向上翻折，若点B恰好落在AD上，设这个点为F，‎ ‎（1）AB=________。（2）BC=_________。‎ ‎（3）若⊙O内切于以F、E、B、C为顶点的四边形则⊙O的面积为=________。‎ ‎20、如图，矩形ABCD沿DF折叠后，点C落在AB边上的点E处，DE、DF三等分∠ADC，若AB=6，则梯形ABFD的中位线的长为_______________.‎ ‎21、已知如图，矩形OABC的长OA=，宽OC=1，将△AOC沿AC翻折得△APC。‎ ‎（1）填空：∠PCB=____度，P点坐标为（ ， ）；‎ ‎（2）若P，A两点在抛物线y=－x2+bx+c上，求b，c的值，并说明点C在此抛物线上；‎ ‎（3）在（2）中的抛物线CP段（不包括C，P点）上，是否存在一点M，使得四边形MCAP的面积最大？若存在，求出这个最大值及此时M点的坐标；若不存在，请说明理由。‎ ‎22、如图所示，在完全重合放置的两张矩形纸片ABCD中，AB=4,BC=8,将上面的矩形纸片折叠，使点C与点A重合，折痕为EF，点D的对应点为G，连接DG,,则图中阴影部分的面积为（ ） ‎ A. B. 6 C. D. ‎ ‎23、如图，正方形纸片ABCD的边长为8，将其沿EF折叠，则图中①②③④四个三角形的周长之和为 ．‎ ‎24、如图①，将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上)，使点B落在AD边上的点 M处，点C落在点N处，MN与CD交于点P， 连接EP．‎ ‎ (1)如图②，若M为AD边的中点，‎ ‎ ①,△AEM的周长=_____cm； ②求证：EP=AE+DP；‎ ‎ (2)随着落点M在AD边上取遍所有的位置(点M不与A、D重合)，△PDM的周长是否发生变化?请说明理由．‎ 参考答案（部分）‎ ‎15、（1）． 2分 ‎（2）①；②． 6分 ‎③画图，如图所示． 8分 解：方法一：设与交于点．‎ ‎0(A)‎ B C D E ‎6‎ ‎12‎ ‎18‎ ‎24‎ x y ‎6‎ ‎12‎ ‎18‎ F M G P 在中，，‎ ‎．‎ ‎，， ‎ ‎．‎ 又，‎ ‎．‎ ‎．‎ ‎．‎ ‎． 11分 方法二：过点作，垂足为，则四边形是矩形．‎ ‎，．‎ 设，则．‎ 在中，．‎ ‎．‎ ‎．‎ ‎．‎ ‎． 11分 ‎（3）这些点形成的图象是一段抛物线． 12分 函数关系式：． 14分 说明：若考生的解答：图象是抛物线，函数关系式：均不扣分．‎ ‎22、解：（1）30，（，）；‎ ‎（2）∵点P（，），A（，0）在抛物线上 ‎∴‎ ‎∴‎ ‎∴抛物线的解析式为y=-x2+x+1‎ C点坐标为（0，1）‎ ‎∵-×02+×0+1=1 ‎ ‎∴C点在此抛物线上。‎ ‎（3）假设存在这样的点M，使得四边形MCAP的面积最大 ‎∵△ACP面积为定值， ‎ ‎∴要使四边形MCAP的面积最大，只需使△PCM的面积最大 过点M作MF⊥x轴分别交CP、CB和x轴于E、N和F，过点P作PG⊥x轴交CB于G ‎=ME·CG=ME 设M（x0，y0），‎ ‎∵∠ECN=30°，CN=x0，∴EN=x0‎ ‎∴ME=MF-EF=-x02+x0 ‎ ‎∴=-x02+x ‎∵a=-＜0，∴S有最大值 当x0=时，S的最大值是 ‎∵‎ ‎∴四边形MCAP的面积的最大值为 此时M点的坐标为（，）‎ 所以存在这样的点M（，），使得四边形MCAP的面积最大，其最大值为。‎ ‎23、y x O ‎（第21题图）‎ C1‎ O1‎ D C E B A F 解：（1）过作轴于点，如图 在中，，‎ ‎ 1分 由对称性可知：‎ ‎ 2分 点的坐标为 3分 ‎（2）设经过的抛物线的解析式为，则 ‎ 4分 解之得 抛物线的解析式为： 5分 ‎（3）与两坐标轴相切 圆心应在第一、三象限或第二、四象限的角平分线上．‎ 即在直线或上 6分 若点在直线上，根据题意有 解之得 ‎，‎ ‎ 7分 若点在直线上，根据题意有 解之得，‎ 的半径为或． 8分 ‎24、‎ ‎25、解：（1） 3分 ‎（2）如图24－2，由轴对称性质知：， 4分 A B C N M P 图 又，， 5分 ‎ 6分 点是中点，即当时，点恰好落在边上． 7分 ‎（3）i）以下分两种情况讨论：‎ ‎①当时，易见 8分 ‎②当时，如图24－3，设，分别交于，‎ A B C N M P 图 由（2）知 由题意知 ‎ ‎ （此步无写不扣分）10分 ii）当时， 易知 11分 又当时，‎ 当时（符合）， 12分 综上所述，当时，重叠部分的面积最大，其值为． 13分 ‎26、（1）过点C作CH⊥轴，垂足为H ‎ ∵在Rt△OAB中，∠OAB＝900，∠BOA＝300，AB＝2‎ ‎ ∴OB＝4，OA＝‎ ‎ 由折叠知，∠COB＝300，OC＝OA＝‎ ‎ ∴∠COH＝600，OH＝，CH＝3‎ ‎ ∴C点坐标为（，3）‎ ‎ （2）∵抛物线（≠0）经过C（，3）、A（，0）两点 ‎ ∴ 解得：‎ ‎ ∴此抛物线的解析式为：‎ ‎ （3）存在。因为的顶点坐标为（，3）即为点C ‎ MP⊥轴，设垂足为N，PN＝，因为∠BOA＝300，所以ON＝‎ ‎ ∴P（，）‎ ‎ 作PQ⊥CD，垂足为Q，ME⊥CD，垂足为E 把代入得：‎ ‎ ∴ M（，），E（，）‎ ‎ 同理：Q（，），D（，1）‎ ‎ 要使四边形CDPM为等腰梯形，只需CE＝QD ‎ 即，解得：，（舍）‎ ‎ ∴ P点坐标为（，）‎ ‎ ∴ 存在满足条件的点P，使得四边形CDPM为等腰梯形，此时P点的坐为（，）‎ ‎27、（1）选命题①‎ 证明：在图1中，∵ ∠BON = 60°， ∴ ∠CBM +∠BCN = 60°‎ ‎∵ ∠BCN +∠ACN = 60°， ∴ ∠CBM =∠ACN. ‎ 又∵ BC = CA， ∠BCM =∠CAN = 60°， ‎ ‎∴ △BCM ≌ △CAN. ‎ ‎∴ BM = CN. ‎ 选命题②‎ 证明：在图2中，∵ ∠BON = 90°， ∴ ∠CBM +∠BCN = 90°.‎ ‎∵ ∠BCN +∠DCN = 90°， ∴ ∠CBM =∠DCN. ‎ 又∵ BC = CD， ∠BCM =∠CDN = 90°，‎ ‎∴ △BCM ≌ △CDN. ‎ ‎∴ BM = CN. ‎ 选命题③‎ 证明：在图3中，∵ ∠BON = 108°， ∴ ∠CBM +∠BCN = 108°‎ ‎∵ ∠BCN +∠DCN = 108°， ∴ ∠CBM =∠DCN. ‎ 又∵ BC = CD， ∠BCM =∠CDN = 108°，‎ ‎∴ △BCM ≌ △CDN. ‎ ‎∴ BM = CN. ‎ ‎ （2）① 当∠BON = 时，结论BM = CN成立. ‎ ‎② BM = CN成立.‎ 证明：如图5，连结BD．CE.‎ 在△BCD和△CDE中，‎ ‎∵ BC = CD，∠BCD =∠CDE = 108°，CD = DE，‎ ‎∴ △BCD ≌ △CDE.‎ ‎∴ BD = CE，∠BDC =∠CED，∠DBC =∠ECD. ‎ ‎∵ ∠OBC +∠OCB = 108°，∠OCB +∠OCD = 108°，‎ ‎∴ ∠MBC =∠NCD.‎ 又∵ ∠DBC =∠ECD = 36°，∴ ∠DBM =∠ECN. ‎ ‎∴ △BDM ≌ △ECN. ‎ ‎30、解：（1）① 6 ． …………………………………………………………………………2分 ‎②（图略）取EP中点G，连接MG．梯形AEPD中，‎ ‎∵M、G分别是AD、EP的中点，‎ ‎（第30题）‎ ‎∴．……………………………………3分 由折叠得∠EMP=∠B=，又G为EP的中点，‎ ‎∴．……………………………………………4分 故．…………………………………………5分 ‎（2）△PDM的周长保持不变．‎ 证明：如图，设cm，‎ Rt△EAM中，由，‎ 可得：．…6分 ‎∵∠AME+∠AEM=，∠AME+∠PMD=，‎ ‎∴∠AEM=∠PMD．‎ 又∵∠A=∠D=，‎ ‎∴△AEM∽△DMP． ……………………………………………7分 ‎∴，即，‎ ‎∴cm．…………8分 故△PDM的周长保持不变．‎