日照市2010年中考数学试题及答案 15页

试卷类型:A ‎ 二0一0年初中学业考试 ‎ 数 学 试 题 ‎ 注意事项： ‎ ‎1．本试题分第Ⅰ卷和第Ⅱ卷两部分．第Ⅰ卷2页为选择题，36分；第Ⅱ卷8页为非选择题，84分；全卷共10页，满分120分，考试时间为120分钟．‎ ‎2．答第Ⅰ卷前，考生务必将自己的姓名、考号、考试科目涂写在答题卡上，考试结束，试题和答题卡一并收回． ‎ ‎3．第Ⅰ卷每题选出答案后，必须用2B铅笔把答题卡上对应题目的答案标号【ABCD】涂黑．如需改动，先用橡皮擦干净，再改涂其它答案． ‎ 第Ⅰ卷（选择题 共36分） ‎ 一、选择题：本大题共12小题，在每小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来．每小题选对得3分，选错、不选或选出的答案超过一个均记零分． ‎ ‎1．－3的相反数是 ‎（A）3 （B） （C） （D）－‎ ‎2．在平面直角坐标系内，把点P（－2，1）向右平移一个单位，则得到的对应点P′的坐标是 ‎（A） （－2，2） （B）（－1，1） （C）（－3，1） （D）（－2，0）‎ ‎3．已知两圆的半径分别为3cm，5 cm，且其圆心距为7cm，则这两圆的位置关系是 ‎（A）外切 （B）内切 （C）相交 （D）相离 ‎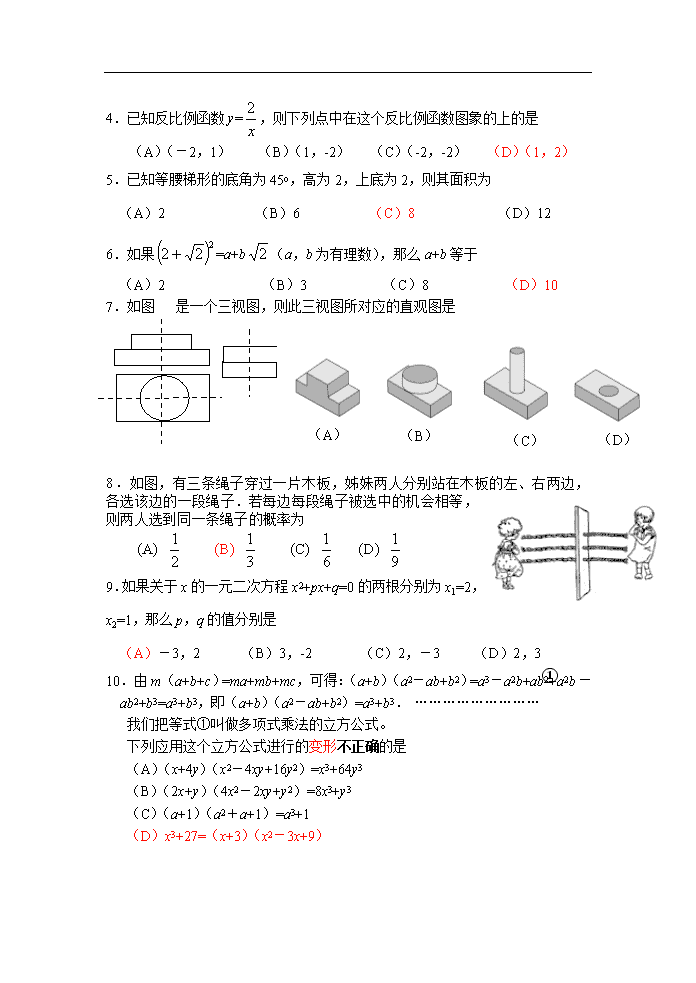4．已知反比例函数y=，则下列点中在这个反比例函数图象的上的是 ‎（A）（－2，1） （B）（1，-2） （C）（-2，-2） （D）（1，2）‎ ‎5．已知等腰梯形的底角为45o，高为2，上底为2，则其面积为 ‎（A）2 （B）6 （C）8 （D）12‎ ‎6．如果=a+b（a，b为有理数），那么a+b等于 ‎ （A）2 （B）3 （C）8 （D）10‎ ‎7．如图 是一个三视图，则此三视图所对应的直观图是 ‎（A）‎ ‎（B）‎ ‎（C）‎ ‎（D）‎ ‎8．如图，有三条绳子穿过一片木板，姊妹两人分别站在木板的左、右两边，各选该边的一段绳子．若每边每段绳子被选中的机会相等，则两人选到同一条绳子的概率为 ‎(A) (B) (C) (D) ‎ ‎9．如果关于x的一元二次方程x2+px+q=0的两根分别为x1=2，x2=1，那么p，q的值分别是 ‎（A）－3，2 （B）3，-2 （C）2，－3 （D）2，3 ‎ ‎10．由m（a+b+c）=ma+mb+mc，可得：（a+b）（a2－ab+b2）=a3－a2b+ab2+a2b－ab2+b3=a3+b3，即（a+b）（a2－ab+b2）=a3+b3． ………………………①‎ 我们把等式①叫做多项式乘法的立方公式。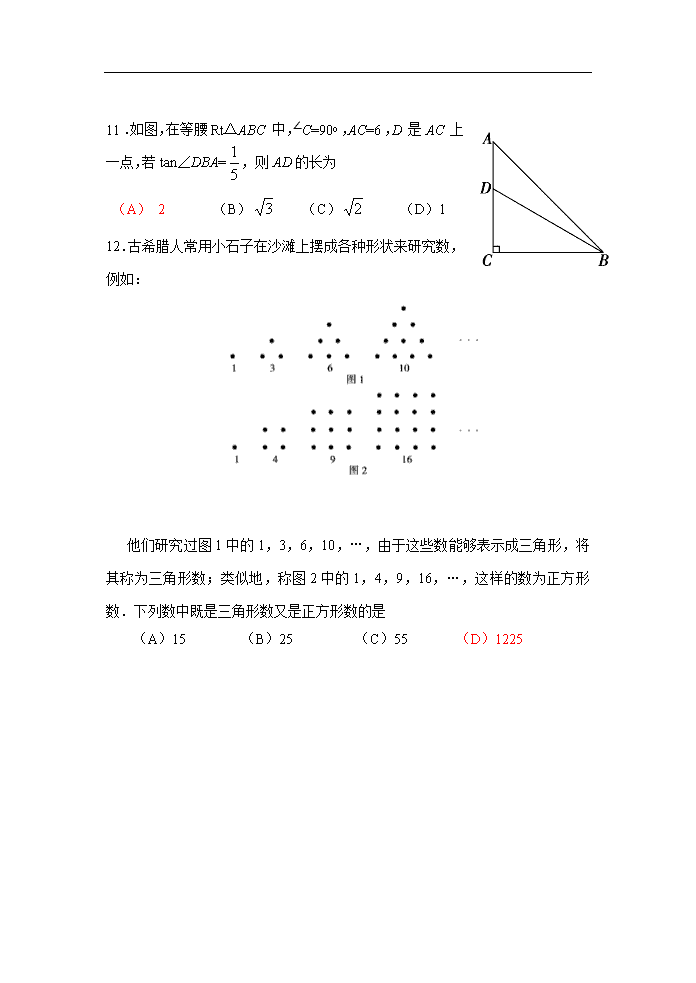‎ 下列应用这个立方公式进行的变形不正确的是 ‎（A）（x+4y）（x2－4xy+16y2）=x3+64y3‎ ‎（B）（2x+y）（4x2－2xy+y2）=8x3+y3‎ ‎（C）（a+1）（a2＋a+1）=a3+1‎ ‎（D）x3+27=（x+3）（x2－3x+9）‎ ‎11．如图，在等腰Rt△ABC中，∠C=90o，AC=6，D是AC上一点，若tan∠DBA=，则AD的长为 ‎（A） 2 （B） （C） （D）1 ‎ ‎12．古希腊人常用小石子在沙滩上摆成各种形状来研究数，例如： ‎ 他们研究过图1中的1，3，6，10，…，由于这些数能够表示成三角形，将其称为三角形数；类似地，称图2中的1，4，9，16，…，这样的数为正方形数．下列数中既是三角形数又是正方形数的是 ‎（A）15 （B）25 （C）55 （D）1225‎ ‎ ‎ ‎ 试卷类型:A ‎ 年中等学校招生考试 数 学 试 题 ‎ 第Ⅱ卷（非选择题 共84分）‎ 注意事项：‎ ‎　1．第Ⅱ卷共8页，用钢笔或圆珠笔直接写在试卷上．‎ ‎2．答卷前将密封线内的项目填写清楚．‎ 题号 二 三 总分 ‎18‎ ‎19‎ ‎20‎ ‎21‎ ‎22‎ ‎23‎ ‎24‎ 得分 二、填空题：本大题共5小题，共20分，只要求填写最后结果，每小题填对得4分．‎ ‎13．已知以下四个汽车标志图案：‎ 其中是轴对称图形的图案是 （只需填入图案代号）． ‎ ‎14．上海世博会已于2010年5月1日举行，这是继北京奥运会之后我国举办的又一世界盛事，主办机构预计这届世博会将吸引世界各地约69 500‎ ‎ 000人次参观．将69 500 000用科学记数法表示为 ．‎ ‎15．如图，C岛在A岛的北偏东50o方向，C岛在B岛的北偏西40o方向，则从C岛看A，B两岛的视角∠ACB等于 ． ‎ ‎16．如图，是二次函数y=ax2+bx+c图象的一部分，其对称轴为直线x=1，若其与x轴一交点为A（3，0），则由图象可知，不等式ax2+bx+c＜0的解集是 .‎ ‎17．一次函数y=x+4分别交x轴、y轴于A、B两点，在x轴上取一点，使△ABC为等腰三角形，则这样的的点C最多有 个． ‎ 三、解答题：本大题共7小题，共64分．解答要写出必要的文字说明、证明过程或演算步骤． ‎ 得 分 评 卷 人 ‎18．(本题满分8分) ‎ ‎ ‎ （1） 计算：；‎ ‎（2）化简，求值：，其中x=-1．‎ 得 分 评 卷 人 ‎19．(本题满分8分)‎ 我们知道不等式的两边加（或减）同一个数（或式子）不等号的方向不变．不等式组是否也具有类似的性质？完成下列填空：‎ 已知 用“<”或“>”填空 ‎5+2 3+1‎ ‎-3-1 -5-2‎ ‎1-2 4+1‎ ‎ ‎ 一般地，如果 那么a+c b+d．（用“>”或“<”填空）‎ 你能应用不等式的性质证明上述关系式吗？‎ 得 分 评 卷 人 ‎ ‎ ‎20．(本题满分9分) ‎ ‎（1）解方程组 ‎ ‎（2）列方程解应用题：‎ ‎2010年春季我国西南五省持续干旱，旱情牵动着全国人民的心。“一方有难、八方支援”，某厂计划生产1800吨纯净水支援灾区人民，为尽快把纯净水发往灾区，工人把每天的工作效率提高到原计划的1.5倍，结果比原计划提前3天完成了生产任务．求原计划每天生产多少吨纯净水？‎ 得 分 评 卷 人 ‎21．(本题满分9分)‎ 如图，四边形ABCD是边长为a的正方形，点G，E分别是边AB，BC的中点，∠AEF=90o，且EF交正方形外角的平分线CF于点F．‎ ‎ （1）证明：∠BAE=∠FEC；‎ ‎（2）证明：△AGE≌△ECF；‎ ‎（3）求△AEF的面积．‎ 得 分 评 卷 人 ‎22．(本题满分10分)‎ 为增强学生的身体素质，教育行政部门规定学生每天参加户外活动的平均时间不少于1小时。为了解学生参加户外活动的情况，对部分学生参加户外活动的时间进行抽样调查，并将调查结果绘制作成如下两幅不完整的统计图，请你根据图中提供的信息解答下列问题：‎ ‎（1）在这次调查中共调查了多少名学生？‎ ‎（2）求户外活动时间为1.5小时的人数，并补充频数分布直方图；‎ ‎（3）求表示户外活动时间 1小时的扇形圆心角的度数；‎ ‎（4）本次调查中学生参加户外活动的平均时间是否符合要求？户外活动时间的众数和中位数是多少。‎ ‎ ‎ 得 分 评 卷 人 ‎23．(本题满分10分) ‎ 如图，小明在一次高尔夫球争霸赛中，从山坡下O点打出一球向球洞A点飞去，球的飞行路线为抛物线，如果不考虑空气阻力，当球达到最大水平高度12米时，球移动的水平距离为9米 ．已知山坡OA与水平方向OC的夹角为30o，O、A两点相距8米．‎ ‎（1）求出点A的坐标及直线OA的解析式；‎ ‎（2）求出球的飞行路线所在抛物线的解析式；‎ ‎（3）判断小明这一杆能否把高尔夫球从O点直接打入球洞A点 ．‎ 得 分 评 卷 人 ‎24．(本题满分10分)‎ 如图，在△ABC中，AB=AC，以AB为直径的⊙O交AC与E，交BC与D．求证：‎ ‎（1）D是BC的中点； ‎ ‎（2）△BEC∽△ADC；‎ ‎（3）BC2=2AB·CE．‎ 二０一０年初中学业考试 数学试题参考答案及评分标准 评卷说明：‎ ‎1．选择题和填空题中的每小题，只有满分和零分两个评分档，不给中间分．‎ ‎2．解答题每小题的解答中所对应的分数，是指考生正确解答到该步骤所应得的累计分数．本答案对每小题只给出一种，对考生的其他解法，请参照评分意见进行评分．‎ ‎3．如果考生在解答的中间过程出现计算错误，但并没有改变试题的实质和难度，其后续部分酌情给分，但最多不超过正确解答分数的一半；若出现严重的逻辑错误，后续部分就不再给分．‎ 一、选择题：(本大题共12小题，每小题3分，共36分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 A B C D C D B B A C A D 二、填空题：(本大题共5小题，每小题4分，共20分)‎ ‎13．①，③ ； 14．6.95×107 ； 15．90o ；16．－1＜x＜3 ; 17．4 ． ‎ 三、解答题：(本大题共7小题, 共64分)‎ ‎18．(本小题满分8分) ‎ ‎ 解：（1）原式=4－－4+2=； ………………3分 ‎ （2）原式=‎ ‎ = ……………………5分 ‎ =x+1． …………………………………………7分 ‎ 当x=－1时，原式=． ……………………8分 ‎19．(本小题满分8分) ‎ 解：＞，＞，＜，＞； …………………………………………4分 证明：∵a>b，∴a+c>b+c． ………………………………………6分 又∵c>d，∴b+c>b+d，‎ ‎∴a+c>b+d． ………………………………………………8分 ‎20．(本题满分9分)‎ 解：（1）‎ ‎ 由（1）得：x=3+2y， （3） …………………1分 ‎ 把（3）代入（2）得：3（3+2y）－8y=13，‎ ‎ 化简 得：－2y=4，‎ ‎ ∴y=－2， ………………………………………………2分 ‎ 把y=－2代入（3），得x=－1，‎ ‎ ∴方程组的解为 ………………………………4分 ‎（2）设原计划每天生产x吨纯净水，则依据题意，得：‎ ‎ ……………………………………6分 整理，得：4.5x=900，‎ 解之，得：x=200， ……………………………………8分 把x代入原方程，成立，‎ ‎∴x=200是原方程的解．‎ 答：原计划每天生产200吨纯净水．……………………9分 ‎21．(本题满分9分)‎ ‎（1）证明：∵∠AEF=90o， ‎ ‎∴∠FEC+∠AEB=90o．………………………………………1分 在Rt△ABE中，∠AEB+∠BAE=90o，‎ ‎∴∠BAE=∠FEC；……………………………………………3分 ‎（2）证明：∵G，E分别是正方形ABCD的边AB，BC的中点，‎ ‎∴AG=GB=BE=EC，且∠AGE=180o－45o=135o．‎ 又∵CF是∠DCH的平分线，‎ ‎ ∠ECF=90o+45o=135o．………………………………………4分 在△AGE和△ECF中，‎ ‎ ‎ ‎ ∴△AGE≌△ECF； …………………………………………6分 ‎ （3）解：由△AGE≌△ECF，得AE=EF．‎ 又∵∠AEF=90o，‎ ‎∴△AEF是等腰直角三角形．………………………………7分 由AB=a，BE=a，知AE=a，‎ ‎∴S△AEF=a2．…………………………………………………9分 ‎22．（本题满分10分）‎ ‎ 解：（1）调查人数=10 20%=50（人）；…………2分 ‎（2）户外活动时间为1.5小时的人数=5024%=12（人）；……………3分 ‎ 补全频数分布直方图；…………4分 ‎（3）表示户外活动时间1小时的扇形圆心角的度数=360 o =144 o；‎ ‎……………6分 ‎（4）户外活动的平均时间=（小时）．‎ ‎∵1.18＞1 ，‎ ‎∴平均活动时间符合上级要求； …………………………………………8分 户外活动时间的众数和中位数均为1．…………………………………10分 ‎23．（本题满分10分）‎ ‎ 解：（1）在Rt△AOC中，‎ ‎∵∠AOC=30 o ，OA=8，‎ ‎∴AC=OA·sin30o=8×=，‎ ‎ OC=OA·cos30o=8×=12．‎ ‎∴点A的坐标为（12，）． …………………………………2分 设OA的解析式为y=kx，把点A（12，）的坐标代入得：‎ ‎ =12k ，‎ ‎∴k= ，‎ ‎∴OA的解析式为y=x； …………………… ……………………4分 ‎(2) ∵顶点B的坐标是（9，12）, 点O的坐标是（0，0）‎ ‎∴设抛物线的解析式为y=a(x-9)+12，…………………………………6分 把点O的坐标代入得：‎ ‎0=a（0-9）+12，解得a= ，‎ ‎∴抛物线的解析式为y= (x-9)+12 ‎ 及y= x+ x； …………………………………………………8分 ‎(3) ∵当x=12时，y= ，‎ ‎∴小明这一杆不能把高尔夫球从O点直接打入球洞A点． …………10分 ‎24．（本题满分10分） ‎ ‎（1）证明：∵AB是⊙O的直径，∴∠ADB=90° ，‎ 即AD是底边BC上的高． ………………………………………1分 又∵AB=AC，∴△ABC是等腰三角形， ‎ ‎∴D是BC的中点；………… ……………………………………………3分 ‎ (2) 证明：∵∠CBE与∠CAD是同弧所对的圆周角，‎ ‎ ∴ ∠CBE=∠CAD．…………………………………………………5分 ‎ 又∵ ∠BCE=∠ACD，‎ ‎ ∴△BEC∽△ADC；…………………………………………………6分 ‎（3）证明：由△BEC∽△ADC，知，‎ 即CD·BC=AC·CE． …………………………………………………8分 ‎∵D是BC的中点，∴CD=BC． ‎ ‎ 又 ∵AB=AC，∴CD·BC=AC·CE=BC ·BC=AB·CE 即BC=2AB·CE．……………………………………………………10分