全国中考数学试题分类解析汇编套专题专题反比例函数的应用 30页

‎2012年全国中考数学试题分类解析汇编(159套63专题）‎ 专题19：反比例函数的应用 一、选择题 ‎1. （2012福建福州4分）如图，过点C(1，2)分别作x轴、y轴的平行线，交直线y＝－x＋6于A、B 两点，若反比例函数y＝(x＞0)的图像与△ABC有公共点，则k的取值范围是【 】‎ ‎ A．2≤k≤9 B．2≤k≤‎8 C．2≤k≤5 D．5≤k≤8‎ ‎【答案】A。‎ ‎【考点】反比例函数综合题，曲线上点的坐标与方程的关系，二次函数的性质。‎ ‎【分析】∵ 点C(1，2)，BC∥y轴，AC∥x轴，‎ ‎∴ 当x＝1时，y＝－1＋6＝5；当y＝2时，－x＋6＝2，解得x＝4。‎ ‎∴ 点A、B的坐标分别为A(4，2)，B(1，5)。‎ 根据反比例函数系数的几何意义，当反比例函数与点C相交时，k＝1×2＝2最小。‎ 设与线段AB相交于点(x，－x＋6)时k值最大，‎ 则k＝x(－x＋6)＝－x2＋6x＝－(x－3)2＋9。‎ ‎∵ 1≤x≤4，∴ 当x＝3时，k值最大，此时交点坐标为(3，3)。‎ 因此，k的取值范围是2≤k≤9。故选A。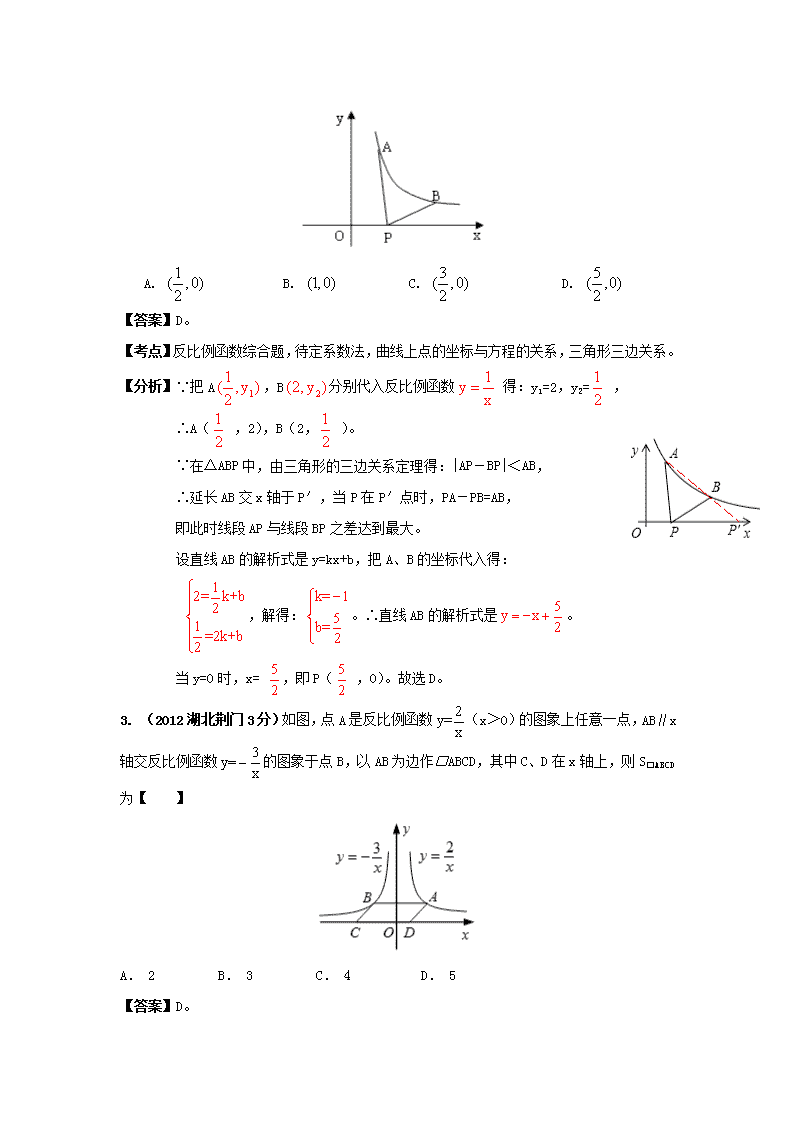‎ ‎2. （2012湖北黄石3分）如图所示，已知A，B为反比例函数图像上的两点，动 点P在x正半轴上运动，当线段AP与线段BP之差达到最大时，点P的坐标是【 】‎ A. B. C. D. ‎ ‎【答案】D。‎ ‎【考点】反比例函数综合题，待定系数法，曲线上点的坐标与方程的关系，三角形三边关系。‎ ‎【分析】∵把A，B分别代入反比例函数 得：y1=2，y2= ，‎ ‎∴A（ ，2），B（2， ）。‎ ‎∵在△ABP中，由三角形的三边关系定理得：|AP－BP|＜AB，‎ ‎∴延长AB交x轴于P′，当P在P′点时，PA－PB=AB，‎ 即此时线段AP与线段BP之差达到最大。‎ 设直线AB的解析式是y=kx+b，把A、B的坐标代入得：‎ ‎ ，解得：。∴直线AB的解析式是。‎ 当y=0时，x= ，即P（ ，0）。故选D。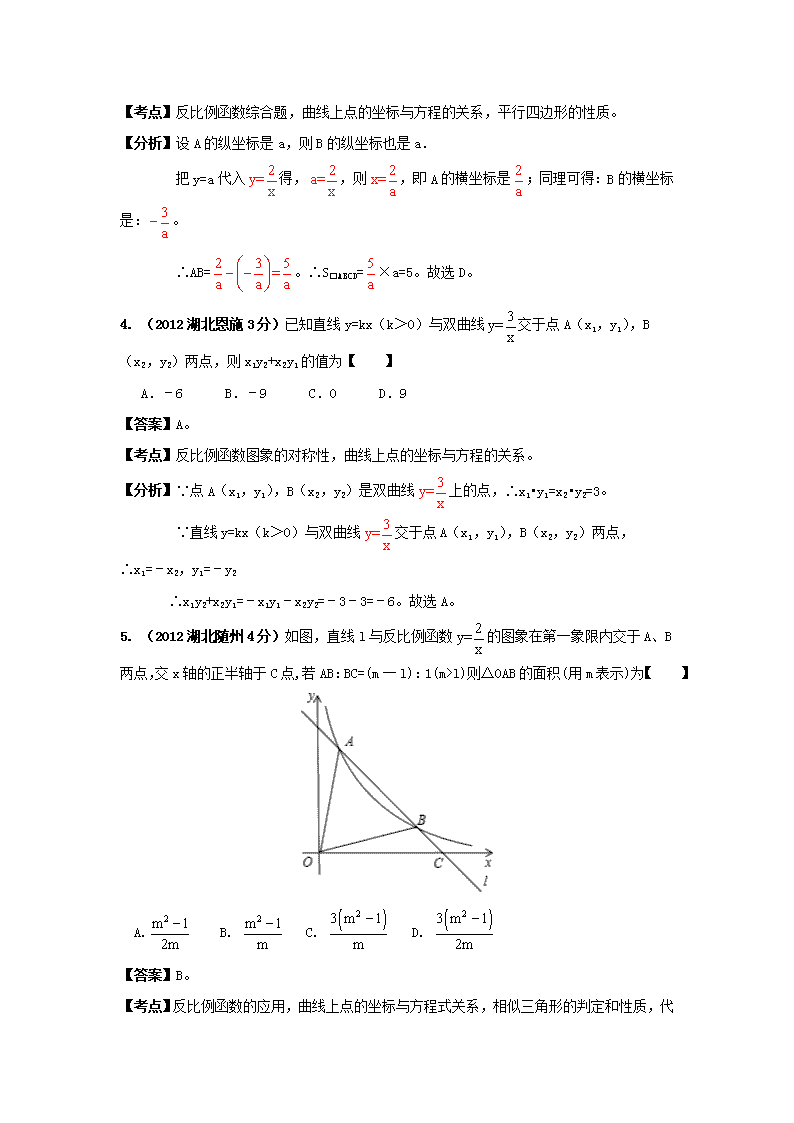‎ ‎3. （2012湖北荆门3分）如图，点A是反比例函数（x＞0）的图象上任意一点，AB∥x轴交反比例函数的图象于点B，以AB为边作□ABCD，其中C、D在x轴上，则S□ABCD为【 】‎ A． 2 B． ‎3 C． 4 D． 5‎ ‎【答案】D。‎ ‎【考点】反比例函数综合题，曲线上点的坐标与方程的关系，平行四边形的性质。‎ ‎【分析】设A的纵坐标是a，则B的纵坐标也是a．‎ 把y=a代入得，，则，即A的横坐标是；同理可得：B的横坐标是：。‎ ‎∴AB=。∴S□ABCD=×a=5。故选D。‎ ‎4. （2012湖北恩施3分）已知直线y=kx（k＞0）与双曲线交于点A（x1，y1），B（x2，y2）两点，则x1y2+x2y1的值为【 】‎ A．﹣6 B．﹣‎9 C．0 D．9‎ ‎【答案】A。‎ ‎【考点】反比例函数图象的对称性，曲线上点的坐标与方程的关系。‎ ‎【分析】∵点A（x1，y1），B（x2，y2）是双曲线上的点，∴x1•y1=x2•y2=3。‎ ‎ ∵直线y=kx（k＞0）与双曲线交于点A（x1，y1），B（x2，y2）两点，∴x1=﹣x2，y1=﹣y2‎ ‎∴x1y2+x2y1=﹣x1y1﹣x2y2=﹣3﹣3=﹣6。故选A。‎ ‎5. （2012湖北随州4分）如图，直线l与反比例函数的图象在第一象限内交于A、B两点，交x轴的正半轴于C点,若AB：BC=(m一l)：1(m>l)则△OAB的面积(用m表示)为【 】‎ ‎ A. B. C. D. ‎ ‎【答案】B。‎ ‎【考点】‎ 反比例函数的应用，曲线上点的坐标与方程式关系，相似三角形的判定和性质，代数式化简。‎ ‎【分析】如图，过点A作AD⊥OC于点D，过点B作BE⊥OC于点E,‎ ‎ 设A(ｘA，ｙA)，B (ｘB，ｙB)，C（c¸0）。‎ ‎ ∵AB：BC=(m一l)：1(m>l)，∴AC：BC=m：1。‎ ‎ 又∵△ADC∽△BEC，∴AD：BE=DC：EC= AC：BC=m：1。‎ ‎ 又∵AD=ｙA，BE=ｙB，DC= c－ｘA，EC= c－ｘB，‎ ‎ ∴ｙA：ｙB= m：1，即ｙA= mｙB。‎ ‎ ∵直线l与反比例函数的图象在第一象限内交于A、B两点， ‎ ‎ ∴，。‎ ‎ ∴，。‎ 将 又由AC：BC=m：1得（c－ｘA）：（c－ｘB）=m：1，即 ‎ ，解得。‎ ‎ ∴‎ ‎。‎ ‎ 故选B。‎ ‎6. （2012湖南株洲3分）如图，直线x=t（t＞0）与反比例函数的图象分别交于B、C两点，A为y轴上的任意一点，则△ABC的面积为【 】‎ ‎　　A．3　　B．t　　C．　　D．不能确定 ‎【答案】C。‎ ‎【考点】反比例函数系数k的几何意义，曲线上点的坐标与方程的关系。‎ ‎【分析】把x=t分别代入，得，∴B（t，）、C（t，）。‎ ‎∴BC=﹣（）=。‎ ‎∵A为y轴上的任意一点，∴点A到直线BC的距离为t。‎ ‎∴△ABC的面积=。故选C。‎ ‎7. （2012四川泸州2分）如图，矩形ABCD中，C是AB的中点，反比例函数 (k＞0)在第一象限的图象经过A、C两点，若△OAB面积为6，则k的值为【 】‎ A、2 B、‎4 ‎C、8 D、16‎ ‎【答案】B。‎ ‎【考点】反比例函数系数k的几何意义，三角形中位线定理。‎ ‎【分析】如图，分别过点A、点C作OB的垂线，垂足分别为点M、点N， ‎ ‎∵点C为AB的中点，∴CE为△AMB的中位线。‎ ‎∴MN=NB=a，CN=b，AM=2b。‎ 又∵OM•AM=ON•CN，∴OM=a。‎ ‎∴△OAB面积=‎3a•2b÷2=3ab=6。‎ ‎∴ab=2。∴k=a•2b=2ab=4。故选B。‎ ‎8. （2012辽宁丹东3分）如图，点A是双曲线在第二象限分支上的任意一点，点B、点C、点D 分别是点A关于x轴、坐标原点、y轴的对称点．若四边形ABCD的面积是8，则k的值为【 】‎ A.-1 B‎.1 C.2 D.-2‎ ‎【答案】D。‎ ‎【考点】反比例函数系数k的几何意义，关于原点对称、x轴、y轴对称的点的坐标，矩形的判定和性质。‎ ‎【分析】∵点B、点C、点D分别是点A关于x轴、坐标原点、y轴的对称点，∴四边形ABCD是矩形。∵四边形ABCD的面积是8，∴4×|－k|=8，解得|k|=2。‎ 又∵双曲线位于第二、四象限，∴k＜0。∴k=－2。故选D。‎ ‎9. （2012辽宁铁岭3分）如图，点A在双曲线上，点B在双曲线（k≠0）上，AB∥x轴，分别过点A、B向x轴作垂线，垂足分别为D、C，若矩形ABCD的面积是8，则k的值为【 】‎ A.12 B‎.10 C.8 D.6‎ ‎【答案】A。‎ ‎【考点】反比例函数系数k的几何意义，曲线上点的坐标与方程的关系，平行的性质，矩形的判定和性质。‎ ‎【分析】∵双曲线（k≠0）在第一象限，∴k＞0。‎ ‎ 延长线段BA，交y轴于点E。‎ ‎∵AB∥x轴，∴AE⊥y轴。∴四边形AEOD是矩形。‎ ‎∵点A在双曲线上，∴=4。‎ 同理 =k。‎ ‎∵， ∴k=12。故选A。‎ ‎10. （2012山东德州3分）如图，两个反比例函数和的图象分别是l1和l2．设点P在l1上，PC⊥x轴，垂足为C，交l2于点A，PD⊥y轴，垂足为D，交l2于点B，则三角形PAB的面积为【 】‎ A．3 B．‎4 C． D．5‎ ‎【答案】C。‎ ‎【考点】反比例函数综合题，曲线上点的坐标与方程的关系，三角形的面积。‎ ‎11. （2012山东临沂3分）如图，若点M是轴正半轴上任意一点，过点M作PQ∥轴，分别交函数和的图象于点P和Q，连接OP和OQ．则下列结论正确的是【 】‎ A．∠POQ不可能等于90°　　 B．　　‎ C．这两个函数的图象一定关于轴对称　 　D．△POQ的面积是 ‎【答案】D。‎ ‎【考点】反比例函数综合题，直角三角形的判定，反比例函数的性质，反比例函数系数的几何意义。‎ ‎【分析】根据反比例函数的性质逐一作出判断：‎ A．∵当PM=MO=MQ时，∠POQ=90°，故此选项错误；‎ B．根据反比例函数的性质，由图形可得：＞0，＜0，而PM，QM为线段一定为正值，故，故此选项错误；‎ C．根据，的值不确定，得出这两个函数的图象不一定关于轴对称，故此选项错误；‎ D．∵||=PM•MO，||=MQ•MO，‎ ‎∴△POQ的面积=MO•PQ=MO（PM+MQ）=MO•PM+MO•MQ=。‎ 故此选项正确。‎ 故选D。‎ ‎12. （2012山东威海3分）下列选项中，阴影部分面积最小的是【 】‎ ‎【答案】C。‎ ‎【考点】反比例函数的图象和性质。‎ ‎【分析】根据反比例函数的图象和性质，A，B，D三个图形中阴影部分面积均为2。而C图形中阴影部分面积为。故选C。‎ 二、填空题 ‎1. （2012广东深圳3分）如图，双曲线与⊙O在第一象限内交于P、Q 两点，分别过P、Q两点向x轴和y轴作垂线，已知点P坐标为(1，3)，则图中阴影部分的面积为 ▲ ．‎ ‎【答案】4。‎ ‎【考点】反比例函数综合题 ‎【分析】∵⊙O在第一象限关于y=x对称，也关于y=x对称，P点坐标是（1，3），‎ ‎ ∴Q点的坐标是（3，1），‎ ‎∴S阴影=1×3+1×3－2×1×1=4。‎ ‎2. （2012浙江衢州4分）如图，已知函数y=2x和函数的图象交于A、B两点，过点A作AE⊥x轴于点E，若△AOE的面积为4，P是坐标平面上的点，且以点B、O、E、P为顶点的四边形是平行四边形，则满足条件的P点坐标是　 ▲ 　．‎ ‎【答案】（0，﹣4），（﹣4，﹣4），（4，4）。‎ ‎【考点】反比例函数综合题，平行四边形的性质。‎ ‎【分析】先求出B、O、E的坐标，再根据平行四边形的性质画出图形，即可求出P点的坐标：‎ 如图，∵△AOE的面积为4，函数的图象过一、三象限，∴k=8。‎ ‎∴反比例函数为 ‎∵函数y=2x和函数的图象交于A、B两点，‎ ‎∴A、B两点的坐标是：（2，4）（﹣2，﹣4），‎ ‎∵以点B、O、E、P为顶点的平行四边形共有3个，‎ ‎∴满足条件的P点有3个，分别为：P1（0，﹣4），P2（﹣4，﹣4），P3（4，4）。‎ ‎3. （2012浙江温州5分）如图，已知动点A在函数(x>o)的图象上，AB⊥x轴于点B，AC⊥y轴于点C，延长CA至点D，使AD=AB，延长BA至点Ｅ，使AE=AC.直线DE分别交x轴，y轴于点P,Q.当QE：DP=4:9时，图中的阴影部分的面积等于 ▲ _.‎ ‎【答案】。‎ ‎【考点】反比例函数综合题，曲线上坐标与方程的关系，勾股定理，相似三角形的判定和性质。‎ ‎【分析】过点D作DG⊥x轴于点G，过点E作EF⊥y轴于点F。‎ ‎∵A在函数(x>o)的图象上，∴设A（t，），‎ 则AD=AB=DG= ，AE=AC=EF=t。‎ 在Rt△ADE中，由勾股定理，得 ‎。‎ ‎∵△EFQ∽△DAE，∴QE：DE=EF：AD。∴QE=。‎ ‎∵△ADE∽△GPD，∴DE：PD=AE：DG。∴DP=。‎ 又∵QE：DP=4：9，∴ 。解得。‎ ‎∴图中阴影部分的面积=。‎ ‎4. （2012江苏常州2分）如图，已知反比例函数和 ‎。点A在y轴的正半轴上，过点A作直线BC∥x轴，且分别与两个反比例函数的图象交于点B和C，连接OC、OB。若△BOC的面积为，AC：AB=2：3，则= ▲ ，= ▲ 。‎ ‎5. （2012江苏苏州3分）如图，已知第一象限内的图象是反比例函数图象的一个分支，第二象限 内的图象是反比例函数图象的一个分支，在轴上方有一条平行于轴的直线与它们分别交于点A、‎ B，过点A、B作轴的垂线，垂足分别为C、D.若四边形ACDB的周长为8且AB0）的图象上，则 ▲ ．‎ ‎【答案】。‎ ‎【考点】反比例函数综合题。‎ ‎【分析】∵⊙O1过原点O，⊙O1的半径O1P1，∴O1O=O1P1。‎ ‎∵⊙O1的半径O1P1与x轴垂直，点P1（x1，y1）在反比例函数（x＞0）的图象上，‎ ‎∴x1=y1，x1y1=1。∴x1=y1=1。‎ ‎∵⊙O1与⊙O2相外切，⊙O2的半径O2P2与x轴垂直，‎ 设两圆相切于点A，∴AO2=O2P2=y2，OO2=2+y2。‎ ‎∴P2点的坐标为：（2+y2，y2）。‎ ‎∵点P2在反比例函数（x＞0）的图象上，‎ ‎∴（2+y2）•y2=1，解得：y2=－1+ 或－1－（不合题意舍去）。‎ ‎∴y1+y2=1+（－1+）= 。‎ ‎9. （2012福建漳州4分）如图，点A(3，n)在双曲线y=上，过点A作 AC⊥x轴，垂足为C．线段OA的垂直平分线交OC于点B，则△ABC周长的值是 ▲ ．‎ ‎【答案】4。‎ ‎【考点】反比例函数的图象和性质，曲线上点的坐标与方程的关系，线段垂直平分线的性质，勾股定理。‎ ‎【分析】由点A(3，n)在双曲线y=上得，n=1。∴A(3，1)。‎ ‎ ∵线段OA的垂直平分线交OC于点B，∴OB=AB。‎ ‎ 则在△ABC中， AC=1，AB＋BC=OB＋BC=OC=3，‎ ‎ ∴△ABC周长的值是4。‎ ‎10. （2012福建三明4分）如图，点A在双曲线上，点B在双曲线上，且AB//y 轴，点P是轴上的任意一点，则△PAB的面积为 ▲ ．‎ ‎【答案】1。‎ ‎【考点】反比例函数的图象和性质，曲线上点的坐标与方程的关系。‎ ‎【分析】∵点A在双曲线上，点B在双曲线上，且AB//y轴，‎ ‎ ∴可设A（x，），B（x，）。‎ ‎ ∴AB=，AB边上的高为x。‎ ‎ ∴△PAB的面积为。‎ ‎11. （2012湖南湘潭3分）近视眼镜的度数y（度）与镜片焦距x（m）成反比例（即），已知200度近视眼镜的镜片焦距为‎0.5m，则y与x之间的函数关系式是　 ▲ ．‎ ‎【答案】。‎ ‎【考点】根据实际问题列反比例函数关系式。‎ ‎【分析】由于点（0.5，200）适合这个函数解析式，则k=0.5×200=100，∴。‎ 故眼镜度数y与镜片焦距x之间的函数关系式为：。‎ ‎12. （2012四川成都4分）‎ 如图，在平面直角坐标系xOy中，直线AB与x轴、y轴分别交于点A，B，与反比例函数 (为常数，且)在第一象限的图象交于点E，F．过点E作EM⊥y轴于M，过点F作FN⊥x轴于N，直线EM与FN交于点C．若 (为大于l的常数)．记△CEF的面积为S1，△OEF的面积为S2，则 = ▲ ． (用含的代数式表示)‎ ‎【答案】。‎ ‎【考点】反比例函数综合题，曲线上点的坐标与方程的关系，相似三角形的判定和性质。。‎ ‎【分析】过点F作FD⊥BO于点D，EW⊥AO于点W，‎ ‎∵，∴。‎ 设E点坐标为：（x，my），则F点坐标为：（mx，y），‎ ‎∴△CEF的面积为：S1=（mx﹣x）（my﹣y）=（m﹣1）2xy。‎ ‎∵△OEF的面积为：S2=S矩形CNOM﹣S1﹣S△MEO﹣S△FON ‎=MC•CN﹣（m﹣1）2xy﹣ME•MO﹣FN•NO ‎=mx•my﹣（m﹣1）2xy﹣x•my﹣y•mx=m2xy﹣（m﹣1）2xy﹣mxy ‎=（m2﹣1）xy=（m+1）（m﹣1）xy，‎ ‎∴。‎ ‎13. （2012山东聊城3分）如图，在直角坐标系中，正方形的中心在原点O，且正方形的一组对边与x轴平行，点P（‎3a，a）是反比例函数（k＞0）的图象上与正方形的一个交点．若图中阴影部分的面积等于9，则这个反比例函数的解析式为　 ▲ 　．‎ ‎【答案】。‎ ‎【考点】待定系数法，曲线上点的坐标与方程的关系，反比例函数图象的对称性，正方形的性质。‎ ‎【分析】由反比例函数的对称性可知阴影部分的面积和正好为小正方形面积的，设小正方形的边长为b，图中阴影部分的面积等于9可求出b的值，从而可得出直线AB的表达式，再根据点P（‎3a，a）在直线AB上可求出a的值，从而得出反比例函数的解析式：‎ ‎∵反比例函数的图象关于原点对称，∴阴影部分的面积和正好为小正方形的面积。‎ 设正方形的边长为b，则b2=9，解得b=6。‎ ‎∵正方形的中心在原点O，∴直线AB的解析式为：x=3。‎ ‎∵点P（‎3a，a）在直线AB上，∴‎3a=3，解得a=1。∴P（3，1）。‎ ‎∵点P在反比例函数（k＞0）的图象上，∴k=3×1=3。‎ ‎∴此反比例函数的解析式为：。‎ ‎14. （2012山东日照4分）如图，点A在双曲线上，过A作AC⊥x轴，垂足为C，OA的垂直平分线交OC于点B，当OA＝4时，则△ABC周长为 ▲ . ‎ ‎【答案】。‎ ‎【考点】反比例函数综合题，曲线上点的坐标与方程的关系，勾股定理，线段垂直平分线的性质。‎ ‎【分析】根据线段垂直平分线的性质可知AB=OB，由此推出△ABC的周长=OC+AC，设OC=a，AC=b，根据勾股定理和函数解析式即可得到关于a、b的方程组，解之即可求出△ABC的周长。‎ 设A（a，b），则OC=a，AC=b。‎ ‎∵点A在双曲线上，∴ ，即ab=6。‎ ‎∵OA=4，∴a2＋b2=42，即（a＋b）2－2ab=16，即（a＋b）2－2×6=16，∴a＋b=。‎ ‎∵OA的垂直平分线交OC于B，∴AB=OB。‎ ‎∴△ABC的周长=OC+AC= a＋b=。‎ ‎15. （2012河南省5分）如图，点A，B在反比例函数的图像上，过点A，B作x轴的垂线，垂足分别为M，N，延长线段AB交x轴于点C，若OM=MN=NC，△AOC的面积为6，则k值为 ▲ ‎ ‎【答案】4。‎ ‎【考点】反比例函数综合题。‎ ‎【分析】设OM=a，‎ ‎∵点A在反比例函数上，∴AM=。‎ ‎∵OM=MN=NC，∴OC=‎3a。‎ ‎∴S△AOC=•OC•AM=×‎3a×=k=6。解得k=4。‎ ‎16. （2012甘肃兰州4分）如图，点A在双曲线上，点B在双曲线上，且AB∥x轴，C、D在x轴上，若四边形ABCD为矩形，则它的面积为　 ▲ 　．‎ ‎【答案】2。‎ ‎【考点】反比例函数系数k的几何意义。‎ ‎【分析】如图，过A点作AE⊥y轴，垂足为E，‎ ‎∵点A在双曲线上，∴四边形AEOD的面积为1。‎ ‎∵点B在双曲线上，且AB∥x轴，∴四边形BEOC的面积为3。‎ ‎∴四边形ABCD为矩形，则它的面积为3－1＝2。‎ 三、解答题 ‎1. （2012重庆市10分）已知：如图，在平面直角坐标系中，一次函数y=ax+b（a≠0）的图象与反比例函数的图象交于一、三象限内的A．B两点，与x轴交于C点，点A的坐标为（2，m)，点B的坐标为（n，－2），tan∠BOC＝。‎ ‎（l）求该反比例函数和一次函数的解析式；‎ ‎（2）在x轴上有一点E（O点除外），使得△BCE与△BCO的面积相等，求出点E的坐标．‎ ‎【答案】解：（1）过B点作BD⊥x轴，垂足为D，‎ ‎∵B（n，－2），∴BD=2。‎ 在Rt△OBD中，tan∠BOC= ，即 ，‎ 解得OD=5。‎ 又∵B点在第三象限，∴B（－5，－2）。‎ 将B（－5，－2）代入 中，得k=xy=10。‎ ‎∴反比例函数解析式为。‎ 将A（2，m）代入中，得m=5，∴A（2，5），‎ 将A（2，5），B（－5，－2）代入y=ax+b中，‎ 得，解得。‎ ‎∴一次函数解析式为y=x+3。 （2）由y=x+3得C（－3，0），即OC=3。‎ ‎∵S△BCE=S△BCO，∴CE=OC=3，∴OE=6，即E（－6，0）。‎ ‎【考点】反比例函数综合题，曲线上点的坐标与方程的关系，锐角三角函数定义。‎ ‎【分析】（1）过B点作BD⊥x轴，垂足为D，由B（n，－2）得BD=2，由tan∠BOC=，解直角三角形求OD，确定B点坐标，得出反比例函数关系式。再由A、B两点横坐标与纵坐标的积相等求n的值，由“两点法”求直线AB的解析式。‎ ‎（2）点E为x轴上的点，要使得△BCE与△BCO的面积相等，只需要CE=CO即可，根据直线AB解析式求CO，再确定E点坐标。‎ ‎2. （2012安徽省12分）甲、乙两家商场进行促销活动，甲商场采用“慢200减‎100”‎的促销方式，即购买商品的总金额满200元但不足400元，少付100元；满400元但不足600元，少付200元；……，乙商场按顾客购买商品的总金额打6折促销。‎ ‎（1）若顾客在甲商场购买了510元的商品，付款时应付多少钱？‎ ‎（2）若顾客在甲商场购买商品的总金额为x（400≤x＜600）元，优惠后得到商家的优惠率为p（p=），写出p与x之间的函数关系式，并说明p随x的变化情况；‎ ‎（3）品牌、质量、规格等都相同的某种商品，在甲乙两商场的标价都是x（200≤x＜400）元，你认为选择哪家商场购买商品花钱较少？请说明理由。‎ ‎【答案】解：（1）顾客在甲商场购买了510元的商品，付款时应付510－200=310（元）。‎ ‎（2）p与x之间的函数关系式为。‎ ‎∵200＞0，∴p随x的增大而减小。‎ ‎（3）购x元（200≤x＜400）在甲商场的优惠额是100元，乙商场的优惠额是x－0.6x=0.4x。‎ 当0.4x＜100，即200≤x＜250时，选甲商场购买商品花钱较少；‎ 当0.4x=100，即x=250时，选甲乙商场一样优惠；‎ 当0.4x＞100，即250＜x＜4000时，选乙商场购买商品花钱较少。‎ ‎【考点】反比例函数的性质和应用。‎ ‎【分析】（1）根据题意直接列出算式510-200即可。‎ ‎（2）根据商家的优惠率即可列出p与x之间的函数关系式，并能得出p随x的变化情况。‎ ‎（3）先设购买商品的总金额为x元，（200≤x＜400），得出甲商场需花x-100元，乙商场需花0.6x元，然后分三种情况列出不等式和方程即可。‎ ‎3. （2012浙江丽水、金华8分）如图，等边△OAB和等边△AFE的一边都在x轴上，双曲线y＝(k＞0)经过边OB的中点C和AE的中点D．已知等边△OAB的边长为4．‎ ‎(1)求该双曲线所表示的函数解析式；‎ ‎(2)求等边△AEF的边长．‎ ‎【答案】解：(1)　过点C作CG⊥OA于点G，‎ ‎∵点C是等边△OAB的边OB的中点，‎ ‎∴OC＝2，∠ AOB＝60°。∴OG＝1，CG＝，‎ ‎∴点C的坐标是(1，)。由，得：k＝。‎ ‎∴该双曲线所表示的函数解析式为。‎ ‎(2)　过点D作DH⊥AF于点H，设AH＝a，则DH＝a。‎ ‎∴点D的坐标为(4＋a，a)。‎ ‎∵点D是双曲线上的点，‎ ‎∴由xy＝，得a (4＋a)＝，即：a2＋‎4a－1＝0。‎ 解得：a1＝－2，a2＝－－2(舍去)。∴AD＝2AH＝2－4。‎ ‎∴等边△AEF的边长是2AD＝4－8。．‎ ‎【考点】反比例函数综合题，等边三角形的性质，曲线上点的坐标与方程的关系，解一元二次方程。‎ ‎【分析】(1)过点C作CG⊥OA于点G，根据等边三角形的性质求出OG、CG的长度，从而得到点C的坐标，再利用待定系数法求反比例函数解析式列式计算即可得解。‎ ‎(2)过点D作DH⊥AF于点H，设AH＝a，根据等边三角形的性质表示出DH的长度，然后表示出点D的坐标，再把点D的坐标代入反比例函数解析式，解方程得到a的值，从而得解。‎ ‎4. （2012浙江义乌8分）如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为对角线OB的中点，点E（4，n）在边AB上，反比例函数（k≠0）在第一象限内的图象经过点D、E，且tan∠BOA=．‎ ‎（1）求边AB的长；‎ ‎（2）求反比例函数的解析式和n的值；‎ ‎（3）若反比例函数的图象与矩形的边BC交于点F，将矩形折叠，使点O与点F重合，折痕分别与x、y轴正半轴交于点H、G，求线段OG的长．‎ ‎【答案】解：（1）∵点E（4，n）在边AB上，∴OA=4，‎ ‎ 在Rt△AOB中，∵tan∠BOA=，∴AB=OA×tan∠BOA=4×=2。‎ ‎（2）由（1），可得点B的坐标为（4，2），‎ ‎∵点D为OB的中点，∴点D（2，1）。‎ ‎∵点D在反比例函数（k≠0）的图象上，∴，解得k=2。‎ ‎∴反比例函数解析式为。‎ 又∵点E（4，n）在反比例函数图象上，∴。‎ ‎（3）如图，设点F（a，2），‎ ‎∵反比例函数的图象与矩形的边BC交于点F，‎ ‎∴，解得a=1。∴CF=1。‎ 连接FG，设OG=t，则OG=FG=t，CG=2﹣t，‎ 在Rt△CGF中，GF2=CF2+CG2，即t2=（2﹣t）2+12，‎ 解得t=，∴OG=t=。‎ ‎【考点】反比例函数综合题，锐角三角函数定义，曲线上点的坐标与方程的关系，折叠对称的性质，勾股定理。‎ ‎【分析】（1）由点E的纵坐标得出OA=4，再根据tan∠BOA= 即可求出AB的长度；‎ ‎（2）根据（1）求出点B的坐标，再根据点D是OB的中点求出点D的坐标，然后利用待定系数法求函数解析式求出反比例函数解析式，再把点E的坐标代入进行计算即可求出n的值。‎ ‎（3）利用反比例函数解析式求出点F的坐标，从而得到CF的长度，连接FG，根据折叠的性质可得FG=OG，然后用OG表示出CG的长度，再利用勾股定理列式计算即可求出OG的长度。‎ ‎5. （2012四川攀枝花8分）据媒体报道，近期“手足口病”可能进入发病高峰期，某校根据《学校卫生工作条例》，为预防“手足口病”，对教室进行“薰药消毒”．已知药物在燃烧机释放过程中，室内空气中每立方米含药量y（毫克）与燃烧时间x（分钟）之间的关系如图所示（即图中线段OA和双曲线在A点及其右侧的部分），根据图象所示信息，解答下列问题：‎ ‎（1）写出从药物释放开始，y与x之间的函数关系式及自变量的取值范围；‎ ‎（2）据测定，当空气中每立方米的含药量低于2毫克时，对人体无毒害作用，那么从消毒开始，至少在多长时间内，师生不能进入教室？‎ ‎【答案】解：（1）设反比例函数解析式为，将（25，6）代入解析式得，k=25×6=150，‎ ‎∴函数解析式为（x＞15）。‎ 将y=10代入解析式得，，解得x=15。∴A（15，10）。‎ 设正比例函数解析式为y=nx，‎ 将A（15，10）代入上式，得。‎ ‎∴正比例函数解析式为y=x（0≤x≤15）。‎ 综上所述，从药物释放开始，y与x之间的函数关系式为。‎ ‎（2）由解得x=75（分钟），‎ ‎ ∵消毒开始的时间是在15分钟时，∴75－15=60（分钟）。‎ 答：从消毒开始，至少在60分钟内，师生不能进入教室。‎ ‎【考点】反比例函数的应用，待定系数法，曲线上点的坐标与方程的关系。‎ ‎【分析】（1）首先根据题意，用待定系数法将数据（25，6）代入求得反比例函数的关系式，从而得到点A 的坐标；用待定系数法将点A 的坐标代入求得正比例函数的关系式。根据点A 的坐标确定自变量的取值范围。‎ ‎ （2）因为是从消毒开始，所以将y=2代入求出x的值，再用它减去消毒开始的时间即可得到从消毒开始，至少在60分钟内，师生不能进入教室的结论。‎ ‎6. （2012山东济南9分）如图，已知双曲线，经过点D（6，1），点C是双曲线第三象限上的动点，过C作CA⊥x轴，过D作DB⊥y轴，垂足分别为A，B，连接AB，BC．‎ ‎（1）求k的值；‎ ‎（2）若△BCD的面积为12，求直线CD的解析式；‎ ‎（3）判断AB与CD的位置关系，并说明理由．‎ ‎【答案】解：（1）∵双曲线经过点D（6，1），∴，解得k=6。‎ ‎（2）设点C到BD的距离为h，‎ ‎∵点D的坐标为（6，1），DB⊥y轴，∴BD=6，∴S△BCD=×6•h=12，解得h=4。‎ ‎∵点C是双曲线第三象限上的动点，点D的纵坐标为1，∴点C的纵坐标为1－4= －3。‎ ‎∴，解得x= －2。∴点C的坐标为（－2，－3）。‎ 设直线CD的解析式为y=kx＋b，‎ 则，解得。‎ ‎∴直线CD的解析式为。‎ ‎（3）AB∥CD。理由如下：‎ ‎∵CA⊥x轴，DB⊥y轴，点C的坐标为（－2，－3），点D的坐标为（6，1），‎ ‎∴点A、B的坐标分别为A（－2，0），B（0，1）。‎ 设直线AB的解析式为y=mx+n，‎ 则，解得。‎ ‎∴直线AB的解析式为。‎ ‎∵AB、CD的解析式k都等于相等。‎ ‎∴AB与CD的位置关系是AB∥CD。‎ ‎【考点】反比例函数综合题，待定系数法，曲线上点的坐标与方程的关系，平行的判定。‎ ‎【分析】（1）把点D的坐标代入双曲线解析式，进行计算即可得解。‎ ‎（2）先根据点D的坐标求出BD的长度，再根据三角形的面积公式求出点C到BD的距离，然后求出点C的纵坐标，再代入反比例函数解析式求出点C的坐标，然后利用待定系数法求一次函数解析式解答。‎ ‎（3）根据题意求出点A、B的坐标，然后利用待定系数法求出直线AB的解析式，可知与直线 CD的解析式k值相等，所以AB、CD平行。‎ ‎7. （2012山东淄博9分）如图，正方形AOCB的边长为4，反比例函数的图象过点E（3，4）．‎ ‎（1）求反比例函数的解析式；‎ ‎（2）反比例函数的图象与线段BC交于点D，直线过点D，与线段AB相交于点F，求点F的坐标；‎ ‎（3）连接OF，OE，探究∠AOF与∠EOC的数量关系，并证明．‎ ‎【答案】解：（1）设反比例函数的解析式，‎ ‎∵反比例函数的图象过点E（3，4），∴，即。‎ ‎∴反比例函数的解析式。‎ ‎（2）∵正方形AOCB的边长为4，∴点D的横坐标为4，点F的纵坐标为4。‎ ‎　　　∵点D在反比例函数的图象上，∴点D的纵坐标为3，即D（4,3）。‎ ‎ ∵点D在直线上，∴，解得。‎ ‎　　　∴直线DF为。‎ ‎　　　将代入，得，解得。∴点F的坐标为（2，4）。‎ ‎（3）∠AOF＝∠EOC。证明如下：‎ 在CD上取CG=CF=2，连接OG，连接EG并延长交ｘ轴于点H。‎ ‎∵AO=CO=4，∠OAF=∠OCG=900，AF=CG=2，‎ ‎∴△OAF≌△OCG（SAS）。∴∠AOF=∠COG。‎ ‎∵∠EGB=∠HGC，∠B=∠GCH=900，BG=CG=2，‎ ‎∴△EGB≌△HGC（AAS）。∴EG=HG。‎ 设直线EG：，‎ ‎∵E（3，4），G（4，2），‎ ‎∴，解得，。‎ ‎∴直线EG：。‎ 令，得。∴H（5，0），OH=5。‎ 在Rｔ△AOF中，AO=4，AE=3，根据勾股定理，得OE=5。∴OC=OE。‎ ‎∴OG是等腰三角形底边EF上的中线。∴OG是等腰三角形顶角的平分线。‎ ‎∴∠EOG=∠GOH。∴∠EOG=∠GOC=∠AOF，即∠AOF＝∠EOC。‎ ‎【考点】反比例函数综合题，待定系数法，曲线上点的坐标与方程的关系，正方形的性质，全等三角形的判定和性质，勾股定理，等腰三角形的判定和性质。‎ ‎【分析】（1）将点E（3，4）代入待定的反比例函数解析式即可求得反比例函数的解析式。‎ ‎　　　　（2）求出点D的坐标代入即可求出直线DF的解析式，令 即可求得点F的坐标。‎ ‎（3）在CD上取CG=CF=2，连接OG，连接EG并延长交ｘ轴于点H。通过证△OAF≌△OCG（SAS）和△EGB≌△HGC（AAS）得到∠AOF=∠COG和EG=HG。求出直线EG的解析式从而得到点H的坐标，从而得到OH的长。在Rｔ△AOF中，应用勾股定理求得OE的长。因此得到OG是等腰三角形底边EF上的中线的结论，根据等腰三角形三线合一的性质得OG是等腰三角形顶角的平分线。从而得∠AOF＝∠EOC。‎ ‎8. （2012江西省8分）如图，等腰梯形ABCD放置在平面直角坐标系中，已知A（-2，0）、B（6，0）、D（0，3），反比例函数的图象经过点C．‎ ‎（1）求点C坐标和反比例函数的解析式；‎ ‎（2）将等腰梯形ABCD向上平移m个单位后，使点B恰好落在双曲线上，求m的值 ‎【答案】解：（1）过点C作CE⊥AB于点E，‎ ‎∵四边形ABCD是等腰梯形，‎ ‎∴AD=BC，DO=CE。‎ ‎∴△AOD≌△BEC（HL）。∴AO=BE=2。‎ ‎∵BO=6，∴DC=OE=4，∴C（4，3）。‎ 设反比例函数的解析式为（k≠0），‎ ‎∵反比例函数的图象经过点C，∴，解得k=12；‎ ‎∴反比例函数的解析式为。‎ ‎（2）将等腰梯形ABCD向上平移m个单位后得到梯形A′B′C′D′，‎ ‎∴点B′（6，m），‎ ‎∵点B′（6，m）恰好落在双曲线上，‎ ‎∴当x=6时，。‎ 即m=2。‎ ‎【考点】反比例函数综合题，等腰梯形的性质，全等三角形的判定和性质，待定系数法，曲线上点的坐标与方程的关系，平移的性质。‎ ‎【分析】（1）C点的纵坐标与D的纵坐标相同，过点C作CE⊥AB于点E，则△AOD≌△BEC，即可求得BE的长度，则OE的长度即可求得，即可求得C的横坐标，然后利用待定系数法即可求得反比例函数的解析式。‎ ‎（2）得出B′的坐标是（6，m），代入反比例函数的解析式，即可求出答案。‎