2011中考数学压轴题试题及答案选 22页

11 中考数学压轴题试题及答案选 1、（11 福州）如图所示，在平面直角坐标系 xOy 中，正方形 OABC 的边长为 2cm，点 A、C 分别在 y 轴的负半轴和 x 轴的正半轴上，抛物线 y=ax2+bx+c 经过点 A、B 和 D . （1）求抛物线的解析式. （2）如果点 P 由点 A 出发沿 AB 边以 2cm/s 的速度向点 B 运动，同 时点 Q 由点 B 出发沿 BC 边以 1cm/s 的速度向点 C 运动，当其中一点到达终点时，另一点也随之停 止运动. 设 S=PQ2(cm2) ①试求出 S 与运动时间 t 之间的函数关系式，并写出 t 的取值范围； ②当 S 取 时，在抛物线上是否存在点 R，使得以 P、B、Q、R 为顶点的四边形是平行四边形? 如果存在，求出 R 点的坐标；如果不存在，请说明理由. （3）在抛物线的对称轴上求点 M，使得 M 到 D、A 的距离之差最大，求出点 M 的坐标. 解: (1)据题意知: A(0, －2), B(2, －2) ，D（4，— ）, 则 解得 ∴抛物线的解析式为: ----------------------------4 分 (2) ①由图象知: PB=2－2t, BQ= t, ∴S=PQ2=PB2+BQ2=(2－2t)2 + t2 , 即 S=5t2－8t+4 (0≤t≤1) --------------------6 分 ②假设存在点 R, 可构成以 P、B、R、Q 为顶点的平行四边形. ∵S=5t2－8t+4 (0≤t≤1), ∴当 S= 时, 5t2－8t+4= ,得 20t2－32t+11=0, 解得 t = ，t = （不合题意，舍去）-------------------------------7 分 此时点 P 的坐标为（1，-2），Q 点的坐标为（2，— ） 若 R 点存在，分情况讨论: 2(4, )3 − 5 4 3 2 23 1 6 1 2 −−= xxy 4 5 4 5 2 1 10 11 2 3 （第 22 题） 【A】假设 R 在 BQ 的右边, 这时 QR PB, 则，R 的横坐标为 3, R 的纵坐标为— 即 R (3, － )，代入 , 左右两边相等， ∴这时存在 R(3, － )满足题意. 【B】假设 R 在 BQ 的左边, 这时 PR QB, 则：R 的横坐标为 1, 纵坐标为－ 即(1, － ) 代入 , 左右两边不相等, R 不在抛物线上. 【C】假设 R 在 PB 的下方, 这时 PR QB, 则：R(1，— )代入, 左右不相等, ∴R 不在抛物线上. 综上所述, 存点一点 R(3, － )满足题意. 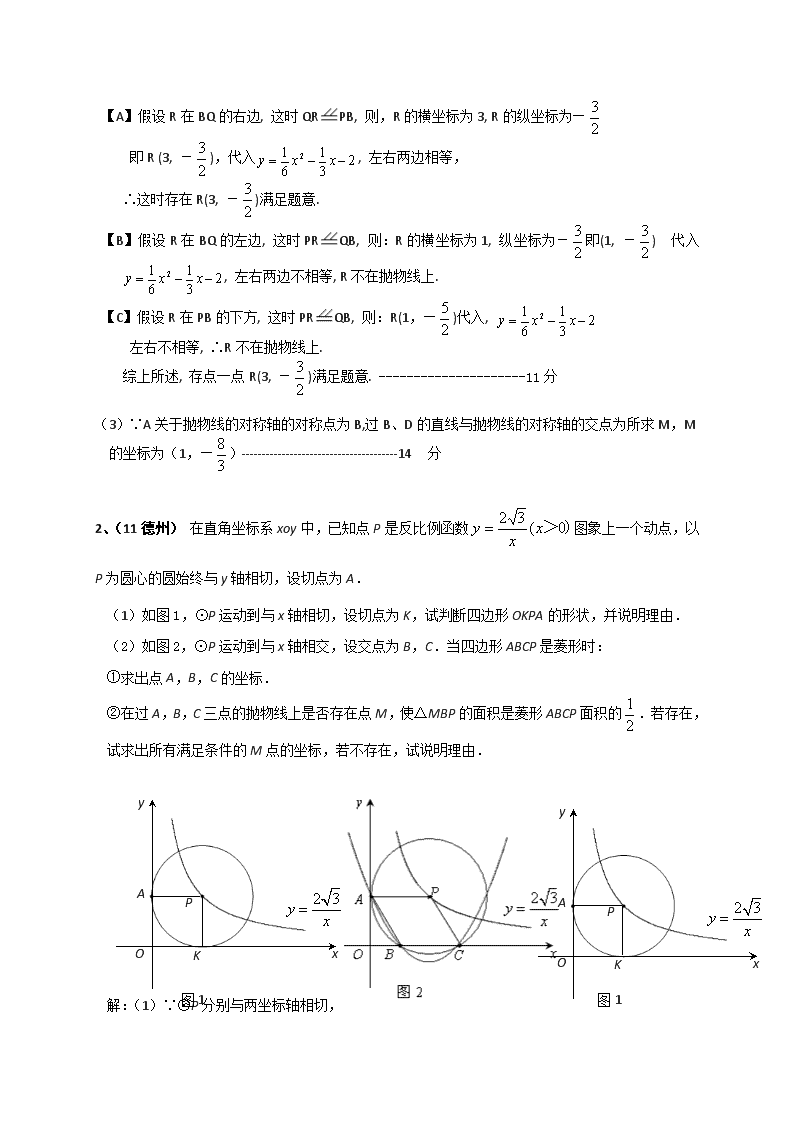---------------------11 分 （3）∵A 关于抛物线的对称轴的对称点为 B,过 B、D 的直线与抛物线的对称轴的交点为所求 M，M 的坐标为（1，— ）---------------------------------------14 分 2、（11 德州） 在直角坐标系 xoy 中，已知点 P 是反比例函数 图象上一个动点，以 P 为圆心的圆始终与 y 轴相切，设切点为 A． （1）如图 1，⊙P 运动到与 x 轴相切，设切点为 K，试判断四边形 OKPA 的形状，并说明理由． （2）如图 2，⊙P 运动到与 x 轴相交，设交点为 B，C．当四边形 ABCP 是菱形时： ①求出点 A，B，C 的坐标． ②在过 A，B，C 三点的抛物线上是否存在点 M，使△MBP 的面积是菱形 ABCP 面积的 ．若存在， 试求出所有满足条件的 M 点的坐标，若不存在，试说明理由． 解：（1）∵⊙P 分别与两坐标轴相切， 2 3 2 3 23 1 6 1 2 −−= xxy 2 3 2 3 2 3 23 1 6 1 2 −−= xxy 2 5 23 1 6 1 2 −−= xxy 2 3 3 8 ）＞0(32 xxy = 2 1 A P 2 3y x = x y KO 图 1 图 1 A P 2 3y x = x y KO ∴ PA⊥OA，PK⊥OK． ∴∠PAO=∠OKP=90°． 又∵∠AOK=90°， ∴ ∠PAO=∠OKP=∠AOK=90°． ∴四边形 OKPA 是矩形． 又∵OA=OK， ∴四边形 OKPA 是正方形．……………………2 分 （2）①连接 PB，设点 P 的横坐标为 x，则其纵坐标为 ． 过点 P 作 PG⊥BC 于 G． ∵四边形 ABCP 为菱形， ∴BC=PA=PB=PC． ∴△PBC 为等边三角形． 在 Rt△PBG 中，∠PBG=60°，PB=PA=x， PG= ． sin∠PBG= ，即 ． 解之得：x=±2（负值舍去）． ∴ PG= ，PA=BC=2．……………………4 分 易知四边形 OGPA 是矩形，PA=OG=2，BG=CG=1， ∴OB=OG－BG=1，OC=OG+GC=3． ∴ A（0， ），B（1，0） C（3，0）．……………………6 分 设二次函数解析式为：y=ax2+bx+c． 据题意得： 解之得：a= ， b= ， c= ． ∴二次函数关系式为： ．……………………9 分 ②解法一：设直线 BP 的解析式为：y=ux+v，据题意得： x 32 x 32 PB PG 2 3 3 2 x x = 3 3 0 9 3 0 3 a b c a b c c  + + =  + + =  = 3 3 4 3 3 − 3 23 4 3 33 3y x x= − + 0 2 3 u v u v + = + = O A P 2 3y x = x y B C 图 2 G M 解之得：u= ， v= ． ∴直线 BP 的解析式为： ． 过点 A 作直线 AM∥PB，则可得直线 AM 的解析式为： ． 解方程组： 得： ； ． 过点 C 作直线 CM∥PB，则可设直线 CM 的解析式为： ． ∴0= ． ∴ ． ∴直线 CM 的解析式为： ． 解方程组： 得： ； ． 综上可知，满足条件的 M 的坐标有四个， 分别为：（0， ），（3，0），（4， ），（7， ）．…………………12 分 解法二：∵ ， ∴A（0， ），C（3，0）显然满足条件． 延长 AP 交抛物线于点 M，由抛物线与圆的轴对称性可知，PM=PA． 又∵AM∥BC， ∴ ． ∴点 M 的纵坐标为 ． 又点 M 的横坐标为 AM=PA+PM=2+2=4． ∴点 M（4， ）符合要求． 3 3 3− 3 3 3y x= − 3 3y x= + 2 3 3 3 4 3 33 3 y x y x x  = + = − + 1 1 0 3 x y = = 2 2 7 8 3 x y = = 3y x t= + 3 3 t+ 3 3t = − 3 3 3y x= − 2 3 3 3 3 4 3 33 3 y x y x x  = − = − + 1 1 3 0 x y =  = 2 2 4 3 x y = = 3 3 8 3 1 2PAB PBC PABCS S S∆ ∆= =  3 1 2PBM PBA PABCS S S∆ ∆= =  3 3 点（7， ）的求法同解法一． 综上可知，满足条件的 M 的坐标有四个， 分别为：（0， ），（3，0），（4， ），（7， ）．…………………12 分 解法三：延长 AP 交抛物线于点 M，由抛物线与圆的轴对称性可知，PM=PA． 又∵AM∥BC， ∴ ． ∴点 M 的纵坐标为 ． 即 ． 解得： （舍）， ． ∴点 M 的坐标为（4， ）． 点（7， ）的求法同解法一． 综上可知，满足条件的 M 的坐标有四个， 分别为：（0， ），（3，0），（4， ），（7， ）．…………………12 分 3、（11 义乌）已知二次函数的图象经过 A（2，0）、C(0，12) 两点，且对称轴为直线 x=4. 设顶点为 点 P，与 x 轴的另一交点为点 B. （1）求二次函数的解析式及顶点 P 的坐标； （2）如图 1，在直线 y=2x 上是否存在点 D，使四边形 OPBD 为等腰梯形？若存在，求出点 D 的 坐标；若不存在，请说明理由； （3）如图 2，点 M 是线段 OP 上的一个动点（O、P 两点除外），以每秒 个单位长度的速度由 点 P 向点 O 运动，过点 M 作直线 MN∥x 轴，交 PB 于点 N. 将△PMN 沿直线 MN 对折，得 到△P1MN. 在动点 M 的运动过程中，设△P1MN 与梯形 OMNB 的重叠部分的面积为 S，运 动时间为 t 秒. 求 S 关于 t 的函数关系式. 解 ： （ 1 ） 设二次函数的解析 式 为 y=ax2+bx+c 由 题 意 得 8 3 3 3 8 3 1 2PBM PBA PABCS S S∆ ∆= =  3 23 4 3 3 33 3x x− + = 1 0x = 2 4x = 3 8 3 3 3 8 3 2 O P C BA x y 图 1 图 2 M O A x P N C B y 解得 ∴二次函数的解析式为 y= x2－8x+12 ……………………………………………2 分 点 P 的坐标为（4，－4） …………………………………………………………3 分 （2）存在点 D，使四边形 OPBD 为等腰梯形. 理由如下： 当 y=0 时，x2-8x+12=0 ∴x1=2 ， x2=6 ∴点 B 的坐标为（6，0） 设直线 BP 的解析式为 y=kx+m 则 解得 ∴直线 BP 的解析式为 y=2x－12 ∴直线 OD∥BP………………………………………4 分 ∵顶点坐标 P（4， －4） ∴ OP=4 设 D(x，2x) 则 BD2=（2x）2+(6－x)2 当 BD=OP 时，（2x）2+(6－x)2=32 解得：x1= ，x 2=2…………………………………………………………………6 分 当 x2=2 时，OD=BP= ，四边形 OPBD 为平行四边形，舍去 ∴当 x= 时四边形 OPBD 为等腰梯形 …………………7 分 ∴当 D( ， )时，四边形 OPBD 为等腰梯形 ………8 分 （3）① 当 0＜t≤2 时， ∵运动速度为每秒 个单位长度，运动时间为 t 秒， 则 MP= t ∴PH=t，MH=t，HN= t ∴MN= t ∴S= t·t· = t2 ……………………10 分 ② 当 2＜t＜4 时，P1G=2t－4，P1H=t ∵MN∥OB ∴ ∽ ∴ ∴        =++ = =− 024 12 42 cba c a b    = −= = 12 8 1 c b a    −=+ =+ 44 06 mk mk    −= = 12 2 m k 2 5 2 52 5 2 5 2 5 4 2 2 2 1 2 3 2 3 2 1 4 3 EFP1∆ MNP1∆ 2 1 1 )( 1 1 HP GP S S MNP EFP = ∆ ∆ 2 2 )42( 4 3 1 t t t S EFP −=∆ xP1M AO B C P N y H x P1 M AO B C P N G H E F y DO xAO B C P y 图 1 图 2 图 3 x y M N xO C E A B F A B y C O … x O y A C B ∴ =3t2－12t+12 ∴S= t2－(3t2－12t+12)= － t2+12t－12 ∴ 当 0＜t≤2 时，S= t2 4、（11 金华）在平面直角坐标系中，如图 1，将 个边长为 1 的正方形并排组成矩形 OABC, 相邻两 边 OA 和 OC 分别落在 轴和 轴的正半轴上, 设抛物线 （ ＜0）过矩形顶点 B、 C. （1）当 n=1 时，如果 =-1，试求 b 的值； （2）当 n=2 时，如图 2，在矩形 OABC 上方作一边长为 1 的正方形 EFMN，使 EF 在线段 CB 上，如 果 M，N 两点也在抛物线上，求出此时抛物线的解析式； （3）将矩形 OABC 绕点 O 顺时针旋转，使得点 B 落到 轴的正半轴上，如果该抛物线同时经过原 点 O.①试求当 n=3 时 a 的值； ②直接写出 关于 的关系式． 23.(本题 10 分) （1）由题意可知，抛物线对称轴为直线 x= ， ∴ ,得 b= 1； ……2 分 （2）设所求抛物线解析式为 ， 由对称性可知抛物线经过点 B（2，1）和点 M（ ，2） ∴ 解得 ∴所求抛物线解析式为 ；……4 分 （3）①当 n=3 时，OC=1，BC=3， 设所求抛物线解析式为 ， 过 C 作 CD⊥OB 于点 D，则 Rt△OCD∽Rt△CBD， ∴ , 设 OD=t，则 CD=3t， ∵ ， EFPS 1∆ 4 3 4 9 4 3 n x y 2y ax bx c= + + a a x a n 1 2 1 2 2 b a − = 2 1y ax bx= + + 1 2 1 4 2 1 1 12 1.4 2 a b a b = + + = + + ， 4 ,3 8.3 a b  = −  = 24 8 13 3y x x= − + + 2y ax bx= + 1 3 OD OC CD BC = = 2 2 2OD CD OC+ = x y O A B C D x y O C E A B M N F y xO C A B ∴ ， ∴ , ∴C（ ， ）, 又 B（ ，0）， ∴把 B 、C 坐标代入抛物线解析式，得 解得:a= ； ……2 分 ② . ……2 分 5、（11 金华）如图，在平面直角坐标系中，点 A（10，0），以 OA 为直径在第一象限内作半圆 C， 点 B 是该半圆周上一动点，连结 OB、AB，并延长 AB 至点 D，使 DB=AB，过点 D 作 x 轴垂线，分 别交 x 轴、直线 OB 于点 E、F，点 E 为垂足，连结 CF． （1）当∠AOB=30°时，求弧 AB 的长度； （2）当 DE=8 时，求线段 EF 的长； （3）在点 B 运动过程中，是否存在以点 E、C、F 为顶点的三角形与△AOB 相似，若存在，请求出此 时点 E 的坐标；若不存在，请说明理由． （1）连结 BC, ∵A（10，0）, ∴OA=10 ,CA=5, ∵∠AOB=30°, ∴∠ACB=2∠AOB=60°, ∴弧 AB 的长= ; ……4 分 （2）连结 OD, ∵OA 是⊙C 直径, ∴∠OBA=90°, 又∵AB=BD, ∴OB 是 AD 的垂直平分线, ∴OD=OA=10, 在 Rt△ODE 中， OE= , ∴AE=AO－OE=10-6=4, 由 ∠AOB=∠ADE=90°-∠OAB，∠OEF=∠DEA， 得△OEF∽△DEA, ∴ ,即 ，∴EF=3；……4 分 （3）设 OE=x， ①当交点 E 在 O，C 之间时，由以点 E、C、F 为顶点的三角 形与△AOB 相似，有∠ECF=∠BOA 或∠ECF=∠OAB， 当∠ECF=∠BOA 时，此时△OCF 为等腰三角形，点 E 为 OC 2 2 2(3 ) 1t t+ = 1 10 10 10t = = 10 10 3 1010 10 0 10 10 3 1 1010 .10 10 10 a b a b  = + = + ， 10 3 − 2 1na n += − 3 5 180 560 ππ =×× =− 22 DEOD 6810 22 =− OE EF DE AE = 68 4 EF= 第 24 题图 O B D EC F x y A O B D EC F x y A O B D F CE A x y 中点，即 OE= ， ∴E1（ ，0）； 当∠ECF=∠OAB 时，有 CE=5-x, AE=10-x， ∴CF∥AB,有 CF= , ∵△ECF∽△EAD, ∴ ,即 ,解得： , ∴E2（ ，0）; ②当交点 E 在点 C 的右侧时， ∵∠ECF＞∠BOA， ∴要使△ECF 与△BAO 相似，只能使∠ECF=∠BAO， 连结 BE， ∵BE 为 Rt△ADE 斜边上的中线， ∴BE=AB=BD, ∴∠BEA=∠BAO, ∴∠BEA=∠ECF, ∴CF∥BE, ∴ , ∵∠ECF=∠BAO, ∠FEC=∠DEA=Rt∠， ∴△CEF∽△AED, ∴ , 而 AD=2BE, ∴ , 即 , 解得 , ＜0（舍去）， ∴E3（ ，0）; ③当交点 E 在点 O 的左侧时， ∵∠BOA=∠EOF＞∠ECF . ∴要使△ECF 与△BAO 相似，只能使∠ECF=∠BAO 连结 BE，得 BE= =AB，∠BEA=∠BAO ∴∠ECF=∠BEA, ∴CF∥BE, ∴ , 又∵∠ECF=∠BAO, ∠FEC=∠DEA=Rt∠， 2 5 2 5 1 2 AB AD CF AE CE = 5 1 10 4 x x − =− 3 10=x 3 10 OE OC BE CF = CF CE AD AE = 2 OC CE OE AE = 5 5 2 10 x x x −= − 4 1755 1 +=x 4 1755 2 −=x 4 1755 + AD2 1 OE OC BE CF = O B D F CE A x y O B D F C E A x y O B D F CE A x y A B C D l1 l2 l3 l4 h1 h2 h3 ∴△CEF∽△AED, ∴ ， 而 AD=2BE, ∴ , ∴ , 解得 , ＜0（舍去）, ∵点 E 在 x 轴负半轴上, ∴E4（ ，0）, 综上所述：存在以点 E、C、F 为顶点的三角形与△AOB 相似,此时点 E 坐标为： （ ，0）、 （ ，0）、 （ ，0）、 （ ，0）．……4 分 6、（11 安徽如图，正方形 ABCD 的四个顶点分别在四条平行线 l1、l2、l3、l4 上，这四条直线中相邻 两条之间的距离依次为 h1、h2、h3(h1＞0，h2＞0，h3＞0)． (1)求证：h1＝h2； 【证】 (2)设正方形 ABCD 的面积为 S，求证：S＝(h1＋h2)2＋h12； 【证】 (3)若 3 2h1＋h2＝1，当 h1 变化时，说明正方形 ABCD 的面积 S 随 h1 的变化情况． 【解】 （1）过 A 点作 AF⊥l3 分别交 l2、l3 于点 E、F，过 C 点作 CH⊥l2 分别交 l2、l3 于点 H、G，证△ABE≌△ CDG 即可. （2）易证△ABE≌△BCH≌△CDG≌△DAF,且两直角边长分别为 h1、h1+h2,四边形 EFGH 是边长为 h2 的 正方形， 所以 . (3)由题意，得 所以 又 解得 0＜h1＜ AD CF AE CE = 2 OC CE OE AE = 5 +5 2 10+ x x x = 4 1755 1 +−=x 4 1755 2 −−=x 4 1755 − 1E 2 5 2E 3 10 3E 4 1755 + 4E 4 1755 − ( ) 2 1 2 21 2 221 2 1 2 2211 )(222 14 hhhhhhhhhhhS ++=++=++×= 12 3 2 1 hh −= 5 4 5 2 4 5 14 5 2 31 2 1 1 2 1 2 1 2 11 +     −= +−=+     −+= h hhhhhS    〉− 〉 02 31 0 1 1 h h 3 2 ∴当 0＜h1＜ 时，S 随 h1 的增大而减小； 当 h1= 时，S 取得最小值 ； 当 ＜h1＜ 时，S 随 h1 的增大而增大. 7、（11 日照）如图，抛物线 y=ax2+bx（a 0）与双曲线 y= 相交于点 A，B. 已知点 B 的坐标为 （-2，-2），点 A 在第一象限内，且 tan∠AOx=4. 过点 A 作直线 AC∥x 轴，交抛物线于另一点 C． （1）求双曲线和抛物线的解析式； （2）计算△ABC 的面积； （3）在抛物线上是否存在点 D，使△ABD 的面积等于△ABC 的面 积．若存在，请你写出点 D 的坐标；若不存在，请你说明理由． 8、（11 威海）如图，抛物线 y=ax2＋bx＋c 交 x 轴于点 A（－3，0），点 B（1，0），交 y 轴于点 E（0，－ 3）。点 C 是点 A 关于点 B 的对称点，点 F 是线段 BC 的中点，直线 l 过点 F 且与 y 轴平行。直线 y= －x＋m 过点 C，交 y 轴于 D 点。 ⑴求抛物线的函数表达式； ⑵点 K 为线段 AB 上一动点，过点 K 作 x 轴的垂线与直线 CD 交于点 H，与抛物线交于点 G， 求线段 HG 长度的最大值； ⑶在直线 l 上取点 M，在抛物线上取点 N，使以点 A，C，M，N 为顶点的四边形是平行四边 形，求点 N 的坐标。 9、（11 广州）已知关于 x 的二次函数 y=ax2+bx+c(a>0)的图象经过点 C(0,1)，且与 x 轴交于不同的 两点 A、B，点 A 的坐标是（1，0） （1）求 c 的值； 5 2 5 2 5 4 5 2 3 2 x k A B C DH E F G K O x y l 图① A B C DH E F G K O x y l 备用图 （2）求 a 的取值范围； （3）该二次函数的图象与直线 y=1 交于 C、D 两点，设 A、B、C、D 四点构成的四边形的对角线相 交于点 P，记△PCD 的面积为 S1，△PAB 的面积为 S2，当 0 ( ) ( )2 22 21 4 2 1 4 2 1 1a a a a a a a a∆ = − + − = + + − = − + = −   a 0a > 1a ≠ 0 1a< < 1 1 12 2 a ax a a − − += − = > 1 12 12 a aAB a a + − = − =   1y = ( )2 1 1y ax a x= − + + ( )2 1 0ax a x− + = 1 2 10, ax x a += = 1 aCD a += 1 2 PCD PAB ACD CABS S S S S S∆ ∆ ∆ ∆− = − = − 1 1 2 2CD OC AB OC× × − × × 1 1 1 11 12 2 2 a a a + −× × − × × 1 2S S− 2 α α 2 x y P D B C O A （1）证明：∵ AB 是⊙O 的直径 ∴ ∠ACB=90° ∵ ∠DCE=90° ∴∠ACB＋∠DCE=180° ∴ B、C、E 三点共线。 (2)证明：连接 ON、AE、BD，延长 BD 交 AE 于点 F ∵ ∠ABC=45°，∠ACB=90° ∴ BC=AC，又∠ACB=∠DCE=90°，DC=EC ∴ △BCD≌△ACE ∴ BD=AE，∠DBC=∠CAE ∴∠DBC＋∠AEC=∠CAE＋∠AEC=90° ∴ BF⊥AE ∵ AO=OB，AN=ND ∴ ON= BD，ON∥BD ∵ AO=OB，EM=MB ∴ OM= AE，OM∥AE ∴ OM=ON，OM⊥ON ∴ ∠OMN=45°，又 cos∠OMN= ∴ (3) 成立，证明同（2）。 11、（11 舟山）已知直线 （ ＜0）分别交 轴、 轴于 A、B 两点，线段 OA 上有一动点 P 由原点 O 向点 A 运动，速度为每秒 1 个单位长度，过点 P 作 轴的垂线交直线 AB 于点 C，设运 动时间为 秒． 1 2 1 2 OM MN 2MN OM= 1 1 12M N OM= 3+= kxy k x y x t F N1 M1 D O B C A E F N M DO B C A E （1）当 时，线段 OA 上另有一动点 Q 由点 A 向点 O 运动，它与点 P 以相同速度同时出发， 当点 P 到达点 A 时两点同时停止运动（如图 1）． ① 直接写出 ＝1 秒时 C、Q 两点的坐标； ② 若以 Q、C、A 为顶点的三角形与△AOB 相似 ，求 的值． （2）当 时，设以 C 为顶点的抛物线 与直线 AB 的另一交点为 D（如图 2）， ① 求 CD 的长； ② 设△COD 的 OC 边上的高为 ，当 为何值时， 的值最大？ 1−=k t t 4 3−=k nmxy ++= 2)( h t h B AO P C x y 1 1 D （第 24 题图 2）（第 24 题图 1） B AO P C Q x y 1 1 12、（11 济宁）如图，在平面直角坐标系中，顶点为（ ， ）的抛物线交 轴于 点，交 轴于 ， 两点（点 在点 的左侧）. 已知 点坐标为（ ， ）. （1）求此抛物线的解析式； （2）过点 作线段 的垂线交抛物线于点 ， 如果以点 为圆心的圆与直线 相切，请 判断抛物线的对称轴 与⊙ 有怎样的位置关系，并给出证明； （3）已知点 是抛物线上的一个动点，且位于 ， 两点之间，问：当点 运动到什么位置 时， 的面积最大？并求出此时 点的坐标和 的最大面积. （1）解：设抛物线为 . ∵抛物线经过点 （0，3），∴ .∴ . ∴抛物线为 . ……………………………3 分 (2) 答： 与⊙ 相交. …………………………………………………………………4 分 证明：当 时， ， . ∴ 为（2，0）， 为（6，0）.∴ . 设⊙ 与 相切于点 ，连接 ，则 . ∵ ，∴ . 又∵ ，∴ .∴ ∽ . ∴ .∴ .∴ .…………………………6 分 ∵抛物线的对称轴 为 ，∴ 点到 的距离为 2. ∴抛物线的对称轴 与⊙ 相交. ……………………………………………7 分 4 1− y A x B C B C A 0 3 B AB D C BD l C P A C P PAC∆ P PAC∆ 2( 4) 1y a x= − − A 23 (0 4) 1a= − − 1 4a = 2 21 1( 4) 1 2 34 4y x x x= − − = − + l C 21 ( 4) 1 04 x − − = 1 2x = 2 6x = B C 2 23 2 13AB = + = C BD E CE 90BEC AOB∠ = ° = ∠ 90ABD∠ = ° 90CBE ABO∠ = °− ∠ 90BAO ABO∠ = °− ∠ BAO CBE∠ = ∠ AOB∆ BEC∆ CE BC OB AB = 6 2 2 13 CE −= 8 2 13 CE = > l 4x = C l l C A x y BO C D (第 23 题) (3) 解：如图，过点 作平行于 轴的直线交 于点 . 可求出 的解析式为 .…………………………………………8 分 设 点的坐标为（ ， ），则 点的坐标为（ ， ）. ∴ . ∵ , ∴当 时， 的面积最大为 . 此时， 点的坐标为（3， ）. …………………………………………10 分 13、（11 菏泽）21. （本题 9 分）如图，抛物线 y＝1 2x2＋bx－2 与 x 轴交于 A，B 两点，与 y 轴交于 C 点，且 A(－1，0)． （1）求抛物线的解析式及顶点 D 的坐标； （2）判断 的形状，证明你的结论； （3）点 是 x 轴上的一个动点，当 MC＋MD 的值最 小时，求 m 的值． （1）把点 A(－1，0)的坐标代入抛物线的解析式 y＝1 2x2＋bx－ 2， 整理后解得 ， P y AC Q AC 1 32y x= − + P m 21 2 34 m m− + Q m 1 32 m− + 2 21 1 1 33 ( 2 3)2 4 4 2PQ m m m m m= − + − − + = − + 2 21 1 3 3 27( ) 6 ( 3)2 4 2 4 4PAC PAQ PCQS S S m m m∆ ∆ ∆= + = × − + × = − − + 3m = PAC∆ 27 4 P 3 4 − ABC△ ( 0)M m， 3 2b = − A x y BO ht tp: // w w w. gz sx w. ne t/ C D (第 23 题) E P Q A B C D x y O （第 21 题图） 1 1 1− 所以抛物线的解析式为 ．…………………………………2 分 顶点 ． …………………………………3 分 （2） ． ， ， ． 是直角三角形． …………………………………6 分 （3）作出点 关于 轴的对称点 ，则 ， ．连接 交 轴于点 ， 根据轴对称性及两点之间线段最短可知， 的值最小． 设抛物线的对称轴交 轴于点 ． ． ． ． ．…………………………………10 分 说明:此处求出 、D 的解析式后，再求与 x 轴的交点坐标可同样给分. 14（11 成都）如图，在平面直角坐标系 中，△ABC 的 A、B 两个顶点在 x 轴上，顶点 C 在 y 轴 的 负 半 轴 上 ． 已 知 ， ， △ABC 的 面 积 ， 抛 物 线 经过 A、B、C 三点。 (1)求此抛物线的函数表达式； (2)设 E 是 y 轴右侧抛物线上异于点 B 的一个动点，过点 E 作 x 轴的平行线交抛物线于另一点 F，过点 F 作 FG 垂直于 x 轴于点 G，再过点 E 作 EH 垂直于 x 轴于点 H，得到矩形 EFGH．则在点 E 的 运动过程中，当矩形 EFGH 为正方形时，求出该正方形的边长； (3)在抛物线上是否存在异于 B、C 的点 M，使△MBC 中 BC 边上的高为 ？若存在，求出点 M 的坐标；若不存在，请说明理由． 3 25 2 8  −  ， 24 41m∴ = 21 3 22 2y x x= − − D 5AB = 2 2 2 5AC OA OC= + = 2 2 2 20BC OC OB= + = 2 2 2AC BC AB∴ + = ABC∴△ C x C′ (0 2)C′ ， 2OC′ = C D′ x M MC MD+ x E C OM DEM′△ ∽△ OM OC EM ED ′∴ = 2 3 25 2 8 m m ∴ = − 'C xOy : 1:5OA OB = OB OC= 15ABCS∆ = 2 ( 0)y ax bx c a= + + ≠ 7 2 15（11 福州） 已知,如图 11,二次函数 图象的顶点为 ,与 轴交于 、 两点( 在 点右侧),点 、 关于直线 : 对称. (1)求 、 两点坐标,并证明点 在直线 上; (2)求二次函数解析式; (3)过点 作直线 ∥ 交直线 于 点, 、 分别为直线 和直线 上的两个动点,连 接 、 、 ,求 和的最小值. 解:(1)依题意,得 解得 , ∵ 点在 点右侧 ∴ 点坐标为 , 点坐标为 ∵直线 : 当 时, ∴点 在直线 上 (2)∵点 、 关于过 点的直线 : 对称 ∴ 过顶点 作 交 于 点 则 , ∴顶点 代入二次函数解析式,解得 ∴二次函数解析式为 (3)直线 的解析式为 直线 的解析式为 由 解得 即 ,则 ∵点 、 关于直线 对称 ∴ 的最小值是 , 过点 作直线 的对称点 ,连接 ,交直线 于 2 2 3y ax ax a= + − ( 0)a ≠ H x A B B A H B l 3 33y x= + A B A l B BK AH l K M N AH l HN NM MK HN NM MK+ + 2 2 3 0ax ax a+ − = ( 0)a ≠ 1 3x = − 2 1x = B A A ( 3 0)− , B (1 0), l 3 33y x= + 3x = − 3 ( 3) 3 03y = × − + = A l H B A l 3 33y x= + 4AH AB= = H HC AB⊥ AB C 1 22AC AB= = 2 3HC = ( 1,2 3)H − 3 2a = − 23 3 332 2y x x= − − + AH 3 3 3y x= + BK 3 3y x= − 3 33 3 3 y x y x  = +  = − { 3 2 3 x y = = (3,2 3)K 4BK = H B AK HN MN+ MB 2 3KD KE= = K AH Q QK AH E A B K H x y O l 图 11 A B K H x y O l 备用图 11 A B K H x y C O 则 , , ∴ 的最小值是 ,即 的长是 的最小值 ∵ ∥ ∴ 由勾股定理得 ∴ 的最小值为 （不同解法参照给分） 16、（11 泉州）在直角坐标系 xoy 中，已知点 P 是反比例函数 图象上一个动点，以 P 为圆心的圆始终与 y 轴相切，设切点为 A． （1）如图 1，⊙P 运动到与 x 轴相切，设切点为 K，试判断四边形 OKPA 的形状，并说明理由． （2）如图 2，⊙P 运动到与 x 轴相交，设交点为 B，C．当四边形 ABCP 是菱形时： ①求出点 A，B，C 的坐标． ②在过 A，B，C 三点的抛物线上是否存在点 M，使△MBP 的面积是菱形 ABCP 面积的 ．若存在， 试求出所有满足条件的 M 点的坐标，若不存在，试说明理由． 解：（1）∵⊙P 分别与两坐标轴相切， ∴ PA⊥OA，PK⊥OK． ∴∠PAO=∠OKP=90°． 又∵∠AOK=90°， ∴ ∠PAO=∠OKP=∠AOK=90°． ∴四边形 OKPA 是矩形． 又∵OA=OK， ∴四边形 OKPA 是正方形．……………………2 分 QM MK= 2 3QE EK= = AE QK⊥ BM MK+ BQ BQ HN NM MK+ + BK AH 90BKQ HEQ∠ = ∠ = ° 8QB = HN NM MK+ + 8 ）＞0(32 xxy = 2 1 A B K H N M D E Q x y O l A P 2 3y x = x y KO 第 25 题 图 1 （2）①连接 PB，设点 P 的横坐标为 x，则其纵坐标为 ． 过点 P 作 PG⊥BC 于 G． ∵四边形 ABCP 为菱形， ∴BC=PA=PB=PC． ∴△PBC 为等边三角形． 在 Rt△PBG 中，∠PBG=60°，PB=PA=x， PG= ． sin∠PBG= ，即 ． 解之得：x=±2（负值舍去）． ∴ PG= ，PA=BC=2．……………………4 分 易知四边形 OGPA 是矩形，PA=OG=2，BG=CG=1， ∴OB=OG－BG=1，OC=OG+GC=3． ∴ A（0， ），B（1，0） C（3，0）．……………………6 分 设二次函数解析式为：y=ax2+bx+c． 据题意得： 解之得：a= ， b= ， c= ． ∴二次函数关系式为： ．……………………9 分 ②解法一：设直线 BP 的解析式为：y=ux+v，据题意得： 解之得：u= ， v= ． ∴直线 BP 的解析式为： ． 过点 A 作直线 AM∥PB，则可得直线 AM 的解析式为： ． x 32 x 32 PB PG 2 3 3 2 x x = 3 3 0 9 3 0 3 a b c a b c c  + + =  + + =  = 3 3 4 3 3 − 3 23 4 3 33 3y x x= − + 0 2 3 u v u v + = + = 3 3 3− 3 3 3y x= − 3 3y x= + O A P 2 3y x = x y B C 图 2 G M 解方程组： 得： ； ． 过点 C 作直线 CM∥PB，则可设直线 CM 的解析式为： ． ∴0= ． ∴ ． ∴直线 CM 的解析式为： ． 解方程组： 得： ； ． 综上可知，满足条件的 M 的坐标有四个， 分别为：（0， ），（3，0），（4， ），（7， ）．…………………12 分 解法二：∵ ， ∴A（0， ），C（3，0）显然满足条件． 延长 AP 交抛物线于点 M，由抛物线与圆的轴对称性可知，PM=PA． 又∵AM∥BC， ∴ ． ∴点 M 的纵坐标为 ． 又点 M 的横坐标为 AM=PA+PM=2+2=4． ∴点 M（4， ）符合要求． 点（7， ）的求法同解法一． 综上可知，满足条件的 M 的坐标有四个， 分别为：（0， ），（3，0），（4， ），（7， ）．…………………12 分 解法三：延长 AP 交抛物线于点 M，由抛物线与圆的轴对称性可知，PM=PA． 2 3 3 3 4 3 33 3 y x y x x  = + = − + 1 1 0 3 x y = = 2 2 7 8 3 x y = = 3y x t= + 3 3 t+ 3 3t = − 3 3 3y x= − 2 3 3 3 3 4 3 33 3 y x y x x  = − = − + 1 1 3 0 x y =  = 2 2 4 3 x y = = 3 3 8 3 1 2PAB PBC PABCS S S∆ ∆= =  3 1 2PBM PBA PABCS S S∆ ∆= =  3 3 8 3 3 3 8 3 又∵AM∥BC， ∴ ． ∴点 M 的纵坐标为 ． 即 ． 解得： （舍）， ． ∴点 M 的坐标为（4， ）． 点（7， ）的求法同解法一． 综上可知，满足条件的 M 的坐标有四个， 分别为：（0， ），（3，0），（4， ），（7， ）．…………………12 分 1 2PBM PBA PABCS S S∆ ∆= =  3 23 4 3 3 33 3x x− + = 1 0x = 2 4x = 3 8 3 3 3 8 3