中考复习专题 实际应用题 19页

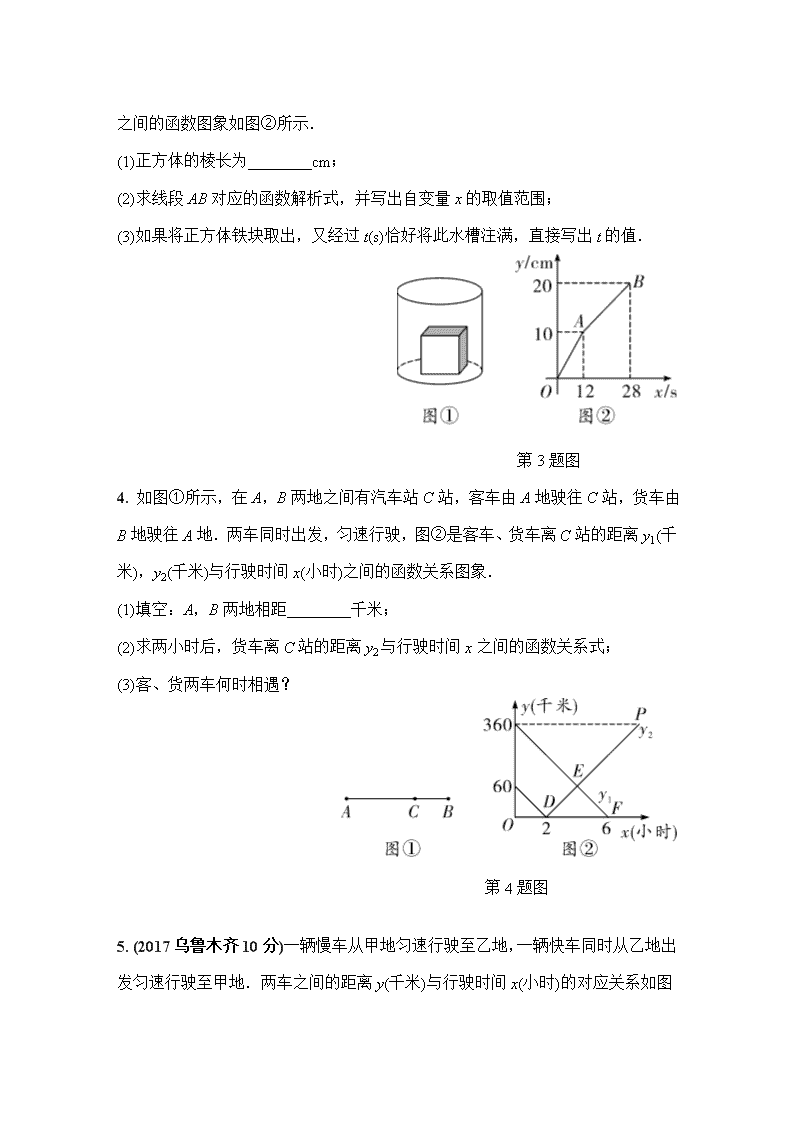
中考复习专题： 实际应用题 类型一　一次函数图象型问题 ‎1. 某游泳池一天要经过“注水—保持—排水”三个过程，如图，图中折线表示的是游泳池在一天某一时间段内池中水量y(m3)与时间x(min)之间的关系．‎ ‎(1)求排水阶段y与x之间的函数关系式，并写出x的取值范围；‎ ‎(2)求水量不超过最大水量的一半值的时间一共有多少分钟．‎ ‎ 第1题图 ‎2. (2017衢州8分)“五·一”期间，小明一家乘坐高铁前往某市旅游，计划第二天租用新能源汽车自驾出游．‎ 根据以上信息，解答下列问题：‎ ‎(1)设租车时间为x小时，租用甲公司的车所需费用为y1元，租用乙公司的车所需费用为y2元，分别求出y1、y2关于x的函数表达式；‎ ‎(2)请你帮助小明计算并选择哪个出游方案合算．‎ 第2题图 ‎3. (2017吉林省卷8分)如图①，一个正方体铁块放置在圆柱形水槽内，现以一定的速度往水槽中注水，28 s时注满水槽．水槽内水面的高度y(cm)与注水时间x ‎(s)之间的函数图象如图②所示．‎ ‎(1)正方体的棱长为________cm；‎ ‎(2)求线段AB对应的函数解析式，并写出自变量x的取值范围；‎ ‎(3)如果将正方体铁块取出，又经过t(s)恰好将此水槽注满，直接写出t的值．‎ 第3题图 ‎4. 如图①所示，在A，B两地之间有汽车站C站，客车由A地驶往C站，货车由B地驶往A地．两车同时出发，匀速行驶，图②是客车、货车离C站的距离y1(千米)，y2(千米)与行驶时间x(小时)之间的函数关系图象．‎ ‎(1)填空：A，B两地相距________千米；‎ ‎(2)求两小时后，货车离C站的距离y2与行驶时间x之间的函数关系式；‎ ‎(3)客、货两车何时相遇？‎ 第4题图 ‎5. (2017乌鲁木齐10分)一辆慢车从甲地匀速行驶至乙地，一辆快车同时从乙地出发匀速行驶至甲地．两车之间的距离y(千米)与行驶时间x ‎(小时)的对应关系如图所示：‎ ‎(1)甲乙两地相距多远？‎ ‎(2)求快车和慢车的速度分别是多少？‎ ‎(3)求出两车相遇后y与x之间的函数关系式；‎ ‎(4)何时两车相距300千米．‎ 第5题图 答案 ‎1. 解：(1)设排水阶段y与x之间的函数关系式是y＝kx＋b，‎ 将(285，1500)，(300，0)代入得，，解得，‎ 即排水阶段y与x之间的函数关系式是y＝－100x＋30000，‎ 当y＝2000时，2000＝－100x＋30000，解得x＝280，‎ ‎∴x的取值范围是280≤x≤300；‎ ‎(2)设注水阶段y与x的函数关系式为y＝mx，将(30，1500)代入得，30m＝1500，解得m＝50，∴注水阶段y与x的函数关系式为y＝50x，‎ 当y＝1000时，1000＝50x，得x＝20，‎ 将y＝1000代入y＝－100x＋30000，得x＝290，‎ ‎∴水量不超过最大水量的一半值的时间一共有20＋(300－290)＝30(分钟)．‎ ‎2. 解：(1)由题意可知y1＝k1x＋80，且图象过点(1，95)，则有95＝k1＋80，‎ ‎∴k1＝15，∴y1＝15x＋80(x≥0)，由题意易得y2＝30x(x≥0)；‎ ‎(2)当y1＝y2时，解得x＝，‎ 当y1＞y2时，解得x<，‎ 当y1＜y2时，解得x>.‎ ‎∴当租车时间为小时，选择甲、乙公司一样合算；‎ 当租车时间小于小时，选择乙公司合算；‎ 当租车时间大于小时，选择甲公司合算．‎ ‎3. 解：(1)10；‎ ‎【解法提示】由题意可得12秒时，水槽内水面的高度为10 cm，12秒后水槽内高度变化趋势改变，故正方体的棱长为10 cm；‎ ‎(2)设线段AB对应的函数解析式为：‎ y＝kx＋b，‎ ‎∵图象过A(12，10)，B(28，20)，∴，解得，‎ ‎∴线段AB对应的函数解析式为：y＝x＋(12≤x≤28)；‎ ‎(3)4 s.‎ ‎【解法提示】∵没有正方体时，水面上升10 cm，所用时间为16 s，∴没有正方体的圆柱形水槽，注满需要用时间32 s，∴取出正方体铁块后，已经注水28 s，且注水速度一定，故还需要4 s才能注满圆柱形水槽，∴t＝4 s.‎ ‎4. 解：(1)420；‎ ‎(2)由题图可知货车的速度为60÷2＝30(千米/小时)，‎ 货车到达A地一共需要2＋360÷30＝14(小时)．‎ 设y2＝kx＋b，代入点(2，0)，(14，360)得 ‎，解得，所以y2＝30x－60；‎ ‎(3)设y1＝mx＋n，代入点(6，0)，(0，360)得 ‎，解得.所以y1＝－60x＋360.‎ 由y1＝y2得30x－60＝－60x＋360，解得x＝.‎ 答：客、货两车经过小时相遇．‎ ‎5. 解：(1)由题图得，甲乙两地相距600千米；‎ ‎(2)由题图得，慢车总用时10小时，‎ ‎∴慢车速度为＝60(千米/小时)，‎ 设快车速度为x千米/小时．‎ 由题图得，60×4＋4x＝600，解得x＝90(千米/小时)，‎ ‎∴快车速度90千米/小时，慢车速度60(千米/小时)；‎ ‎(3)由(2)得，＝(小时)，‎ ‎60×＝400(千米)，时间为小时时快车已到达，此时慢车走了400千米，‎ ‎∴两车相遇后y与x之间的函数关系式为；‎ ‎(4)设出发x小时后，两车相距300千米，‎ ‎①当两车相遇前，由题意得：60x＋90x＝600－300，解得x＝2；‎ ‎②当两车相遇后，由题意得：60x＋90x＝600＋300，解得x＝6，‎ 即两车行驶6小时或2小时后，两车相距300千米．‎ 类型二　方案选取型问题 ‎1. 现代互联网技术的广泛应用，催生了快递行业的高速发展．小明计划给朋友快递一部分物品，经了解有甲、乙两家快递公司比较合适．甲公司表示：快递物品不超过‎1千克的，按每千克22元收费；超过‎1千克，超过的部分按每千克15元收费．乙公司表示：按每千克16元收费，另加包装费3元，设小明快递物品x千克．‎ ‎(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式；‎ ‎(2)小明选择哪家快递公司更省钱？‎ ‎2. (2017焦作模拟)‎ 某会堂举行专场音乐会，出售的门票分为成人票和学生票，已知购买2张成人票和1张学生票共需45元，购买1张成人票和2张学生票共需30元．‎ ‎(1)求成人票和学生票的单价分别是多少？‎ ‎(2)暑假期间，为了丰富广大师生的业余文化生活，该会堂制定了两种优惠方案，方案①：购买一张成人票赠送一张学生票；方案②：按总价的90%付款，某校有4名老师与若干名(不少于4人)学生听音乐会．设学生人数为x(人)，付款总金额为y(元)，分别求出两种优惠方案中y与x的函数关系式；‎ ‎(3)在(2)的条件下，请计算并确定出最节省费用的购票方案．‎ ‎3. 新农村社区改造中，有一部分楼盘要对外销售．某楼盘共23层，销售价格如下：第八层楼房售价为4000元/米2，从第八层起每上升一层，每平方米的售价提高50元；反之，楼层每下降一层，每平方米的售价降低30元．已知该楼盘每套楼房面积均为‎120米2.‎ 若购买者一次性付清所有房款，开发商有两种优惠方案：‎ 方案一：降价8%，另外每套楼房赠送a元装修基金；‎ 方案二：降价10%，没有其他赠送．‎ ‎(1)请写出售价y(元/米2)与楼层x(1≤x≤23，x取整数)之间的函数关系式；‎ ‎(2)老王要购买第十六层的一套楼房，若他一次性付清购房款，请帮他计算哪种优惠方案更加合算．‎ ‎4. 某移动通讯公司开设了两种通讯业务：“全球通”使用者先缴50元月基础费，然后每通话1分钟，再付0.4元；“神州行”不缴月基础费，每通话1分钟，付话费0.6元(这里均指市内通话)．若一个月内通话时间为x分钟，两种通讯方式的费用分别为y1元和y2元．‎ ‎(1)写出y1，y2与x的关系式；‎ ‎(2) 某人估计一个月内通话300分钟，应选择哪种移动通讯合算些．‎ ‎(3)一个月通话为多少分钟时，哪种业务更优惠？‎ ‎5. 为奖励在社会实践活动中表现优异的同学，某校准备购买一批文具袋和水性笔作为奖品．已知文具袋的单价是水性笔单价的5倍，购买5支水性笔和3个文具袋共需60元．‎ ‎(1)求文具袋和水性笔的单价；‎ ‎(2)学校准备购买文具袋20个，水性笔若干支，文具店给出两种优惠方案：‎ A：购买一个文具袋，赠送1支水性笔；‎ B：购买水性笔10支以上，超出10支的部分按原价的八折优惠，文具袋不打折．‎ ‎①设购买水性笔x支，选择方案A总费用为y1元，选择方案B总费用为y2元，分别求出y1，y2与x的函数关系式；‎ ‎②若学校购买水性笔超过10支，选择哪种方案更合算？请说明理由．‎ 参考答案 ‎1. 解：(1)甲快递公司快递该物品的费用y1(元)与x(千克)之间的函数关系式为：‎ 当0＜x≤1时，y1＝22x；‎ 当x>1时，y1＝22＋15(x－1)＝15x＋7.‎ ‎∴y1＝，‎ 乙快递公司快递该物品的费用y2(元)与x(千克)之间的函数关系式为y2＝16x＋3；‎ ‎(2)若0＜x≤1，当22x＞16x＋3时，0，即0.5x－12>0时，解得x>24，‎ 当x>24时，优惠方案②付款较少．‎ ‎3. 解：(1)当1≤x≤8时，每平方米的售价为y＝4000－(8－x)×30＝30x＋3760(元/平方米)；‎ 当9≤x≤23时，每平方米的售价为 y＝4000＋(x－8)×50＝50x＋3600(元/平方米)．‎ ‎∴y＝.‎ ‎(2)第十六层楼房的每平方米的价格为：50×16＋3600＝4400(元/平方米)，‎ 设所交房款为W元．‎ 按照方案一所交房款为：W1＝4400×120×(1－8%)－a＝485760－a(元)，‎ 按照方案二所交房款为：W2＝4400×120×(1－10%)＝475200(元)，‎ 当W1＞W2时，即485760－a＞475200，‎ 解得：0＜a＜10560；‎ 当W1＝W2时，即a＝10560；‎ 当W1＜W2时，即485760－a＜475200，‎ 解得：a＞10560，‎ ‎∴当0＜a＜10560时，方案二合算；当a＝10560元时两种方案一样；当a＞10560时，方案一合算．‎ ‎4. 解：(1)根据题意得：y1＝50＋0.4x；‎ y2＝0.6x.‎ ‎(2)将x＝300代入到y1＝50＋0.4x，得y1＝170，将x＝300代入到y2＝0.6x，得y2＝180.∵170<180，∴选择全球通业务更优惠．‎ ‎(3)当y1>y2时，有50＋0.4x>0.6x，‎ 解得：x<250；‎ 当y1＝y2时，有50＋0.4x＝0.6x，x＝250；‎ 当y1250，‎ 答：当一个月通话时间小于250分钟时，选择“神州行”业务更优惠；当一个月通话时间为250分钟时，选择“全球通”和“神州行”业务费用相同；当一个月通话时间大于250分钟时，选择“全球通”业务更优惠．‎ ‎5. 解：(1)设水性笔的单价是x元，则文具袋的单价是5x元．‎ 由题意得5x＋3×5x＝60，解得x＝3，则5x＝15，所以水性笔的单价是3元，文具袋的单价是15元；‎ ‎(2)①根据题意，得y1＝20×15＋3×(x－20)＝3x＋240，‎ 当0≤x≤10时，y2＝3x＋300；‎ 当x>10时，y2＝20×15＋3×10＋3×0.8(x－10)＝2.4x＋306.‎ ‎②当y1>y2时，可知3x＋240>2.4x＋306，解得x>110，‎ 所以当购买数量超过110支时，选择方案B更合算；‎ 当y1＝y2时，可知3x＋240＝2.4x＋306，解得x＝110，‎ 所以当购买数量为110支时，选择方案A、B均可；‎ 当y10，∴w随x的增大而增大，‎ ‎∴当x＝20时，w有最大值，最大值为5×20＋1770＝1870.‎ ‎∴A款式服装分配给甲、乙两店铺分别为20件和16件，B款式服装分配给甲、乙两店铺分别为10件和14件，王老板获得利润最大，最大的总利润为1870元．‎ ‎3. 解：(1)设第一批次收购x吨蒜薹，则第二批次收购(100－x)吨蒜薹，由题意得，‎ ‎4000x＋1000(100－x)＝160000，解得，x＝20，∴100－x＝80，‎ ‎∴第一批次收购20吨蒜薹，第二批次收购80吨蒜薹；‎ ‎(2)设精加工数量为y吨，则粗加工数量为(100－y)吨，‎ ‎∵精加工数量不多于粗加工数量的3倍，∴y≤3(100－y)，解得y≤75，‎ 设获得的利润为w元，由题意可得w与y之间的关系式为 w＝1000y＋400(100－y)，整理得w＝600y＋40000，‎ ‎∵w是y的一次函数，且k＝600＞0，∴w随y的增大而增大，‎ ‎∴当y取最大值时，w最大，‎ ‎∵y≤75，∴当y＝75时，w最大，最大值w＝600×75＋40000＝85000.‎ 综上所述，精加工数量为75吨时，可获得最大利润，最大利润是85000元．‎ ‎4. 解：(1)设A种足球单价为x元，则B种足球单价为(x＋80)元，‎ 根据题意，得＝2×，解得x＝120，‎ 经检验：x＝120是原分式方程的解．‎ 答：A种足球单价为120元，B种足球单价为200元．‎ ‎(2)设再次购买A种足球x个，则B种足球为(18－x)个．‎ 根据题意，得W＝120x＋200(18－x)＝－80x＋3600，‎ ‎∵18－x≥2x，∴x≤6，∵－80<0，∴W随x的增大而减小，‎ ‎∴当x＝6时，W最小，此时18－x＝12，‎ 答：本次购买A种足球6个，B种足球12个，才能使购买费用W最少．‎ ‎5. 解：(1)设一辆大型渣土运输车每次运土方x吨，一辆小型渣土运输车每次运土方y吨，根据题意，得，解得，‎ 答：一辆大型渣土运输车每次运土方10吨，一辆小型渣土运输车每次运土为5吨；‎ ‎(2)设派出小型渣土运输车m辆，则派出大型渣土运输车为(20－m)辆，根据题意，得，解得7≤m≤10，∵m取整数，∴m＝7，8，9，10.‎ ‎∴有如下四种方案：‎ ‎①派出小型渣土运输车7辆，派出大型渣土运输车为13辆；‎ ‎②派出小型渣土运输车8辆，派出大型渣土运输车为12辆；‎ ‎③派出小型渣土运输车9辆，派出大型渣土运输车为11辆；‎ ‎④派出小型渣土运输车10辆，派出大型渣土运输车为10辆；‎ ‎(3)设总费用为W元，派出小型渣土运输车m辆，则派出大型渣土运输车为(20－m)辆，根据题意得W＝‎300m＋500(20－m)＝－‎200m＋10000，‎ ‎∵k＝－200<0，∴W随m的增大而减小，‎ ‎∴当m＝10时，W最小，最小值为8000元．‎ 故该公司选择方案为小型渣土运输车10辆，大型渣土运输车10辆．‎ ‎6. 解：(1)设用乙、丙两种型号的货轮分别为x艘、y艘，‎ 则，解得，‎ 答：用2艘乙种型号的货轮，6艘丙种型号的货轮；‎ ‎(2)设乙型货轮有n艘，则甲型有20－(m＋n)艘，根据题意得 ‎10[20－(m＋n)]＋5n＋‎7.5m＝180，解得n＝4－‎0.5m，‎ ‎∴20－(m＋n)＝16－‎0.5m，‎ 即甲型货轮有(16－‎0.5m)艘，乙型货轮有(4－‎0.5m)艘，‎ 由题意得4－‎0.5m＋m≤16－‎0.5m，解得m≤12，‎ ‎∵m，16－‎0.5m，4－‎0.5m均为正整数，∴m＝2，4，6，‎ 设集团的总利润为w，‎ 则w＝10×5(16－‎0.5m)＋5×3.6(4－‎0.5m)＋7.5×‎4m＝－‎4m＋872，‎ ‎∵－4<0，∴w随m的增大而减小，‎ 故当m＝2时，w最大，最大值为864，此时利润为864×100×10000＝8.64(亿元)．‎ 此时16－0.5×2＝15，4－0.5×2＝3.‎ 答：甲型货轮有15艘，乙型货轮有3艘，丙型货轮有2艘时，可获得最大利润，最大利润为8.64亿元．‎ ‎7. 解：(1)y＝－2x＋80(20≤x≤28)；‎ ‎【解法提示】设一次函数的表达式为：y＝kx＋b(k≠0)，将点(22，36)、点(24，32)分别代入求得：y＝－2x＋80；‎ ‎(2)由题意知，(x－20)(－2x＋80)＝150，整理得x2－60x＋875＝0，‎ ‎(x－25)(x－35)＝0，解得x1＝25，x2＝35(不合题意，舍去)，‎ 答：每本纪念册的销售单价是25元；‎ ‎(3)由题意知，w＝(x－20)(－2x＋80)＝－2x2＋120x－1600＝－2(x－30)2＋200，‎ ‎∵a＝－2＜0，∴二次函数图象开口向下，‎ ‎∴当x＜30时，w随x的增大而增大，‎ ‎∵20≤x≤28，∴当x＝28时，w最大＝－2×(28－30)2＋200＝192(元)，‎ 答：当纪念册销售单价定为28元时，所获利润最大，最大利润为192元．‎