自贡市2010年中考数学试卷 16页

绝密★启用前 [考试时间：2010年6月12日上午9∶00-11∶00]‎ ‎2010年四川省自贡市初中毕业生学业考试 数 学 试 卷 本试卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分。第Ⅰ卷1至2页，第Ⅱ卷3至14页，满分150分，考试时间为120分钟。考试结束后，将试卷第Ⅰ卷、试卷第Ⅱ卷和答题卡一并交回。装订时将第Ⅱ卷单独装订。‎ 第Ⅰ卷（选择题 共36分）‎ 注意事项：‎ ‎（1）答第Ⅰ卷前，考生务必将自己的姓名，准考号、考试科目涂写在答题卡上。‎ ‎（2）每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其它答案标号，不能答在试卷中。‎ ‎ 一、选择题（本大题共12个小题，每小题3分，共计36分）‎ ‎1．下列各数中，最小的实数是（ ）。‎ A．－ B．－ C．－2 D．‎ ‎2．若式子在实数范围内有意义，则x的取值范围是（ ）。‎ A．x＜－5 B．x＞－‎5 ‎C．x≠－5 D．x≥－5‎ ‎3．数据1，2，x，－1，－2的平均数是0，则这组数据的方差是（ ）。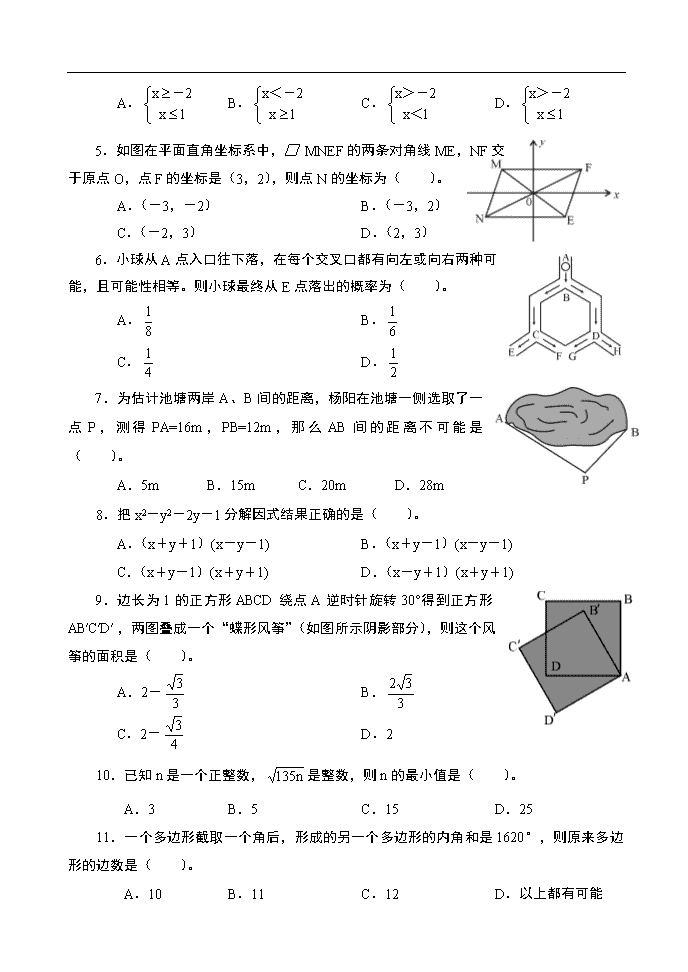‎ A．1 B．‎2 ‎C．3 D．4‎ ‎4． 如图所表示的是下面哪一个不等式组的解集（ ）。‎ A． B． C． D． ‎ ‎5．如图在平面直角坐标系中，□ MNEF的两条对角线ME，NF交 于原点O，点F的坐标是（3，2），则点N的坐标为（ ）。‎ A．（－3，－2） B．（－3，2） ‎ C．（－2，3） D．（2，3）‎ ‎6．小球从A点入口往下落，在每个交叉口都有向左或向右两种可 能，且可能性相等。则小球最终从E点落出的概率为（ ）。‎ A． B． ‎ C． D． ‎ ‎7．为估计池塘两岸A、B间的距离，杨阳在池塘一侧选取了一点P，测得PA=‎16m，PB=‎12m，那么AB间的距离不可能是（ ）。‎ A．‎5m B．‎15m C．‎20m D．‎‎28m ‎8．把x2－y2－2y－1分解因式结果正确的是（ ）。‎ A．（x＋y＋1）(x－y－1) B．（x＋y－1）(x－y－1)‎ C．（x＋y－1）(x＋y＋1) D．（x－y＋1）(x＋y＋1)‎ ‎9．边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB′C′D′，两图叠成一个“蝶形风筝”（如图所示阴影部分），则这个风筝的面积是（ ）。‎ A．2－ B．‎ C．2－ D．2 ‎ ‎10．已知n是一个正整数，是整数，则n的最小值是（ ）。‎ A．3 B．‎5 ‎C．15 D．25‎ ‎11．一个多边形截取一个角后，形成的另一个多边形的内角和是1620°，则原来多边形的边数是（ ）。‎ A．10 B．‎11 ‎C．12 D．以上都有可能 ‎ ‎12．y=x2＋（1－a）x＋1是关于x的二次函数，当x的取值范围是1≤x≤3时，y在x＝1时取得最大值，则实数a的取值范围是（ ）。‎ A．a=5 B．a≥‎5 ‎C．a＝3 D．a≥3 ‎ 绝密★启用前 【考试时间：2010年6月12日上午9：00—11：00】‎ ‎2010年四川省自贡市初中毕业生学业考试 数 学 试 卷 第Ⅱ卷（非选择题 共114分）‎ 注意事项：1．答题前，将密封线内的项目填写清楚。‎ ‎ 2．用蓝色或黑色笔中的一种作答（不能用铅笔），答案直接写在试卷上。‎ 题 号 二 三 四 五 六 总 分 总 分 人 得 分 ‎ 二、填空题（本大题共5个小题，每小题5分，‎ 共计25分）‎ ‎13．关于x的一元二次方程－x2＋（‎2m＋1）x＋1－m2=0无实数根，则m的取值范围是_______________。‎ ‎14．下表是我市今年某天各区县的降雨量分布情况统计（单位：mm）‎ 区县 自井 大安 贡井 沿滩 荣县 富顺 降水量 ‎22‎ ‎23.8‎ ‎19.2‎ ‎23.6‎ ‎20.3‎ ‎23.6‎ 则该组数据的中位数是___________，众数是___________，极差是___________。‎ ‎15．为迎接省运会在我市召开，市里组织了一个梯形鲜花队参加开幕式，要求共站60排，第一排40人，后面每一排都比前一排多站一人，则每排人数y与该排排数x之间的函数关系式为______________________________________________。‎ ‎16．如图，点Q在直线y＝－x上运动，点A的坐标为（1，0），当线段AQ最短时，点Q的坐标为__________________。‎ ‎17．两个反比例子函数y＝，y＝在第一象限内的图象如图所示，点P1，P2，P3，……，P2010在反比例函数y＝图象上，它们的横坐标分别是x1，x2，x3，……，x2010，纵坐标分别是1，3，5，……，共2010个连续奇数，过点P1，P2，P3，……，P2010分别作y轴的平行线，与y＝的图象交点依次是Q1（x1，y1），Q2（x2，y2），Q3（x3，y3），……，Q2010（x2010，y2010），则y2010＝_______________。‎ 三、解答题（本大题共4个小题：每小题6分，共计24分）。‎ ‎18．计算(π－)°＋()－1－cos30°‎ ‎19．解不等式组 ‎20．作出下面立体图形的三视图。‎ ‎21．玉树大地震发生后，小超把本年级同学的捐款情况统计并制成图表，如下 金额（元）‎ 人数 频率 ‎10≤x＜20‎ ‎40‎ ‎0.1‎ ‎20≤x＜30‎ ‎80‎ ‎0.2‎ ‎30≤x＜40‎ m ‎0.4‎ ‎40≤x＜50‎ ‎100‎ n ‎50≤x＜60‎ ‎20‎ ‎0.05‎ 请根据图表提供的信息解答下列问题：‎ ‎（1）表中m和n所表示的数分别是多少？‎ ‎（2）补全频数分布直方图。‎ ‎（3）捐款金额的中位数落在哪个段？‎ 四、解答题：（本大题共3个小题，每小题8分，共计24分）‎ ‎22．如图是一个常见铁夹的侧面示意图，OA，OB表示铁夹的两个面，C是轴，CD⊥OA于点D，已知DA＝‎15mm，DO＝‎24mm，DC＝‎10mm，我们知道铁夹的侧面是轴对称图形，请求出A、B两点间的距离。‎ ‎23．如图：把一张给定大小的长方形卡片ABCD放在宽度为‎10mm的横格纸中，恰好四个顶点都在横格线上，已知α＝32°，求长方形卡片的周长。‎ ‎（参考数据 sin32°≈0.5 cos32°≈0.8 tan32°≈0.6）‎ ‎24．如图，在□ABCD中，BE⊥AD于点E，BF⊥CD于点F，AC与BE、BF分别交于点G，H。‎ ‎（1）求证：△BAE∽△BCF ‎（2）若BG＝BH，求证四边形ABCD是菱形 五、解答题（本大题共2个小题，每小题 ‎9分，共计18分）‎ ‎25．如图，有一直径是‎1米的圆形铁皮，要从中剪出一个圆心角是120°的扇形ABC，求：（1）被剪掉阴影部分的面积。‎ ‎（2）若用所留的扇形铁皮围成一个圆锥，该圆锥底面圆的半径是多少？‎ ‎26．玲玲家准备装修一套新住房，若甲、乙两个装饰公司合作，需6周完成，共需装修费为5.2万元；若甲公司单独做4周后，剩下的由乙公司来做，还需9周才能完成，共需装修费4.8万元。玲玲的爸爸妈妈商量后决定只选一个公司单独完成。‎ ‎（1）如果从节约时间的角度考虑应选哪家公司？‎ ‎（2）如果从节约开支的角度考虑呢？请说明理由。‎ 六、解答题：（本大题共两个小题，27题11分，28题12分，共计23分）‎ ‎27．如图，⊙O是△ABC的外接圆，∠A＝30°，AB是⊙O的直径，过点C作⊙O的切线，交AB延长线于D，CD＝‎3‎cm，‎ ‎（1）求⊙O的直径。‎ ‎（2）若动点M以‎3cm/s的速度从点A出发沿AB方向运动。同时点N以‎1.5cm/s的速度从B点出发沿BC方向运动。设运动的时间为t(0≤t≤2)，连结MN，当t为何值时△BMN为Rt△？并求此时该三角形的面积？‎ ‎28．如图，在直角坐标平面内，O为坐标原点，A点的坐标为（1，0），B点在x轴上且在点A的右侧，AB＝OA，过点A和B作x轴的垂线分别交二次函数y＝x2的图象于点C和D，直线OC交BD于M，直线CD交y轴于点H。记C、D的横坐标分别为xC，xD，点H的纵坐标 yH。‎ ‎（1）证明：①S△CMD∶S梯形ABMC＝2∶3‎ ‎②xC·xD＝－yH ‎（2）若将上述A点坐标（1，0）改为A点坐标（t，0），t＞0，其他条件不变，结论S△CMD：S梯形ABMC＝2∶3是否仍成立？请说明理由。‎ ‎（3）若A的坐标（t，0）（t＞0），又将条件y＝x2改为y＝ax2（a＞0），其他条件不变，那么XC、XD和yH又有怎样的数量关系？写出关系式，并证明。‎ 绝密★启用前 [考试时间：2010年6月12日上午9∶00-11∶00]‎ ‎2010年四川省自贡市初中毕业生学业考试 数学参考答案及评分标准 第Ⅰ卷（选择题 共36分）‎ 一、选择题：（每小题3分，共36分）‎ ‎1．C 2．D 3．B 4．D 5．A ‎ ‎6．C 7．D 8．A 9．A 10．C ‎11．D 12．B 绝密★启用前 ‎2010年四川省自贡市初中毕业生学业考试 数学参考答案及评分标准 第Ⅱ卷（非选择题 共114分）‎ 说明：‎ 一、如果考生的解法与下面提供的参考解法不同，只要正确一律给满分，若某一步出现错误，可参照该题的评分意见进行评分。‎ 二、评阅试卷时，不要因解答中出现错误而中断对该题的评阅，当解答中某一步出现错误，影响了后继部分，但该步以后的解答未改变这一道题的内容和难度，后来发生第二次错误前，出现错误的那一步不给分，后面部分只给应给分数之半；明显笔误，可酌情少扣；如有严重概念性错误，则不给分；在同一解答中，对发生第二次错误起的部分不给分。‎ 三、涉及计算过程，允许合理省略非关键性步骤。‎ 四、在几何题中，考生若使用符号“”进行推理，其每一步应得分数，可参照该题的评分意见进行评分。‎ 二、填空题：（每小题5分，共计25分）‎ ‎13．m＜－‎ ‎14．22.8 23.6 4.6‎ ‎15．y＝39＋x （x＝1，2，……，60）‎ ‎16．（，－）‎ ‎17．2009.5‎ 三、解答题：（每小题6分，共计24分）‎ ‎18．解：原式＝1＋3－3· ……………………………………………………（4＇）‎ ‎＝4－ ……………………………………………………………………（5＇）‎ ‎ ＝－ ……………………………………………………………………（6＇）‎ ‎19．解：由①得x＞5 ……………………………………………………………………（2＇）‎ 由②得x≤－4 ……………………………………………………………………（4＇）‎ ‎∴原不等式组无解 ……………………………………………………………………（6＇）‎ ‎20．‎ 主视图…………………………………（1＇）‎ 俯视图…………………………………（1＇）‎ 左视图…………………………………（1＇）‎ 位置-------------（1＇） 内外比例----------（各1分共2＇）‎ ‎21．（1）m＝160，n＝0.25 ………………………………………………………………（2＇）‎ ‎（2）如图 ‎…………………………………………（4＇）‎ ‎（3）捐款金额的中位数落在30元～40元这个金额段 …………………………………（6＇）‎ 四、解答题：（每小题8分，共计24分）‎ ‎22．解：作出示意图 ‎ ‎ 连接AB，同时连结OC并延长交AB于E， …………………………………………（1＇）‎ 因为夹子是轴对称图形，故OE是对称轴 ……………………………………………（2＇）‎ ‎∴OE⊥AB AE＝BE …………………………………………………………（3＇）‎ ‎∴Rt△OCD∽Rt△OAE ………………………………………………………………（4＇）‎ ‎∴＝ ……………………………………………………………………………（5＇）‎ 而OC＝＝＝26 ………………………………………………（6＇）‎ 即＝ ∴AE＝＝15 ………………………………（7＇）‎ ‎∴AB＝2AE＝30（mm） …………………………………………………………（8＇）‎ 答：AB两点间的距离为30mm.‎ ‎23．解：作AF⊥l4，交l2于E，交l4于F ………………………………………………（1＇）‎ 则△ABE和△AFD均为直角三角形 …………………………………………（2＇）‎ 在Rt△ABE中，∠ABE＝∠α＝32°‎ sin∠ABE＝ ………………………………………………………………（3＇）‎ ‎∴AB＝＝＝40 ……………………………………………………（4＇）‎ ‎∵∠FAD＝90°－∠BAE ∠α＝90°－∠BAE ‎∴∠FAD＝∠α＝32° … ………………………………………………………（5＇）‎ 在Rt△AFD中， cos∠FAD＝ ……………………………………（6＇）‎ AD＝＝＝50 ……………………………………………………（7＇）‎ ‎∴长方形卡片ABCD的周长为（40＋50）×2＝180（mm） ……………（8＇）‎ ‎24．证明（1）∵BE⊥AD，BF⊥CD ‎∴∠BEA＝∠BFC＝90° ………………（1＇）‎ 又ABCD是平行四边形，‎ ‎∴∠BAE＝∠BCF ……………………（2＇）‎ ‎∴△BAE∽△BCF ……………………………………………………（3＇）‎ ‎（2）∵△BAE∽△BCF ‎ ∴∠1＝∠2 ………………………………………………………………（4＇）‎ 又BG＝BH ∴∠3＝∠4‎ ‎∴∠BGA＝∠BHC ……………………………………………………（5＇）‎ ‎∴△BGA≌△BHC（ASA） …………………………………………（6＇）‎ ‎∴AB＝BC ………………………………………………………………‎ ‎（7＇）‎ ‎∴□ABCD为菱形 ……………………………………………………（8＇）‎ 五、解答题：（每小题9分，共计18分）‎ ‎25．解：（1）设O为圆心，连OA、OB …………（1＇）‎ ‎∵OA＝OC＝OB AB＝AC ‎∴△ABO≌△ACO （sss） 又∠BAC＝120°‎ ‎∴∠BAO＝∠CAO＝60°‎ ‎∴△ABO是等边三角形 ‎∴AB＝ … ……………………………………………………………（3＇）‎ ‎∴S扇形ABC＝π（）2‎ ‎ ＝ ……………………………………………………………（5＇）‎ ‎∴S阴影＝π ()2－‎ ‎＝ ………………………………………………………………（6＇）‎ ‎（2）在扇形ABC中，的长为·＝ ………………………………（7＇）‎ 设底面圆的半径为r。‎ 则 2πr＝ ………………………………………………………………（8＇）‎ ‎∴r＝ … ……………………………………………………………（9＇）‎ ‎26．解：（1）设甲公司的工作效率为m，乙公司的工作效率为n ……………………（1＇）‎ 则 …………（2＇） 解得 ……………（3＇）‎ 故从节约时间的角度考虑应选择甲公司 ………………………………（4＇）‎ ‎（2）由（1）知甲、乙完成这次工程分别需10周、15周 ………………（4.5＇）‎ 设需付甲公司每周装修费x万元，乙公司y万元 …………………………（5＇）‎ 则 …………（6＇） 解得 ……………（7＇）‎ 此时 …………………………………………………………（8＇）‎ 故从节约开支的角度出发应选择乙公司 ……………………………………（9＇）‎ 六、解答题：（本大题共两个小题，27题11分，28题12分，共计23分）‎ ‎27．（1）解：∵AB是⊙O的直径.‎ ‎∴∠ACB＝90° ………………………（0.5＇）‎ 又∠A＝30°‎ ‎∴∠ABC＝60° …………………………（1＇）‎ 连接OC，因CD切⊙O于C，则∠OCD＝90° ……………………（2＇）‎ 在△OBC中 ‎∵OB＝OC，∠ABC＝60°‎ ‎∴∠OCB＝60°‎ ‎∴∠BCD＝30° ……………………………………………………（2.5＇）‎ 又∠OBC＝∠BCD＋∠D ‎∴∠D＝30° …………………………………………………………（3＇）‎ ‎∴AC＝CD＝3 ……………………………………………………（3.5＇）‎ 在Rt△ABC中，cosA＝‎ ‎∴AB＝＝＝6（cm） ……………………………………（5＇）‎ ‎（2）△BMN中，①当∠BNM＝90°时，cos∠MBC＝‎ 即cos60°＝ ∴t＝1 ………………………（6＇）‎ 此时BM＝3 BN＝1.5 MN＝＝ …………（7＇）‎ ‎∴S△BMN＝BN·MN＝ （cm2） ………………………（8＇）‎ ‎②当∠NMB＝90°时，cos∠MBC＝‎ 即cos60°＝ ∴ t＝1.6 ………………………………………（9＇）‎ 此时BM＝ BN＝ MN＝＝ ………（10＇）‎ ‎∴S△BMN＝ BM·MN＝××＝（cm2） ………………（11＇）‎ ‎28．解：（1）由已知可得点B的坐标为（2，0）点C的坐标为（1，1），点D的坐标为（2，4），且直线OC的函数解析式为y＝x。‎ ‎∴点M的坐标为（2，2），易得S△CMD＝1，S梯形ABMC＝ ………………（1.5＇）‎ ‎∴S△CMD∶S梯形ABMC＝2∶3，即结论①成立。‎ 设直线CD的函数解析式为y＝kx＋b，则 ‎ 即 ‎ ‎∴直线CD的解析式为y＝3x－2。‎ 由上述可得点H的坐标为（0，－2），即yH＝－2 ………………………（2.5＇）‎ ‎∴xC·xD＝－yH. 即结论②成立 ………………………………………………（3＇）‎ ‎（2）结论S△CMD：S梯形ABMC＝2:3仍成立. ……………………………………………（4＇）‎ 理由如下：∵点A的坐标为（t，0），（t＞0）.‎ 则点B的坐标为（2t，0）‎ 从而点C的坐标为（t，t2），点D的坐标为（2t，4t2）.‎ 设直线OC的解析式为y＝kx，则t2＝kt 得k＝t ‎∴直线OC的解析式为y＝tx ……………………………………（5＇）‎ 又设M的坐标为（2t，y）‎ ‎∵点M在直线OC上 ‎∴当x＝2t时，y＝2t2‎ ‎∴点M的坐标为（2t，2t2） ……………………………………（6＇）‎ ‎∴S△CMD：S梯形ABMC＝·2t2·t∶（t2＋2t2）·t ‎ ＝t3∶（t3）‎ ‎＝ …………………………………………（7＇）‎ ‎（3）xC，xD和yH有关数量关系xC·xD＝－yH. …………………………………（8＇）‎ 由题意，当二次函数的解析式为y＝ax2（a＞0），且点A的坐标为（t，0）时，点C的坐标为（t，at2），点D的坐标为（2t，4at2） …………………………（9＇）‎ 设直线CD的解析式为y＝kx＋b 则 得 ‎∴CD的解析式为y＝3atx－2at2 ………………………………………………（11＇）‎ 则H的坐标为（0，－2at2）即yH＝－2at2 …………………………………（11.5＇）‎ ‎∵xC·xD＝t·2t＝2t2 ………………………………………… …………………（12＇）‎ ‎∴xC·xD＝－yH.‎