中考数学复习考点跟踪训练42方案设计型问题 7页

考点跟踪训练42方案设计型问题 一、选择题 ‎1．一宾馆有双人间、三人间、四人间三种客房供游客租住，某旅行团20人准备同时租用这三种客房共7间(每种房间至少有一间)，如果每个房间都住满，租房方案有(　　)‎ A．4种B．3种C．2种D．1种 答案A 解析分类讨论：二人间、三人间、四人间分别为(1,2,2)、(2,1,4)、，有2种租房方案．X ‎2．(2010·乌鲁木齐)有若干张面积分别为a2、b2、ab的正方形和长方形纸片，阳阳从中抽取了1张面积为a2的正方形纸片，4张面积为ab的长方形纸片，若他想拼成一个大正方形，则还需要抽取面积为b2的正方形纸片(　　)‎ A．2张B．4张C．6张D．8张 答案B 解析要想拼成一个大正方形，即所用的正方形纸片与长方形纸片的面积需构成一个正方形，由完全平方公式，a2＋4ab＋4b2＝(a＋2b)2，还需4张面积为b2的正方形．‎ ‎3．在平面直角坐标系中，点A的坐标为(1,1)，点B的坐标为(11,1)，点C到直线AB的距离为4，且△ABC是直角三角形，则满足条件的点C有(　　)‎ A．4个B．6个C．8个D．10个 答案C 解析根据A、B两点的坐标，可知直线AB∥x轴，则到直线AB的距离为4的点在平行于直线AB的直线上且距离为4，有两条直线，根据直角三角形斜边上的中线等于斜边的一半，以AB的中点为圆心，5为半径画弧与两直线的交点即为直角三角形的第三个顶点；‎ 若AB是直角边，则满足条件的有4个点(1,5)、(1，－3)、(11,5)、(11，－3)；若AB是斜边，设C(x,5)，过C作AB边上的高，由射影定理得，42＝(x－1)(11－x)，解得x1＝3，x2＝9，所以有(3,5)、(9,5)，根据对称性，得另外两点(3，－3)、(9，－3)．所以共有8个点符合要求．‎ ‎4．一次比赛期间，体育场馆要对观众进行安全检查．设某体育馆在安检开始时已有若干名观众在馆外等候安检，安检开始后，到达体育馆的观众人数按固定速度增加．又设各安检人员的安检效率相同．若用3名工作人员进行安检，需要25分钟才能将等候在馆外的观众检测完，使后来者能随到随检；若用6名工作人员进行安检，时间则缩短为10分钟．现要求不超过5分钟完成上述过程，则至少要安排多少名工作人员进行安检(　　)‎ A.9B．10C．11D．12‎ 答案C 解析假设开始时已有m人等候安检，设工作人员每分钟检测x人，观众每分钟增加y人，至少安排z名工作人员安检，则 ‎①－②，得15x＝15y，x＝y，把x＝y代入②，有60x＝m＋10x，m＝50x.‎ ‎∴zx·5≥50x＋5x,5xz≥55x，z≥11.‎ ‎∴至少要按排11名工作人员进行安检．‎ 二、解答题 ‎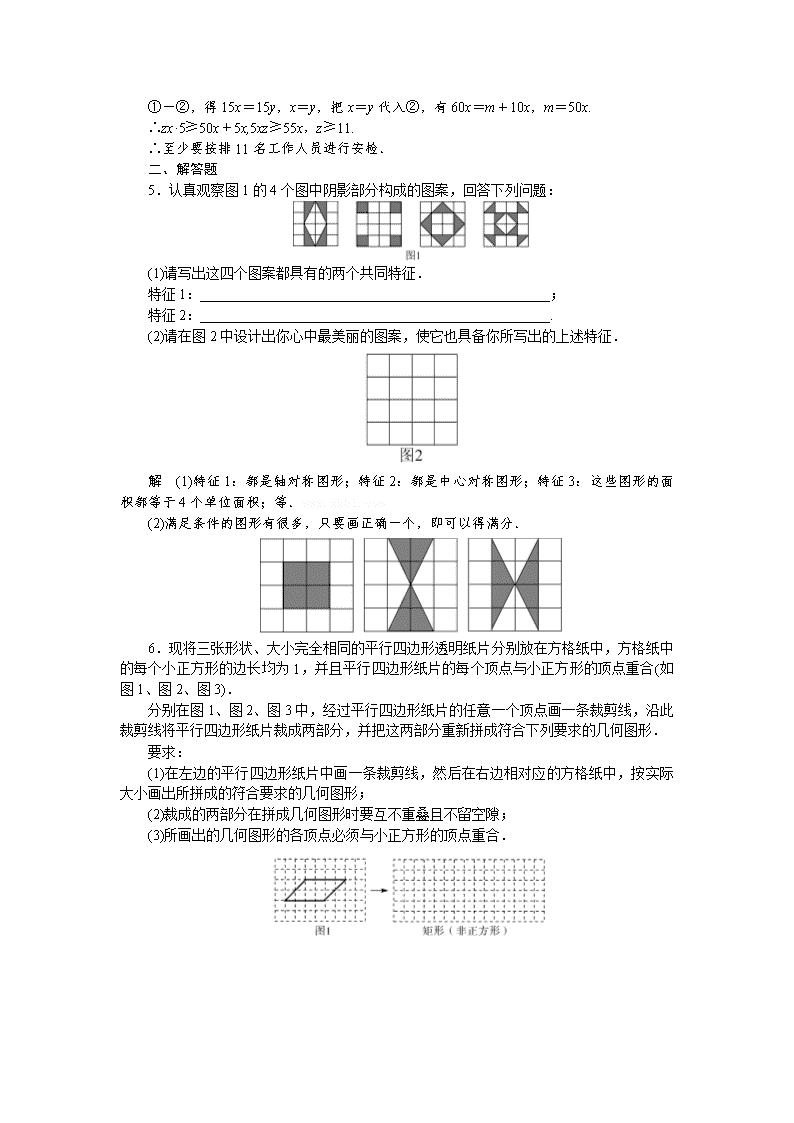5．认真观察图1的4个图中阴影部分构成的图案，回答下列问题：‎ ‎(1)请写出这四个图案都具有的两个共同特征．‎ 特征1：__________________________________________________；‎ 特征2：__________________________________________________.‎ ‎(2)请在图2中设计出你心中最美丽的图案，使它也具备你所写出的上述特征．‎ 解　(1)特征1：都是轴对称图形；特征2：都是中心对称图形；特征3：这些图形的面积都等于4个单位面积；等．www.xkb1.com ‎(2)满足条件的图形有很多，只要画正确一个，即可以得满分．‎ ‎6．现将三张形状、大小完全相同的平行四边形透明纸片分别放在方格纸中，方格纸中的每个小正方形的边长均为1，并且平行四边形纸片的每个顶点与小正方形的顶点重合(如图1、图2、图3)．‎ 分别在图1、图2、图3中，经过平行四边形纸片的任意一个顶点画一条裁剪线，沿此裁剪线将平行四边形纸片裁成两部分，并把这两部分重新拼成符合下列要求的几何图形．‎ 要求：‎ ‎(1)在左边的平行四边形纸片中画一条裁剪线，然后在右边相对应的方格纸中，按实际大小画出所拼成的符合要求的几何图形；‎ ‎(2)裁成的两部分在拼成几何图形时要互不重叠且不留空隙；‎ ‎(3)所画出的几何图形的各顶点必须与小正方形的顶点重合．‎ 解 ‎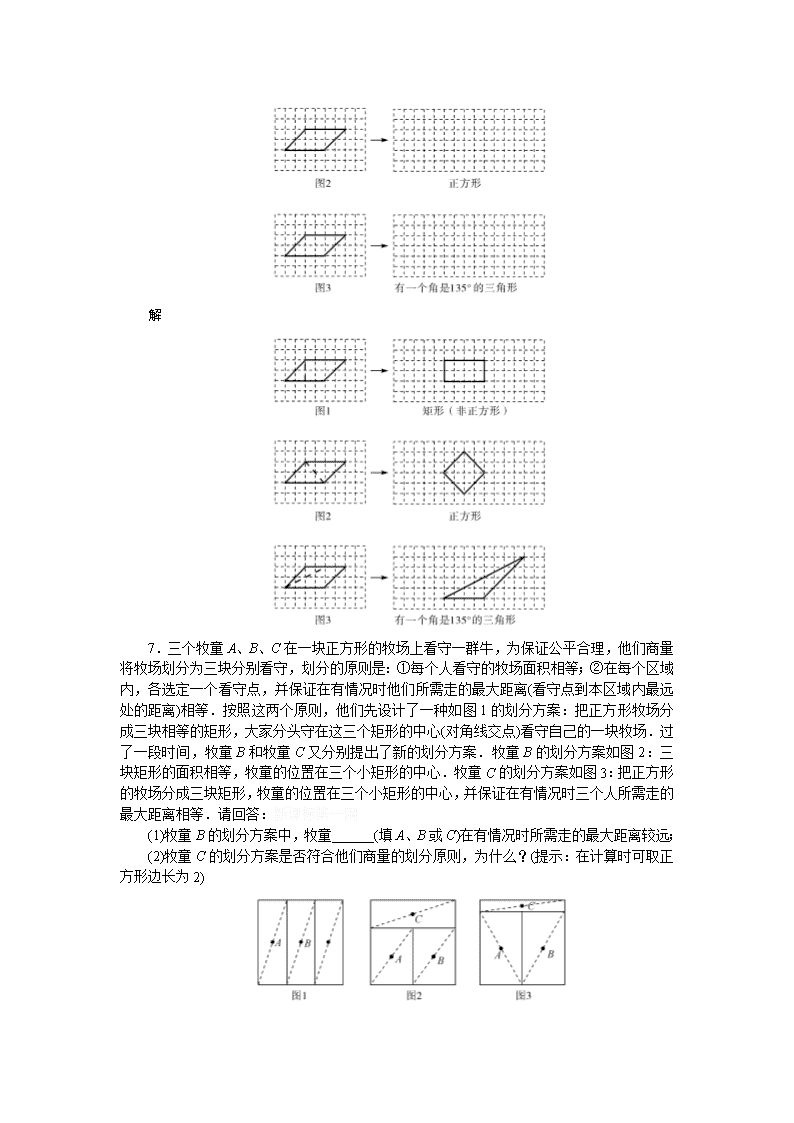7．三个牧童A、B、C在一块正方形的牧场上看守一群牛，为保证公平合理，他们商量将牧场划分为三块分别看守，划分的原则是：①每个人看守的牧场面积相等；②在每个区域内，各选定一个看守点，并保证在有情况时他们所需走的最大距离(看守点到本区域内最远处的距离)相等．按照这两个原则，他们先设计了一种如图1的划分方案：把正方形牧场分成三块相等的矩形，大家分头守在这三个矩形的中心(对角线交点)看守自己的一块牧场．过了一段时间，牧童B和牧童C又分别提出了新的划分方案．牧童B的划分方案如图2：三块矩形的面积相等，牧童的位置在三个小矩形的中心．牧童C的划分方案如图3：把正方形的牧场分成三块矩形，牧童的位置在三个小矩形的中心，并保证在有情况时三个人所需走的最大距离相等．请回答：新课标第一网 ‎(1)牧童B的划分方案中，牧童______(填A、B或C)在有情况时所需走的最大距离较远；‎ ‎(2)牧童C的划分方案是否符合他们商量的划分原则，为什么？(提示：在计算时可取正方形边长为2)‎ 解　(1)C；‎ 易得A、B的距离相等，设正方形的边长为1，他们到最远处的距离为这个直角三角形斜边的一半，根据勾股定理进行计算可得C的距离最大．‎ ‎(2)分别计算A、C的面积，比较它们是否相等再作出判断．‎ 牧童C的划分方案不符合他们商量的划分原则．‎ 理由如下：如图，在正方形DEFG中，四边形HENM、MNFP、DHPG都是矩形，且HN＝NP＝HG.‎ 可知EN＝NF，S矩形HENM＝S矩形MNFP.‎ 取正方形边长为2，设HD＝x，则HE＝2－x.‎ 在Rt△HEN和Rt△DHG中，‎ 由HN＝HG得：EH2＋EN2＝DH2＋DG2.‎ 即：(2－x)2＋12＝x2＋22.‎ 解得：x＝.‎ ‎∴HE＝2－＝.‎ ‎∴S矩形HENM＝S矩形MNFP＝1×＝，‎ S矩形DHPG＝2×＝.‎ ‎∴S矩形HENM≠S矩形DHPG.‎ ‎∴牧童C的划分方案不符合他们商量的划分原则．‎ ‎8．如图，Rt△ABC中，∠ACB＝90°，∠CAB＝30°，用圆规和直尺作图，用两种方法把它分成两个三角形，且要求其中一个三角形是等腰三角形．(保留作图痕迹，不要求写作和证明)‎ 解作法一：作AB边上的中线；‎ 作法二：作∠CBA的平分线；‎ 作法三：在CA上取一点D，使CD＝CB.‎ ‎9．某一广场进行装修，所用三种板材(a＝0.5×0.5，b＝0.2×0.5，c＝0.2×0.2)规格如图所示(单位：米)．‎ ‎(1)根据铺设部分面积的不同大小，设计如下列图案1、2、3有一定规律的图案；中间部分由a种板材铺成正方形，四周由b种和c种板材镶边．‎ ‎①请直接写出图案2的面积；‎ ‎②若某一图案的面积为11.56m2，求该图案每边有b种板材多少块？‎ ‎(2)在第(1)题②所求图案的基础上，根据实际需要，中间由a种板材铺成的部分要设计成长方形，四周仍由b和c种板材镶边，要求原有的三种板材不能浪费，如果需多用材料，只能用b种板材不超过6块，请求出其余的铺设方案．‎ 解　(1)①1.96m2.‎ ‎②设每边有b种板x块，依题意得：‎ ‎(0.5x＋0.2×2)2＝11.56，‎ 整理为：0.5x＋0.4＝±3.4，‎ 解得：x1＝6，x2＝－7.6(舍去)．‎ ‎∴x＝6.‎ ‎∴该图案每边有b种板材6块．‎ ‎(2)依题意，中间部分的a板材共有36块，‎ ‎36＝36×1＝18×2＝12×3＝9×4＝6×6.‎ i)b种板材共需(36＋1)×2＝74块；‎ ii)b种板材共需(18＋2)×2＝40块；‎ iii)b种板材共需(12＋3)×2＝30块；‎ iv)b种板材共需(9＋4)×2＝26块．‎ 依题意，b种板材最多可用6×4＋6＝30块．‎ ‎∴符合条件的其余的铺设方案有2种．‎ ‎10．(2011·广安)广安市某楼盘准备以每平方米6000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米4860元的均价开盘销售．‎ ‎(1)求平均每次下调的百分率；‎ ‎(2)某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，一次性送装修费每平方米80元，试问哪种方案更优惠？‎ 解　(1)设平均每次下调的百分率x，则 ‎6000(1－x)2＝4860，‎ 解得：x1＝0.1，x2＝1.9(舍去)．‎ ‎∴平均每次下调的百分率为10%.‎ ‎(2)方案①可优惠：4860×100×(1－0.98)＝9720(元)．‎ 方案②可优惠：100×80＝8000(元)．‎ ‎∴方案①更优惠．‎ ‎11．(2011·綦江)为了保护环境，某化工厂一期工程完成后购买了3台甲型和2台乙型污水处理设备，共花费资金54万元，‎ 且每台乙型设备的价格是每台甲型设备价格的75%.实际运行中发现，每台甲型设备每月能处理污水200吨，每台乙型设备每月能处理污水160吨，且每年用于每台甲型设备的各种维护费和电费为1万元，每年用于每台乙型设备的各种维护费和电费为1.5万元．今年该厂二期工程即将完成，产生的污水将大大增加，于是该厂决定再购买甲、乙两型设备共8台用于二期工程的污水处理，预算本次购买资金不超过84万元，预计二期工程完成后每月将产生不少于1300吨污水．‎ ‎(1)请你计算每台甲型设备和每台乙型设备的价格各是多少元？‎ ‎(2)请你求出用于二期工程的污水处理设备的所有购买方案；‎ ‎(3)若两种设备的使用年限都为10年，请你说明在(2)的所有方案中，哪种购买方案的总费用最少？(总费用＝设备购买费＋各种维护费和电费)‎ 解　(1)设一台甲型设备的价格为x万元，由题3x＋2×75%x＝54，解得x＝12, 12×75%＝9.‎ ‎∴一台甲型设备的价格为12万元，一台乙型设备的价格为9万元．‎ ‎(2)设二期工程中，购买甲型设备a台，由题意有解得：≤a≤4.‎ 由题意a为正整数，∴a＝1,2,3,4.‎ ‎∴所有购买方案有四种，分别为：‎ 方案一：甲型1台，乙型7台；‎ 方案二：甲型2台，乙型6台；‎ 方案三：甲型3台，乙型5台；‎ 方案四：甲型4台，乙型4台．‎ ‎(3)设二期工程10年用于治理污水的总费用为W万元，‎ W＝12a＋9(8－a)＋1×10a＋1.5×10(8－a)，‎ 化简得：W＝－2a＋192，‎ ‎∵W随a的增大而减少，‎ ‎∴当a＝4时，W最小(逐一验算也可)．‎ ‎∴按方案四，甲型购买4台，乙型购买4台的总费用最少．‎ ‎12．(2011·荆州)2011年长江中下游地区发生了特大旱情，为抗旱保丰收，某地政府制定了农户投资购买抗旱设备的补贴办法，其中购买Ⅰ型、Ⅱ型抗旱设备所投资的金额与政府补贴的额度存在下表所示的函数对应关系.‎ 型号 金额 Ⅰ型设备 Ⅱ型设备 投资金额x(万元)‎ x ‎5‎ x ‎2‎ ‎4‎ 补贴金额y(万元)‎ y1＝kx ‎(k≠0)‎ ‎2‎ y2＝ax2＋bx ‎(a≠0)‎ ‎2.4‎ ‎3.2‎ ‎(1)分别求出y1和y2的函数解析式；‎ ‎(2)有一农户同时对Ⅰ型、Ⅱ型两种设备共投资10万元购买，请你设计一个能获得最大补贴金额的方案，并求出按此方案能获得的最大补贴金额．‎ 解　(1)由题意得：①5k＝2，k＝，∴y1＝x.‎ ‎②解之，得： ‎∴y2＝－x2＋x.‎ ‎(2)设购Ⅱ型设备投资t万元，购Ⅰ型设备投资(10－t)万元，共获补贴Q万元．‎ ‎∴y1＝(10－t)＝4－t，y2＝－t2＋t，‎ Q＝y1＋y2＝4－t－t2＋t＝－(t－3)2＋.‎ ‎∴当t＝3时，Q有最大值为，此时10－t＝7(万元)．‎ 即投资7万元购Ⅰ型设备，投资3万元购Ⅱ型设备，共获最大补贴5.8万元．‎