江苏省无锡市华仕初中中考数学模拟月考试试题 人教新课标 12页

九年级数学中考模拟试卷 注意事项： 1．本卷满分130分．考试时间为120分钟．‎ ‎2．卷中除要求近似计算的结果取近似值外，其余各题均应给出精确结果．‎ 一、选择题（本大题共10题，每小题3分，共计30分．）‎ ‎1．9的平方根等于 （ ▲ ）‎ ‎ A．3 B． C． D．‎ ‎2．下列运算正确的是 （▲ ）‎ ‎ A．a+a=‎2a2 B．a2·a=‎2a2 C．（-ab）2=2ab2 D．（‎2a）2 ÷a=‎‎4a ‎3．使有意义的的取值范围是 （ ▲ ）‎ A． B． C． D．‎ ‎4.下列图形中，中心对称图形有 （ ▲ ） ‎ ‎ ‎ A．1个 B．2个 C．3个 D．4个 ‎5.已知⊙O1与⊙O2相切，⊙O1的半径为‎3cm，⊙O2的半径为‎2cm，则O1O2的长是（▲） ‎ A．‎1 cm B．‎5 cm C．‎1 cm或‎5 cm D．‎0.5cm或‎2.5cm ‎6．小丽在清点本班为青海玉树地震灾区的捐款时发现，全班同学捐款的钞票情况如下：l00元的5 张，50元的l0张，l0元的20张，5元的l0张．在这些不同面额的钞票中，众数是（▲）元的钞票． ‎ ‎ A．5 B．‎10 C．20 D．100‎ ‎7．如图是由几个小立方块所搭成的几何体的俯视图，小正方形中的数字表示在该位置小立方块的个数，则这个几何体的左视图为 （ ▲ ）‎ ‎ ‎ ‎1‎ ‎3‎ ‎2‎ ‎1‎ A．‎ B．‎ C．‎ D．‎ ‎8．下列命题正确的是（ ▲ ）‎ A．两个等边三角形全等 ‎ B．各有一个角是40°的两个等腰三角形全等 C．对角线互相垂直平分的四边形是菱形 ‎ D．对角线互相垂直且相等的四边形是正方形 ‎9．如图a是长方形纸带，，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的的度数是 （▲ ）‎ 图a 图b 图c A．110° B．120° C．140° D．150°‎ 第10题 ‎10.如图，A、B是第二象限内双曲线上的点， A、B两点的横坐标分别是a、‎2a，线段AB的延长线交x轴于点C，若S△AOC=6．则k的值为 （ ▲ ）．‎ ‎ A 6 B. ‎-6 C. 4 D. -4‎ 二、填空题（本大题共8小题，每小题2分，共计16分．）‎ ‎11．9的相反数是 ▲ ．‎ ‎12．上海世博会主题馆屋面太阳能板面积达3万多平方米，年发电量可达280万度.这里 的280万度用科学记数法表示（保留三个有效数字）为___▲_____________度. ‎ 第17题 ‎13．分解因式：a2b－b3＝ ▲ ．‎ ‎14．方程的解是 ▲ ．‎ ‎15．八边形的外角和等于 ▲ °．‎ ‎16．若圆锥的底面半径为‎3cm，高为‎4cm，则这个圆锥的侧面积为 ▲ cm2．‎ ‎17． 如图，△ABC内接于⊙O，AC是⊙O的直径，∠ACB＝500，‎ 点D是 上一点，则∠D＝____▲ ____‎ ‎ ‎ ‎18．如图，在平面直角坐标系上有个点P(1，0)，点P第1次向上跳动1个单位至点P1(1，1)，紧接着第2次向左跳动2个单位至点P2(―1，1)，第3次向上跳动1个单位，第4次向右跳动3个单位，第5次又向上跳动1个单位，第6次向左跳动4个单位，……，依此规律跳动下去，点P第100次跳动至点P100的坐标是 。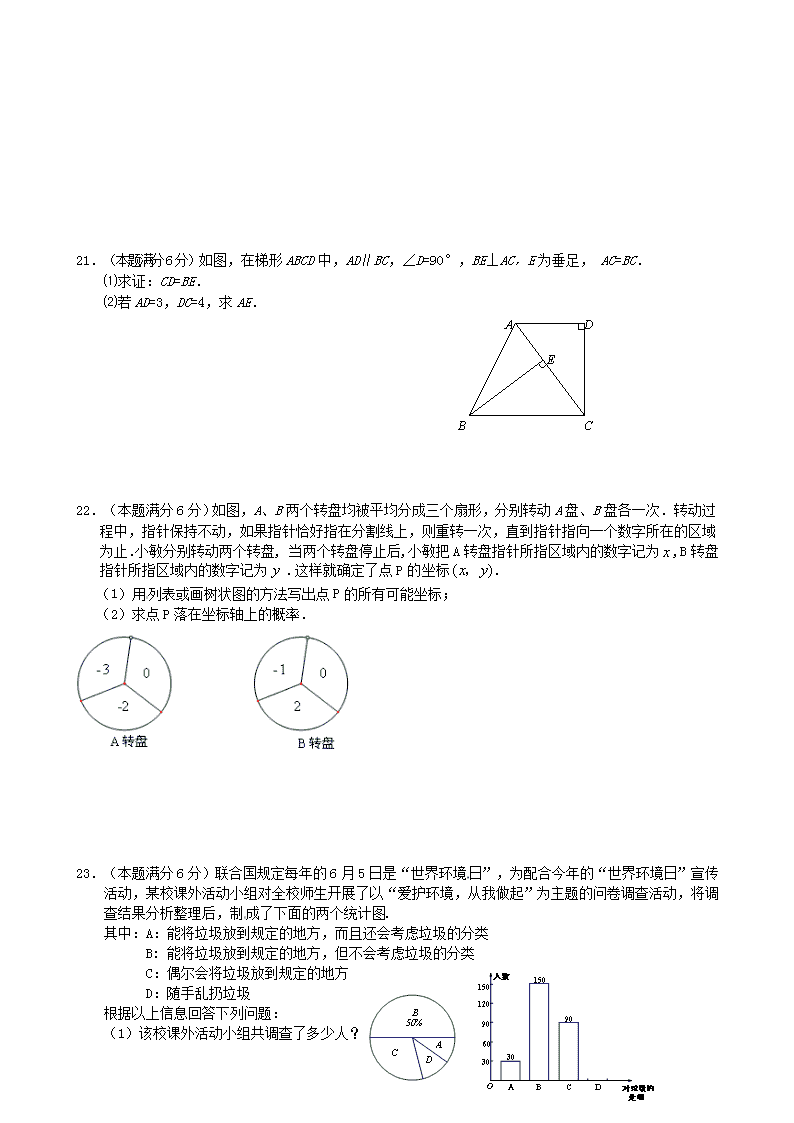‎ 三、解答题（本大题共10小题，共计84分．）‎ ‎19．（本题满分8分）计算：‎ ‎（1） （2‎ ‎20．（本题满分8分）‎ ‎（1）解方程： （2）解不等式组：把解集在数轴上表示出来.‎ ‎21．（本题满分6分）如图，在梯形ABCD中，AD∥BC，∠D=90°，BE⊥AC，E为垂足， AC=BC．‎ ‎ ⑴求证：CD=BE．‎ ‎⑵若AD=3，DC=4，求AE． ‎ A D C B E ‎22．（本题满分6分）如图，A、B两个转盘均被平均分成三个扇形，分别转动A盘、B盘各一次．转动过程中，指针保持不动，如果指针恰好指在分割线上，则重转一次，直到指针指向一个数字所在的区域为止．小敏分别转动两个转盘, 当两个转盘停止后,小敏把A转盘指针所指区域内的数字记为,B转盘指针所指区域内的数字记为.这样就确定了点P的坐标.‎ ‎（1）用列表或画树状图的方法写出点P的所有可能坐标；‎ ‎（2）求点P落在坐标轴上的概率．‎ ‎23．（本题满分6分）联合国规定每年的‎6月5日是“世界环境日”，为配合今年的“世界环境日”宣传活动，某校课外活动小组对全校师生开展了以“爱护环境，从我做起”为主题的问卷调查活动，将调查结果分析整理后，制成了下面的两个统计图.‎ 其中：A：能将垃圾放到规定的地方，而且还会考虑垃圾的分类 ‎ ‎ B: 能将垃圾放到规定的地方，但不会考虑垃圾的分类 ‎ C：偶尔会将垃圾放到规定的地方 ‎ D：随手乱扔垃圾 根据以上信息回答下列问题：‎ ‎（1）该校课外活动小组共调查了多少人？‎ 并补全下面的条形统计图；‎ ‎（2）如果该校共有师生2400人，‎ 那么随手乱扔垃圾的约有多少人？‎ ‎24．（本题满分7分）如图所示，山坡上有一棵与水平面垂直的大树，一场台风过后，大树被刮倾斜后折断倒在山坡上，树的顶部恰好接触到坡面．已知山坡的坡角，量得树干倾斜角，大树被折断部分和坡面所成 的角．‎ ‎（1）求的度数；‎ ‎（2）求这棵大树折断前的高度？‎ ‎（结果精确到个位，参考数据：，，）．‎ C ‎60°‎ ‎38°‎ B D E ‎23°‎ A F ‎25．（本题满分9分）学校选修课上木工制作小组决定制作等腰三角形积木，现从某家具厂找来如图所示的梯形边角余料（单位：cm）．且制作方案如下：‎ ‎（1）三角形中至少有一边长为‎10 cm；‎ ‎（2）三角形中至少有一边上的高为‎8 cm 请你画出三种不同的分割线，并求出相应图形面积．（要求画出的三个等腰三角形的面积不等）‎ ‎26．（本小题满分10分）‎ 如图，在平面直角坐标系中，顶点为（，）的抛物线交轴于点，交轴于，两点（点在点的左侧）， 已知点坐标为（，）。‎ ‎（1）求此抛物线的解析式；‎ ‎（2）过点作线段的垂线交抛物线于点， 如果以点为圆心的圆与直线 相切，请判断抛物线的对称轴与⊙有怎样的位置关系，并给出证明；‎ ‎（3）已知点是抛物线上的一个动点，且位于，两点之间，过点作轴的平行线与交于点问：当点运动到什么位置时，线段的长度最大？并求出此时△的面积。‎ ‎27．（本题满分12分）‎ 如图1，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A的坐标为（－3，4），点C在x轴的正半轴上，直线AC交y轴于点M，AB边交y轴于点H．‎ ‎ （1）求直线AC的解析式；‎ ‎ （2）连接BM，如图2，动点P从点A出发，沿折线ABC方向以2个单位／秒的速度向终点C匀速运动，设△PMB的面积为S（S≠0），点P的运动时间为t秒，求S与t之间的函数关系式（要求写出自变量t的取值范围）；‎ ‎ （3）在（2）的条件下，当 t为何值时，∠MPB与∠BCO互为余角．‎ ‎（图2）‎ ‎28．（本题满分12分）‎ 甲船从A港出发顺流匀速驶向B港，行至某处，发现船上一救生圈不知何时落入水中，立刻原路返回，找到救生圈后，继续顺流驶向B港．乙船从B港出发逆流匀速驶向A港．已知救生圈漂流的速度和水流速度相同；甲、乙两船在静水中的速度相同．甲、乙两船到A港的距离y1、y2（km）与行驶时间x（h）之间的函数图象如图所示．‎ ‎（1）写出乙船在逆流中行驶的速度． ‎ ‎（2）求甲船在逆流中行驶的路程． ‎ ‎（3）求甲船到A港的距离y1与行驶时间x之间的函数关系式． ‎ ‎（4）求救生圈落入水中时，甲船到A港的距离． ‎ ‎【参考公式：船顺流航行的速度船在静水中航行的速度＋水流速度，船逆流航行的速度船在静水中航行的速度水流速度．】‎ 九年级数学中考模拟试卷答案 ‎ 一、选择题（每题3分，共30分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 选项 C D C C C B A C B D 二、填空题（每空2分，共16分）‎ ‎11．； 12．； 13．；14．； 15． ； 16．；17．； 18．‎ 三、解答题(共86分)‎ ‎19． 计算（本题8分）‎ ‎（1） 解： ……3分 ‎ ……4分 ‎20.（本题8分） ‎ ‎ （1）解方程：‎ 解： ……2分 ‎ ……3分 经检验x=2是原方程的增根，原方程无解。‎ ‎……4分 ‎（2）‎ 解：……3分 ‎ ……4分 ‎（2）解不等式组并 把解集在数轴上表示出来.‎ 解得……1分 ‎……2分 ‎……3分 数轴上表示出来（略）……4分 A D C B E ‎21.（本题6分）⑴求证：CD=BE．‎ ‎⑵若AD=3，DC=4，求AE． ‎ ‎⑴Rt△ADC≌Rt△CEB……3分 ‎∴CD=BE…4分 ‎ ⑵AE=2……6分 ‎22.（本题6分）‎ ‎ (树状图或列表正确)……………………3分 ‎∴P点可能的坐标有9种，（-3，-1），（-3,0），（-3，2），（0，-1），（0,0），（0，2），（-2，-1），（-2,0），（-2，2），---------------------------‎ ‎------------------------------4分 ‎（2）P点落在坐标轴上的可能有5种：（-3,0）（0，-1），（0,0），（0，2），（-2,0），∴概率为. 6分 ‎ ‎ ‎23．（本题6分）‎ 解：（1）300人……2分，图画对…………4分 （2）240人…………6分 C ‎60°‎ ‎38°‎ B D E ‎23°‎ A F ‎24.（本题7分）（1）求的度数；（2）求这棵大树折断前的高度？（结果精确到个位，参考数据：，，）‎ ‎(1) ……2分 ‎（2） ……6分 答：这棵大树折断前的高度约为‎10米。……7分 ‎25.（本题9分）‎ ‎6cm ‎6cm A B C D ‎8cm ‎6cm ‎4cm A B C D ‎8cm A B D ‎8cm C 解：由勾股定理得：AB=则 如图（1）AD=AB=‎10 cm时，BD=‎12cm，S==‎48 cm；……3分 ‎ ‎ 如图（2）BD=AB=‎10 cm时，S==‎40cm ……6分 如图（3）线段AB的垂直平分线交BC延长线于点D， S==；……9分 ‎（每种画图正确得2分，面积得1分）‎ ‎ 26.（本题10分）‎ 解：（1）……2分 ‎（2）抛物线的对称轴与⊙相交. ……3分 算出⊙半径为 ……5分 点C到对称轴的距离为 ‎∴抛物线的对称轴与⊙相交……6分 ‎（3）……7分 设则，……8分 当m=3时PQ的最大值为，此时,……9分 ……10分 ‎-----------------------密----------封----------线----------内----------请----------不----------要----------答----------题---------------------‎ ‎（图2）‎ ‎27．（本题12分）‎ 解：（1）……2分 ‎(2)， ……4分 ‎……7分 ‎(3), ……9分 ‎……12分 ‎28．（本题12分）‎ ‎ ‎ ‎27、解：（1）乙船在逆流中行驶的速度为‎6km/h． ………………………2分 ‎（2）甲船在逆流中行驶的路程为(km)． ………………………4分 ‎（3）设甲船顺流的速度为km/h，‎ 由图象得． ‎ 解得a9． ………………………6分 当0≤x≤2时，． ………………………7分 当2≤x≤2.5时，设．‎ 把，代入，得．‎ ‎∴．………………………8分 当2.5≤x≤3.5时，设．‎ 把，代入，得．‎ ‎∴． ………………………9分 ‎（4）水流速度为(km/h)．‎ 设甲船从A港航行x小时救生圈掉落水中．‎ 根据题意，得． ‎ 解得．．‎ 即救生圈落水时甲船到A港的距离为‎13.5 km． ………………………12分