- 139.50 KB
- 2021-05-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2017年中考数学总复习压轴题
动点专题
三角形
1、如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:
(1)当t=2时,判断△BPQ的形状,并说明理由;
(2)设△BPQ的面积为S(cm2),求S与t的函数关系式;
2、如图,已知中,厘米,厘米,点为的中点.
(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,与是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使与全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿三边运动,求经过多长时间点P与点Q第一次在的哪条边上相遇?
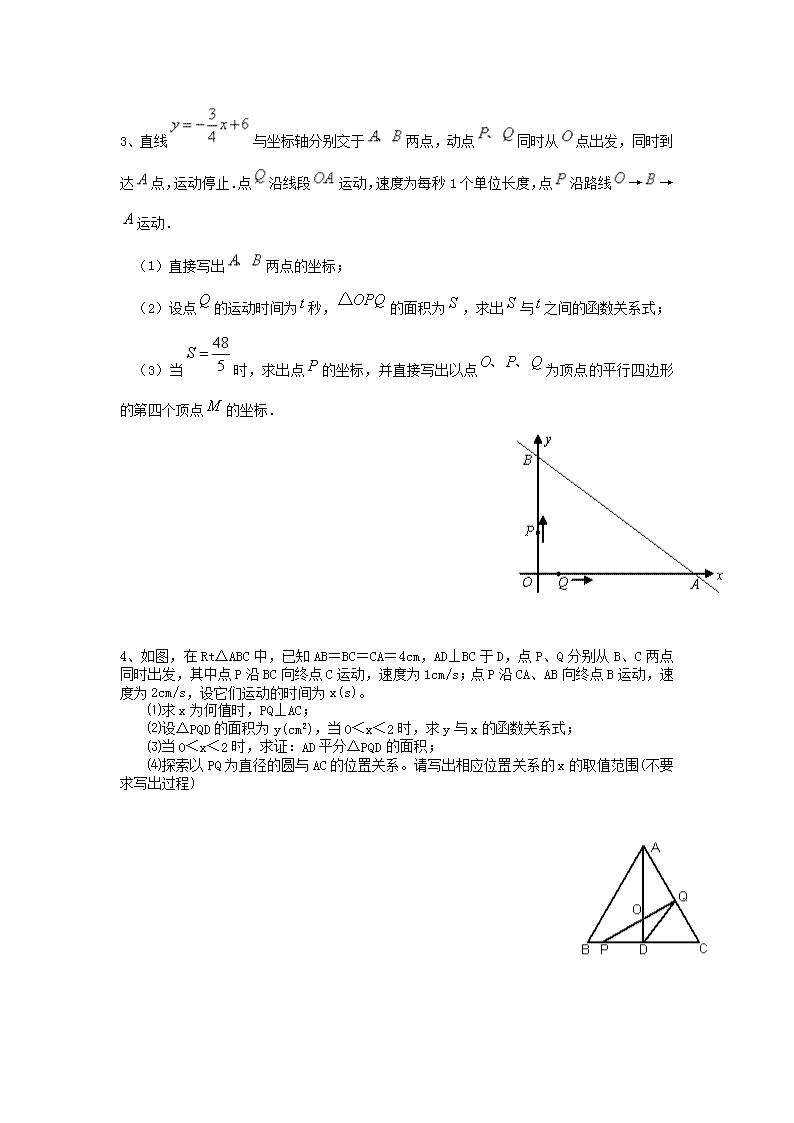
3、直线与坐标轴分别交于两点,动点同时从点出发,同时到达点,运动停止.点沿线段 运动,速度为每秒1个单位长度,点沿路线→→运动.
(1)直接写出两点的坐标;
(2)设点的运动时间为秒,的面积为,求出与之间的函数关系式;
(3)当时,求出点的坐标,并直接写出以点为顶点的平行四边形的第四个顶点的坐标.
4、如图,在Rt△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点P沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s)。
⑴求x为何值时,PQ⊥AC;
⑵设△PQD的面积为y(cm2),当0<x<2时,求y与x的函数关系式;
⑶当0<x<2时,求证:AD平分△PQD的面积;
⑷探索以PQ为直径的圆与AC的位置关系。请写出相应位置关系的x的取值范围(不要求写出过程)
5、在Rt△ABC中,∠C=90°,AC = 3,AB = 5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).
(1)当t = 2时,AP = ,点Q到AC的距离是 ;
(2)在点P从C向A运动的过程中,求△APQ的面积S与t的函数关系式;(不必写出t的取值范围)
(3)在点E从B向C运动的过程中,四边形QBED能否成为直角梯形?若能,求t的值.若不能,请说明理由;
(4)当DE经过点C 时,请直接写出t的值.
6、如图,在中,,,,分别是边的中点,点从点出发沿方向运动,过点作于,过点作交于,当点与点重合时,点停止运动.设,.(1)求点到的距离的长;
(2)求关于的函数关系式(不要求写出自变量的取值范围);
(3)是否存在点,使为等腰三角形?若存在,请求出所有
满足要求的的值;若不存在,请说明理由.
四边形
1、如图5,等腰梯形ABCD中,AD∥BC,AD=3cm,BC=7cm, ∠B=,P为下底BC上一点(不与B、C重合),连结AP,过P点作PE交DC于E,使得∠APE=∠B.
⑴求证: △ABP∽△PCE;
⑵求等腰梯形的腰AB的长;
⑶在底边BC上是否存在一点P,使得DE:EC=5:3,如果存在,求BP的长;如果不存在,请说明理由.
2、如图,在矩形ABCD中,AB=12厘米,BC=6厘米,点P沿AB边从点A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D开始向点A以1厘米/秒的速度移动。如果P、Q同时出发,用秒表示移动的时间(0≤≤6)。
(1)当为何值时,△QAP为等腰直角三角形?
(2)求四边形QAPC的面积,并提出一个与计算结果有关的结论;
(3)当为何值时,以点Q、A、P为顶点的三角形与△ABC相似?
5.[思维点拔]
① 由图形可知,当△APQ为等腰直角三角形时,QA=AP,由此可列出关于方程,从而求出的值;
② 将四边形QAPC分割成△QAC和△APC,先求出三角形的面积,从而得到四边形QAPC的面积;
③ 以点Q、A、P为顶点的三角形与△ABC相似,这个问题因不管P、Q如何运动,△QAP的∠QAP都为直角,与△ABC的∠ABC相等,所以考虑“对应边”应分QA与BC为对应边或AQ与AB为对应边的两种情况讨论。
3、如图1,在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12.动点P从D点出发沿DC以每秒1个单位的速度向终点C运动,动点Q从C点出发沿CB以每秒2个单位的速度向B点运动.两点同时出发,当P点到达C点时,Q点随之停止运动.
(1)梯形ABCD的面积等于 ;
(2)当PQ∥AB时,P点离开D点的时间等于 秒;
(3)当P,Q,C三点构成直角三角形时,P点离开D点多少时间?
4、如图,在梯形中,动点从点出发沿线段以每秒2个单位长度的速度向终点运动;动点同时从点出发沿线段以每秒1个单位长度的速度向终点运动.设运动的时间为秒.
(1)求的长.
(2)当时,求的值.
(3)试探究:为何值时,为等腰三角形.
5、如图①,正方形 ABCD中,点A、B的坐标分别为(0,10),(8,4),
点C在第一象限.动点P在正方形 ABCD的边上,从点A出发沿A→B→C→D匀速运动,
同时动点Q以相同速度在x轴正半轴上运动,当P点到达D点时,两点同时停止运动,
设运动的时间为t秒.
(1)当P点在边AB上运动时,点Q的横坐标(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;
(2)求正方形边长及顶点C的坐标;
(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标;
(4)如果点P、Q保持原速度不变,当点P沿A→B→C→D匀速运动时,OP与PQ能否相等,若能,写出所有符合条件的t的值;若不能,请说明理由.
6、如图所示,在平面直角坐标中,四边形OABC是等腰梯形,BC∥OA,OA=7,AB=4,∠ COA=60°,点P为x轴上的—个动点,点P不与点0、点A重合.连结CP,过点P作PD交AB于点D.
(1)求点B的坐标;
(2)当点P运动什么位置时,△OCP为等腰三角形,求这时点P的坐标;
(3)当点P运动什么位置时,使得∠CPD=∠OAB,且=,求这时点P的坐标。