2014中考数学模拟试卷 17页

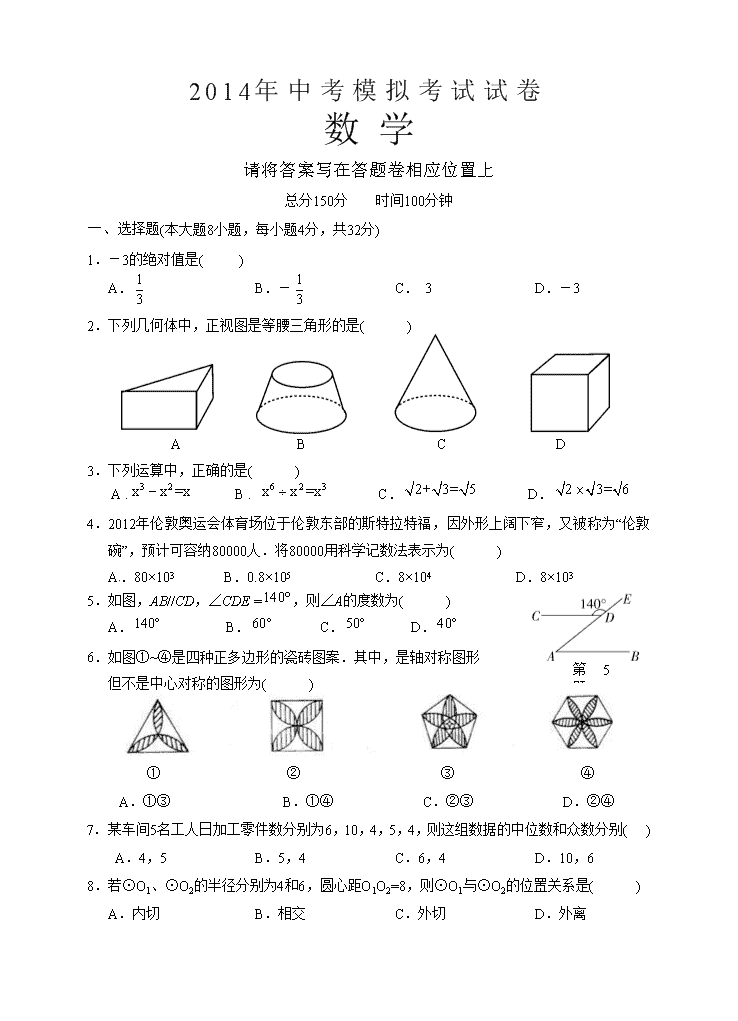
‎2014年中考模拟考试试卷 数 学 请将答案写在答题卷相应位置上 总分150分 时间100分钟 一、选择题(本大题8小题，每小题4分，共32分)‎ ‎1．－3的绝对值是( )‎ A． B．－ C． 3 D．－3‎ ‎2．下列几何体中，正视图是等腰三角形的是( )‎ ‎ ‎ ‎ A B C D ‎3．下列运算中，正确的是( )‎ A . B . C． D．‎ ‎4．2012年伦敦奥运会体育场位于伦敦东部的斯特拉特福，因外形上阔下窄，又被称为“伦敦碗”，预计可容纳80000人．将80000用科学记数法表示为( )‎ 第5题 A．80×103 B．0.8×105 C．8×104 D．8×103‎ ‎5．如图，AB//CD，∠CDE =，则∠A的度数为( )‎ ‎ A． B． 　　 C．　 　D．‎ ‎6．如图①~④是四种正多边形的瓷砖图案．其中，是轴对称图形 ‎ 但不是中心对称的图形为(　 　)‎ ‎ 　　①　　　　　　　　　②　　　　　　　　　　③　　　　　　　　　④‎ ‎ A．①③ B．①④ C．②③ D．②④‎ ‎7．某车间5名工人日加工零件数分别为6，10，4，5，4，则这组数据的中位数和众数分别( 　)‎ ‎　　A．4，5 B．5，4 C．6，4 D．10，6‎ ‎8．若⊙O1、⊙O2的半径分别为4和6，圆心距O1O2=8，则⊙O1与⊙O2的位置关系是( )‎ A．内切 B．相交 C．外切 D．外离 二、填空题(本大题5小题，每小题4分，共20分)‎ ‎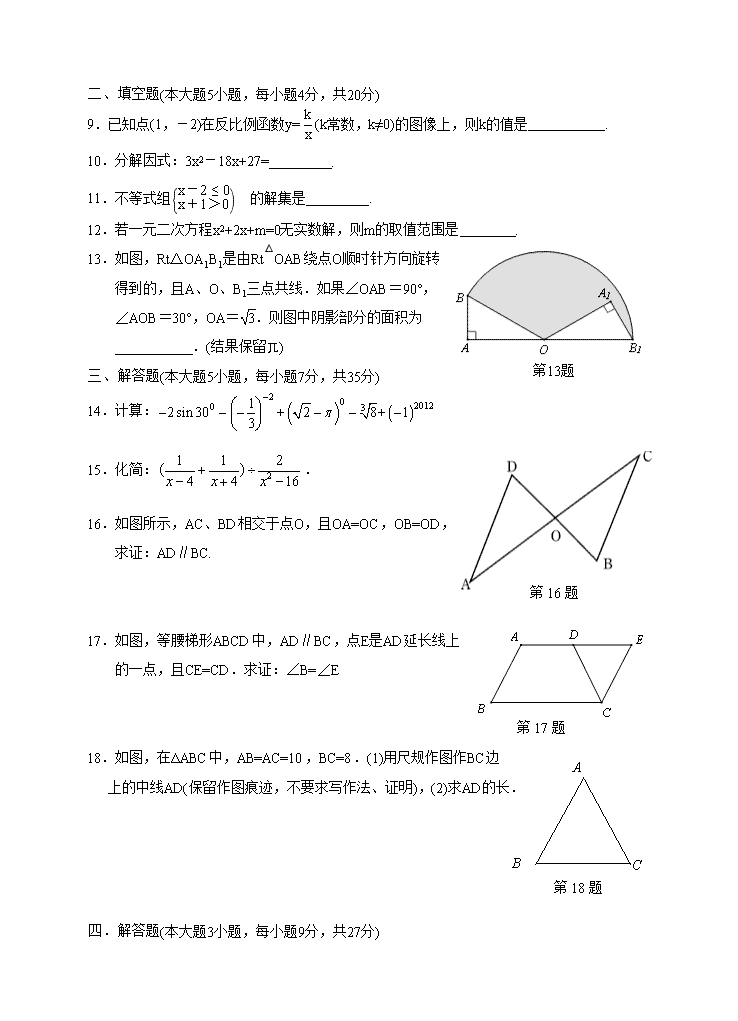9．已知点(1，－2)在反比例函数y=(k常数，k≠0)的图像上，则k的值是 .‎ ‎10．分解因式：3x2－18x+27=_________.‎ ‎11．不等式组　的解集是_________.‎ ‎12．若一元二次方程x2+2x+m=0无实数解，则m的取值范围是 .‎ 第13题 ‎13．如图，Rt△OA1B1是由Rt△OAB绕点O顺时针方向旋转 得到的，且A、O、B1三点共线．如果∠OAB＝90°，‎ ‎∠AOB＝30°，OA＝．则图中阴影部分的面积为 ‎ ．(结果保留π)‎ 三、解答题(本大题5小题，每小题7分，共35分)‎ ‎14．计算：‎ 第16题 ‎15．化简：．‎ ‎16．如图所示，AC、BD相交于点O，且OA=OC，OB=OD，‎ ‎ 求证：AD∥BC.‎ 第17题 ‎ ‎ ‎17．如图，等腰梯形ABCD中，AD∥BC，点E是AD延长线上 ‎ 的一点，且CE=CD．求证：∠B=∠E 第18题 A B ‎18．如图，在ΔABC中，AB=AC=10，BC=8．(1)用尺规作图作BC边 ‎ 上的中线AD(保留作图痕迹，不要求写作法、证明)，(2)求AD的长．‎ C 四．解答题(本大题3小题，每小题9分，共27分)‎ ‎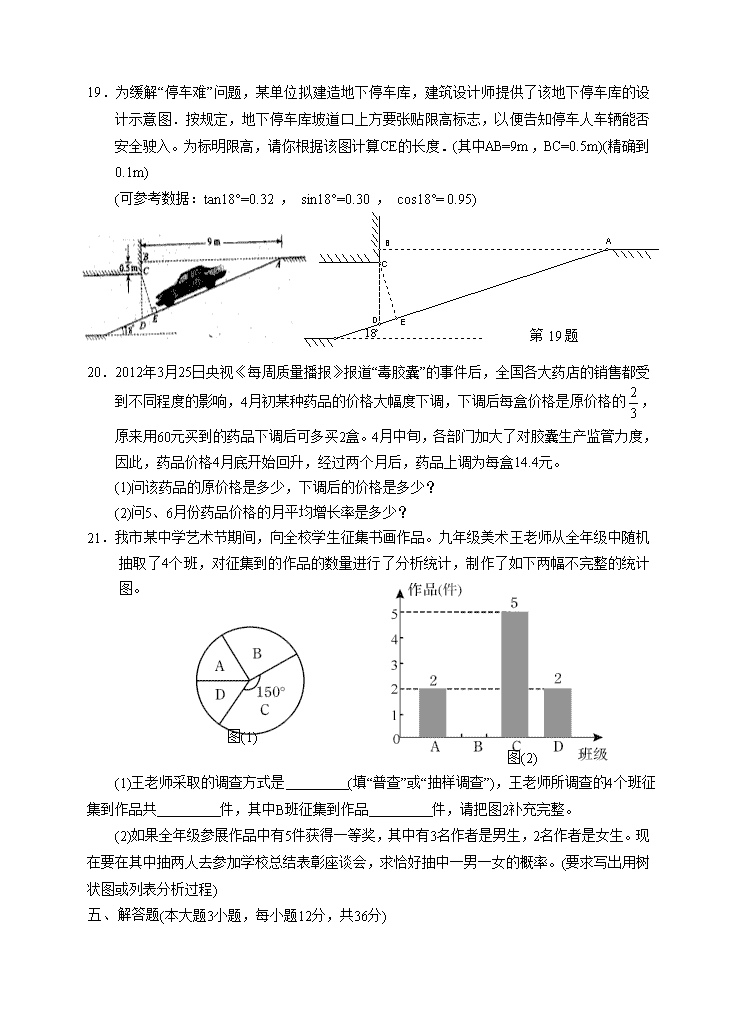19．为缓解“停车难”问题，某单位拟建造地下停车库，建筑设计师提供了该地下停车库的设计示意图．按规定，地下停车库坡道口上方要张贴限高标志，以便告知停车人车辆能否安全驶入。为标明限高，请你根据该图计算CE的长度．(其中AB=9m，BC=0.5m)(精确到0.1m)‎ ‎　　(可参考数据：tan18°=0.32 ， sin18°=0.30 ， cos18°= 0.95)‎ 第19题 ‎20．2012年3月25日央视《每周质量播报》报道“毒胶囊”的事件后，全国各大药店的销售都受 ‎　　到不同程度的影响，4月初某种药品的价格大幅度下调，下调后每盒价格是原价格的，‎ ‎　　原来用60元买到的药品下调后可多买2盒。4月中旬，各部门加大了对胶囊生产监管力度，因此，药品价格4月底开始回升，经过两个月后，药品上调为每盒14.4元。‎ ‎　　(1)问该药品的原价格是多少，下调后的价格是多少？‎ ‎　　(2)问5、6月份药品价格的月平均增长率是多少？‎ ‎21．我市某中学艺术节期间，向全校学生征集书画作品。九年级美术王老师从全年级中随机抽取了4个班，对征集到的作品的数量进行了分析统计，制作了如下两幅不完整的统计图。‎ ‎ 　　图(1)‎ ‎　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　图(2)‎ ‎　　(1)王老师采取的调查方式是 (填“普查”或“抽样调查”)，王老师所调查的4个班征集到作品共 件，其中B班征集到作品 件，请把图2补充完整。‎ ‎　　‎ ‎(2)如果全年级参展作品中有5件获得一等奖，其中有3名作者是男生，2名作者是女生。现在要在其中抽两人去参加学校总结表彰座谈会，求恰好抽中一男一女的概率。(要求写出用树状图或列表分析过程)‎ 五、解答题(本大题3小题，每小题12分，共36分)‎ ‎22. 先观察下列等式，然后用你发现的规律解答下列问题．‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎……‎ ‎　　(1) 计算 ．‎ ‎　　(2)探究 ．(用含有的式子表示)‎ ‎　　(3)若 的值为，求的值．‎ ‎23．如图，在Rt△ABC中，∠ABC=90°，D是AC的中点，⊙O经过A、B、‎ ‎　　D三点，CB的延长线交⊙O于点E.‎ ‎　　(1)求证AE=CE； (4分)‎ ‎　　(2)EF与⊙O相切于点E，交AC的延长线于点F，‎ ‎①若CD=CF=2cm，求⊙O的直径；(4分)‎ ‎②若 (n>0)，求sin∠CAB. (4分)‎ 第23题 ‎24．如图，在平面直角坐标系中，抛物线y＝ax2＋bx＋6经过点A(－3，0)和点B(2，0)．直线y＝h(h为常数，且0＜h＜6)与BC交于点D，与y轴交于点E，与AC交于点F，与抛物线在第二象限交于点G．‎ ‎　　(1)求抛物线的解析式；(3分)‎ ‎　　(2)连接BE，求h为何值时，△BDE的面积最大；(4分)‎ ‎　　(3)已知一定点M(－2，0)．问：是否存在这样的直线y＝h，使△OMF是等腰三角形，若存在，请求出h的值和点G的坐标；若不存在，请说明理由．(5分)‎ ‎　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　第24题 ‎2013年中考模拟考试试卷 数学答题卷 题号 一 二 三 四 五 总 分 ‎19‎ ‎20‎ ‎21‎ ‎22‎ ‎23‎ ‎24‎ 得分 说明：数学科考试时间为100分钟，满分为150分 注意事项：‎ ‎1．答题前，考生务必用黑色字迹的钢笔或签字笔在答题卷上指定的栏目填写。‎ ‎2．保持卡面清洁，不要折叠，不要弄破。‎ ‎3．请注意题号顺序。‎ ‎ 一、选择题答题区 ‎1．用2B铅笔填涂；‎ ‎2．修改时用塑料橡皮擦干净后，重新填涂所选项；‎ ‎3．填涂的正确方法是：■ ‎ ‎1‎ ‎[A]‎ ‎[B]‎ ‎[C]‎ ‎[D]‎ ‎5‎ ‎[A]‎ ‎[B]‎ ‎[C]‎ ‎[D]‎ ‎2‎ ‎[A]‎ ‎[B]‎ ‎[C]‎ ‎[D]‎ ‎6‎ ‎[A]‎ ‎[B]‎ ‎[C]‎ ‎[D]‎ ‎3‎ ‎[A]‎ ‎[B]‎ ‎[C]‎ ‎[D]‎ ‎7‎ ‎[A]‎ ‎[B]‎ ‎[C]‎ ‎[D]‎ ‎4‎ ‎[A]‎ ‎[B]‎ ‎[C]‎ ‎[D]‎ ‎8‎ ‎[A]‎ ‎[B]‎ ‎[C]‎ ‎[D]‎ ‎ 二、填空题(每小题4分，共20分)(用0.5毫米黑色墨水签字笔作答)‎ ‎9．__________________； 10．________________； 11．________________；‎ ‎12．_________________； 13．________________。‎ ‎ 三、解答题(每小题7分，共35分)(用0.5毫米黑色墨水签字笔作答)‎ ‎　 14．解 ‎ 15．解：‎ ‎ 16．解：‎ 第16题 第17题 ‎ 17．证明：‎ ‎ ‎ 第18题 A B C ‎ 18．解：(1) ‎ ‎ ‎ ‎ (2)‎ ‎ 四．解答题(每小题9分，共27分)(用0.5毫米黑色墨水签字笔作答)‎ ‎ 19．解： ‎ ‎ ‎ ‎ 20．解：(1)‎ ‎ (2)‎ ‎ 21．(1)______________; __________________; ______________‎ ‎ ‎ ‎　　　　　　　　　　　　　　　　　　　　　　　　　　　　图(2)‎ ‎ (2)‎ ‎ 五、解答题(每小题12分，共36分)(用0.5毫米黑色墨水签字笔作答)‎ ‎　22．解：(1)___________________ (2) __________________ ‎ ‎　(3)‎ ‎ 23．(1)证明：‎ ‎ ‎ ‎ (2)解：①‎ ‎　②‎ ‎ 24．解：(1)‎ ‎ ‎ ‎　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　第24题 ‎　(2)‎ ‎　(3)‎ ‎2013年中考模拟考试试卷 数学参考答案 一、选择题(本大题8小题，每小题4分，共32分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 C ‎ C D C D A ‎ B B 二、填空题(本大题共5小题，每小题4分，共20分)‎ ‎　9．-2 10．3(x-3)2 11．-1＜x≤2 　12． m＞1 13． ‎ 三、解答题(本大题共5小题，每小题7分，共35分)‎ ‎14．解：　原式=。…………………5分 ‎ 　　 =-10…………………………7分 ‎15．解：原式= ………………… 4分 ‎ 　　　　= ………………… 6分 ‎ =………………… 7分 第16题 ‎16．证明：在△AOD和△COB中，‎ ‎∵OA=OC，OB=OD，且∠AOD=∠COB，…………3分 ‎∴△AOD≌△COB(SAS)。………………4分 ‎∴∠A=∠C。………………………………5分 ‎∴AD∥BC。……………………………7分 ‎17．证明：∵四边形ABCD是等腰梯形，‎ 第17题 ‎∴∠B=∠1。……………2分 ‎ ∵AD∥BC，‎ ‎∴∠1=∠2。……………4分 ‎ ∵CE=CD，‎ ‎∴∠2=∠E。……………6分 ‎∴∠B=∠E。……………7分 ‎18．解：(1)作图正确得2分(不保留痕迹的得1分)…………2分 ‎ (2)在△ABC中，AB=AC，AD是△ABC的中线，‎ ‎ ∴AD⊥BC，…………………………………………………4分 ‎ .…………………………5分 ‎ 　 在Rt△ABD中，AB＝10，BD＝4，，……6分 第19题 ‎ 　　.…………………7分 四、解答题(本大题共3小题，每小题9分，共27分)‎ ‎19．解：由题意得：∠A=18°，……………1分 ‎　　　在Rt△ABD中，∵AB=9，‎ ‎　　　∴BD=AB•tan18°≈2.88，……………4分 ‎　　　∴CD=BD-BC=2.38，………………5分 ‎　　　∵∠A+∠CDA=90°，∠DCE+∠CDE=90°，……6分 ‎　　　∴∠DCE=∠A=18°，………………7分 ‎　　　∴在Rt△ABD中，CE= CD•cos18°≈2.3．…………9分 ‎20．解：(1)设该药品的原价格是x元/盒，则下调后每盒价格是x元/盒。‎ ‎ 根据题意，得，解得x=15。…………………………3分 ‎ 经检验，x=15是原方程的解。‎ ‎ ∴x=15，x=10。…………………………4分 ‎ 答：该药品的原价格是15元/盒，则下调后每盒价格是10元/盒。……………5分 ‎　　(2)设5、6月份药品价格的月平均增长率是a，‎ ‎　　　　　根据题意，得，…………………………7分 ‎　　解得(不使题意，舍去)。…………………………8分 ‎ 答：5、6月份药品价格的月平均增长率是20%。…9分 ‎21．解：抽样调查；‎ ‎ 12；3。‎ ‎ 把图2补充完整如下：……4分 ‎ (每空1分)‎ ‎(2)用树状图(列表)分析如下：‎ 共有20种机会均等的结果，其中一男一女占12种，‎ ‎　　　∴P(一男一女)=，即恰好抽中一男一女的概率是。……………9分 五、解答题(本大题共3小题，每小题12分，共36分)‎ ‎22．解：(1) …………3分 (2) …………6分 ‎ (3)‎ ‎　　 　=+ ┄ +‎ ‎　　　== 9分 ‎　　　由= 解得 11分 ‎　　　经检验是方程的根，∴ 12分 ‎23．证明：(1)连接DE，∵∠ABC=90° ∴∠ABE=90°，‎ ‎　　∴AE是⊙O直径．………………… 1分 ‎　　∴∠ADE=90°，∴DE⊥AC．………………… 2分 ‎　　又∵D是AC的中点，∴DE是AC的垂直平分线．………3分 ‎　　∴AE=CE．…………………4分 ‎ ‎(2)∵AE是⊙O直径，EF是⊙O的切线，∴∠ADE=∠AEF=90°，‎ ‎①在△ADE和△AEF中，‎ ‎ ∵∠ADE=∠AEF=90°，∠DAE=∠FAE，‎ ‎ ∴△ADE∽△AEF．…………………6分 ‎ ∴，‎ ‎ ∴…………7分 ‎ ∴AE=2cm．…………8分 ‎ ②由(1)知AE=CE，∴∠1=∠DAE ∵∠ABC=90° ∴∠CAB+∠1=90°‎ ‎ ∴∠ADE=90° ∴∠DAE+∠2 =90° ∴∠CAB=∠2‎ ‎ 又∵△ADE∽△AEF． ∴．即AE2=AD·AF 9分 ‎ ∵，AD=CD，∴CF=nAD，∴AF=(2+n)AD， ‎ ‎ ∴ AE2=AD·AF=(2+n)AD2…………10分 ‎ ∴==． 11分 ‎ ∵∴sin∠CAB=sin∠2 ==． 12分 ‎24．解：(1)∵抛物线y＝ax2＋bx＋6经过点A(－3，0)和点B(2，0)，‎ ‎ ∴。解得。‎ ‎∴抛物线的解析式为y＝。…………3分 ‎ (2)把x＝0代入y＝，得y＝6。‎ ‎ ∴点C的坐标为(0，6)．‎ ‎ 　设经过点B和点C的直线的解析式为y＝mx＋n，则，解得 。‎ ‎ ∴经过点B和点C的直线的解析式为y＝－3x＋6。‎ ‎ ∵点E在直线y＝h上，∴点E的坐标为(0，h)。‎ ‎ ∴OE＝h。‎ ‎ ∵点D在直线y＝h上，∴点D的纵坐标为h。‎ ‎ 把y＝h代入y＝－3x＋6，得h＝－3x＋6．解得x＝。∴点D的坐标为(，h)。‎ ‎ ∴DE＝．‎ ‎　　另：∵FD//AB　∴=得=　　　　∴　DE＝．‎ ‎ ∴S△BDE＝•OE•DE＝•h•＝－(h－3)2＋．‎ ‎ ∵－＜0且0＜h＜6，‎ ‎ ∴当h＝3时，△BDE的面积最大，最大面积是．…………………………7分 ‎ (3)存在符合题意的直线y＝h．‎ ‎ 设经过点A和点C的直线的解析式为y＝kx＋p，则，解得 ．‎ ‎ ∴经过点A和点C的直线的解析式为y＝2x＋6．‎ ‎ 把y＝h代入y＝2x＋6，得h＝2x＋6．解得x＝．‎ ‎ ∴点F的坐标为(，h)。‎ ‎ 在△OFM中，OM＝2，OF＝，MF＝．‎ ‎ ①若OF＝OM，则＝2，整理，得5h2－12h＋20＝0．‎ ‎ ∵△＝(－12)2－4×5×20＝－256＜0，∴此方程无解．∴OF＝OM不成立．‎ ‎ ②若OF＝MF，则＝，解得h＝4．‎ ‎ 把y＝h＝4代入y＝，得＝4，解得x1＝－2，x2＝1．‎ ‎ ∵点G在第二象限，∴点G的坐标为(－2，4)．‎ ‎ ③若MF＝OM，则=2，解得h1＝2，h2＝－(不合题意，舍去)．‎ ‎ 把y＝h1＝2代入y＝，得＝2．解得x1＝，x2＝．‎ ‎ ∵点G在第二象限，∴点G的坐标为(，2)．‎ ‎ 综上所述，存在这样的直线y＝2或y＝4，使△OMF是等腰三角形，当h＝4时，点G的坐标为(－2，4)；当h＝2时，点G的坐标为(，2)。………………12分