2014四川省巴中市中考数学试卷 15页

2014 年四川省巴中市中考数学试卷 （满分 150 分，考试时间 120 分钟） 一、选择题（本大题共 10 小题，每小题 3 分，满分 30 分，在每小题给出的四个选项中， 只有一项是符合题目要求的。） 1.（2014 四川省巴中市，1，3 分） 的相反数是（ ） A. B. C. -5 D. 5 【答案】B 2. （2014 四川省巴中市，2，3 分） 2014 年三月发生了一件举国悲痛的空难事件——马航失联，该飞机上有中国公民 154 名， 噩耗传来后，我国为了搜寻生还者及找到失联飞机，在搜救方面花了大量的人力物力，已 花费人民币大约 934 千万元，把 934 千万元用科学记数法表示为（ ）元 A. B. C. D. 【答案】D 3.（2014 四川省巴中市，3，3 分） 如图 1，CF 是 的外角 的平分线，且 CF//AB， =50°，则∠B 的度 数为（ ） A. 80° B. 40° C. 60° D. 50° 【答案】D 4. （2014 四川省巴中市，4，3 分） 要使式子 有意义，则 m 的取值范围是（ ） A. m>-1 B. m≥-1 C.m>-1 且 m≠1 D. m≥-1 且 m≠1 【答案】D 5. （2014 四川省巴中市，5，3 分） 如图 2，两个大小不同的实心球在水平面靠在一起组成如图所示的几何体，则该几何体的 左视图是（ ） A.两个外切的圆 B.两个内切的圆 C.两个内含的圆 D. 一个圆 A B MC F 1- 5 1- 5 1 5 29.34 10× 30.934 10× 99.34 10× 109.34 10× ABC ACM∠ ACF∠ 1 1 m m + − 【答案】B 6. （2014 四川省巴中市，6，3 分） 今年我市有 4 万名考生参加中考，为了了解这些考生的数学成绩，从中抽取 2000 名考生的 数学成绩进行统计分析，在这个问题中，下列说法：①这的 4 万名考生的数学中考成绩的 全体是总体；②每个考生是个体；③2000 名考生是总体的一个样本；④样本容量是 2000， 其中说法正确的有( ) A. 4 个 B. 3 个 C. 2 个 D. 1 个 【答案】C 7. （2014 四川省巴中市，7，3 分） 下列汽车标志中既是轴对称图形又是中心对称图形的是（ ） A. B. C. D. 【答案】C 8. jm（2014 四川省巴中市，8，3 分） 在 Rt△ABC 中，∠C=90°, ，则 tanB 的值为（ ） A. B. C. D. 【答案】D 9. js（2014 四川省巴中市，9，3 分） 已知直线 ，其中 m、n 是常数，且满足：m+n=6，mn=8，那么该直线经过（ ） A.第二、三、四象限 B. 第一、二、三象限 C. 第一、三、四象限 D. 第一、二、四象限 【答案】B 10. 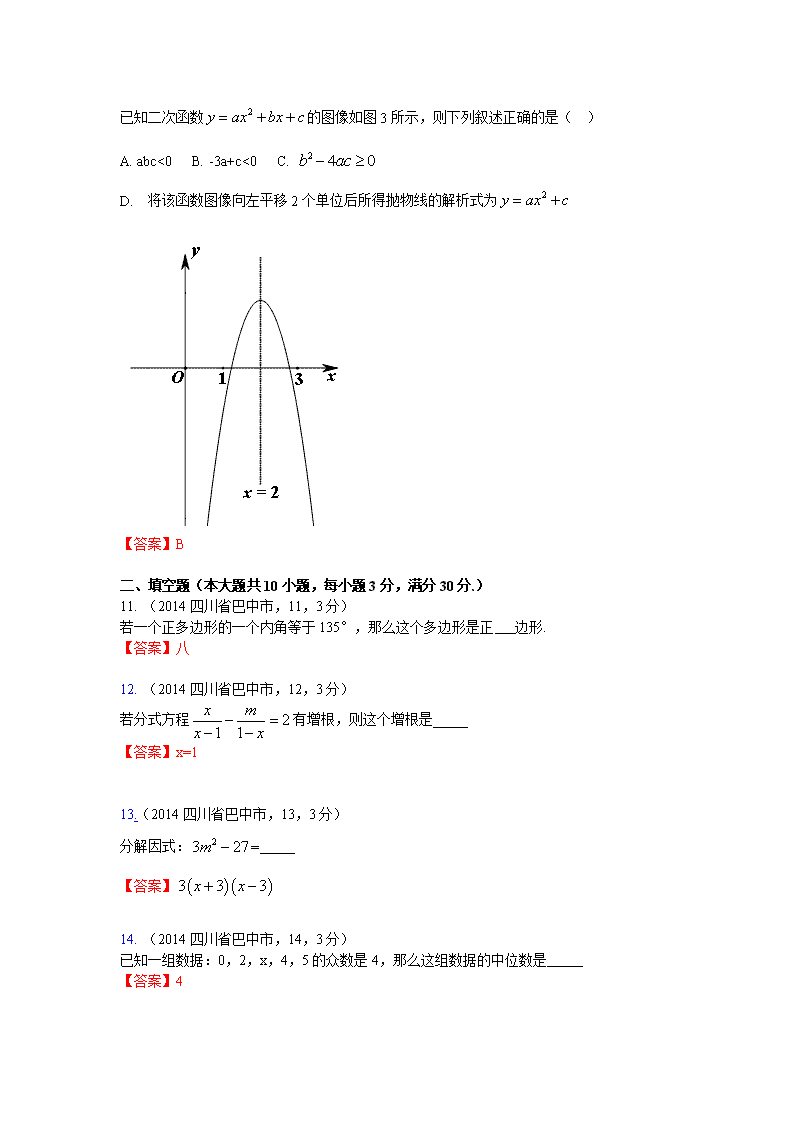j（2014 四川省巴中市，10，3 分） 图2 5sin 13A = 12 13 5 12 13 12 12 5 y mx n= + 已知二次函数 的图像如图 3 所示，则下列叙述正确的是（ ） A. abc<0 B. -3a+c<0 C. D. 将该函数图像向左平移 2 个单位后所得抛物线的解析式为 【答案】B 二、填空题（本大题共 10 小题，每小题 3 分，满分 30 分.） 11. （2014 四川省巴中市，11，3 分） 若一个正多边形的一个内角等于 135°，那么这个多边形是正 边形. 【答案】八 12. （2014 四川省巴中市，12，3 分） 若分式方程 有增根，则这个增根是 【答案】x=1 13.（2014 四川省巴中市，13，3 分） 分解因式： = 【答案】 14. （2014 四川省巴中市，14，3 分） 已知一组数据：0，2，x，4，5 的众数是 4，那么这组数据的中位数是 【答案】4 x y x = 2 O 31 2y ax bx c= + + 2 4 0b ac− ≥ 2y ax c= + 21 1 x m x x − =− − 23 27m − ( )( )3 3 3x x+ − 15. （2014 四川省巴中市，15，3 分） 若圆锥的轴截面是一个边长为 4 的等边三角形，则这个圆锥的侧面展开后所得的扇形的圆 心角的度数是 【答案】180° 16.（2014 四川省巴中市，16，3 分） 菱形的两条对角线分别是方程 的两实根，则菱形的面积为 【答案】24 17. jsc（2014 四川省巴中市，17，3 分） 如图 4，已知 A、B、C 三点在⊙O 上，AC⊥BD 于 D，∠B=55°，则∠BOC 的度数是 【答案】70° 18.jscm（2014 四川省巴中市，18，3 分） 如图 5，已知直线 与 x 轴、y 轴分别交于 A、B 两点，把△AOB 绕点 A 按顺 时针方向旋转 90°后得到△AO1B1 ，则点 B1 的坐标是 【答案】（7，3） 图4 D C OA B y x 图5 B1O1 A B O 2 14 48 0x x− + = 4 43y x= − + 19. （2014 四川省巴中市，19，3 分）在四边形 ABCD 中，①AB∥CD，②AD∥BC，③ AB=CD，④AD=BC，在这四个条件中任选两个作为已知条件，能判定四边形 ABCD 是平行 四边形的概率是 【答案】 20. （2014 四川省巴中市，20，3 分） 图 6 是我国古代数学家杨辉最早发现的，称为“杨辉三角形”.它的出现比西方要早五百年 左右，由此可见我国古代数学的成就是非常值得中华民族自豪的！“杨辉三角形”中有许 多规律，如它的每一行数字正好对应了 （n 为自然数）的展开式中 a 按次数从大到 小排列的项的系数，例如 展开式中的系数 1、2、1 恰好对应图中 第三行的数字；再如 展开式中的系数 1、3、3、1 恰好对 应图中第四行的数字.请认真观察此图，写出 的展开式为 【答案】 三、解答题（本大题共 3 小题，每小题各 5 分，共 15 分） 21. （2014 四川省巴中市，21，5 分） 计算： 【答案】解：原式= = =5 22. （2014 四川省巴中市，22，5 分） 定义新运算：对于任意实数 a、b 都有 a△b=ab-a-b+1，等式右边是通常的加法、减法及乘 法运算，例如：2△3=2×4-2-4+1=8-6+1=3，请根据上述知识解决问题：若 3△x 的值大于 5 而小于 9，求 x 的取值范围. 【答案】解：∵ 且 3△x 的值大于 5 而小于 9 ∴ ，即 23. （2014 四川省巴中市，23，5 分） 先化简，再求值： ，其中 x 满足 【答案】解：原式= = 2 3 ( )na b+ ( )2 2 22a b a ab b+ = + + ( )3 3 2 2 33 3a b a a b ab b+ = + + + ( )4a b− 4 3 2 2 3 44 6 4a a b a b ab b− + − + ( )113 2 sin 45 tan 60 12 33 π − − + + − − − + −     ( )23 2 3 3 2 3 12 + × + − − − + 3 1 3 3 2 3 1+ + + − + 3 3 3 1 2 2x x x x= − − + = − 5 2 2 9x< − < 7 11 2 2x< < 2 22 4 4 421 1 x x x xxx x  − + + ++ − ÷ − −  2 4 3 0x x− + = ( )22 2 22 4 3 2 1 1 1 xx x x x x x x + − + − + −+ ÷ − − −  ( )2 2 1 1 2 x x x x + − − + = ∵ ∴ ∴ ， 又∵ ∴ ∴当 时，原式= = 四、操作与统计（24 题 8 分，25 题 7 分，共 15 分） 24. （2014 四川省巴中市，24，8 分） 如图 7，在平面直角坐标系 xoy 中，△ABC 三个顶点坐标分别为 A（-2，4），B（-2,1），C （-5,2） ①请画出△ABC 关于 x 轴对称的△A1B1C1；（3 分） ②将△A1B1C1 的三个顶点的横坐标与纵坐标同时乘以-2，得到对应的点 A2、B2、C2 ，请 画出△A2B2C2 ；（3 分） ③求△A1B1C1 与△A2B2C2 的面积比，即 S△A1B1C1:S△A2B2C2=________（不写解答过程，直 接写出结果）. (2 分) 【答案】解：①、②如图所示； y x C B A O 1 2x − + 2 4 3 0x x− + = ( )( )1 3 0x x− − = 1 1x = 2 3x = 1 0x − ≠ 1x ≠ 3x = 1 2x − + 1 5 − ③ 1：4 25. （2014 四川省巴中市，25，7 分） 巴中市对初三年级学生的体育、物理实验操作、化学实验操作成绩进行抽样调查，成绩评 定为 A、B、C、D 四个等级，现抽取这三种成绩共 1000 份进行统计分析，其中 A、B、 C、D 分别表示优秀、良好、合格、不合格四个等级，相关数据统计如表 1、图 8 所示. ①请将表 1 补充完整（直接填数据，不写解答过程）.（3 分） ②巴中市共有 40000 名学生参加测试，试估计该市初三年级学生化学实验操作合格及合格 以上大约有多少人？（2 分） ③在这 40000 名学生中，体育成绩不合格的大约有多少人？（2 分） A B C D 物理实验操作 120 90 20 化学实验操作 90 110 30 体 育 140 160 27 【答案】解：(1)如下表： A B C D 物理实验操作 120 70 90 20 y x C2 B2 A2 C1 B1 A1 C B A O 化学实验操作 物理实验操作 体育 图8 25% 30% 化学实验操作 90 110 30 20 体 育 123 140 160 27 （2） 答：巴中市 40000 名参加测试的学生，化学实验操作合格及合格以上大约有 36800 人； （3） 答：在这 40000 名学生中，体育成绩不合格的大约有 2400 人. 五、方程及解直角三角形的应用（26 题 8 分，27 题 10 分，共 18 分） 26. （2014 四川省巴中市，26，8 分） 某商店准备进一批季节性小家电，单价 40 元，经市场预测，销售定价为 52 元时，可售出 180 个. 定价每增加 1 元，销售量净减少 10 个；定价每减少 1 元，销售量净增加 10 个。因受 库存的影响，每批次进货个数不得超过 180 个。商店若将准备获利 2000 元，则应进货多少 个？定价多少元？ 【答案】解：（1）设定价为 x 元，则进货为 180-10（x-52）=180-10x+520=（700-10x）个， 所以（x-40）（700-10x）=2000， 解得 x1=50，x2=60； ∵每批次进货个数不得超过 180 个 ∴700-10x≤180 ∴x≥52 ∴x=60 当 x=60 时，700-10x=700-10×60=100 个； 答：商店若准备获利 2000 元，应进货 100 个，定价为 60 元. 27. （2014 四川省巴中市，27，10 分） 如图 9，一水库大坝的横断面为梯形 ABCD，坝顶 BC 宽 6 米，坝高 20 米，斜坡 AB 的坡 度 i=1:2.5，斜坡 CD 的坡角为 30°，求坝底 AD 的长度（精确到 0.1 米，参考数据： ， ，提示：坡度等于坡面的铅垂高度与水平长度之比。） 【答案】解：如图，分别过点 B、C 作 BE⊥AD、CF⊥AD 垂足分别为 E、F， 30° i=1:2.5 图9 DA CB 30° i=1:2.5 DA CB E F 90+110+30 40000=36800250 × 27 40000=2400450 × 2 1.414≈ 3 1.732≈ 由题意可知：BE=CF=20，BC=EF=6，∠D=30°， 在 Rt△ABE 中，i= ，即 ，∴AE=50 在 Rt△CDF 中，tan30°= ，即 ，∴DF= ∴AD=AE+EF+FD=50+6+11.5=67.5 六、推理（28 题 10 分，29 题 10 分，共 20 分） 28.（2014 四川省巴中市，28，10 分） 如图 10，在四边形 ABCD 中，点 H 是边 BC 的中点，作射线 AH，在线段 AH 及其延长线 上分别取点 E,F，连接 BE,CF. (1)请你添加一个条件，使得△BEH≌△CFH，你添加的条件是 ，（2 分）并证明。 （4 分） （2）在问题（1）中，当 BH 与 EH 满足什么关系时，四边形 BFCE 是矩形，请说明理由。 （4 分） 【答案】解：(1)添加条件：BE∥CF （答案不唯一） 证明：如图，∵BE∥CF ∴∠1=∠2 ∵点 H 是边 BC 的中点，∴BH=CH 又∵∠3=∠4 ∴△BEH≌△CFH （2）当 BH=EH 时，四边形 BFCE 是矩形. 理由如下： ∵△BEH≌△CFH ∴BH=CH，EH=FH ∴四边形 BFCE 是平行四边形 又∵BH=EH ∴EF=BC ∴四边形 BFCE 是矩形 H A D CB E F 4 3 21 H A D CB E F 1 2.5 BE AE = 20 1 2.5AE = CF DF 20 3 3DF = 20 3 11.53 ≈ 29. （2014 四川省巴中市，29，10 分） 如图 11，已知△ABC 中，AD 是 BC 边上的中线，以 AB 为直经的⊙O 交 BC 于点 D，过 D 作 MN⊥AC 于点 M，交 AB 的延长线于点 N，过点 B 作 BG⊥MN 于 G. (1) 求证：△BGD∽△DMA；（5 分） (2) 求证：直线 MN 是⊙O 的切线. (5 分) 【答案】解：（1）∵MN⊥AC 于点 M，BG⊥MN 于 G. ∴∠BGD=∠AMD=90° ∴∠DAM+∠ADM=90° ∵AB 为⊙O 的直经 ∴∠ADB=90° ∴∠BDG+∠ADM=90° ∴∠BDG=∠DAM ∴△BGD∽△DMA (2) 连接 OD ∵AD 是 BC 边上的中线，且∠ADB=90° ∴∠1=∠3 4 3 21 H A D CB E F 图11 G M N O B D A C 图11 G M N O B D A C 又∵OA=OD ∴∠1=∠2 ∴OD∥AC ∴∠ODN=∠AMD=90° ∴OD⊥MN ∴直线 MN 是⊙O 的切线. 七、函数的综合运用（本题 10 分） 30.（2014 四川省巴中市，30，10 分） 如图 12, 在平面直角坐标系 xoy 中，已知四边形 DOBC 是矩形，且 D（0,4），B（6,0），若 反比例函数 （x>0）的图像经过线段 OC 的中点 A，交 DC 于点 E，交 BC 于点 F， 设直线 EF 的解析式为 （1）求反比例函数和直线 EF 的解析式；(5 分) （2）求△OEF 的面积；(3 分) （3）请结合图像直接写出不等式 的解集. (2 分) 【答案】解：(1)∵ D（0,4），B（6,0）∴C（6,4） ∵点 A 为线段 OC 的中点 ∴A（3,2） 把 A（3,2）代入 ，得：k=6 ∴ ∴E（ ,4），F（6,1） 1 3 2 G M N O B D A C y x 图12 F E C A B D O 1ky x = 2y k x b= + 1 2 0kk x b x + − > 1ky x = 6y x = 3 2 把 E（ ,4），F（6,1）代入直线 EF 的解析式 得： 解得： ，b=5 ∴ （2）过点 E 作 EG⊥OB 于点 G ∵点 E、F 都在反比例函数图像上 ∴ ∴ ∵E（ ,4），F（6,1） ∴EG=4，FB=1，BG= ∴ (3) 八、综合运用（本题 12 分） 31. （2014 四川省巴中市，31，12 分） 如图 13，在平面直角坐标系 xoy 中，抛物线 与 x 轴交于点 A（-2,0）和点 B，与 y 轴交于点 C，直线 x=1 是该抛物线的对称轴. （1）求抛物线的解析式；(5 分) （2）若两动点 M、H 分别从点 A、B 以每秒 1 个单位长度的速度沿 x 轴同时出发相向而行， y x F E C A B D O G 3 2 2y k x b= + 2 2 3 42 6 1 k b k b  + =  + = 2 2 3k = − 2 53y x= − + OEG OBFS S=   OEF EFBGS S=  梯形 3 2 9 2 ( )1 9 451 42 2 4OEF EFBGS S= = × + × =  梯形 3 62 x< < 2 4y ax bx= + − 当点 M 到达原点时，点 H 立刻掉头，并以每秒 个单位长度的速度向点 B 方向移动，当 点 M 到达抛物线的对称轴时，两点停止运动，经过点 M 的直线 l⊥x 轴，交 AC 或 BC 于 点 P，设点 M 的运动时间为 t 秒（t >0）. 求点 M 的运动时间 t 与△APH 的面积 S 的函数 关系式，并求出 S 的最大值. (7 分) 【答案】解：（1）∵A（-2,0）且直线 x=1 是该抛物线的对称轴 ∴B（4,0） 把 A（-2,0），B（4,0）代入 得： 解得： ∴ （2）∵A（-2,0），C（0,-4） ∴ ①当 0