中考数学动点问题专题练习含答案 21页

动点专题 一、应用勾股定理建立函数解析式 例 1(2000 年·上海)如图 1,在半径为 6,圆心角为 90°的扇形 OAB 的弧 AB 上,有一个动点 P,PH⊥OA, 垂足为 H,△OPH 的重心为 G. (1)当点 P 在弧 AB 上运动时,线段 GO、GP、GH 中,有无长度保持不变的线段?如果有,请指出这样的线 段,并求出相应的长度. (2)设 PH x ,GP y ,求 y 关于 x 的函数解析式，并写出函数的定义域(即自变量 x 的取值范围). (3)如果△PGH 是等腰三角形,试求出线段 PH 的长. 二、应用比例式建立函数解析式 例 2（2006 年·山东）如图 2,在△ABC 中,AB=AC=1,点 D,E 在直线 BC 上运动.设 BD= ,x CE= y . (1)如果∠BAC=30°,∠DAE=105°,试确定 y 与 x 之间的函数解析式； (2)如果∠BAC 的度数为 ,∠DAE 的度数为  ,当 ,  满足怎样的关系式时,(1)中 y 与 x 之间的函 数解析式还成立?试说明理由. 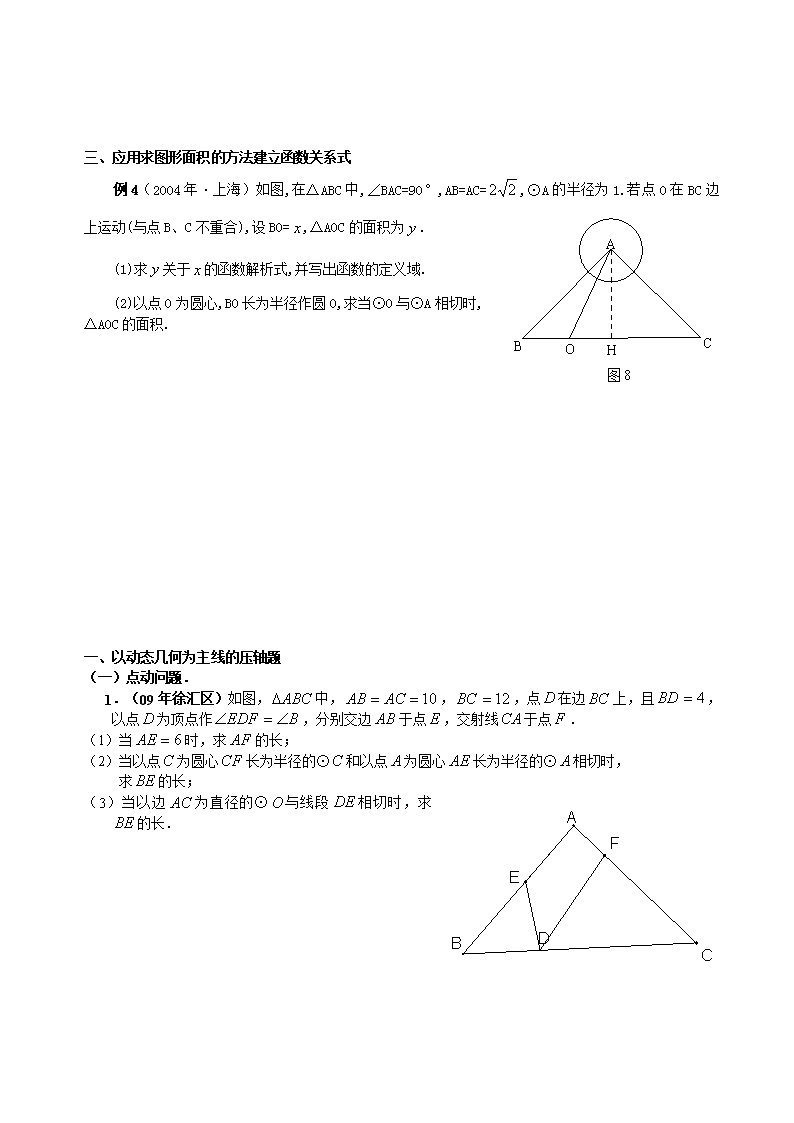A ED CB 图 2 HM N G P O A B 图 1 xy F A B C E D 三、应用求图形面积的方法建立函数关系式 例 4（2004 年·上海）如图,在△ABC 中,∠BAC=90°,AB=AC= 22 ,⊙A 的半径为 1.若点 O 在 BC 边上 运动(与点 B、C 不重合),设 BO= x ,△AOC 的面积为 y . (1)求 y 关于 x 的函数解析式,并写出函数的定义域. (2)以点 O 为圆心,BO 长为半径作圆 O,求当⊙O 与⊙A 相切时, △AOC 的面积. 一、以动态几何为主线的压轴题 （一）点动问题． 1．（09 年徐汇区）如图， ABC 中， 10 ACAB ， 12BC ，点 D 在边 BC 上，且 4BD ， 以点 D 为顶点作 BEDF  ，分别交边 AB 于点 E ，交射线CA 于点 F ． （1）当 6AE 时，求 AF 的长； （2）当以点C 为圆心 CF 长为半径的⊙C 和以点 A 为圆心 AE 长为半径的⊙ A 相切时， 求 BE 的长； （3）当以边 AC 为直径的⊙O 与线段 DE 相切时，求 BE 的长． A B CO 图 8 H A B C DE O l A′ （二）线动问题 2,在矩形 ABCD 中，AB＝3，点 O 在对角线 AC 上，直线 l 过点 O，且与 AC 垂直交 AD 于点 E.(1)若 直线 l 过点 B，把△ABE 沿直线 l 翻折，点 A 与矩形 ABCD 的对称中心 A＇重合，求 BC 的长； (2)若直线 l 与 AB 相交于点 F，且 AO＝ 4 1 AC，设 AD 的长为 x ，五边 形 BCDEF 的面积为 S.①求 S 关于 x 的函数关系式，并指出 x 的取值范 围； ②探索：是否存在这样的 x ，以 A 为圆心，以 x 4 3 长为半径的圆与 直线 l 相切，若存在，请求出 x 的值；若不存在，请说明理由． （三）面动问题 3.如图，在 ABC 中， 6,5  BCACAB ， D 、 E 分别是边 AB 、 AC 上 的两个动点（ D 不与 A 、 B 重合），且保持 BCDE∥ ，以 DE 为边，在点 A 的异侧作正方形 DEFG . （1）试求 ABC 的面积； （2）当边 FG 与 BC 重合时，求正方形 DEFG 的边长； （3）设 xAD  ， ABC 与正方形 DEFG 重叠部分的面积为 y ，试求 y 关 于 x 的函数关系式，并写出定义域； （4）当 BDG 是等腰三角形时，请直接写出 AD 的长． F G E C A B D 解决动态几何问题的常见方法有: 一、 特殊探路，一般推证 例 2：（2004 年广州市中考题第 11 题）如图，⊙O1 和⊙O2 内切于 A， ⊙O1 的半径为 3，⊙O2 的半径为 2，点 P 为⊙O1 上的任一点（与点 A 不重合），直线 PA 交⊙O2 于点 C，PB 切⊙O2 于点 B，则 PC BP 的值为 （A） 2 （B） 3 （C） 2 3 （D） 2 6 二、 动手实践，操作确认 例 4（2003 年广州市中考试题）在⊙O 中，C 为弧 AB 的中点，D 为弧 AC 上任一点（与 A、C 不重 合），则 （A）AC+CB=AD+DB (B) AC+CBAD+DB (D) AC+CB 与 AD+DB 的大小关系不确定 例 5：如图，过两同心圆的小圆上任一点 C 分别作小圆的直径 CA 和非直径的弦 CD，延长 CA 和 CD 与大圆分别交于点 B、E，则下列结论中正确的是（ * ） （A） ABDE  （B） ABDE  （C） ABDE  （D） ABDE, 的大小不确定 三、 建立联系，计算说明 例 6：如图，正方形 ABCD 的边长为 4，点 M 在边 DC 上，且 DM=1， N 为对角线 AC 上任意一点，则 DN+MN 的最小值为 . C O 1 O 2 P B A E D C B A O M N D C B A 以圆为载体的动点问题 例 1. 在 Rt ABC 中，AC＝5，BC＝12，∠ACB＝90°，P 是 AB 边上的动点（与点 A、B 不重合）， Q 是 BC 边上的动点（与点 B、C 不重合），当 PQ 与 AC 不平行时，△CPQ 可能为直角三角形吗？若有可能， 请求出线段 CQ 的长的取值范围；若不可能，请说明理由。（03 年广州市中考） 例 2. 如图 2，直角梯形 ABCD 中，AD∥BC，∠B＝90°，AD＋BC＜DC，若腰 DC 上有动点 P，使 AP⊥ BP，则这样的点有多少个？ 练习. 1 已知，在矩形 ABCD 中，AB=4，BC=2，点 M 为边 BC 的中点，点 P 为边 CD 上的动点（点 P 异于 C、D 两 点）。连接 PM，过点 P 作 PM 的垂线与射线 DA 相交于点 E（如图）。设 CP=x，DE=y。 （1）写出 y 与 x 之间的函数关系式 ； （2）若点 E 与点 A 重合，则 x 的值为 ； （3）是否存在点 P，使得点 D 关于直线 PE 的对称点 D′落在边 AB 上？若存在，求 x 的值；若不存在， 请说明理由。 2 如图，在矩形 ABCD 中，AB=8，AD=6，点 P、Q 分别是 AB 边和 CD 边上的动点，点 P 从点 A 向点 B 运动，点 Q 从点 C 向点 D 运动，且保持 AP-CQ。设 AP= x （1）当 PQ∥AD 时，求 x 的值； （2）当线段 PQ 的垂直平分线与 BC 边相交时，求 x 的取值范围； （3）当线段 PQ 的垂直平分线与 BC 相交时，设交点为 E，连接 EP、EQ，设△EPQ 的面积为 S，求 S 关 于 x 的函数关系式，并写出 S 的取值范围。 3、在平面直角坐标系 XOY 中，一次函数 的图象是直线 l1，l1 与 x 轴、y 轴分别相交于 A、 B 两点．直线 l2 过点 C（a，0）且与直线 l1 垂直，其中 a＞0．点 P、Q 同时从 A 点出发，其中点 P 沿射 线 AB 运动，速度为每秒 4 个单位；点 Q 沿射线 AO 运动，速度为每秒 5 个单位． （1）写出 A 点的坐标和 AB 的长； （2）当点 P、Q 运动了多少秒时，以点 Q 为圆心，PQ 为半径的⊙Q 与直线 l2、y 轴都相切，求此时 a 的 值． 考点：一次函数综合题；切线的性质；相似三角形的判定与性质。 专题：几何动点问题；分类讨论。 分析：（1）根据一次函数图象与坐标轴的交点求法，分别求出坐标即可； （2）根据相似三角形的判定得出 △ APQ∽△AOB，以及当⊙Q 在 y 轴右侧与 y 轴相切时，当⊙Q 在 y 轴 的左侧与 y 轴相切时，分别分析得出答案． 例题 4 如图 1，已知抛物线的顶点为 A（2，1），且经过原点 O，与 x 轴的另一个交点为 B。 ⑴求抛物线的解析式；（用顶点式求得抛物线的解析式为 xx4 1y 2  ） ⑵若点 C 在抛物线的对称轴上，点 D 在抛物线上，且以 O、C、D、B 四点为顶点的四边形为平行四 边形，求 D 点的坐标； ⑶连接 OA、AB，如图 2，在 x 轴下方的抛物线上是否存在点 P，使得△OBP 与△OAB 相似？若存 在，求出 P 点的坐标；若不存在，说明理由。 例 1 题图图 1 图 2 练习 5、已知抛物线 2y ax bx c   经过 5 3( 3 3) 02P E       ，， ， 及原点 (0 0)O ， ． （1）求抛物线的解析式．（由一般式．．．得抛物线的解析式为 22 5 3 3 3y x x   ） （2）过 P 点作平行于 x 轴的直线 PC 交 y 轴于C 点，在抛物线对称轴右侧且位于直线 PC 下方的抛 物线上，任取一点Q ，过点Q 作直线QA 平行于 y 轴交 x 轴于 A 点，交直线 PC 于 B 点，直线QA 与直 线 PC 及两坐标轴围成矩形OABC ．是否存在点 Q ，使得 OPC△ 与 PQB△ 相似？若存在，求出Q 点 的坐标；若不存在，说明理由． （3）如果符合（2）中的Q 点在 x 轴的上方，连结OQ ，矩形 OABC 内的四个三角形 OPC PQB OQP OQA， ， ，△ △ △ △ 之间存在 怎样的关系？为什么？ 练习 6、如图，四边形 OABC 是一张放在平面直角坐标系中的矩形纸片，点 A 在 x 轴上，点 C 在 y 轴上， 将边 BC 折叠，使点 B 落在边 OA 的点 D 处。已知折叠 5 5CE  ，且 3tan 4EDA  。 （1）判断 OCD△ 与 ADE△ 是否相似？请说明理由； （2）求直线 CE 与 x 轴交点 P 的坐标； （3）是否存在过点 D 的直线 l，使直线 l、直线 CE 与 x 轴所围成的 三角形和直线 l、直线 CE 与 y 轴所围成的三角形相似？如果存在，请直 接写出其解析式并画出相应的直线；如果不存在，请说明理由。 O x y 练习 2 图 C B E D A 练习 7、在平面直角坐标系 xOy 中，已知二次函数 2 ( 0)y ax bx c a    的图象与 x 轴交于 A B， 两 点（点 A 在点 B 的左边），与 y 轴交于点C ，其顶点的横坐标为 1，且过点 (2 3)， 和 ( 3 12) ， ． （1）求此二次函数的表达式；（由一般式．．．得抛物线的解析式为 2 2 3y x x    ） （2）若直线 : ( 0)l y kx k  与线段 BC 交于点 D（不与点 B C， 重合），则是否存在这样的直线l ， 使得以 B O D， ， 为顶点的三角形与 BAC△ 相似？若存在，求出该直线的函数表达式及点 D 的坐标；若 不存在，请说明理由； ( 1 0) (3 0), (0 3)A B C ，， ， ， （3）若点 P 是位于该二次函数对称轴右边图象上不与顶点重合的任意一点，试比较锐角 PCO 与 ACO 的大小（不必证明），并写出此时点 P 的横坐标 px 的取值范围． O y C lx BA 1x  练习 3 图 练习 8 (2008 广东湛江市) 如图所示，已知抛物线 2 1y x  与 x 轴交于 A、B 两点，与 y 轴交于点 C． （1）求 A、B、C 三点的坐标． （2）过点 A 作 AP∥CB 交抛物线于点 P，求四边形 ACBP 的面积． （3）在 x 轴上方的抛物线上是否存在一点 M，过 M 作 MG  x 轴于点 G，使以 A、M、G 三点为顶点 的三角形与  PCA 相似．若存在，请求出 M 点的坐标；否则，请说明理由． o C BA x 练习 4 图 P y 练习 9、已知：如图，在平面直角坐标系中， ABC△ 是直角三角形， 90ACB   ，点 A C， 的坐标分 别为 ( 3 0)A  ， ， (1 0)C ， ， 3tan 4BAC  ． （1）求过点 A B， 的直线的函数表达式；点 ( 3 0)A  ， ， (1 0)C ， ， B (13)， ， 3 9 4 4y x  （2）在 x 轴上找一点 D ，连接 DB ，使得 ADB△ 与 ABC△ 相似（不 包括全等），并求点 D 的坐标； （3）在（2）的条件下，如 P Q， 分别是 AB 和 AD 上的动点，连接 PQ ，设 AP DQ m  ，问是否存在这样的 m 使得 APQ△ 与 ADB△ 相似，如存在，请求出 m 的值；如不存在，请说明理由． A CO B x y 例 10 (2008 福建福州)如图，已知△ABC 是边长为 6cm 的等边三角形，动点 P、Q 同时从 A、B 两点 出发，分别沿 AB、BC 匀速运动，其中点 P 运动的速度是 1cm/s，点 Q 运动的速度是 2cm/s，当点 Q 到达 点 C 时，P、Q 两点都停止运动，设运动时间为 t（s），解答下列问题： （1）当 t＝2 时，判断△BPQ 的形状，并说明理由； （2）设△BPQ 的面积为 S（cm2），求 S 与 t 的函数关系式； （3）作 QR//BA 交 AC 于点 R，连结 PR，当 t 为何值时，△APR∽△PRQ？ 分析:由 t＝2 求出 BP 与 BQ 的长度,从而可得△BPQ 的形状; 作 QE⊥BP 于点 E,将 PB,QE 用 t 表示,由 BPQS  = 2 1 ×BP×QE 可得 S 与 t 的函数关系式;先证得四边形 EPRQ 为平行四边形,得 PR=QE, 再由△APR∽△PRQ,对应边成比例列方程,从而 t 值可求. 例 11(2008 浙江温州)如图，在 Rt ABC△ 中， 90A   ， 6AB  ， 8AC  ，D E， 分别是边 AB AC， 的中点，点 P 从点 D 出发沿 DE 方向运动，过点 P 作 PQ BC 于Q ，过点 Q 作QR BA∥ 交 AC 于 R ， 当点Q 与点C 重合时，点 P 停止运动．设 BQ x ，QR y ．（1）求点 D 到 BC 的距离 DH 的长； （2）求 y 关于 x 的函数关系式（不要求写出自变量的取值范围）； （3）是否存在点 P ，使 PQR△ 为等腰三角形？若存在，请求出所有 满足要求的 x 的值；若不存在，请说明理由． 分析:由△BHD∽△BAC,可得 DH;由△RQC∽△ABC,可得 y 关于 x 的函数关系式;由腰相等列方程可得 x 的值;注意需分类讨论. 中考动点专题答案 一、应用勾股定理建立函数解析式 1.解:(1)当点 P 在弧 AB 上运动时,OP 保持不变,于是线段 GO、GP、GH 中,有长度保持不变的线段，这条线段是 GH= 3 2 NH= 2 1 3 2  OP=2. (2)在 Rt△POH 中, 222 36 xPHOPOH  , ∴ 2362 1 2 1 xOHMH  . 在 Rt△MPH 中, . ∴ y =GP= 3 2 MP= 23363 1 x (0< x <6). (3)△PGH 是等腰三角形有三种可能情况: ①GP=PH 时, xx  23363 1 ,解得 6x . 经检验, 6x 是原方程的根,且符合题意. ②GP=GH 时, 23363 1 2  x ,解得 0x . 经检验, 0x 是原方程的根,但不符合题意. ③PH=GH 时, 2x . 综上所述,如果△PGH 是等腰三角形,那么线段 PH 的长为 6 或 2. 二、应用比例式建立函数解析式 2.解:(1)在△ABC 中,∵AB=AC,∠BAC=30°, ∴∠ABC=∠ACB=75°, ∴∠ABD=∠ACE=105°. ∵∠BAC=30°,∠DAE=105°, ∴∠DAB+∠CAE=75°, 又∠DAB+∠ADB=∠ABC=75°, ∴∠CAE=∠ADB, ∴△ADB∽△EAC, ∴ AC BD CE AB  , ∴ 1 1 x y  , ∴ xy 1 . (2)由于∠DAB+∠CAE=   ,又∠DAB+∠ADB=∠ABC= 290  ,且函数关系式成立, ∴ 290  =   , 整理得  2  90 .当  2  90 时,函数解析式 xy 1 成立. 三、应用求图形面积的方法建立函数关系式 例 4 解:(1)过点 A 作 AH⊥BC,垂足为 H. ∵∠BAC=90°,AB=AC= 22 , ∴BC=4,AH= 2 1 BC=2. ∴OC=4- x . ∵ AHOCS AOC  2 1 , ∴ 4 xy ( 40  x ). (2)①当⊙O 与⊙A 外切时, 在 Rt△AOH 中,OA= 1x ,OH= x2 , ∴ 222 )2(2)1( xx  . 解得 6 7x . 22222 3362 1 4 19 xxxMHPHMP  A ED CB 图 2 F A B C E D A B C DE O l A′ 此时,△AOC 的面积 y = 6 17 6 74  . ②当⊙O 与⊙A 内切时, 在 Rt△AOH 中,OA= 1x ,OH= 2x , ∴ 222 )2(2)1(  xx . 解得 2 7x . 此时,△AOC 的面积 y = 2 1 2 74  .综上所述,当⊙O 与⊙A 相切时,△AOC 的面积为 6 17 或 2 1 . 专题二：动态几何型压轴题 一、以动态几何为主线的压轴题 （一）点动问题． 1.解：（1） 证明 CDF ∽ EBD ∴ BE CD BD CF  ，代入数据得 8CF ，∴AF=2 （2） 设 BE= x ,则 ,10 ACd ,10 xAE  利用（1）的 方法 xCF 32 ， 相切时分外切和内切两种情况考虑： 外切， xx 321010  ， 24x ； 内切， xx 321010  ， 17210 x ． 100  x ∴当⊙ C 和⊙ A 相切时， BE 的长为 24 或 17210  ． （3）当以边 AC 为直径的⊙ O 与线段 DE 相切时， 3 20BE ． （二）线动问题 [ 略解] (1)∵A’是矩形 ABCD 的对称中心∴A’B＝AA’＝ 2 1 AC ∵AB＝A’B，AB＝3∴AC＝6 33BC (2) ① 92  xAC ， 94 1 2  xAO ， )9(12 1 2  xAF ， x xAE 4 92  ∴ AF2 1  AES AEF x x 96 )9( 22  ， x xxS 96 )9(3 22  x xx 96 81270 24  ( 333  x ) ②若圆 A 与直线 l 相切，则 94 1 4 3 2  xx ， 01 x (舍去)， 5 8 2 x ∵ 35 8 2 x ∴不存在这样的 x ， 使圆 A 与直线 l 相切． 练习 1. 解： （1）y=－x2＋4x。 （2）2+ 2或。2－ 2 （3）存在。 过点 P 作 PH⊥AB 于点 H。则 ∵点 D 关于直线 PE 的对称点 D′落在边 AB 上， ∴P D′=PD=4－x，E D′=ED= y=－x2＋4x，EA=AD－ED= x2－4x＋2，∠P D′E=∠D=900。 在 Rt△D′P H 中，PH=2， D′P =DP=4－x，D′H= (4－x)²－2²= x²－8x+12。 ∵∠ E D′A=1800－900－∠P D′H=900－∠P D′H=∠D′P H，∠P D′E=∠P HD′ =900， ∴△E D′A∽△D′P H。∴ED′ D′P = EA D′H ，即-x²+4x 4-x = x²-4x+2 x²－8x+12 ， 即x= x²-4x+2 x²－8x+12 ，两边平方并整理得，2x2－4x＋1=0。解得 x=2± 2 2 。 ∵当x=2+ 2 2 时，y=- 2+ 2 2 ²+4×2+ 2 2 = 5+2 2 2 ＞ 2. ∴此时，点 E 已在边 DA 延长线上，不合题意，舍去（实际上是无理方程的增根）。 ∵当x=2- 2 2 时，y=- 2- 2 2 ²+4×2- 2 2 = 5-2 2 2 ＜2. ∴此时，点 E 在边 AD 上，符合题意。 ∴当x=2- 2 2 时，点 D 关于直线 PE 的对称点 D′落在边 AB 上。 法二 三角形 DAD’相似三角形 PDE. ED’= 表达式 ； AD’=表达式，利用勾股定理 2 .解：（1）当 PQ∥AD 时，x＝4. （2）如图，连接 EP、EQ，则 EP＝EQ，设 BE＝y， ∴ 2222 )6()8( xyyx  得 3 74  xy ∵0≤y≤6 ∴0≤ 3 74 x ≤6 ∴ 4 7 ≤x≤ 4 25 （3） 6 56394)8(3 74 2 1 2 1 2  xxxxBPBES BPE 6 254)3 746(2 1 2 1 2 xxxxCQCES ECQ  由题意 ∵AP＝CQ，∴ 24S2 1 ABCDBPQC  矩形梯形S ∴ 6 x25x4 6 56x39x424SSS 22 BPEBPQC  梯形 整理得： ）（）（ 4 25x4 7124x3 4 3 100x32x4S 2 2  当 x＝4 时，S 有最小值 12. 当 x＝ 4 7 或 x＝ 4 25 时，S 有最大值 4 75 ∴12≤S≤ 4 75 【涉及知识点】动点问题，方程，勾股定理，三角形的面积，梯形的面积 【点评】本题主要考查学生对动点问题的理解掌握情况。第一个问题要求学生能够根据问题列出符 合题意的方程，在第二个问题中，学生必须利用边的相等关系，再利用勾股定理求出 x 的取值范围，第 三个问题根据面积关系列出函数关系式，进而取出 S 的取值，本题难度较大． 3 在平面直角坐标系 XOY 中，一次函数 的图象是直线 l1，l1 与 x 轴、y 轴分别相交于 A、B 两点．直线 l2 过点 C（a，0）且与直线 l1 垂直，其中 a＞0．点 P、Q 同时从 A 点出发，其中点 P 沿射线 AB 运动，速度为每秒 4 个单位；点 Q 沿射线 AO 运动，速度为每秒 5 个单位． （1）写出 A 点的坐标和 AB 的长； （2）当点 P、Q 运动了多少秒时，以点 Q 为圆心，PQ 为半径的⊙Q 与直线 l2、y 轴都相切，求此时 a 的 值． 考点：一次函数综合题；切线的性质；相似三角形的判定与性质。 专题：几何动点问题；分类讨论。 分析：（1）根据一次函数图象与坐标轴的交点求法，分别求出坐标即可； （2）根据相似三角形的判定得出 △ APQ∽△AOB，以及当⊙Q 在 y 轴右侧与 y 轴相切时，当⊙Q 在 y 轴 的左侧与 y 轴相切时，分别分析得出答案． 解答：解：（1）∵一次函数 的图象是直线 l1，l1 与 x 轴、y 轴分别相交于 A、B 两点， ∴y=0 时，x=﹣4， ∴A（﹣4，0），AO=4， ∵图象与 y 轴交点坐标为：（0，3），BO=3， ∴AB=5； （2）由题意得：AP=4t，AQ=5t， = =t， 又∠PAQ=∠OAB， ∴△APQ∽△AOB， ∴∠APQ=∠AOB=90°， ∵点 P 在 l1 上， ∴⊙Q 在运动过程中保持与 l1 相切，（没发掘这一条件） ①当⊙Q 在 y 轴右侧与 y 轴相切时，设 l2 与⊙Q 相切于 F，由 △ APQ∽△AOB，得： ∴ ， ∴PQ=6； 连接 QF，则 QF=PQ，由 △ QFC∽△APQ∽△AOB， 得： ， ∴ ， ∴ ， ∴QC= ， ∴a=OQ+QC= ， ②当⊙Q 在 y 轴的左侧与 y 轴相切时，设 l2 与⊙Q 相切于 E，由 △ APQ∽△AOB 得： = ， ∴PQ= ， 连接 QE，则 QE=PQ，由 △ QEC∽△APQ∽△AOB 得： = ， ∴ ， = ， ∴QC= ，a=QC﹣OQ= ， ∴a 的值为 和 ， 点评：此题主要考查了切线的性质以及相似三角形的判定与性质，利用数形结合进行分析注意分类讨论 才能得出正确答案．