2011——2016年河南中考数学第22题解析 8页

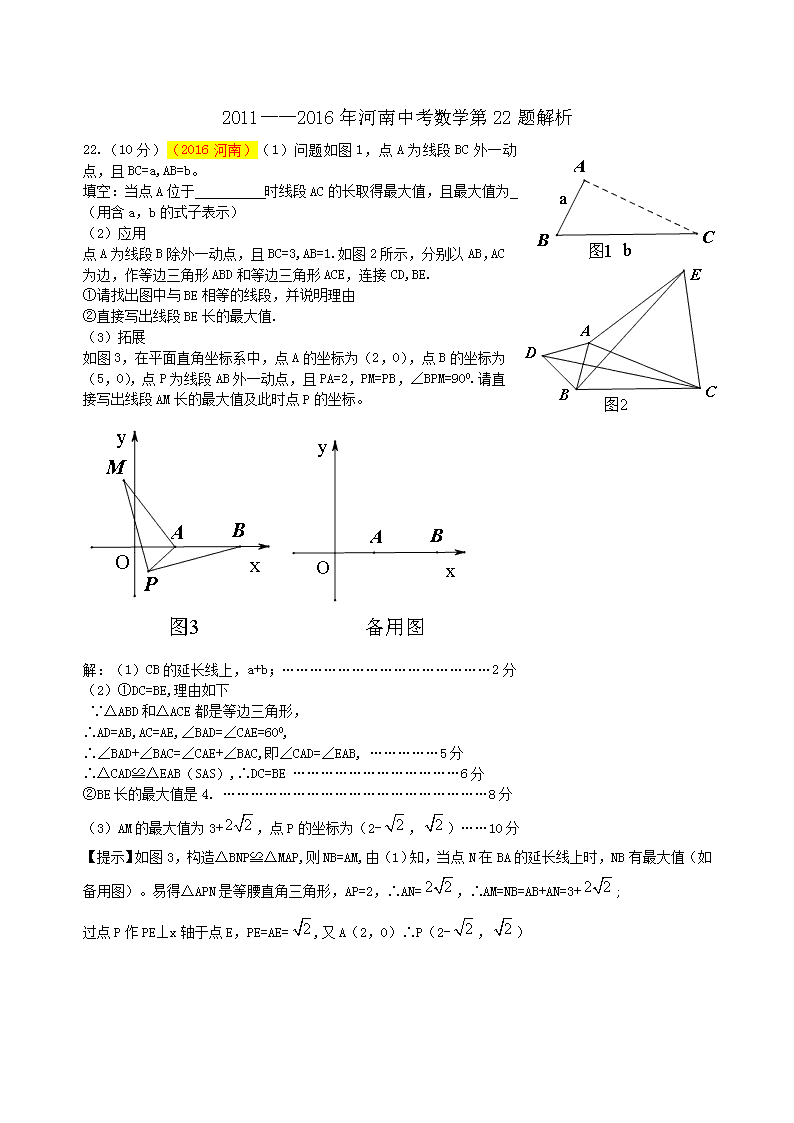
‎2011——2016年河南中考数学第22题解析 ‎22.（10分）（2016河南）（1）问题如图1，点A为线段BC外一动点，且BC=a,AB=b。‎ 填空：当点A位于 时线段AC的长取得最大值，且最大值为 ‎ ‎（用含a，b的式子表示）‎ ‎（2）应用 点A为线段B除外一动点，且BC=3,AB=1.如图2所示，分别以AB，AC为边，作等边三角形ABD和等边三角形ACE，连接CD,BE.‎ ‎①请找出图中与BE相等的线段，并说明理由 ‎②直接写出线段BE长的最大值. ‎ ‎（3）拓展 如图3，在平面直角坐标系中，点A的坐标为（2，0），点B的坐标为（5，0），点P为线段AB外一动点，且PA=2，PM=PB，∠BPM=900.请直接写出线段AM长的最大值及此时点P的坐标。‎ ‎ ‎ 解：（1）CB的延长线上，a+b；………………………………………2分 ‎（2）①DC=BE,理由如下 ‎ ∵△ABD和△ACE都是等边三角形，‎ ‎∴AD=AB,AC=AE,∠BAD=∠CAE=600,‎ ‎∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB, ……………5分 ‎∴△CAD≌△EAB（SAS）,∴DC=BE ………………………………6分 ‎②BE长的最大值是4. …………………………………………………8分 ‎（3）AM的最大值为3+，点P的坐标为（2-，）……10分 ‎【提示】如图3，构造△BNP≌△MAP,则NB=AM,由（1）知，当点N在BA的延长线上时，NB有最大值（如备用图）。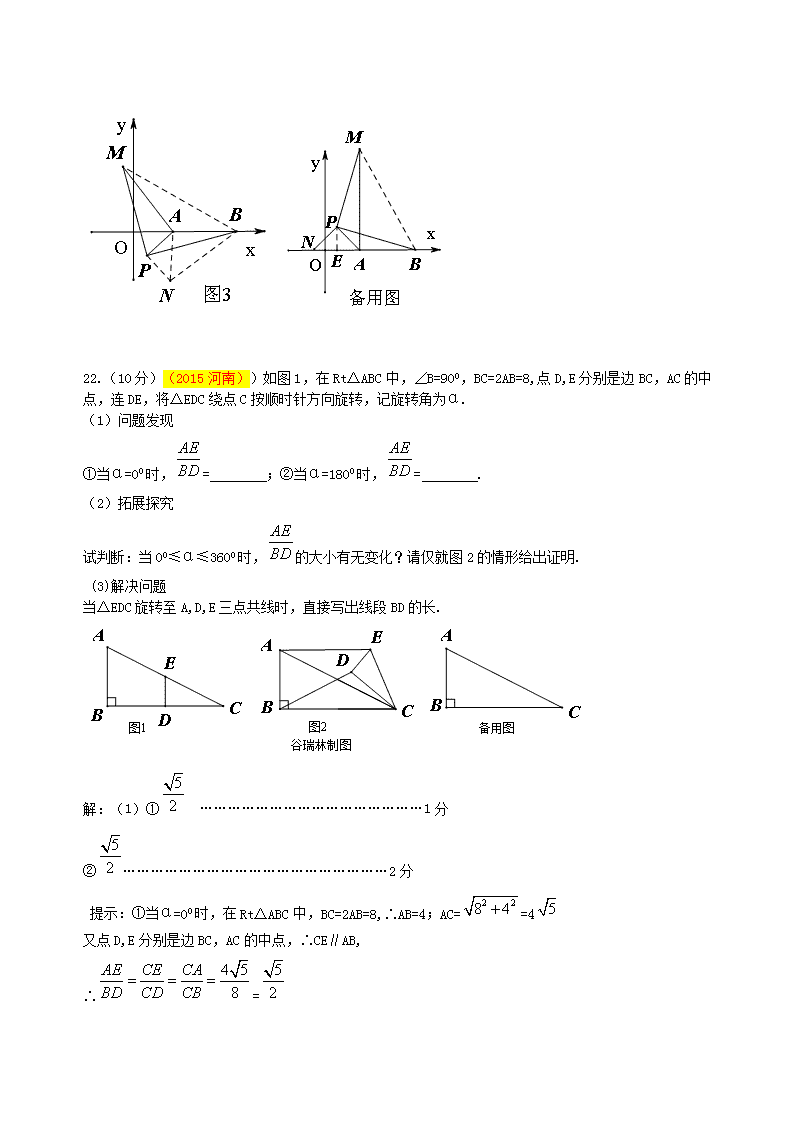易得△APN是等腰直角三角形，AP=2，∴AN=，∴AM=NB=AB+AN=3+;‎ 过点P作PE⊥x轴于点E，PE=AE=,又A（2，0）∴P（2-，）‎ ‎ ‎ ‎22.（10分）（2015河南））如图1，在Rt△ABC中，∠B=900，BC=2AB=8,点D,E分别是边BC，AC的中点，连DE，将△EDC绕点C按顺时针方向旋转，记旋转角为α.‎ ‎（1）问题发现 ‎①当α=00时，= ；②当α=1800时，= .‎ ‎（2）拓展探究 试判断：当00≤α≤3600时，的大小有无变化？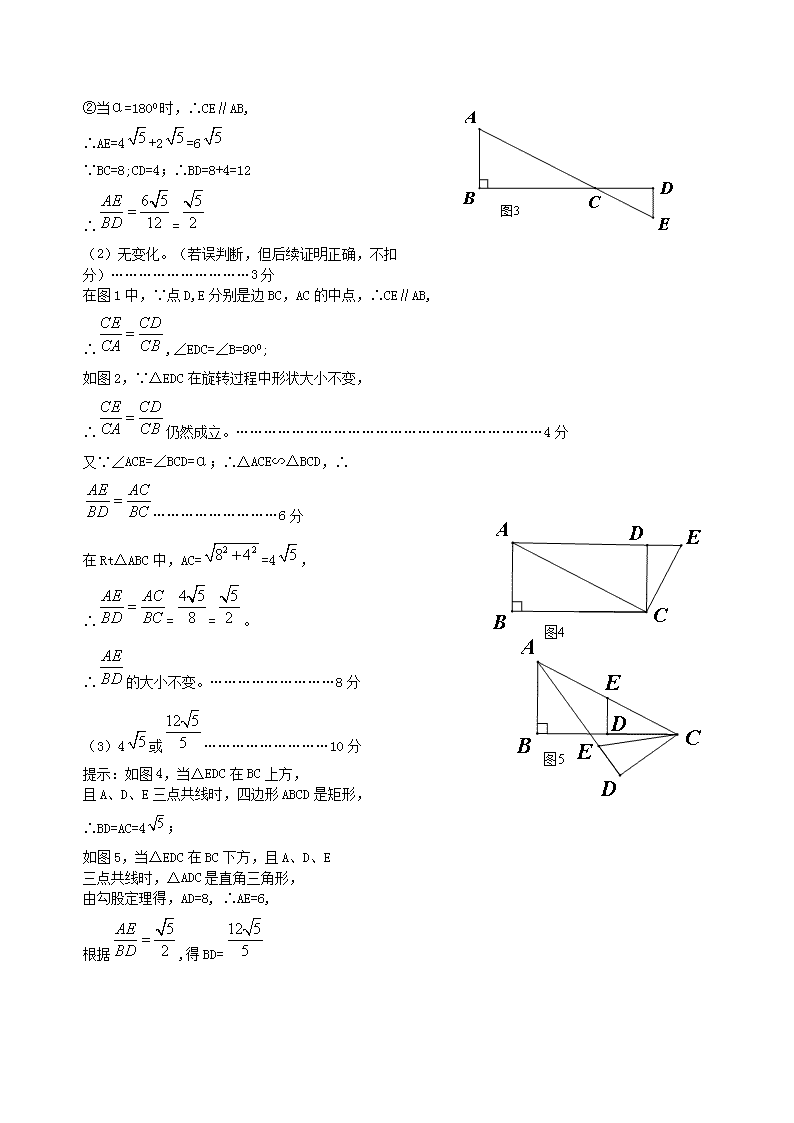请仅就图2的情形给出证明.‎ ‎ (3)解决问题 当△EDC旋转至A,D,E三点共线时，直接写出线段BD的长.‎ 解：（1）① …………………………………………1分 ‎②…………………………………………………2分 ‎ 提示：①当α=00时，在Rt△ABC中，BC=2AB=8,∴AB=4；AC==4‎ 又点D,E分别是边BC，AC的中点，∴CE∥AB, ‎ ‎∴=‎ ‎②当α=1800时，∴CE∥AB,‎ ‎∴AE=4+2=6‎ ‎∵BC=8;CD=4；∴BD=8+4=12‎ ‎∴=‎ ‎（2）无变化。（若误判断，但后续证明正确，不扣分）…………………………3分 在图1中，∵点D,E分别是边BC，AC的中点，∴CE∥AB,‎ ‎∴,∠EDC=∠B=900;‎ 如图2，∵△EDC在旋转过程中形状大小不变，‎ ‎∴仍然成立。…………………………………………………………4分 又∵∠ACE=∠BCD=α；∴△ACE∽△BCD，∴………………………6分 在Rt△ABC中，AC==4，‎ ‎∴==。‎ ‎∴的大小不变。………………………8分 ‎（3）4或………………………10分 提示：如图4，当△EDC在BC上方，‎ 且A、D、E三点共线时，四边形ABCD是矩形，‎ ‎∴BD=AC=4；‎ 如图5，当△EDC在BC下方，且A、D、E 三点共线时，△ADC是直角三角形，‎ 由勾股定理得，AD=8, ∴AE=6,‎ 根据,得BD=‎ ‎22.（10分）（2014河南）（1）问题发现 如图1，△ACB和△DCE均为等边三角形，点A、D、E在同一直线上，连接BE 填空：（1）∠AEB的度数为 ；（2）线段AD、BE之间的数量关系是 。‎ ‎（2）拓展探究 如图2，△ACB和△DCE均为等腰三角形，∠ACB=∠DCE=900, 点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE。请判断∠AEB的度数及线段CM、AE、BE之间的数量关系，并说明理由。‎ （3）解决问题 如图3，在正方形ABCD中，CD=。若点P满足PD=1,且∠BPD=900，请直接写出点A到BP的距离。‎ ‎22. （1）①60；②AD=BE. ……………………………………………………………2分 ‎ ‎（2）∠AEB＝900；AE=2CM+BE. ………………………………………………4分 ‎（注：若未给出本判断结果，但后续理由说明完全正确，不扣分）‎ 理由：∵△ACB和△DCE均为等腰直角三角形，∠ACB =∠DCE= 900,‎ ‎ ∴AC=BC, CD=CE, ∠ACB=∠DCB=∠DCE－∠DCB, 即∠ACD= ∠BCE ‎∴△ACD≌△BCE. ………………………………………………………………6分 ‎∴AD = BE, ∠BEC=∠ADC=1350.‎ ‎ ∴∠AEB=∠BEC－∠CED=1350－450=900．…………………………………7分 ‎ 在等腰直角三角形DCE中，CM为斜边DE上的高，‎ ‎ ∴CM= DM= ME,∴DE=2CM.‎ ‎∴AE=DE+AD=2CM+BE………………………………………………………8分 ‎(3)或…………………………………………………………10分 ‎ 【提示】PD =1，∠BPD=900,‎ ‎ ∴BP是以点D为圆心、以1为半径的OD的切线，点P为切点．‎ ‎ 第一种情况：如图①，过点A作AP的垂线，交BP于点P/，‎ ‎ 可证△APD≌△AP/B,PD=P/B=1,‎ ‎ CD=,∴BD=2,BP=,∴AM=PP/=(PB-BP/)=‎ ‎ 第二种情况如图②，可得AMPP/=(PB+BP/)=‎ ‎22.（10分）（2013河南）如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°，∠B=∠E=30°.‎ ‎（1）操作发现 如图2，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB边上时，填空：‎ ‎①线段DE与AC的位置关系是_________；‎ ‎②设△BDC的面积为S1，△AEC的面积为S2，则S1与S2的数量关系是_________________.‎ ‎（2）猜想论证 M 图3‎ A B C D E N 当△DEC绕点C旋转到图3所示的位置时，小明猜想（1）中S1与S2的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC、CE边上的高，请你证明小明的猜想.‎ A(D)‎ B(E)‎ C 图1‎ A C B D E 图2‎ E C D B A ‎ 图4‎ ‎（3）拓展探究 已知∠ABC=60°，点D是其角平分线上一点，BD=CD=4，DE//AB交BC于点E（如图4）.‎ 若在射线BA上存在点F，使S△DCF=S△BDE，‎ 请直接写出相应的BF的长.‎ ‎【解析】‎ 试题分析：（1）①根据旋转的性质可得AC=CD,然后求出△ACD是等边三角形,根据等边三角形的性质可得∠ACD=60º,然后根据内错角相等,两直线平行解答;②根据等边三角形的性质可得AC=AD,再根据直角三角形30º角所对的直角边等于斜边的一半求出AC=AB,然后求出AC=BD,再根据等边三角形的性质求出点C到AB的距离等于点D到AC的距离,然后根据等底等高的三角形的面积相等解答;‎ ‎(2)根据旋转的性质可得BC=CE,AC=CD,再求出∠ACN=∠DCM,然后利用"角角边"证明△ACN和△DCM全等,根据全等三角形对应边相等可得AN=DM,然后利用等底等高的三角形的面积相等证明;‎ 试题解析：‎ ‎（1）①线段DE与AC的位置关系是平行 ．②S1与S2的数量关系是相等．‎ 证明：如图2，过D作DN⊥AC交AC于点N，过E作EM⊥AC交AC延长线于M，过C作CF⊥AB交AB于点F．‎ 由①可知△ADC是等边三角形，DE∥AC，‎ ‎∴DN=CF,DN=EM．‎ ‎∴CF=EM． 图2‎ ‎∵∠ACB=90º,∠B=30º， ‎ ‎∴AB=2AC．‎ 又∵AD=AC,‎ ‎∴BD=AC．‎ ‎∵S1=CF·BD,S2=AC·EM， 图3 ‎ ‎∴S1=S2．‎ 证明：如图3，作DG⊥BC于点G，AH⊥CE交EC延长线于点H.‎ ‎∵∠DCE=∠ACB=90º∴∠DCG+∠ACE=180º．‎ 又∵∠ACH+∠ACE=180º,∴∠ACH=∠DCG．‎ 又∵∠CHA=∠CGD=90º,AC=CD,‎ ‎∴△AHC≌△DGC．‎ ‎∴AH=DG．·又∵CE=CB,∴S1=S2．‎ 又∵CE=CB,∴S1=S2．‎ ‎（3）如图，过点D作DF1∥BE，易求四边形BEDF1是菱形，所以BE=DF1，且BE、DF1上的高相等，‎ 此时S△DCF=S△BDE，过点D作DF2⊥BD，‎ ‎∵∠ABC=60°，∴∠F1DF2=∠ABC=60°， ∴△DF1F2是等边三角形，∴DF1=DF2，‎ ‎∵BD=CD，∠ABC=60°，点D是角平分线上一点， ∴∠DBC=∠DCB=0.5×60°=30°‎ ‎，∴∠CDF1=180°-30°=150°，∠CDF2=360°-150°-60°=150°， ∴∠CDF1=∠CDF2，∵在△CDF1和△CDF2中，∴△CDF1≌△CDF2（SAS），‎ ‎∴点F2也是所求的点， ∵∠ABC=60°，点D是角平分线上一点，DE∥AB，∴∠DBC=∠BDE=∠ABD=0.×60°=30°， 又∵BD=4，∴BE= ∴BF1= ，BF2=BF1+F1F2= ‎ 故BF的长为或．‎ ‎22.（10分）（2012河南）类比、转化、从特殊到一般等思想方法，在数学学习和研究中经常用到，如下是一个案例，请补充完整．‎ 原题：如图1，在□ABCD中，点E是BC边的中点，点F是线段AE上一点，BF的延长线交射线CD于点G，若，求的值．‎ ‎（1）尝试探究 在图1中，过点E作EH∥AB交BG于点H，则AB和EH的数量关系是_______________，CG和EH的数量关系是_________________，的值是 ．‎ ‎（2）类比延伸 如图2，在原题的条件下，若（m＞0），则的值是 （用含m的代数式表示），试写出解答过程．‎ ‎（3）拓展迁移 如图3，梯形ABCD中，DC∥AB，点E是BC的延长线上一点，AE和BD相交于点F.‎ 若（a＞0，b＞0），则的值是 （用含a、b的代数式表示）．‎ ‎22．（1）AB=3EH；CG=2EH；． （3分）‎ ‎（2）． …………………………（4分）‎ 作EH∥AB交BG于点H，则△EFH∽△AFB．‎ ‎∵AB=CD，∴CD=mEH． …………………...（5分）‎ ‎∵EH∥AB∥CD，∴△BEH∽△BCG． ‎ ‎ ‎ ‎（3）ab．…………………………………………………..（10分）‎ ‎【提示】过点E作EH∥AB交BD的延长线于点H．‎ ‎22.（2011河南）（10分）如图，在Rt△ABC中，∠B=90°，BC=5，∠C=30°‎ ‎.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动.设点D、E运动的时间是t秒（t＞0）.过点D作DF⊥BC于点F，连接DE、EF.‎ ‎（1）求证：AE=DF；‎ ‎（2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由.‎ ‎（3）当t为何值时，△DEF为直角三角形？请说明理由.‎ 解：（1）在△DFC中，∠DFC=90°，∠C=30°，DC=2t，∴DF=t.‎ 又∵AE=t，∴AE=DF.……………2分 ‎（2）能.理由如下：‎ ‎∵AB⊥BC，DF⊥BC，∴AE∥DF.‎ 又AE=DF，∴四边形AEFD为平行四边形.……3分 ‎∵AB=BC·tan30°=‎ 若使为菱形，则需 即当时，四边形AEFD为菱形.…………………………………5分 ‎（3）①∠EDF=90°时，四边形EBFD为矩形. ‎ 在Rt△AED中，∠ADE=∠C=30°，∴AD=2AE.即10-2t=2t，.………7分 ‎②∠DEF=90°时，由（2）知EF∥AD，∴∠ADE=∠DEF=90°.‎ ‎∵∠A=90°-∠C=60°，∴AD=AE·cos60°.‎ 即………………………………………………………9分 ‎③∠EFD=90°时，此种情况不存在.‎ 综上所述，当或4时，△DEF为直角三角形.……………………10分