广安市2010年中考数学卷 6页

广安市二O—O年高中阶段教育学校招生考试 数学试卷 注意事项：1．本试卷共8页，满分150分，考试时间120分钟．‎ ‎ 2．答题前请考生将自己的姓名、考号填涂到机读卡和试卷相应位置上．‎ ‎ 3．请考生将选择题答案填涂在机读卡上，将非选择题直接答在试题卷中．‎ ‎ 4．解答三至六题时要写出必要的文字说明、证明过程或演算步骤．‎ 一、选择题：每小题给出的四个选项中。只有一个选项符合题意要求。请将符合要求的选项的代号填涂在机读卡上。(本大题共10个小题，每小题2分，共20分)‎ ‎1．的绝对值是 ‎ A． B．2 C． D．‎ ‎2．下列计算正确的是 ‎ A． B． C． D． ‎ ‎3．由四个相同的小正方体堆成的物体，如图l所示，它的俯视图是 ‎4．某同学午觉醒来发现钟表停了，他打开收音机想听电台整点报时，则他等待的时间不超过15分钟的概率是 ‎ A． B． C． D．‎ ‎5．等腰三角形的两边长为4、9，则它的周长是 ‎ A．17 B．17或22 C．20 D．22‎ ‎6．玉树地震后，某市人民献爱心为玉树捐人民币：203000000元，这个数用科学记数法表示为 ‎ A． B． C． D．‎ ‎7．如图2，小明在扇形花台OAB沿D路径散步，能近似地刻画小明到出发点O的距离y与时间x之间的函数图象是 ‎8．若，则的值为 ‎ A．8 B． 2 C．5 D．‎ ‎9．下列说法正确的是 ‎ A．为了解全省中学生的心理健康状况，宜采用普查方式 ‎ B．某彩票设“中奖概率为”，购买100张彩票就—定会中奖一次 ‎ C．某地会发生地晨是必然事件 ‎ D．若甲组数据的方差，乙组数据的方差，则甲组数据比乙组稳定 ‎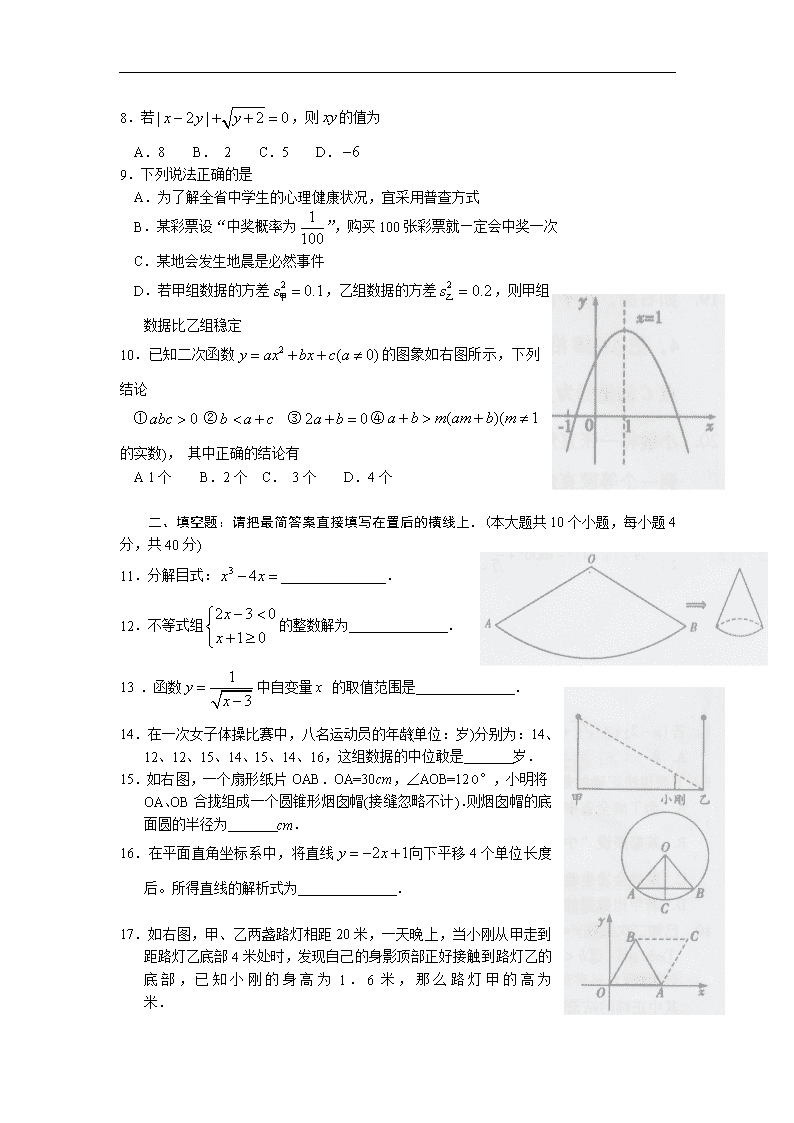10．已知二次函数的图象如右图所示，下列结论 ‎ ① ② ③④的实数)， 其中正确的结论有 ‎ A 1个 B．2个 C． 3个 D．4个 ‎ 二、填空题：请把最简答案直接填写在置后的横线上．(本大题共10个小题，每小题4分，共40分)‎ ‎11．分解目式： ．‎ ‎12．不等式组的整数解为 ．‎ ‎13．函数中自变量x的取值范围是 ．‎ ‎14．在一次女子体操比赛中，八名运动员的年龄(单位：岁)分别为：14、12、12、15、14、15、14、16，这组数据的中位敢是 岁．‎ ‎15．如右图，一个扇形纸片OAB．OA=30cm，∠AOB=120°，小明将OA、OB合拢组成一个圆锥形烟囱帽(接缝忽略不计)．则烟囱帽的底面圆的半径为 cm．‎ ‎16．在平面直角坐标系中，将直线向下平移4个单位长度后。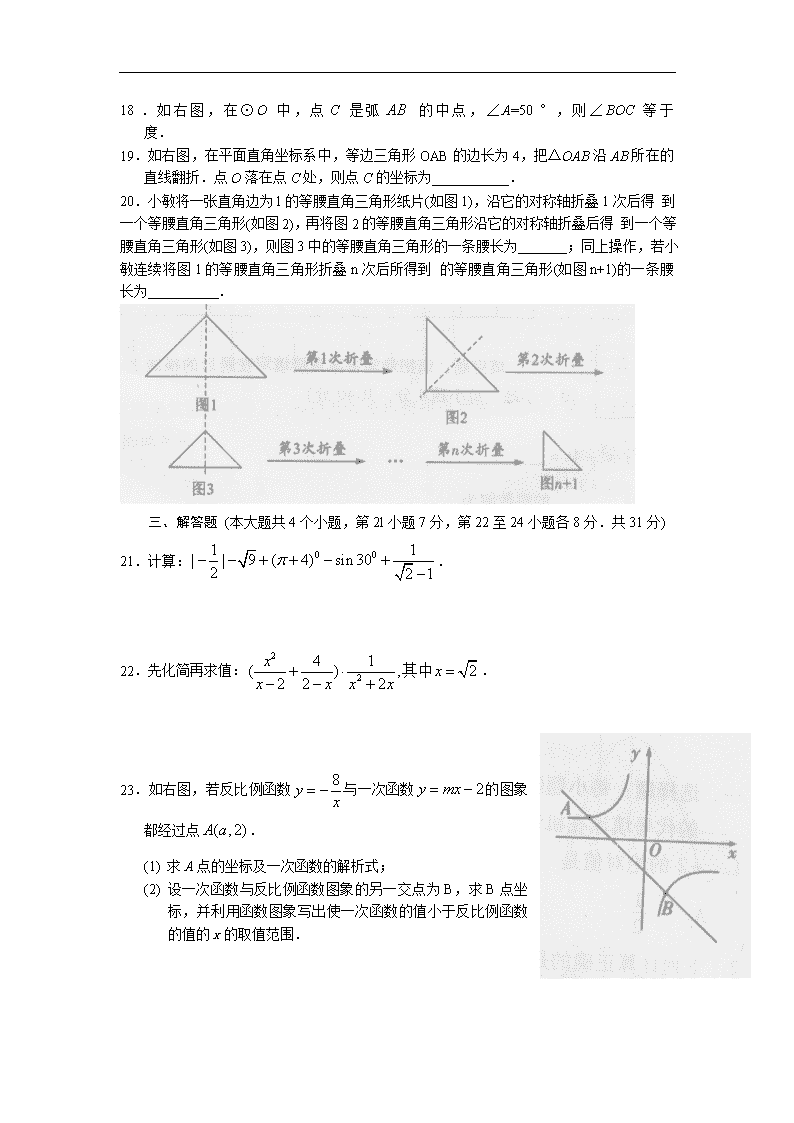所得直线的解析式为 ．‎ ‎17．如右图，甲、乙两盏路灯相距20米，一天晚上，当小刚从甲走到距路灯乙底部4米处时，发现自己的身影顶部正好接触到路灯乙的底部，已知小刚的身高为1．6米，那么路灯甲的高为 米．‎ ‎18．如右图，在⊙O中，点C是弧 的中点，∠A=50°，则∠BOC等于 度．‎ ‎19．如右图，在平面直角坐标系中，等边三角形OAB的边长为4，把△OAB沿AB所在的直线翻折．点O落在点C处，则点C的坐标为 ．‎ ‎20．小敏将一张直角边为l的等腰直角三角形纸片(如图1)，沿它的对称轴折叠1次后得 到一个等腰直角三角形(如图2)，再将图2的等腰直角三角形沿它的对称轴折叠后得 到一个等腰直角三角形(如图3)，则图3中的等腰直角三角形的一条腰长为 ；同上操作，若小敏连续将图1的等腰直角三角形折叠n次后所得到 的等腰直角三角形(如图n+1)的一条腰长为 ．‎ ‎ 三、解答题 (本大题共4个小题，第2l小题7分，第22至24小题各8分．共31分)‎ ‎21．计算：．‎ ‎22．先化简再求值：．‎ ‎23．如右图，若反比例函数与一次函数的图象都经过点．‎ ‎(1) 求A点的坐标及一次函数的解析式；‎ ‎(2) 设一次函数与反比例函数图象的另一交点为B，求B点坐标，并利用函数图象写出使一次函数的值小于反比例函数的值的x的取值范围．‎ ‎24．已知：如右图，在矩形ABCD中，BE=CF，求证：AF=DE．‎ 四、实践应用(本大题共4个小题，其中25、26、27每小题9分，28题10分，共37分)‎ ‎25．某单位需招聘一名技术员，对甲、乙、丙三名候选人进行了笔试和面试两项测试，其成 ‎ 绩如下表所示：‎ 测试项目 测试成绩/分 甲 乙 丙 笔试 ‎80‎ ‎85‎ ‎95‎ 面试 ‎98‎ ‎75‎ ‎73‎ 根据录用程序，该单位又组织了100名评议人员对三人进行投票测评，其得票率如扇形图所示，每票1分(没有弃权票．每人只能投1票)‎ ‎(1) 请算出三人的民主评议得分；‎ ‎(2) 该单位将笔试、面试、民主评议三项测试得分按2：2：1确定综合成绩，谁将被录用请说明理由．‎ ‎26．如图．是一座人行天桥的示意图，天桥的高是l0米，坡面的倾斜角为45°，为了方便行人安全过天桥，市政部门决定降低坡度．使新坡面的倾斜角为30°若新坡脚前需留2 ．5米的人行道，问离原坡脚10米的建筑物是否需要拆除?请说明理由 ‎(参考数据压)‎ ‎27．某学校花台上有一块形如右图所示的三角形ABC地砖，现已破损．管理员要对此地砖 测量后再去市场加工一块形状和大小与此完全相同的地砖来换，今只有尺子和量角器，请你帮他设计一个测量方案，使其加工的地砖能符合要求，并说明理由 ‎28．为了提高土地利用率，将小麦、玉米、黄豆三种农作物套种在一起，俗称“三种三收”，现将面积为l0亩的一块农田进行“三种三收”套种，为保证主要农作物的种植比例．要求小麦的种植面积占总面积的60％，下表是三种农作物的亩产量及销售单价的对应表 小麦 玉米 黄豆 亩产量(千克)‎ ‎400‎ ‎600‎ ‎220‎ 销售单价(元／千克)‎ ‎2‎ ‎1‎ ‎2．5‎ ‎(1) 设玉米的种值面积为x亩，三种农作物的总售价为y元，写出y与x的函数关系式；‎ ‎(2) 在保证小麦种植面积的情况下，玉米、黄豆同时均按整亩数套种，有几种“三种三收”套种方案?‎ ‎(3) 在(2)中的种植方案中，采用哪种套种方案才能使总销售价最高?最高价是多少?‎ 五、推理论证题(本题10分)‎ ‎29．如图，AB、AC分别是⊙O的直径和弦，点D为劣弧AC上一点，弦DE⊥AB分别交⊙O于E，交AB于H，交AC于F．P是ED延长线上一点且PC=PF．‎ ‎ (1) 求证：PC是⊙O的切线；‎ ‎(2) 点D在劣弧AC什么位置时，才能使，为什么?‎ ‎(3) 在(2)的条件下，若OH=1，AH=2，求弦AC的长．‎ 六、拓展探索题(本题12分)‎ ‎30．如图，直线与抛物线都经过点、．‎ ‎（1）求抛物线的解析式；‎ ‎(2) 动点P在线段AC上，过点P作x轴的垂线与抛物线相交于点E，求线段PE长度的最大值；‎ ‎(3) 当线段PE的长度取得最大值时，在抛物线上是否存在点Q，使△PCQ是以PC为直角边的直角三角形?若存在，请求出Q点的坐标；若不存在．请说明理由．‎