2018中考数学专题复习分类讨论经典例题 4页

2018(上)NS 数理推演拓展 11 专题复习（二）分类思想 姓名___________班级___________ 一．基础练习 1．半径为 13 的⊙O 中，弦 AB∥CD，弦 AB 和 CD 的距离为 7，若 AB=24，则 CD 的长为（ ） A．10 B． 304 C．10 或 304 D．10 或 1652 2．若函数 2 1(m 2) 12y mx x m     的图象与 x 轴只有一个交点，那么 m 的值为（ ） A、0 B、0 或 2 C、2 或﹣2 D、0，2 或﹣2 3．如图，在平面直角坐标系 xOy 中，A（0，2），B（0，6），动点 C 在直线 y=x 上．若以 A、 B、C 三点为顶点的三角形是等腰三角形，则点 C 的个数是（ ） A．2 B．3 C．4 D．5 4．如图，矩形 ABCD 中，AB=4，BC= 34 ，点 E 是折线段 A-D-C 上的一个动点（点 E 与点 A 不重合），点 P 是点 A 关于 BE 的对称点．使△PCB 为等腰三角形的点 E 的位置共有（ ） A．2 B．3 C．4 D．5 5．如图在边长为 2 的正方形 ABCD 中，E，F，O 分别是 AB，CD，AD 的中点，以 O 为圆心， 以 OE 为半径画弧 EF．P 是 ⌒ EF 上的一个动点，连接 OP，并延长 OP 交线段 BC 于点 K，过点 P 作⊙O 的切线，分别交射线 AB 于点 M，交直线 BC 于点 G．若 3 BM BG ，则 BK=_______． 6．如图，在 Rt△ABC 中，∠C=90°，∠A=30°，AB＝ 34 ．若动点 D 在线段 AC 上（不与 点 A、C 重合），过点 D 作 DE⊥AC 交 AB 边于点 E． （1）当点 D 运动到线段 AC 中点时，DE=_______； （2）点 A 关于点 D 的对称点为点 F， 以 FC 为半径作⊙C，当 DE= ____________ 时，⊙C 与直线 AB 相切． 7．如图，在平面直角坐标系中，O 为坐标原点，点 A 的坐标为（-8，0），直线 BC 经过点 B （-8，6），C（0，6），将四边形 OABC 绕点 O 按顺时针方向旋转α度（0＜α≤180°）得到四 边形 O′A′B′C′，此时直线 OA′、直线′B′C′分别与直线 BC 相交于 P、Q．在四边形 OABC 旋转 过程中，若 BP= 2 1 BQ，则点 P 的坐标为_______． 8．已知实数 a ，b 满足 1a b  ， 2 2 0a ab   ，当1 2x  时， 函数 ( 0)ay ax   的最大值与最小值之差是 1，求 a 的值。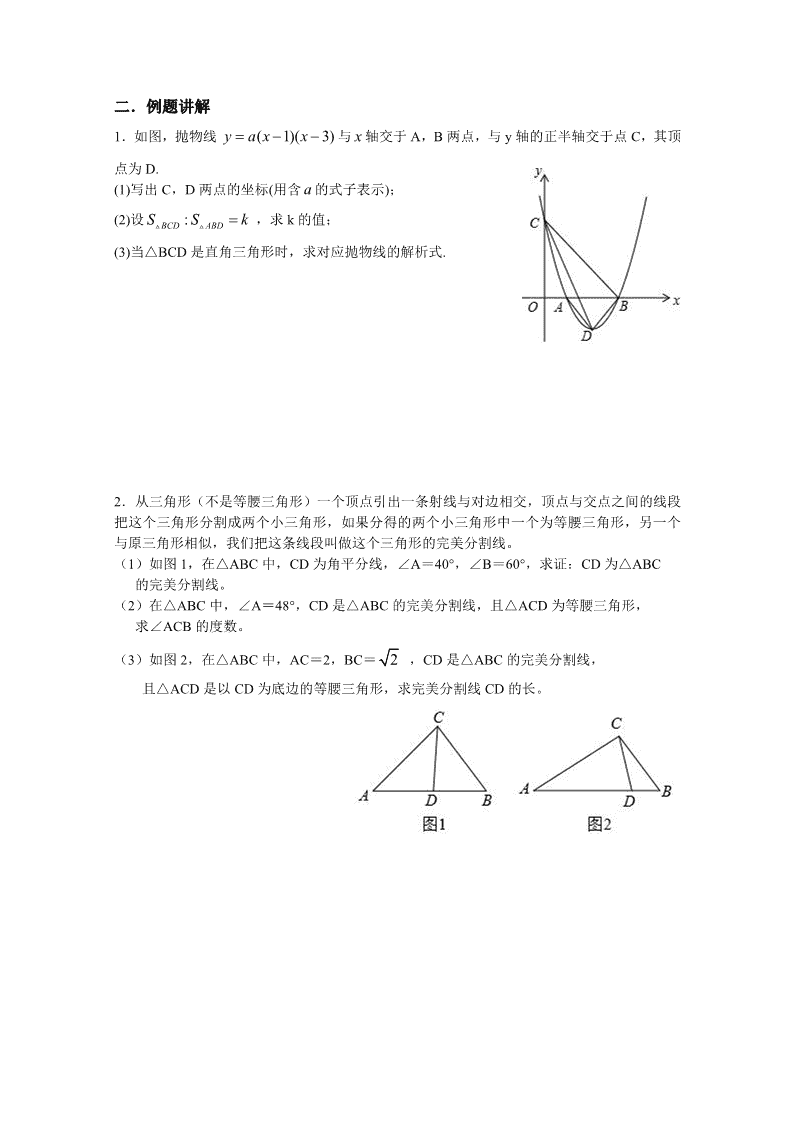 二．例题讲解 1．如图，抛物线 ( 1)( 3)y a x x   与 x 轴交于 A，B 两点，与 y 轴的正半轴交于点 C，其顶 点为 D. (1)写出 C，D 两点的坐标(用含 a 的式子表示)； (2)设 :BCD ABDS S k  ，求 k 的值； (3)当△BCD 是直角三角形时，求对应抛物线的解析式. 2．从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段 把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个 与原三角形相似，我们把这条线段叫做这个三角形的完美分割线。 （1）如图 1，在△ABC 中，CD 为角平分线，∠A＝40°，∠B＝60°，求证：CD 为△ABC 的完美分割线。 （2）在△ABC 中，∠A＝48°，CD 是△ABC 的完美分割线，且△ACD 为等腰三角形， 求∠ACB 的度数。 （3）如图 2，在△ABC 中，AC＝2，BC＝ 2 ，CD 是△ABC 的完美分割线， 且△ACD 是以 CD 为底边的等腰三角形，求完美分割线 CD 的长。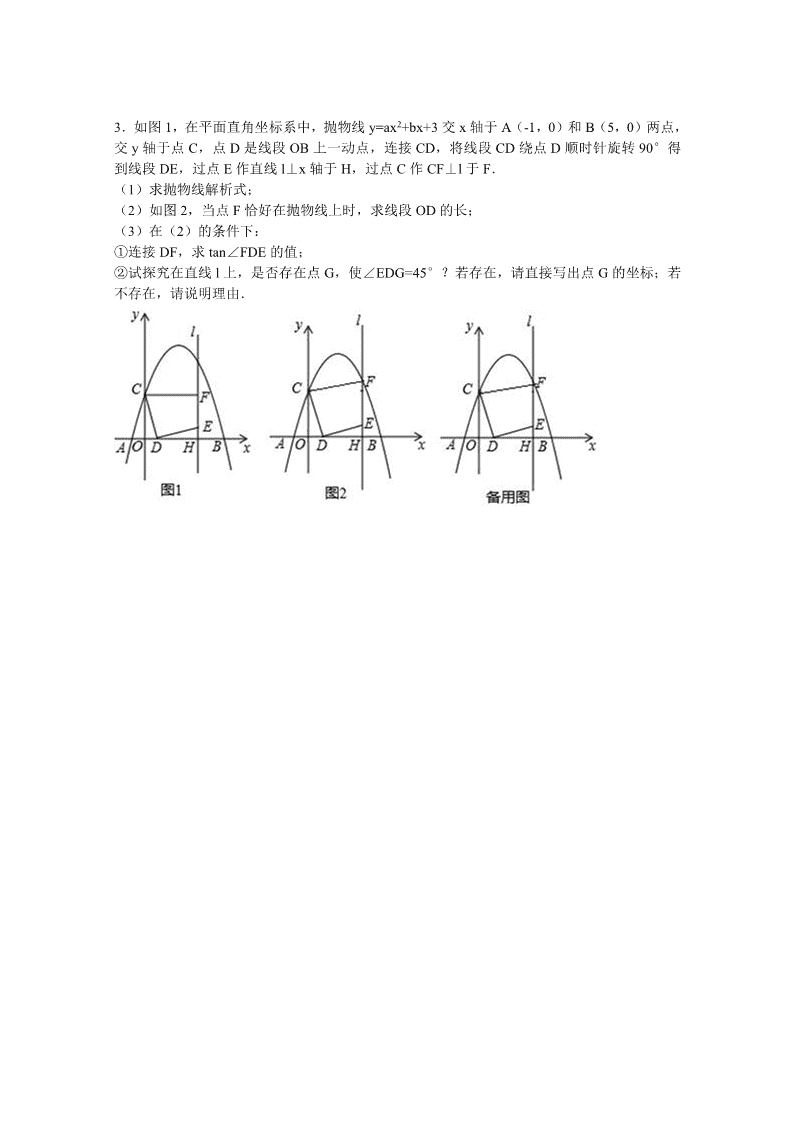 3．如图 1，在平面直角坐标系中，抛物线 y=ax2+bx+3 交 x 轴于 A（-1，0）和 B（5，0）两点， 交 y 轴于点 C，点 D 是线段 OB 上一动点，连接 CD，将线段 CD 绕点 D 顺时针旋转 90°得 到线段 DE，过点 E 作直线 l⊥x 轴于 H，过点 C 作 CF⊥l 于 F． （1）求抛物线解析式； （2）如图 2，当点 F 恰好在抛物线上时，求线段 OD 的长； （3）在（2）的条件下： ①连接 DF，求 tan∠FDE 的值； ②试探究在直线 l 上，是否存在点 G，使∠EDG=45°？若存在，请直接写出点 G 的坐标；若 不存在，请说明理由． 4．如图，在平面直角坐标系中，抛物线 y=ax2+bx-2 与 x 轴交于点 A（-1，0）、B（4，0）．点 M、N 在 x 轴上，点 N 在点 M 右侧，MN=2．以 MN 为直角边向上作等腰直角三角形 CMN， ∠CMN=90°．设点 M 的横坐标为 m． （1）求这条抛物线所对应的函数关系式． （2）求点 C 在这条抛物线上时 m 的值． （3）将线段 CN 绕点 N 逆时针旋转 90°后，得到对应线段 DN． ①当点 D 在这条抛物线的对称轴上时，求点 D 的坐标． ②以 DN 为直角边作等腰直角三角形 DNE，当点 E 在这条抛物线的对称轴上时，直接写出所 有符合条件的 m 值．