全国100套中考数学压轴题分类解析汇编专题1函数问题 54页

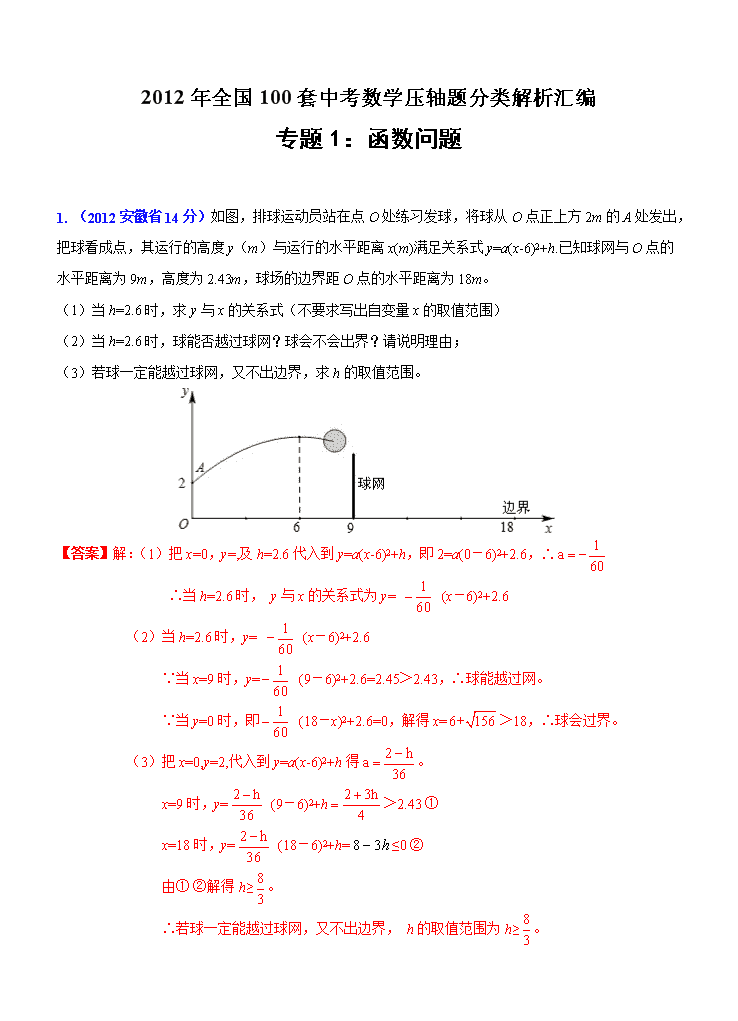
‎2012年全国100套中考数学压轴题分类解析汇编 专题1：函数问题 ‎1. （2012安徽省14分）如图，排球运动员站在点O处练习发球，将球从O点正上方‎2m的A处发出，把球看成点，其运行的高度y（m）与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为‎9m，高度为‎2.43m，球场的边界距O点的水平距离为‎18m。‎ ‎（1）当h=2.6时，求y与x的关系式（不要求写出自变量x的取值范围）‎ ‎（2）当h=2.6时，球能否越过球网？球会不会出界？请说明理由；‎ ‎（3）若球一定能越过球网，又不出边界，求h的取值范围。‎ ‎【答案】解：（1）把x=0，y=,及h=2.6代入到y=a(x-6)2+h，即2=a(0－6)2+2.6，∴ ‎ ‎ ∴当h=2.6时， y与x的关系式为y= (x－6)2+2.6‎ ‎（2）当h=2.6时，y= (x－6)2+2.6‎ ‎∵当x=9时，y= (9－6)2+2.6=2.45＞2.43，∴球能越过网。‎ ‎∵当y=0时，即 (18－x)2+2.6=0，解得x=＞18，∴球会过界。‎ ‎（3）把x=0,y=2,代入到y=a(x-6)2+h得。‎ x=9时，y= (9－6)2+h＞2.43 ①‎ x=18时，y= (18－6)2+h=≤0 ②‎ 由① ②解得h≥。‎ ‎∴若球一定能越过球网，又不出边界， h的取值范围为h≥。‎ ‎【考点】二次函数的性质和应用。‎ ‎【分析】（1）利用h=2.6，将（0，2）点，代入解析式求出即可。‎ ‎（2）利用h=2.6，当x=9时，y= (9－6)2+2.6=2.45与球网高度比较；当y=0时，解出x值与球场的边界距离比较，即可得出结论。‎ ‎（3）根据球经过点（0，2）点，得到a与h的关系式。由x=9时球一定能越过球网得到y＞2.43；由x=18时球不出边界得到y≤0。分别得出h的取值范围，即可得出答案。‎ ‎2. （2012宁夏区10分）某超市销售一种新鲜“酸奶”， 此“酸奶”以每瓶3元购进，5元售出.这种“酸奶”的保质期不超过一天，对当天未售出的“酸奶”必须全部做销毁处理.‎ ‎（1）该超市某一天购进20瓶酸奶进行销售.若设售出酸奶的瓶数为x（瓶），销售酸奶的利润为y（元），写出这一天销售酸奶的利润y（元）与售出的瓶数x（瓶）之间的函数关系式。为确保超市在销售这20瓶酸奶时不亏本，当天至少应售出多少瓶？‎ ‎（2）小明在社会调查活动中，了解到近10天当中，该超市每天购进酸奶20瓶的销售情况统计如下：‎ 每天售出瓶数 ‎17‎ ‎18‎ ‎19‎ ‎20‎ 频数 ‎1‎ ‎2‎ ‎2‎ ‎5‎ 根据上表，求该超市这10天每天销售酸奶的利润的平均数；‎ ‎（3）小明根据（2）中，10天酸奶的销售情况统计，计算得出在近10天当中，其实每天购进19瓶总获利要比每天购进20瓶总获利还多.你认为小明的说法有道理吗？试通过计算说明.‎ ‎【答案】解：（1）由题意知，这一天销售酸奶的利润y（元）与售出的瓶数x（瓶）之间的函数关系式 为y=5x－60 ‎ 当5x－60≥0时，x≥12，‎ ‎∴当天至少应售出12瓶酸奶超市才不亏本。‎ ‎（2）在这10天当中，利润为25元的有1天，30元的有2天，35元的有2天，40元的有 ‎5天，‎ ‎∴这10天中，每天销售酸奶的利润的平均数为（25+30×2+35×2+40×5）÷10=35.5 。‎ ‎（3）小明说的有道理。理由如下：‎ ‎∵在这10天当中，每天购进20瓶获利共计355元.‎ 而每天购进19瓶销售酸奶的利润y（元）与售出的瓶数x（瓶）之间的函数关系式为：y=5x－57‎ ‎ 在10天当中，利润为28元的有1天，33元的有2天，38元的有7天，‎ 总获利为28+33×2+38×7=360>355 。‎ ‎∴小明说的有道理。‎ ‎【考点】一次函数的应用。‎ ‎【分析】（1）根据此“酸奶”以每瓶3元购进，5元售出，该超市某一天购进20瓶酸奶进行销售，即可得出y与x的函数关系式，再利用y大于0得出x的取值范围。‎ ‎（2）根据频数分布表得出总数，从而得出平均数即可。‎ ‎（3）利用每天购进19瓶销售酸奶的利润y（元）与售出的瓶数x（瓶）之间的函数关系式，得出在10天当中，利润为28元的有1天，33元的有2天，8元的有7天，从而得出总利润，比较即可得出答案。‎ ‎3. （2012上海市12分）如图，在平面直角坐标系中，二次函数y=ax2+6x+c的图象经过点A（4，0）、B（﹣1，0），与y轴交于点C，点D在线段OC上，OD=t，点E在第二象限，∠ADE=90°，tan∠DAE=，EF⊥OD，垂足为F．‎ ‎（1）求这个二次函数的解析式；‎ ‎（2）求线段EF、OF的长（用含t的代数式表示）；‎ ‎（3）当∠ECA=∠OAC时，求t的值．‎ ‎【答案】解：（1）二次函数y=ax2+6x+c的图象经过点A（4，0）、B（﹣1，0），‎ ‎∴，解得。‎ ‎∴这个二次函数的解析式为：y=﹣2x2+6x+8。‎ ‎（2）∵∠EFD=∠EDA=90°，∴∠DEF+∠EDF=90°，∠EDF+∠ODA=90°。‎ ‎∴∠DEF=∠ODA。‎ ‎∴△EDF∽△DAO。∴。‎ ‎∵，∴。‎ ‎∵OD=t，∴，∴EF=。‎ 同理，∴DF=2，∴OF=t﹣2。‎ ‎（3）∵抛物线的解析式为：y=﹣2x2+6x+8，∴C（0，8），OC=8。‎ 如图，连接EC、AC，过A作EC的垂线交CE于G点．‎ ‎∵∠ECA=∠OAC，∴∠OAC=∠GCA（等角的余角相等）。‎ 在△CAG与△OCA中，‎ ‎∵∠OAC=∠GCA，AC=CA，∠ECA=∠OAC，‎ ‎∴△CAG≌△OCA（ASA）。∴CG=AO=4，AG=OC=8。‎ 如图，过E点作EM⊥x轴于点M，‎ 则在Rt△AEM中，EM=OF=t﹣2，AM=OA+AM=OA+EF=4+，‎ 由勾股定理得： 。‎ 在Rt△AEG中，由勾股定理得：‎ ‎。‎ 在Rt△ECF中，EF=，CF=OC﹣OF=10﹣t，CE=CG+EG=4+‎ 由勾股定理得：EF2+CF2=CE2，即。‎ 解得t1=10（不合题意，舍去），t2=6。‎ ‎∴t=6。‎ ‎【考点】二次函数综合题，曲线上点的坐标与方程的关系，相似三角形的判定和性质，锐角三角函数定义，全等三角形的判定和性质，勾股定理。‎ ‎【分析】（1）已知点A、B坐标，用待定系数法求抛物线解析式即可。‎ ‎ （2）先证明△EDF∽△DAO，然后利用相似三角形对应边的比例关系以及三角形函数的定义求 解。‎ ‎（3）通过作辅助线构造一对全等三角形：△CAG≌△OCA，得到CG、AG的长度；然后利用勾股定理求得AE、EG的长度（用含t的代数式表示）；最后在Rt△ECF中，利用勾股定理，得到关于t的无理方程，解方程求出t的值。‎ ‎4. （2012天津市10分）已知抛物线y=ax2+bx+c（0＜‎2a＜b）的顶点为P（x0，y0），点A（1，yA）、B（0，yB）、C（－1，yC）在该抛物线上．‎ ‎（Ⅰ）当a=1，b=4，c=10时，①求顶点P的坐标；②求-的值；‎ ‎（Ⅱ）当y0≥0恒成立时，求的最小值．‎ ‎【答案】解：（Ⅰ）若a=1，b=4，c=10，此时抛物线的解析式为y=x2+4x+10。‎ ‎ ①∵y=x2+4x+10=（x+2）2+6，∴抛物线的顶点坐标为P（－2，6）。‎ ‎②∵点A（1，yA）、B（0，yB）、C（－1，yC）在抛物线y=x2+4x+10上，‎ ‎∴yA=15，yB=10，yC=7。∴。‎ ‎（Ⅱ）由0＜‎2a＜b，得。‎ 由题意，如图过点A作AA1⊥x轴于点A1，‎ 则AA1=yA，OA1=1。‎ 连接BC，过点C作CD⊥y轴于点D，‎ 则BD=yB－yC，CD=1。‎ 过点A作AF∥BC，交抛物线于点E（x1，yE），交x轴于点F（x2，0）。‎ 则∠FAA1=∠CBD。∴Rt△AFA1∽Rt△BCD。‎ ‎∴ ，即。‎ 过点E作EG⊥AA1于点G，易得△AEG∽△BCD。‎ ‎∴，即。‎ ‎∵点A（1，yA）、B（0，yB）、C（－1，yC）、E（x1，yE）在抛物线y=ax2+bx+c上，‎ ‎∴yA=a+b+c，yB=c，yC=a－b+c，yE=ax12+bx1+c，‎ ‎∴，化简，得x12＋x1－2=0，‎ 解得x1=－2（x1=1舍去）。‎ ‎∵y0≥0恒成立，根据题意，有x2≤x1＜－1。‎ 则1－x2≥1－x1，即1－x2≥3。‎ ‎∴的最小值为3。 ‎ ‎【考点】二次函数综合题，二次函数的性质，曲线上点的坐标与方程的关系，相似三角形的判定和性质。‎ ‎【分析】（Ⅰ）将a=1，b=4，c=10代入解析式，即可得到二次函数解析式。‎ ‎①将二次函数化为顶点式，即可得到得到抛物线顶点坐标。‎ ‎②将A（1，yA）、B（0，yB）、C（－1，yC）分别代入解析式，即可求出yA、yB、yC的值，然后计算的值即可。‎ ‎（Ⅱ）根据0＜‎2a＜b，求出，作出图中辅助线：点A作AA1⊥x轴于点A1，则AA1=yA，OA1=1．连接BC，过点C作CD⊥y轴于点D，则BD=yB－yC，CD=1．过点A作AF∥BC，交抛物线于点E（x1，yE），交x轴于点F（x2，0）。证出Rt△AFA1∽Rt△BCD，得到，，再根据△AEG∽△BCD得到，然后求出yA、yB、yC、yE的表达式，然后y0≥0恒成立，得到x2≤x1＜－1，从而利用不等式求出 的最小值。 ‎ ‎5. （2012重庆市10分）企业的污水处理有两种方式，一种是输送到污水厂进行集中处理，另一种是通过企业的自身设备进行处理．某企业去年每月的污水量均为12000‎ 吨，由于污水厂处于调试阶段，污水处理能力有限，该企业投资自建设备处理污水，两种处理方式同时进行．1至6月，该企业向污水厂输送的污水量y1（吨）与月份x（1≤x≤6，且x取整数）之间满足的函数关系如下表：‎ ‎7至12月，该企业自身处理的污水量y2（吨）与月份x（7≤x≤12，且x取整数）之间满足二次函数关系式为y2=ax2+c(a≠0)．其图象如图所示．1至6月，污水厂处理每吨污水的费用：z1（元）与月份x之间满足函数关系式：，该企业自身处理每吨污水的费用：z2（元）与月份x之间满足函数关系式：；7至12月，污水厂处理每吨污水的费用均为2元，该企业自身处理每吨污水的费用均为1.5元．‎ ‎（1）请观察题中的表格和图象，用所学过的一次函数、反比例函数或二次函数的有关知识，分别直接写出y1，y2与x之间的函数关系式；‎ ‎（2）请你求出该企业去年哪个月用于污水处理的费用W（元）最多，并求出这个最多费用；‎ ‎（3）今年以来，由于自建污水处理设备的全面运行，该企业决定扩大产能并将所有污水全部自身处理，估计扩大产能后今年每月的污水量都将在去年每月的基础上增加a%，同时每吨污水处理的费用将在去年12月份的基础上增加（a﹣30）%，为鼓励节能降耗，减轻企业负担，财政对企业处理污水的费用进行50%的补助．若该企业每月的污水处理费用为18000元，请计算出a的整数值．‎ ‎（参考数据：≈15.2，≈20.5，≈28.4）‎ ‎【答案】解：（1）根据表格中数据可以得出xy=定值，‎ 则y1与x之间的函数关系为反比例函数关系：。‎ 将（1，12000）代入得：k=1×12000=12000，‎ ‎∴（1≤x≤6，且x取整数）。‎ 根据图象可以得出：图象过（7，10049），（12，10144）点，代入y2=ax2+c得：‎ ‎，解得：。‎ ‎∴y2=x2+10000（7≤x≤12，且x取整数）。‎ ‎（2）当1≤x≤6，且x取整数时：‎ ‎ ‎ ‎=﹣1000x2+10000x﹣3000=﹣1000（x﹣5）2+2200。‎ ‎∵a=﹣1000＜0， 1≤x≤6，∴当x=5时，W最大=22000（元）。‎ 当7≤x≤12时，且x取整数时：‎ W=2×（12000﹣y1）+1.5y2=2×（12000﹣x2﹣10000）+1.5（x2+10000）=﹣x2+1900。‎ ‎∵a=﹣＜0，对称轴为x=0，当7≤x≤12时，W随x的增大而减小，‎ ‎∴当x=7时，W最大=18975.5（元）。‎ ‎∵22000＞18975.5，‎ ‎∴去年5月用于污水处理的费用最多，最多费用是22000元。‎ ‎（3）由题意得：12000（1+a%）×1.5×[1+（a﹣30）%]×（1﹣50%）=18000，‎ 设t=a%，整理得：10t2+17t﹣13=0，解得：。‎ ‎∵≈28.4，∴t1≈0.57，t2≈﹣2.27（舍去）。‎ ‎∴a≈57。‎ 答：a整数值是57。‎ ‎【考点】二次函数的应用，待定系数法，曲线上点的坐标与方程的关系，二次函数的性质，解一元二次方程。‎ ‎【分析】（1）利用表格中数据可以得出xy=定值，则y1与x之间的函数关系为反比例函数关系，求出即可。再利用函数图象得出：图象过（7，10049），（12，10144）点，求出二次函数解析式即可。‎ ‎（2）利用当1≤x≤6时，以及当7≤x≤12时，分别求出处理污水的费用，即可得出答案。‎ ‎（3）利用今年每月的污水量都将在去年每月的基础上增加a%，同时每吨污水处理的费用将在去年12月份的基础上增加（a一30）%，得出等式12000（1+a%）×1.5×[1+（a-30）%]×（1-50%）=18000，进而求出即可。‎ ‎6. （2012福建莆田14分） 如图，在平面直角坐标系中，矩形OABC四个顶点的坐标分别为O(0，0)，A(0，3)，B(6，3)，C(6，0)，抛物线过点A。‎ ‎(1)(2分)求c的值； ．‎ ‎(2)(6分)若a＝－l，且抛物线与矩形有且只有三个交点A、D、E，求△ADE的面积S的最大值；‎ ‎(3)(6分)若抛物线与矩形有且只有三个交点A、M、N，线段MN的垂直平分线l过点O，交线段BC于点 F。当BF＝1时，求抛物线的解析式．‎ ‎【答案】解：(1)∵抛物线过点A(0，3)，∴c＝3。‎ ‎(2) ∵a＝－l，∴‎ ‎ 如图①，当抛物线与矩形的两个交点D、E分别在AB、OC边上时， 抛物线与直线x＝6的交点应落在C点或C点下方。‎ ‎ ∴　当x＝6时，y≤0。‎ ‎∴，即。‎ ‎ 又∵对称轴在y轴右侧，∴b＞0。∴0＜。‎ ‎ 由抛物线的对称性可知： 。‎ ‎ 又∵△ADE的高＝BC＝3，∴S＝×b×3＝。‎ ‎∵＞0，∴S随b的增大而增大。‎ ‎∴当b＝时，S的最大值＝。‎ ‎ 如图②，当抛物线与矩形的两个交点D、E分别在AB、BC边上时，抛物线与直线 x＝6的交点应落在线段BC上且不与点B重合，即0≤＜3。‎ 当x＝6，则，‎ ‎∴0≤6b—33＜3，∴≤b＜6。‎ ‎∴BE＝3－(6b－33)＝36—6b。‎ ‎∴S＝AD·BE＝·b·(36—6b)＝－3b2+18b。‎ ‎∵对称轴b＝3＜，∴随b的增大而减小。‎ ‎∴当b＝时，S的最大值＝。‎ 综上所述：S的最大值为。‎ ‎ (3)当a＞0时，符合题意要求的抛物线不存在。‎ ‎ 当a＜0时，符合题意要求的抛物线有两种情况：‎ ‎①当点M、N分别在AB、OC边上时．‎ 如图③过M点作MG⊥OC于点G，连接OM．‎ ‎ ∴MG＝OA＝3．∠2＋∠MNO＝90°。‎ ‎ ∵OF垂直平分MN．‎ ‎∴OM＝ON，∠1＋∠MNO=90°，∠1＝∠2。‎ ‎ ∵FB＝1，FC＝3－1＝2。‎ ‎ ∴tan∠1＝，tan∠2＝＝tan∠1＝。‎ ‎∴GN＝GM＝1。‎ 设N(n，0)，则G(n－1，0)，∴M(n－1，3)。 ∴AM＝n－1，ON＝n＝OM。 ‎ 在Rt△AOM中，，‎ ‎ ∴，解得n＝5。∴　M(4，3)，N(5，0)。‎ 把M(4，3)，N(5，0)分别代入，得 ‎，解得。‎ ‎∴抛物线的解析式为。‎ ‎②当点M、N分别在AB、BC边上时．如图④，连接MF．‎ ‎ ∵OF垂直平分MN，‎ ‎∴∠1＋∠NFO＝90°，MF＝FN。‎ ‎ 又∵∠0CB＝90°，∴∠2＋∠CFO=90°。‎ ‎ ∴∠1＝∠2。‎ ‎ ∵BF＝1， ∴FC＝2。‎ ‎∴tan∠1＝tan∠2＝。‎ ‎ 在Rt△MBN，tan∠1＝，∴BN＝3MB。‎ 设N(6，n)．则FN＝2－n，BN＝3一n。∴MF＝2－n，MB＝。‎ 在Rt△MBF中，∵，∴。‎ 解得： (不合题意舍去)，∴。‎ ‎∴AM＝6－＝，∴　M(，3)，N(6，) 。‎ 把M(，3)，N(6，)分别代人，得 ‎，解得　。‎ ‎∴抛物线的解析式为。‎ 综上所述，抛物线的解析式为或。‎ ‎【考点】二次函数综合题，曲线上点的坐标与方程的关系，二次函数的性质，矩形的性质，锐角三角函数定义，勾股定理，解二元一次方程组。‎ ‎【分析】（1）将点A的坐标代入即可求得c的值。‎ ‎ （2）分抛物线与矩形的两个交点D、E分别在AB、OC边上和抛物线与矩形的两个交点D、E分别在AB、BC边两种情况应用二次函数性质分别求解。‎ ‎ （3）分抛物线与矩形的两个交点D、E分别在AB、OC边上和抛物线与矩形的两个交点D、E分别在AB、BC边两种情况应用待定系数法分别求解。‎ ‎7. （2012福建厦门12分）已知点A(1，c)和点B (3，d )是直线y＝k1x＋b与双曲线y＝（k2＞0）的交 点．‎ ‎（1）过点A作AM⊥x轴，垂足为M，连结BM．若AM＝BM，求点B的坐标；‎ ‎（2）设点P在线段AB上，过点P作PE⊥x轴，垂足为E，并交双曲线y＝（k2＞0）于点N．当 取最大值时，若PN＝ ，求此时双曲线的解析式．‎ ‎【答案】（1）解：∵点A(1，c)和点B (3，d )在双曲线y＝（k2＞0）上，‎ ‎∴ c＝k2＝3d 。‎ ‎∵ k2＞0， ∴ c＞0，d＞0。 ‎ ‎∴A(1，c)和点B (3，d )都在第一象限。‎ ‎∴ AM＝3d。‎ 过点B作BT⊥AM，垂足为T。‎ ‎∴ BT＝2，TM＝d。‎ ‎∵ AM＝BM，∴ BM＝3d。‎ 在Rt△BTM中，TM 2＋BT2＝BM2，即 d2＋4＝9d2，∴ d＝。‎ ‎∴点B(3，)。‎ ‎（2）∵ 点A(1，c)、B(3，d)是直线y＝k1x＋b与双曲线y＝（k2＞0）的交点，‎ ‎∴c＝k2,，3d＝k2，c＝k1＋b，d＝3k1＋b。‎ ‎∴k1＝－k2，b＝k2。‎ ‎∵ A(1，c)和点B (3，d )都在第一象限，‎ ‎∴ 点P在第一象限。设P（x，k1x＋b），‎ ‎∴＝ ＝x2＋x＝－x2＋x。‎ ‎＝‎ ‎∵当x＝1，3时，＝1，又∵当x＝2时， 的最大值是。‎ ‎∴1≤≤.。∴ PE≥NE。‎ ‎∴ ＝－1＝。‎ ‎∴当x＝2时，的最大值是。‎ 由题意，此时PN＝，∴ NE＝。∴ 点N(2，) 。 ∴ k2＝3。‎ ‎∴此时双曲线的解析式为y＝。‎ ‎【考点】反比例函数综合题，曲线上点的坐标与方程的关系，勾股定理，二次函数的最值。‎ ‎【分析】（1）过点B作BT⊥AM，由点A（1，c）和点B（3，d）都在双曲线y＝（k2＞0）上，得到c=3d，则A点坐标为（1，3d），在Rt△BTM中应用勾股定理即可计算出d的值，即可确定B点坐标。‎ ‎（2）P（x，k1x＋b），求出关于x的二次函数，应用二次函数的最值即可求得的最大值，此时根据PN＝求得NE＝，从而得到N(2，)，代入y＝即可求得k2＝3。因此求得反比例函数的解析式为y＝。‎ ‎8. （2012甘肃兰州10分）若x1、x2是关于一元二次方程ax2＋bx＋c(a≠0)的两个根，则方程的两个根x1、x2和系数a、b、c有如下关系：x1＋x2＝，x1•x2＝．把它称为一元二次方程根与系数关系定理．如果设二次函数y＝ax2＋bx＋c(a≠0)的图象与x轴的两个交点为A(x1，0)，B(x2，0)．利用根与系数关系定理可以得到A、B连个交点间的距离为：AB＝|x1－x2|＝‎ ‎。‎ 参考以上定理和结论，解答下列问题：‎ 设二次函数y＝ax2＋bx＋c(a＞0)的图象与x轴的两个交点A(x1，0)，B(x2，0)，抛物线的顶点为C ‎，显然△ABC为等腰三角形．‎ ‎(1)当△ABC为直角三角形时，求b2－‎4ac的值；‎ ‎(2)当△ABC为等边三角形时，求b2－‎4ac的值．‎ ‎【答案】解：（1）当△ABC为直角三角形时，‎ 过C作CE⊥AB于E，则AB＝2CE。‎ ‎∵抛物线与x轴有两个交点，△＝b2－‎4ac＞0，‎ 则|b2－‎4ac|＝b2－‎4ac。‎ ‎∵a＞0，∴AB。‎ 又∵CE，∴。‎ ‎∴，即。‎ ‎∵b2－‎4ac＞0，∴b2－‎4ac＝4。‎ ‎（2）当△ABC为等边三角形时，由(1)可知CE＝AB，‎ ‎∴。‎ ‎∵b2－‎4ac＞0，∴b2－‎4ac＝12。‎ ‎【考点】抛物线与x轴的交点，根与系数的关系，等腰三角形的性质，等边三角形的性质。‎ ‎【分析】（1）当△ABC为直角三角形时，由于AC＝BC，所以△ABC为等腰直角三角形，过C作CE⊥AB于E，则AB＝2CE．根据本题定理和结论，得到AB，根据顶点坐标公式，得到CE ‎，列出方程，解方程即可求出b2－‎4ac的值。‎ ‎（2）当△ABC为等边三角形时，解直角△ACE，得CE＝AB，据此列出方程，解方程即可求出b2－‎4ac的值。‎ ‎9. 2012广东深圳9分）如图，已知△ABC的三个顶点坐标分别为A(－4，0)、B(1，0)、C(－2，6)．‎ ‎(1)求经过A、B、C三点的抛物线解析式；‎ ‎(2)设直线BC交y轴于点E，连接AE，求证：AE=CE;[来源:Z&xx&k.Com]‎ ‎(3)设抛物线与y轴交于点D，连接AD交BC于点F，试问以A、B、F，为顶点的三角形与△ABC相似吗？‎ ‎ 请说明理由．‎ ‎【答案】解：（1）∵抛物线经过A(－4，0)、B(1，0)，∴设函数解析式为：y=a（x＋4）（x－1）。‎ 又∵由抛物线经过C（－2，6），∴6=a（－2＋4）（－2－1），解得： a=－1。‎ ‎ ∴经过A、B、C三点的抛物线解析式为：y=－（x＋4）（x－1），即y=－x2－3x＋4。‎ ‎（2）证明：设直线BC的函数解析式为y=kx+b，‎ 由题意得： ，解得：。‎ ‎∴直线BC的解析式为y=－2x+2．‎ ‎∴点E的坐标为（0，2）。‎ ‎∴。 ‎ ‎∴AE=CE。‎ ‎（3）相似。理由如下：‎ 设直线AD的解析式为y=k1x+b1，则 ，解得：。‎ ‎∴直线AD的解析式为y=x+4。‎ 联立直线AD与直线BC的函数解析式可得：，解得：。‎ ‎∴点F的坐标为（ ）。‎ 则。‎ 又∵AB=5，，‎ ‎∴。∴。‎ 又∵∠ABF=∠CBA，∴△ABF∽△CBA。‎ ‎∴以A、B、F为顶点的三角形与△ABC相似。‎ ‎【考点】二次函数综合题，待定系数法，曲线上点的坐标与方程的关系，勾股定理，相似三角形的判定。‎ ‎【分析】（1）利用待定系数法求解即可得出抛物线的解析式。‎ ‎（2）求出直线BC的函数解析式，从而得出点E的坐标，然后分别求出AE及CE的长度即可证明出结论。‎ ‎（3）求出AD的函数解析式，然后结合直线BC的解析式可得出点F的坐标，根据勾股定理分别求出BF，BC 得出；由题意得∠ABF=∠CBA， 即可作出判断。‎ ‎10. （2012广东肇庆10分）已知二次函数图象的顶点横坐标是2，与x轴交于A（x1，0）、‎ B（x2，0），x1﹤0﹤x2，与y轴交于点C，O为坐标原点，．‎ ‎（1）求证： ；‎ ‎（2）求m、n的值；‎ ‎（3）当p﹥0且二次函数图象与直线仅有一个交点时，求二次函数的最大值．‎ ‎【答案】（1）证明：∵二次函数图象的顶点横坐标是2，‎ ‎∴抛物线的对称轴为x=2，即，化简得：n+‎4m=0。‎ ‎（2）解：∵二次函数与x轴交于A（x1，0）、B（x2，0），x1＜0＜x2，‎ ‎∴OA=－x1，OB=x2；。‎ 令x=0，得y=p，∴C（0，p），∴OC=|p|。‎ 由三角函数定义得：。‎ ‎∵tan∠CAO－tan∠CBO=1，即 ，化简得：。‎ 将 代入得：，化简得：。‎ 由（1）知n+‎4m=0，‎ ‎∴当n=1时，；当n=－1时，。‎ ‎∴m、n的值为： ，n=－1（此时抛物线开口向上）或 ，n=1（此时抛物线开口向下）。‎ ‎（3）解：由（2）知，当p＞0时，n=1， ，‎ ‎∴抛物线解析式为：。‎ 联立抛物线与直线y=x+3解析式得到：，‎ 化简得： ＊。‎ ‎∵二次函数图象与直线y=x+3仅有一个交点，‎ ‎∴一元二次方程＊根的判别式等于0，即△=02+16（p－3）=0，解得p=3。‎ ‎∴抛物线解析式为：。‎ 当x=2时，二次函数有最大值，最大值为4。‎ ‎∴当p＞0且二次函数图象与直线y=x+3仅有一个交点时，二次函数的最大值为4。‎ ‎【考点】二次函数综合题，曲线上点的坐标与方程的关系，一元二次方程根的判别式和根与系数的关系，锐角三角函数定义，二次函数的性质。‎ ‎【分析】（1）由题意可知抛物线的对称轴为x=2，利用对称轴公式，化简即得n+‎4m=0。‎ ‎（2）利用三角函数定义和抛物线与x 轴交点坐标性质求解．特别需要注意的是抛物线的开口方向未定，所以所求m、n的值将有两组。‎ ‎（3）利用一元二次方程的判别式等于0求解．当p＞0时，m、n的值随之确定；将抛物线的解析式与直线的解析式联立，得到一个一元二次方程；由交点唯一可知，此一元二次方程的判别式等于0，据此求出p的值，从而确定了抛物线的解析式；最后由抛物线的解析式确定其最大值。 ‎ ‎11. （2012贵州六盘水10分）为鼓励居民节约用水，某市决定对居民用水收费实行“阶梯价”，即当每月用水量不超过15吨时（包括15吨），采用基本价收费；当每月用水量超过15吨时，超过部分每吨采用市场价收费．小兰家4、5月份的用水量及收费情况如下表：‎ 月份 用水量（吨）‎ 水费（元）‎ ‎4‎ ‎22‎ ‎51‎ ‎5‎ ‎20‎ ‎45‎ ‎（1）求该市每吨水的基本价和市场价．‎ ‎（2）设每月用水量为n吨，应缴水费为m元，请写出m与n之间的函数关系式．‎ ‎（3）小兰家6月份的用水量为26吨，则她家要缴水费多少元？‎ ‎【答案】解：（1）根据当每月用水量不超过15吨时（包括15吨），采用基本价收费；当每月用水量超过15吨时，超过部分每吨采用市场价收费，‎ ‎∵4月份用水22吨，水费51元，5月份用水20吨，水费45元，‎ ‎∴市场价收费标准为：（51﹣45）÷（22﹣20）=3（元/吨）。‎ 设基本价收费为x元/吨，‎ 根据题意得出：15x+（22﹣15）×3=51，解得：x=2。‎ ‎∴该市每吨水的基本价和市场价分别为：3元/吨，2元/吨。‎ ‎（2）当n≤15时，m=2n，当n＞15时，m=15×2+（n﹣15）×3=3n－15。‎ ‎∴m与n之间的函数关系式为。-‎ ‎（3）∵小兰家6月份的用水量为26吨，‎ ‎∴她家要缴水费3×26－15=63元。‎ ‎【考点】一元一次方程和一次函数的应用。‎ ‎【分析】（1）利用已知得出4月份用水22吨，水费51元，5月份用水20吨，水费45元，求出市场价收费标准为：（51﹣45）÷（22﹣20）=3（元/吨），进而得出每吨水的基本价。‎ ‎（2）利用（1）中所求不同水价，再利用当n≤15时，m=2n，当n＞15时，分别求出即可。‎ ‎（3）根据（2）中所求得出，用水量为26吨时要缴水费。‎ ‎12. （2012贵州黔东南12分）我州某教育行政部门计划今年暑假组织部分教师到外地进行学习，预订宾馆住宿时，有住宿条件一样的甲、乙两家宾馆供选择，其收费标准均为每人每天120元，并且各自推出不同的优惠方案．甲家是35人（含35人）以内的按标准收费，超过35人的，超出部分按九折收费；乙家是45人（含45人）以内的按标准收费，超过45人的，超出部分按八折收费．如果你是这个部门的负责人，你应选哪家宾馆更实惠些？‎ ‎【答案】解：设总人数是x，‎ 当x≤35时，选择两个，宾馆是一样的；当35＜x≤45时，选择甲宾馆比较便宜；‎ 当x＞45时，甲宾馆的收费是：y甲=35×120+0.9×120×（x﹣35）=108x+420；‎ 乙宾馆的收费是y乙=45×120+0.8×120（x﹣45）=96x+1080。‎ 当y甲=y乙时，108x+420=96x+1080，解得：x=55；‎ 当y甲＞y乙时，即108x+420＞96x+1080，解得：x＞55；‎ 当y甲＜y乙时，即108x+420＜96x+1080，解得：x＜55。‎ 综上所述，当x≤35或x=55时，选择两个宾馆是一样的；‎ 当35＜x＜55时，选择甲宾馆比较便宜。‎ 当x＞55时，选乙宾馆比较便宜。‎ ‎【考点】一次函数的应用。‎ ‎【分析】当x≤35时，选择两个，宾馆是一样的；当35＜x≤45时，选择甲宾馆比较便宜，当x＞35时，两个宾馆的收费可以表示成人数x的函数，比较两个函数值的大小即可。‎ ‎13. （2012贵州铜仁12分）为了抓住梵净山文化艺术节的商机，某商店决定购进A、B两种艺术节纪念品．若购进A种纪念品8件，B种纪念品3件，需要950元；若购进A种纪念品5件，B种纪念品6件，需要800元．‎ ‎（1）求购进A、B两种纪念品每件各需多少元？‎ ‎（2）若该商店决定购进这两种纪念品共100件，考虑市场需求和资金周转，用于购买这100件纪念品的资金不少于7500元，但不超过7650元，那么该商店共有几种进货方案？‎ ‎（3）若销售每件A种纪念品可获利润20元，每件B种纪念品可获利润30元，在第（2）问的各种进货方案中，哪一种方案获利最大？最大利润是多少元？‎ ‎【答案】解：（1）设该商店购进一件A种纪念品需要a元，购进一件B种纪念品需要b元，‎ ‎ 根据题意得方程组得：， 解方程组得：。‎ ‎∴购进一件A种纪念品需要100元，购进一件B种纪念品需要50元。‎ ‎（2）设该商店购进A种纪念品x个，则购进B种纪念品有（100﹣x）个，‎ ‎∴，解得：50≤x≤53。‎ ‎∵x 为正整数，∴x=50，51，52，53。∴共有4种进货方案。‎ ‎（3）∵B种纪念品利润较高，∴B种数量越多总利润越高。‎ ‎∴选择购A种50件，B种50件。‎ 总利润=50×20+50×30=2500（元）。‎ ‎∴当购进A种纪念品50件，B种纪念品50件时，可获最大利润，最大利润是2500元。‎ ‎【考点】二元一次方程组和一元一次不等式组的应用。‎ ‎【分析】（1）方程（组）的应用解题关键是找出等量关系，列出方程求解。本题等量关系为：‎ ‎ 购进A种纪念品8件＋B种纪念品3件=950元 购进A种纪念品5件＋B种纪念品6件=800元。‎ ‎（2）不等式的应用解题关键是找出不等量关系，列出不等式求解。本题不等量关系为：‎ 购买这100件纪念品的资金不少于7500元，不超过7650元。‎ ‎ （3）因为B种纪念品利润较高，所以选取B种数量多的方案即可求解。‎ ‎14. （2012湖北黄石10分）已知抛物线C1的函数解析式为，若抛物线C1经过 点，方程的两根为，，且。‎ ‎（1）求抛物线C1的顶点坐标.‎ ‎（2）已知实数，请证明：≥,并说明为何值时才会有.‎ ‎（3）若抛物线先向上平移4个单位，再向左平移1个单位后得到抛物线C2，设， ‎ 是C2上的两个不同点，且满足： ，，.请你用含有的表达式表示出△AOB的面积S，并求出S的最小值及S取最小值时一次函数OA的函数解析式。‎ ‎（参考公式：在平面直角坐标系中，若，，则P，Q两点间的距离）‎ ‎【答案】解：（1）∵抛物线过（０,－３）点，∴－‎3a＝－３。∴a＝１ 。‎ ‎　∴ｙ＝x2＋bx－３‎ ‎　　　　　 ∵x2＋bx－３=０的两根为x1，x2且，‎ ‎∴＝４且b＜０。∴b＝－２。‎ ‎∴。‎ ‎∴抛物线Ｃ１的顶点坐标为（１，－４）。‎ ‎（2）∵x＞０，∴‎ ‎∴。‎ 当时，即当x＝１时，有。 ‎ ‎（3）由平移的性质，得C2的解析式为：y＝x2 。‎ ‎∴Ａ(m，m2)，B（n，n2）。‎ ‎∵ΔAOB为直角三角形，∴OA2＋OB2=AB2。‎ ‎∴m2＋m4＋n2＋n4＝（m－n）2＋（m2－n2）2，‎ 化简得：m n＝－１。‎ ‎∵ＳΔAOB=，m n＝－１，‎ ‎∴ＳΔAOB＝＝。‎ ‎∴ＳΔAOB的最小值为１，此时m＝１,Ａ(１,１)。‎ ‎∴直线OA的一次函数解析式为ｙ＝x。‎ ‎【考点】二次函数综合题，曲线上点的坐标与方程的关系，一元二次方程根与系数的关系，二次函数的性质，不等式的知识。‎ ‎【分析】（1）求抛物线的顶点坐标，即要先求出抛物线的解析式，即确定待定系数a、b的值．已知抛物线图象与y轴交点，可确定解析式中的常数项（由此得到a的值）；然后从方程入手求b的值，题目给出了两根差的绝对值，将其进行适当变形（转化为两根和、两根积的形式），结合根与系数的关系即可求出b的值。‎ ‎（2）将配成完全平方式，然后根据平方的非负性即可得证。‎ ‎（3）结合（1）的抛物线的解析式以及函数的平移规律，可得出抛物线C2的解析式；在Rt△OAB中，由勾股定理可确定m、n的关系式，然后用m列出△AOB的面积表达式，结合不等式的相关知识可确定△OAB的最小面积值以及此时m的值，从而由待定系数法确定一次函数OA的解析式。‎ 别解：由题意可求抛物线C2的解析式为：y＝x2。‎ ‎∴Ａ(m，m2)，B（n，n2）。‎ 过点A、B作x轴的垂线，垂足分别为C、D，‎ 则 由 得 ，即。∴。‎ ‎∴。‎ ‎∴ＳΔAOB的最小值为１，此时m＝１,Ａ(１,１)。‎ ‎∴直线OA的一次函数解析式为ｙ＝x。‎ ‎15. （2012湖北荆门10分）已知：y关于x的函数y=（k﹣1）x2﹣2kx+k+2的图象与x轴有交点．‎ ‎（1）求k的取值范围；‎ ‎（2）若x1，x2是函数图象与x轴两个交点的横坐标，且满足（k﹣1）x12+2kx2+k+2=4x1x2．‎ ‎①求k的值；②当k≤x≤k+2时，请结合函数图象确定y的最大值和最大值．‎ ‎【答案】解：（1）当k=1时，函数为一次函数y=﹣2x+3，其图象与x轴有一个交点。‎ 当k≠1时，函数为二次函数，其图象与x轴有一个或两个交点，‎ 令y=0得（k﹣1）x2﹣2kx+k+2=0．‎ ‎△=（﹣2k）2﹣4（k﹣1）（k+2）≥0，解得k≤2．即k≤2且k≠1。‎ 综上所述，k的取值范围是k≤2。‎ ‎（2）①∵x1≠x2，由（1）知k＜2且k≠1。‎ 由题意得（k﹣1）x12+（k+2）=2kx1（*），‎ 将（*）代入（k﹣1）x12+2kx2+k+2=4x1x2中得：2k（x1+x2）=4x1x2。‎ 又∵x1+x2=，x1x2=，∴2k•=4•，‎ 解得：k1=﹣1，k2=2（不合题意，舍去）。∴所求k值为﹣1。‎ ‎②如图，∵k1=﹣1，y=﹣2x2+2x+1=﹣2（x﹣）2+，且﹣1≤x≤1，‎ 由图象知：当x=﹣1时，y最小=﹣3；当x=时，y最大=。‎ ‎∴y的最大值为，最小值为﹣3。‎ ‎【考点】抛物线与x轴的交点，一次函数的定义，一元二次方程根的判别式和根与系数物关系，二次函数的最值。‎ ‎【分析】（1）分两种情况讨论，当k=1时，可求出函数为一次函数，必与x轴有一交点；当k≠1时，函数为二次函数，若与x轴有交点，则△≥0。‎ ‎（2）①根据（k﹣1）x12+2kx2+k+2=4x1x2及根与系数的关系，建立关于k的方程，求出k的值。②充分利用图象，直接得出y的最大值和最小值。‎ ‎16. （2012湖南长沙10分）在长株潭建设两型社会的过程中，为推进节能减排，发展低碳经济，我市某公司以25万元购得某项节能产品的生产技术后，再投入100万元购买生产设备，进行该产品的生产加工．已知生产这种产品的成本价为每件20元．经过市场调研发现，该产品的销售单价定在25元到30元之间较为合理，并且该产品的年销售量y（万件）与销售单价x（元）之间的函数关系式为：.‎ ‎（年获利=年销售收入﹣生产成本﹣投资成本）‎ ‎（1）当销售单价定为28元时，该产品的年销售量为多少万件？‎ ‎（2）求该公司第一年的年获利W（万元）与销售单价x（元）之间的函数关系式，并说明投资的第一年，该公司是盈利还是亏损？若盈利，最大利润是多少？若亏损，最小亏损是多少？‎ ‎（3）第二年，该公司决定给希望工程捐款Z万元，该项捐款由两部分组成：一部分为10万元的固定捐款；另一部分则为每销售一件产品，就抽出一元钱作为捐款．若除去第一年的最大获利（或最小亏损）以及第二年的捐款后，到第二年年底，两年的总盈利不低于67.5万元，请你确定此时销售单价的范围．‎ ‎【答案】解：（1）∵25≤28≤30，，‎ ‎∴把28代入y=40﹣x得， y=12（万件）。‎ 答：当销售单价定为28元时，该产品的年销售量为12万件。‎ ‎（2）①当 25≤x≤30时，‎ W=（40﹣x）（x﹣20）﹣25﹣100=﹣x2+60x﹣925=﹣（x﹣30）2﹣25，‎ ‎∴当x=30时，W最大为﹣25，即公司最少亏损25万。‎ ‎②当30＜x≤35时，‎ W=（25﹣0.5x）（x﹣20）﹣25﹣100=﹣x2+35x﹣625=﹣（x﹣35）2﹣12.5，‎ ‎∴当x=35时，W最大为﹣12.5，即公司最少亏损12.5万。‎ 综合①，②得，投资的第一年，公司亏损，最少亏损是12.5万。‎ 答：投资的第一年，公司亏损，最少亏损是12.5万。‎ ‎（3）①当 25≤x≤30时，W=（40﹣x）（x﹣20﹣1）﹣12.5﹣10=﹣x2+59x﹣782.5，‎ 令W=67.5，则﹣x2+59x﹣782.5=67.5，化简得：x2﹣59x+850=0，‎ 解得 x1=25；x2=34。‎ 此时，当两年的总盈利不低于67.5万元，25≤x≤30；‎ ‎②当30＜x≤35时，W=（25﹣0.5x）（x﹣20﹣1）﹣12.5﹣10=﹣x2+35.5x﹣547.5，‎ 令W=67.5，则﹣x2+35.5x﹣547.5=67.5，化简得：x2﹣71x+1230=0，‎ 解得x1=30；x2=41。‎ 此时，当两年的总盈利不低于67.5万元，30＜x≤35，‎ 综上所述，到第二年年底，两年的总盈利不低于67.5万元，此时销售单价的范围是25≤x≤35。‎ ‎【考点】一、二次函数的应用。‎ ‎【分析】（1）因为25≤28≤30，所以把28代入y=40－x即可求出该产品的年销售量为多少万件。‎ ‎（2）由（1）中y于x的函数关系式和根据年获利=年销售收入－生产成本－投资成本，得到w和x的二次函数关系，再由x的取值范围不同分别讨论即可知道该公司是盈利还是亏损。 ‎ ‎（3）由条件得到w和x在自变量x的不同取值范围的函数关系式，再分别令w=67.5，求出对应x的值，结合y于x的关系中的x取值范围即可确定此时销售单价的范围。‎ ‎17. （2012湖南岳阳10分）我们常见的炒菜锅和锅盖都是抛物线面，经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形，不妨简称为“锅线”，锅口直径为6dm，锅深3dm，锅盖高1dm（锅口直径与锅盖直径视为相同），建立直接坐标系如图①所示，如果把锅纵断面的抛物线的记为C1，把锅盖纵断面的抛物线记为C2．‎ ‎（1）求C1和C2的解析式；‎ ‎（2）如图②，过点B作直线BE：y=x﹣1交C1于点E（﹣2，﹣），连接OE、BC，在x轴上求一点P，使以点P、B、C为顶点的△PBC与△BOE相似，求出P点的坐标；‎ ‎（3）如果（2）中的直线BE保持不变，抛物线C1或C2上是否存在一点Q，使得△EBQ的面积最大？若存在，求出Q的坐标和△EBQ面积的最大值；若不存在，请说明理由．‎ ‎【答案】解：（1）∵抛物线C1、C2都过点A（﹣3，0）、B（3，0），‎ ‎∴设它们的解析式为：y=a（x﹣3）（x+3）。‎ ‎∵抛物线C1还经过D（0，﹣3），∴﹣3=a（0﹣3）（0+3），解得a=。‎ ‎∴抛物线C1：y=（x﹣3）（x+3），即y=x2﹣3（﹣3≤x≤3）。‎ ‎∵抛物线C2还经过A（0，1），∴1=a（0﹣3）（0+3），a=﹣‎ ‎∴抛物线C2：y=﹣（x﹣3）（x+3），即y=﹣x2+1（﹣3≤x≤3）。‎ ‎（2）∵直线BE：y=x﹣1必过（0，﹣1），∴∠CBO=∠EBO（tan∠CBO=tan∠EBO=）。‎ ‎∵由E点坐标可知：tan∠AOE≠，即∠AOE≠∠CBO，‎ ‎∴它们的补角∠EOB≠∠CBx。‎ 若以点P、B、C为顶点的△PBC与△BOE相似，只需考虑两种情况：‎ ‎①∠CBP1=∠EBO，且OB：BE=BP1：BC，‎ 由已知和勾股定理，得OB=3，BE=，BC=。‎ ‎∴3：=BP1：，‎ 得：BP1=，OP1=OB﹣BP1=。∴P1（，0）‎ ‎②∠P2BC=∠EBO，且BC：BP2=OB：BE，即：‎ ‎：BP2=3：，得：BP2=，OP2=BP2﹣OB=。∴P2（﹣，0）．‎ 综上所述，符合条件的P点有：P1（，0）、P2（﹣，0）。‎ ‎（3）如图，作直线l∥直线BE，设直线l：y=x+b。‎ ‎①当直线l与抛物线C1只有一个交点时：‎ x+b=x2﹣3，即：x2﹣x﹣（3b+9）=0。‎ 由△=（－1）2＋4（3b+9）=0。得。‎ 此时，。‎ ‎∴该交点Q2（）。‎ 过点Q2作Q‎2F⊥BE于点F，则由BE：y=x﹣1可用相似得Q‎2F的斜率为－3，‎ 设Q‎2F：y=－3x＋m。将Q2（）代入，可得。∴Q‎2F：y=－3x。‎ 联立BE和Q‎2F，解得。∴F（）。‎ ‎∴Q2到直线 BE：y=x﹣1的距离Q‎2F：。‎ ‎②当直线l与抛物线C2只有一个交点时：x+b=﹣x2+1，即：x2+3x+9b﹣9=0。‎ 由△=32＋4（9b－9）=0。得。‎ 此时，。∴该交点Q1（）。‎ 同上方法可得Q1到直线 BE：y=x﹣1 的距离：。‎ ‎∵，‎ ‎∴符合条件的Q点为Q1（）。‎ ‎∴△EBQ的最大面积：。‎ ‎【考点】二次函数综合题，待定系数法，曲线上点的坐标与方程的关系，相似三角形的判定和性质，勾股定理，一元二次方程根的判别式，点到直线的距离，平行线的性质。‎ ‎【分析】（1）已知A、B、C、D四点坐标，利用待定系数法即可确定两函数的解析式。‎ ‎（2）根据直线BE：y=x﹣1知，该直线必过（0，﹣1）点，那么∠EBO=∠CBO，若以点P、B、C为顶点的△PBC与△BOE相似，那么夹这组对应角的对应边必成比例，先求出BC、BO、BE的长，然后分情况根据线段间的比例关系求出BP的长，进而得到OP的长，即可确定P点坐标。‎ ‎（3）△EBQ中，BE长为定值，若以BE为底，当△EBQ的面积最大时，Q到直线BE的距离最大；由于点Q可能在抛物线C1或C2上，因此两种情况都要解一下，最后通过比较得到能使△EBQ面积最大的Q点．首先作直线l∥BE，分别令直线l与抛物线C1、C2有且仅有一个交点，那么符合条件的Q点必在这两个交点中，先求出这两个交点分别到直线BE的距离，距离大者符合条件，由此可得到Q点坐标和△EBQ的面积最大值。‎ ‎18. （2012江苏连云港12分）如图，甲、乙两人分别从A(1，)、B(6，0)两点同时出发，点O为坐标原点，甲沿AO方向、乙沿BO方向均以‎4km/h的速度行驶，th后，甲到达M点，乙到达N点．‎ ‎(1)请说明甲、乙两人到达O点前，MN与AB不可能平行．‎ ‎(2)当t为何值时，△OMN∽△OBA？‎ ‎(3)甲、乙两人之间的距离为MN的长，设s＝MN2，求s与t 之间的函数关系式，并求甲、乙两人之间距离的最小值．‎ ‎【答案】解：(1)∵A坐标为(1，)，∴OA＝2，∠AOB＝60°。‎ ‎ ∵甲达到O点时间为t＝，乙达到O点的时间为t＝，‎ ‎∴甲先到达O点，所以t＝或t＝时，O、M、N三点不能连接成三角形。‎ ‎①当t＜时，OM＝2－4t，ON＝6－4t，‎ 假设MN∥AB。则△OMN∽△OAB。‎ ‎∴，解得t＝0。即在甲到达O点前，只有当t＝0时，△OMN∽△OAB。‎ ‎∴MN与AB不可能平行。‎ ‎②当＜t＜时，‎ 如图，∵∠PMN＞∠PON＞∠PAB ‎∴MN与AB不平行。‎ 综上所述，在甲、乙两人到达O点前， MN与AB不可能平行。‎ ‎(2) 由（1）知，当t≤时，△OMN不相似△OBA。‎ 当t＞时，OM＝4t －2，ON＝4t －6，‎ 由解得t＝2＞，‎ ‎∴当t＝2时，△OMN∽△OBA。‎ ‎(3)①当t≤时，如图1，过点M作MH⊥x轴，垂足为H，‎ 在Rt△MOH中，∵∠AOB＝60°，‎ ‎∴MH＝OMsin60°＝(2－4t)×＝(1－2t)，‎ OH＝0Mcos60°＝(2－4t)×＝1－2t，‎ ‎∴NH＝(6－4t)－(1－2t)＝5－2t。‎ ‎∴s＝[(1－2t)]2＋(5－2t)2＝16t2－32t＋28。‎ ‎②当＜t≤时，如图2，作MH⊥x轴，垂足为H，‎ 在Rt△MNH中，MH＝(4t－2)＝(2t－1)，‎ NH＝(4t－2)＋(6－4t)＝5－2t，‎ ‎∴s＝[(1－2t)]2＋(5－2t)2＝16t2－32t＋28。‎ ③当t＞时，同理可得s＝16t2－32t＋28。‎ 综上所述，s＝16t2－32t＋28。‎ ‎∵s＝16t2－32t＋28＝16(t－1)2＋12，‎ ‎∴当t＝1时，s有最小值为12，‎ ‎∴甲、乙两人距离最小值为（km）。‎ ‎【考点】反证法，坐标与图形性质，平行的判定和性质，相似三角形的判定和性质，三角形外角性质，勾股定理，锐角三角函数定义，特殊角的三角函数值，二次函数的最值。‎ ‎【分析】(1)用反证法说明．根据已知条件分别表示相关线段的长度，根据三角形相似得比例式说明。‎ ‎(2)根据两个点到达O点的时间不同分段讨论解答。‎ ‎(3)在不同的时间段运用相似三角形的判定和性质分别求解析式，运用函数性质解答问题。‎ ‎19. （2012江苏无锡8分）对于平面直角坐标系中的任意两点P1（x1，y1），P2（x2，y2），我们把|x1﹣x2|+|y1﹣y2|叫做P1、P2两点间的直角距离，记作d（P1，P2）．‎ ‎（1）已知O为坐标原点，动点P（x，y）满足d（O，P）=1，请写出x与y之间满足的关系式，并在所给的直角坐标系中画出所有符合条件的点P所组成的图形；‎ ‎（2）设P0（x0，y0）是一定点，Q（x，y）是直线y=ax+b上的动点，我们把d（P0，Q）的最小值叫做P0到直线y=ax+b的直角距离．试求点M（2，1）到直线y=x+2的直角距离．‎ ‎【答案】解：（1）由题意，得|x|+|y|=1。‎ 所有符合条件的点P组成的图形如图所示：‎ ‎（2）∵d（M，Q）=|x﹣2|+|y﹣1|=|x﹣2|+|x+2﹣1|=|x﹣2|+|x+1|，‎ 又∵x可取一切实数，|x﹣2|+|x+1|表示数轴上实数x所对应的点到数2和﹣1所对应的点的距离之和，其最小值为3。‎ ‎∴点M（2，1）到直线y=x+2的直角距离为3。‎ ‎【考点】新定义，一次函数综合题，绝对值与数轴的关系。‎ ‎【分析】（1）根据新定义知|x|+|y|=1，据此可以画出符合题意的图形。‎ ‎（2）根据新定义知d（M，Q）=|x﹣2|+|y﹣1|=|x﹣2|+|x+2﹣1|=|x﹣2|+|x+1|，然后由绝对值与数轴的关系可知，|x﹣2|+|x+1|表示数轴上实数x所对应的点到数2和﹣1所对应的点的距离之和，其最小值为3。‎ ‎20. （2012四川凉山8分）如图，已知直径为OA的⊙P与x轴交于O、A两点，点B、C把三等分，连接PC并延长PC交y轴于点D（0，3）．‎ （1） 求证：△POD≌△ABO；‎ （2） 若直线l：y=kx+b经过圆心P和D，求直线l的解析式 ‎【答案】（1）证明：连接PB，‎ ‎∵直径为OA的⊙P与x轴交于O、A两点，点B、C把三等分，‎ ‎∴∠APB=∠DPO=×180°=60°，∠ABO=∠POD=90°。‎ ‎∵PA=PB，∴△PAB是等边三角形。‎ ‎∴AB=PA，∠BAO=60°，‎ ‎∴AB=OP，∠BAO=∠OPD。‎ 在△POD和△ABO中，‎ ‎∵∠OPD=∠BAO， OP=BA ，∠POD=∠ABO ， ‎ ‎∴△POD≌△ABO（ASA）。‎ ‎（2）解：由（1）得△POD≌△ABO，∴∠PDO=∠AOB。‎ ‎∵∠AOB=∠APB=×60°=30°，∴∠PDO=30°。‎ ‎∴OP=OD•tan30°=3×。∴点P的坐标为：（－，0）。‎ ‎∵点P，D在直线y=kx+b上，‎ ‎∴ ，解得： 。 ‎ ‎∴直线l的解析式为：y=x+3。‎ ‎【考点】圆周角定理，全等三角形的判定，锐角三角函数定义，直线上点的坐标与方程的关系。‎ ‎【分析】（1）首先连接PB，由直径为OA的⊙P与x轴交于O、A两点，点B、C把三等分，可求得∠APB=∠DPO=60°，∠ABO=∠POD=90°，即可得△PAB是等边三角形，可得AB=OP，然后由ASA，即可判定：△POD≌△ABO。‎ ‎（2）易求得∠PDO=30°，由OP=OD•tan30°，即可求得点P的坐标，然后利用待定系数法，即可求得直线l的解析式。‎ ‎21. （2012四川巴中10分）如图，在平面直角坐标系中，一次函数的图象与y轴交于点A，‎ 与x轴交于点B，与反比例函数的图象分别交于点M，N，已知△AOB的面积为1，点M的纵坐 标为2，‎ ‎（1）求一次函数和反比例函数的解析式；‎ ‎（2）直接写出时x的取值范围。‎ ‎【答案】解：（1）∵一次函数的图象与y轴交于点A，与x轴交于点B，‎ ‎∴A（0，1），B（ ，0）。‎ ‎∵△AOB的面积为1，∴×OB×OA=1，即。∴。‎ ‎∴一次函数的解析式为y1= x+1。‎ ‎∵点M在直线y1上，∴当y=2时，x+1=2，解得x=－2。∴M的坐标为（－2，2）‎ 又∵点M在反比例函数的图象上，∴k2=－2×2=－4，‎ ‎∴反比例函数的解析式为。‎ ‎（2）当y1＞y2时，x＜－2或0＜x＜4。‎ ‎【考点】反比例函数与一次函数的交点问题，曲线上点的坐标与方程的关系。‎ ‎【分析】（1）先由一次函数的解析式求出点A与点B的坐标，再根据△AOB的面积为1，可得到k1的值，‎ 从而求出一次函数的解析式；得到点M的坐标，然后运用待定系数法即可求出反比例函数的解析式。‎ ‎（2）y1＞y2即一次函数值大于反比例函数值，只需观察一次函数的图象落在反比例函数的图象的 上方时自变量的取值范围即可，为此，先求出它们的交点坐标，再根据函数图象，可知在在点M的左边以及原点和点N之间的区间，y1＞y2： ‎ 解方程组得或 ，‎ ‎∴当y1＞y2时，x＜－2或0＜x＜4。‎ ‎22. （2012四川资阳9分）抛物线的顶点在直线上，过点F（－2，2）的直线交该抛物线于点M、N两点（点M在点N的左边），MA⊥x轴于点A，NB⊥x轴于点B．[来源:&中%国教育出^版~网@]‎ ‎（1）(3分)先通过配方求抛物线的顶点坐标（坐标可用含m的代数式表示），再求m的值；[来&源#%:^中*教网]‎ ‎（2）(3分)设点N的横坐标为a，试用含a的代数式表示点N的纵坐标，并说明NF＝NB；‎ ‎（3）(3分)若射线NM交x轴于点P，且PA×PB＝，求点M的坐标．‎ ‎【答案】解：（1）∵，∴顶点坐标为(－2 , )。‎ ‎∵顶点在直线上，@]∴－2+3=，解得。‎ ‎（2）∵点N在抛物线上，且点N的横坐标为a，‎ ‎∴点N的纵坐标为，即点N(a,)。‎ 过点F作FC⊥NB于点C，‎ 在Rt△FCN中，FC=a+2，NC=NB－CB=,‎ ‎∴ ‎ ‎。‎ 而，‎ ‎∴NF2=NB2，NF=NB。‎ ‎（3）连接AF、BF，‎ 由NF=NB，得∠NFB=∠NBF，‎ 由（2）的结论知，MF=MA，‎ ‎∴∠MAF=∠MFA。‎ ‎∵MA⊥x轴，NB⊥x轴，‎ ‎∴MA∥NB。∴∠AMF+∠BNF=180°。‎ ‎∵△MAF和△NFB的内角总和为360°，∴2∠MAF+2∠NBF=180°，∠MAF+∠NBF=90°。~国%&教*育出^版网]‎ ‎∵∠MAB+∠NBA=180°，∴∠FBA+∠FAB=90°。‎ 又∵∠FAB+∠MAF=90°，[，∴∠FBA=∠MAF=∠MFA 。‎ 又∵∠FPA=∠BPF，∴△PFA∽△PBF。‎ ‎∴，∴PF2= PA×PB＝。‎ 过点F作FG⊥x轴于点G。‎ 在Rt△PFG中，，∴PO=PG+GO=。‎ ‎∴P(－ , 0) 。‎ 设直线PF：，把点F（－2 , 2）、点P(－ , 0)代入得 ‎，解得。‎ ‎∴直线PF：。‎ 解方程，得x=－3或x=2（不合题意，舍去）。‎ 当x=－3时，，∴M（－3 , ）。‎ ‎【考点】二次函数综合题，二次函的性质，待定系数法，曲线上点的坐标与方程的关系，勾股定理，相似三角形的判定和性质。‎ ‎【分析】（1）利用配方法将二次函数整理成顶点式即可，再利用点在直线上的性质得出答案即可。‎ ‎ （2）首先利用点N在抛物线上，得出N点坐标，再利用勾股定理得出NF2=NC2+FC2，从而得出NF2=NB2，即可得出答案。‎ ‎（3）求点M的坐标，需要先求出直线PF的解析式．首先由（2）的思路得出MF=MA，然后连接AF、FB，通过证明△PFA∽△PBF，利用相关的比例线段将PA•PB的值转化为PF的值，从而求出点F的坐标和直线PF的解析式，即可得解。‎ ‎23. （2012山东菏泽10分）牡丹花会前夕，我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销．经过调查，得到如下数据：‎ 销售单价（元/件）‎ ‎…‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎60‎ ‎…‎ 每天销售量（件）‎ ‎…‎ ‎500‎ ‎400‎ ‎300‎ ‎200‎ ‎100‎ ‎…‎ ‎（1）把上表中、的各组对应值作为点的坐标，在下面的平面直角坐标系中描出相应的点，猜想与的函数关系，并求出函数关系式；‎ ‎（2）当销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？最大利润是多少？（利润=销售总价﹣成本总价）‎ ‎（3）菏泽市物价部门规定，该工艺品销售单价最高不能超过35元/件，那么销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？‎ ‎【答案】解：（1）画图如下：‎ 由图可猜想与是一次函数关系，设这个一次函数为，‎ ‎∵这个一次函数的图象经过（20，500）、（30，400）两点，‎ ‎∴，解得。‎ ‎∴函数关系式是。‎ 经验证，其它各点也在上。‎ ‎　　 （2）设工艺厂试销该工艺品每天获得的利润是W元，依题意得：‎ ‎，‎ ‎∴当时，W有最大值9000。‎ ‎　　 （3）对于函数，当时，W的值随着值的增大而增大，‎ ‎ ∴销售单价定为35元∕件时，工艺厂试销该工艺品每天获得的利润最大。‎ ‎【考点】二次函数和一次函数的应用，待定系数法，直线上点的坐标与方程的关系，二次函数的最值和增减性。‎ ‎【分析】（1）利用表中、的各组对应值作为点的坐标，在坐标系中描出即可，再取任意两点用待定系数法得出与的函数关系式，求出即可。‎ ‎（2）根据利润=销售总价-成本总价，由（1）中函数关系式得出，从而利用二次函数最值求法得出即可。‎ ‎（3）利用二次函数的增减性，结合对称轴即可得出答案。‎ ‎24. （2012山东泰安12分）如图，半径为2的⊙C与x轴的正半轴交于点A，与y轴的正半轴交于点B，点C的坐标为（1，0）．若抛物线过A、B两点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）在抛物线上是否存在点P，使得∠PBO=∠POB？若存在，求出点P的坐标；若不存在说明理由；‎ ‎（3）若点M是抛物线（在第一象限内的部分）上一点，△MAB的面积为S，求S的最大（小）值．‎ ‎【答案】解：（1）如图1，连接OB。‎ ‎∵BC=2，OC=1，∴OB=。‎ ‎∴B（0，）。‎ 将A（3，0），B（0，）代入二次函数的表达式，‎ 得 ，解得： 。‎ ‎∴抛物线的解析式为。‎ ‎（2）存在。‎ 如图2，作线段OB的垂直平分线l，与抛物线的交点即为点P。‎ ‎∵B（0，），O（0，0），‎ ‎∴直线l的表达式为．代入抛物线的表达式，‎ 得；解得。‎ ‎∴P（）。‎ ‎（3）如图3，作MH⊥轴于点H。设M（ ），‎ 则S△MAB=S梯形MBOH+S△MHA﹣S△OAB ‎=‎ ‎=。‎ ‎∵，‎ ‎∴ ‎ ‎= 。‎ ‎∴当时，取得最大值，最大值为。‎ ‎【考点】二次函数综合题，曲线上点的坐标与方程的关系，勾股定理，线段垂直平分线的性质，二次函数最值。‎ ‎【分析】（1）利用待定系数法求抛物线的解析式．因为已知A（3，0），所以需要求得B点坐标．如图1，连接OB，利用勾股定理求解。‎ ‎（2）由∠PBO=∠POB，可知符合条件的点在线段OB的垂直平分线上．如图2，OB的垂直平分线与抛物线有两个交点，因此所求的P点有两个，注意不要漏解。‎ ‎（3）如图3，作MH⊥轴于点H，构造梯形MBOH与三角形MHA，求得△MAB面积的表达式，这个表达式是关于M点横坐标的二次函数，利用二次函数的极值求得△MAB面积的最大值。‎ ‎25. （2012山东聊城12分）某电子厂商投产一种新型电子厂品，每件制造成本为18元，试销过程中发现，每月销售量y（万件）与销售单价x（元）之间的关系可以近似地看作一次函数y=﹣2x+100．（利润=售价﹣制造成本）‎ ‎（1）写出每月的利润z（万元）与销售单价x（元）之间的函数关系式；‎ ‎（2）当销售单价为多少元时，厂商每月能获得3502万元的利润？当销售单价为多少元时，厂商每月能获得最大利润？最大利润是多少？‎ ‎（3）根据相关部门规定，这种电子产品的销售单价不能高于32元，如果厂商要获得每月不低于350万元的利润，那么制造出这种产品每月的最低制造成本需要多少万元？‎ ‎【答案】解：（1）∵z=（x﹣18）y=（x﹣18）（﹣2x+100）=﹣2x2+136x﹣1800，‎ ‎ ∴z与x之间的函数解析式为z=﹣2x2+136x﹣1800。‎ ‎（2）由z=350，得350=﹣2x2+136x﹣1800，‎ 解这个方程得x1=25，x2=43。‎ ‎∴销售单价定为25元或43元时，厂商每月能获得3502万元的利润。‎ ‎∵z═﹣2x2+136x﹣1800 =﹣2（x﹣34）2+512，‎ ‎∴当销售单价为34元时，每月能获得最大利润，最大利润是512万元。‎ ‎（3）结合（2）及函数z=﹣2x2+136x﹣1800的图象（如图所示）可知，‎ 当25≤x≤43时，z≥350。‎ 又由限价32元，得25≤x≤32。‎ 根据一次函数的性质，得y=﹣2x+100中y随x的增大而减小，‎ ‎∴当x=32时，每月制造成本最低。‎ 最低成本是18×（﹣2×32+100）=648（万元）。‎ ‎∴所求每月最低制造成本为648万元。‎ ‎【考点】二次函数和一次函数的应用。‎ ‎【分析】（1）根据每月的利润z=（x﹣18）y，再把y=﹣2x+100代入即可求出z与x之间的函数解析式。‎ ‎（2）把z=350代入z=﹣2x2+136x﹣1800，解这个方程即可，将z═﹣2x2+136x﹣1800配方，得 z=﹣2（x﹣34）2+512，即可求出当销售单价为多少元时，厂商每月能获得的最大利润。‎ ‎（3）结合（2）及函数z=﹣2x2+136x﹣1800的图象即可求出当25≤x≤43时z≥350，再根据限价32元，得出25≤x≤32，最后根据一次函数y=﹣2x+100中y随x的增大而减小，即可得出当x=32时，每月制造成本最低，求出最低成本。‎ ‎26. （2012山东潍坊10分）许多家庭以燃气作为烧水做饭的燃料，节约用气是我们日常生活中非常现实的问题．某款燃气灶旋钮位置从0度到90度(如图)，燃气关闭时，燃气灶旋钮的位置为0度，旋钮角度越大，燃气流量越大，燃气开到最大时，旋钮角度为90度．为测试燃气灶旋钮在不同位置上的燃气用量，在相同条件下，选择在燃气灶旋钮的5个不同位置上分别烧开一壶水(当旋钮角度太小时，其火力不能够将水烧开，故选择旋钮角度x度的范围是18≤x≤90)，记录相关数据得到下表：‎ 旋钮角度(度)‎ ‎ 20‎ ‎ 50‎ ‎ 70‎ ‎ 80‎ ‎ 90‎ 所用燃气量(升)‎ ‎ 73‎ ‎ 67‎ ‎ 83‎ ‎ 97‎ ‎ 115‎ ‎ (1)请你从所学习过的一次函数、反比例函数和二次函数中确定哪种函数能表示所用燃气量y升与旋钮角度x度的变化规律?说明确定是这种函数而不是其它函数的理由，并求出它的解析式；‎ ‎ (2)当旋钮角度为多少时，烧开一壶水所用燃气量最少?最少是多少?‎ ‎ (3)某家庭使用此款燃气灶，以前习惯把燃气开到最大，现采用最节省燃气的旋钮角度，每月平均能节约燃气10立方米，求该家庭以前每月的平均燃气用量．‎ ‎【答案】解：（1）若设y=kx+b（k≠0），‎ 由解得 。∴y= x+77。‎ 把x=70代入得y=65≠83，∴一次函数不符合。‎ 若设（k≠0），由解得k=1460。∴ 。‎ 把x=50代入得y=29.2≠67，∴反比例函数不符合。‎ 若设y=ax2＋bx＋c，‎ 由 解得。∴y=x2 x＋97（18≤x≤90）。‎ 把x=80代入得y=97，把x=90代入得y=115，符合题意。‎ ‎∴二次函数能表示所用燃气量y升与旋钮角度x度的变化规律。‎ ‎（2）由（1）得：y=x2 x＋97=（x－40）2+65，‎ ‎∴当x=40时，y取得最小值65。‎ 答：当旋钮角度为40°时，烧开一壶水所用燃气量最少，最少为‎65升。‎ ‎ （3）由（2）及表格知，采用最节省燃气的旋钮角度40度比把燃气开到最大时烧开一壶水节约用气115－65=50（升），设该家庭以前每月平均用气量为a立方米，则由题意得：‎ ‎，解得a=23。‎ 答：该家庭以前每月平均用气量为‎23立方米。‎ ‎【考点】待定系数法，曲线上点的坐标与方程的关系，二次函数的性质。‎ ‎【分析】（1）先假设函数为一次函数，任选两点求出函数解析式，再将各点代入验证；再假设函数为二次函数，任选三求出函数解析式，再将各点代入验证 ‎（2）将（1）所求二次函数解析式，化为顶点式，转化为二次函数最值的问题。‎ ‎（3）由（2）及表格知，采用最节省燃气的旋钮角度40度比把燃气开到最大时烧开一壶水节约用气115－65=50，再设该家庭以前每月平均用气量为a立方米，据此解答即可。‎ ‎27. （2012山东济南9分）如图1，抛物线y=ax2＋bx＋3与x轴相交于点A（－3，0），B（－1，0），与y轴相交于点C，⊙O1为△ABC的外接圆，交抛物线于另一点D．‎ ‎（1）求抛物线的解析式；‎ ‎（2）求cos∠CAB的值和⊙O1的半径；‎ ‎（3）如图2，抛物线的顶点为P，连接BP，CP，BD，M为弦BD中点，若点N在坐标平面内，满足△BMN∽△BPC，请直接写出所有符合条件的点N的坐标．‎ ‎【答案】解：（1）∵抛物线y=ax2＋bx＋3与x轴相交于点A（－3，0），B（－1，0），‎ ‎∴，解得。∴抛物线的解析式为：y=x2＋4x＋3。 （2）由（1）知，抛物线解析式为：y=x2＋4x＋3，‎ ‎∵令x=0，得y=3，∴C（0，3）。‎ ‎∴OC=OA=3，则△AOC为等腰直角三角形。‎ ‎∴∠CAB=45°，∴cos∠CAB=。‎ 在Rt△BOC中，由勾股定理得：BC=。‎ 如图1所示，连接O1B、O‎1C，‎ 由圆周角定理得：∠BO‎1C=2∠BAC=90°。‎ ‎∴△BO‎1C为等腰直角三角形，‎ ‎∴⊙O1的半径O1B=。‎ ‎（3）点N的坐标为（，）或（，）。‎ ‎【考点】二次函数综合题，曲线上点的坐标与方程的关系，等腰直角三角形的性质，锐角三角函数定义，特殊角的三角函数值，圆周角定理，圆及抛物线的对称性质，相似三角形的性质，勾股定理。‎ ‎【分析】（1）利用待定系数法求出抛物线的解析式；‎ ‎（2）如答图1所示，由△AOC为等腰直角三角形，确定∠CAB=45°，从而求出其三角函数值；由 圆周角定理，确定△BO‎1C为等腰直角三角形，从而求出半径的长度。‎ ‎（3）如答图2所示，首先利用圆及抛物线的对称性求出点D坐标，从而求出点M的坐标和线段 BM的长度；点B、P、C的坐标已知，求出线段BP、BC、PC的长度；然后利用△BMN∽△BPC相似三角形比例线段关系，求出线段BN和MN的长度；最后利用勾股定理，列出方程组，求出点N的坐标。‎ ‎∵抛物线y=x2＋4x＋3=（x＋2）2－1，‎ ‎∴顶点P坐标为（－2，－1），对称轴为x= －2。‎ 又∵A（－3，0），B（－1，0），可知点A、B关于对称轴x=2对称。‎ 如图2所示，由圆及抛物线的对称性可知：点D、点C（0，3）关于对称轴对称。‎ ‎∴D（－4，3）。‎ 又∵点M为BD中点，B（－1，0），∴M（）。‎ ‎∴BM=。‎ 在△BPC中，B（－1，0），P（－2，－1），C（0，3），‎ 由勾股定理得：BP=，BC=，PC=。‎ ‎∵△BMN∽△BPC，‎ ‎∴，即。‎ 解得：BN=，MN。‎ 设N（x，y），由勾股定理可得：‎ ‎，解得，，。‎ ‎∴点N的坐标为（，）或（，）。‎ ‎28. （2012山东德州10分）现从A，B向甲、乙两地运送蔬菜，A，B两个蔬菜市场各有蔬菜14吨，其中甲地需要蔬菜15吨，乙地需要蔬菜13吨，从A到甲地运费50元/吨，到乙地30元/吨；从B地到甲运费60元/吨，到乙地45元/吨．‎ ‎（1）设A地到甲地运送蔬菜x吨，请完成下表：‎ 运往甲地（单位：吨）‎ 运往乙地（单位：吨）‎ A x B ‎（2）设总运费为W元，请写出W与x的函数关系式 ‎（3）怎样调运蔬菜才能使运费最少？‎ ‎【答案】解：（1）完成填表：‎ 运往甲地（单位：吨）‎ 运往乙地（单位：吨）‎ A x ‎14﹣x B ‎15﹣x x﹣1‎ ‎（2）W=50x＋30（14－x）＋60（15－x）＋45（x－1），‎ 整理得，W=5x＋1275。 ‎ ‎（3）∵A，B到两地运送的蔬菜为非负数，‎ ‎∴，解不等式组，得：1≤x≤14。‎ 在W=5x+1275中，W随x增大而增大，‎ ‎∴当x最小为1时，W有最小值 1280元。‎ ‎【考点】一次函数和一元一次不等式组的应用。‎ ‎【分析】（1）根据题意A，B两个蔬菜市场各有蔬菜14吨，其中甲地需要蔬菜15吨，乙地需要蔬菜13吨，可得解。‎ ‎（2）根据从A到甲地运费50元/吨，到乙地30元/吨；从B地到甲运费60元/吨，到乙地45元/吨可列出总费用，从而可得出答案。‎ ‎（3）求出x的取值范围，利用w与x之间的函数关系式，求出函数最值即可。‎ ‎29. （2012浙江舟山14分）在平面直角坐标系xOy中，点P是抛物线：y=x2上的动点（点在第一象限内）．连接 OP，过点0作OP的垂线交抛物线于另一点Q．连接PQ，交y轴于点M．作PA丄x轴于点A，QB丄x轴于点B．设点P的横坐标为m．‎ ‎（1）如图1，当m=时，‎ ‎①求线段OP的长和tan∠POM的值；‎ ‎②在y轴上找一点C，使△OCQ是以OQ为腰的等腰三角形，求点C的坐标；‎ ‎（2）如图2，连接AM、BM，分别与OP、OQ相交于点D、E．‎ ‎①用含m的代数式表示点Q的坐标；‎ ‎②求证：四边形ODME是矩形．‎ ‎【答案】解：（1）①把x=代入 y=x2，得 y=2，∴P（，2），∴OP=。‎ ‎∵PA丄x轴，∴PA∥MO．∴。‎ ‎②设 Q（n，n2），∵tan∠QOB=tan∠POM，∴．∴。‎ ‎∴Q（）。∴OQ=。‎ ‎∴当 OQ=OC 时，则C1（0，），C2（0，－）。‎ 当 OQ=CQ 时，则 C3（0，1）。‎ ‎（2）①∵点P的横坐标为m，∴P（m，m2）。设 Q（n，n2），‎ ‎∵△APO∽△BOQ，∴。∴，得。‎ ‎∴Q（）。‎ ‎②设直线PO的解析式为：y=kx+b，把P（m，m2）、Q（）代入，得：‎ ‎，解得b=1。∴M（0，1）。‎ ‎∵，∠QBO=∠MOA=90°，∴△QBO∽△MOA。‎ ‎∴∠MAO=∠QOB，∴QO∥MA。‎ 同理可证：EM∥OD。‎ 又∵∠EOD=90°，∴四边形ODME是矩形。‎ ‎【考点】二次函数综合题，待定系数法，曲线上点的坐标与方程的关系，勾股定理，平行的判定和性质，锐角三角函数定义，等腰三角形的性质，相似三角形的判定和性质，矩形的判定。‎ ‎【分析】（1）①已知m的值，代入抛物线的解析式中可求出点P的坐标；由此确定PA、OA的长，通过解直角三角形易得出结论。‎ ‎②题目要求△OCQ是以OQ为腰的等腰三角形，所以分QO=OC、QC=QO两种情况来判断：‎ QO=QC时，Q在线段OC的垂直平分线上，Q、O的纵坐标已知，C点坐标即可确定；‎ QO=OC时，先求出OQ的长，那么C点坐标可确定。‎ ‎（2）①由∠QOP=90°，易求得△QBO∽△MOA，通过相关的比例线段来表示出点Q的坐标。‎ ‎②在四边形ODME中，已知了一个直角，只需判定该四边形是平行四边形即可，那么可通过证明两组对边平行来得证。‎ ‎30. （2012浙江舟山14分）在平面直角坐标系xOy中，点P是抛物线：y=x2上的动点（点在第一象限内）．连接 OP，过点0作OP的垂线交抛物线于另一点Q．连接PQ，交y轴于点M．作PA丄x轴于点A，QB丄x轴于点B．设点P的横坐标为m．‎ ‎（1）如图1，当m=时，‎ ‎①求线段OP的长和tan∠POM的值；‎ ‎②在y轴上找一点C，使△OCQ是以OQ为腰的等腰三角形，求点C的坐标；‎ ‎（2）如图2，连接AM、BM，分别与OP、OQ相交于点D、E．‎ ‎①用含m的代数式表示点Q的坐标；‎ ‎②求证：四边形ODME是矩形．‎ ‎【答案】解：（1）①把x=代入 y=x2，得 y=2，∴P（，2），∴OP=。‎ ‎∵PA丄x轴，∴PA∥MO．∴。‎ ‎②设 Q（n，n2），∵tan∠QOB=tan∠POM，∴．∴。‎ ‎∴Q（）。∴OQ=。‎ ‎∴当 OQ=OC 时，则C1（0，），C2（0，－）。‎ 当 OQ=CQ 时，则 C3（0，1）。‎ ‎（2）①∵点P的横坐标为m，∴P（m，m2）。设 Q（n，n2），‎ ‎∵△APO∽△BOQ，∴。∴，得。‎ ‎∴Q（）。‎ ‎②设直线PO的解析式为：y=kx+b，把P（m，m2）、Q（）代入，得：‎ ‎，解得b=1。∴M（0，1）。‎ ‎∵，∠QBO=∠MOA=90°，∴△QBO∽△MOA。‎ ‎∴∠MAO=∠QOB，∴QO∥MA。‎ 同理可证：EM∥OD。‎ 又∵∠EOD=90°，∴四边形ODME是矩形。‎ ‎【考点】二次函数综合题，待定系数法，曲线上点的坐标与方程的关系，勾股定理，平行的判定和性质，锐角三角函数定义，等腰三角形的性质，相似三角形的判定和性质，矩形的判定。‎ ‎【分析】（1）①已知m的值，代入抛物线的解析式中可求出点P的坐标；由此确定PA、OA的长，通过解直角三角形易得出结论。‎ ‎②题目要求△OCQ是以OQ为腰的等腰三角形，所以分QO=OC、QC=QO两种情况来判断：‎ QO=QC时，Q在线段OC的垂直平分线上，Q、O的纵坐标已知，C点坐标即可确定；‎ QO=OC时，先求出OQ的长，那么C点坐标可确定。‎ ‎（2）①由∠QOP=90°，易求得△QBO∽△MOA，通过相关的比例线段来表示出点Q的坐标。‎ ‎②在四边形ODME中，已知了一个直角，只需判定该四边形是平行四边形即可，那么可通过证明两组对边平行来得证。‎ ‎31. （2012浙江宁波12分）如图，二次函数y=ax2+bx+c的图象交x轴于A（﹣1，0），B（2，0），交y轴于C（0，﹣2），过A，C画直线．‎ ‎（1）求二次函数的解析式；‎ ‎（2）点P在x轴正半轴上，且PA=PC，求OP的长；‎ ‎（3）点M在二次函数图象上，以M为圆心的圆与直线AC相切，切点为H．‎ ‎①若M在y轴右侧，且△CHM∽△AOC（点C与点A对应），求点M的坐标；‎ ‎②若⊙M的半径为，求点M的坐标．‎ ‎【答案】解：（1）∵二次函数y=ax2+bx+c的图象交x轴于A（﹣1，0），B（2，0）‎ ‎∴设该二次函数的解析式为：y=a（x+1）（x﹣2），‎ ‎ 将x=0，y=﹣2代入，得﹣2=a（0+1）（0﹣2），解得a=1。‎ ‎∴抛物线的解析式为y=（x+1）（x﹣2），即y=x2﹣x﹣2。‎ ‎（2）设OP=x，则PC=PA=x+1，‎ 在Rt△POC中，由勾股定理，得x2+22=（x+1）2，‎ 解得，x=，即OP=。‎ ‎（3）①∵△CHM∽△AOC，∴∠MCH=∠CAO。‎ ‎（i）如图1，当H在点C下方时，‎ ‎∵∠MCH=∠CAO，∴CM∥x轴，∴yM=﹣2。‎ ‎∴x2﹣x﹣2=﹣2，解得x1=0（舍去），x2=1。‎ ‎∴M（1，﹣2）。‎ ‎（ii）如图2，当H在点C上方时，‎ ‎∵∠M′CH=∠CAO，∴PA=PC。‎ 由（2）得，M′为直线CP与抛物线的另一交点，‎ 设直线CM′的解析式为y=kx﹣2，‎ 把P（，0）的坐标代入，得k﹣2=0，解得k=。‎ ‎∴y=x﹣2。‎ 由x﹣2=x2﹣x﹣2，解得x1=0（舍去），x2=。此时y=×。‎ ‎∴M′（）。‎ ‎②在x轴上取一点D，如图3，过点D作DE⊥AC于点E，使DE=，‎ 在Rt△AOC中，AC=。‎ ‎∵∠COA=∠DEA=90°，∠OAC=∠EAD，‎ ‎∴△AED∽△AOC，‎ ‎∴，即，解得AD=2。‎ ‎∴D（1，0）或D（﹣3，0）。‎ 过点D作DM∥AC，交抛物线于M，如图 则直线DM的解析式为：y=﹣2x+2或y=﹣2x﹣6。‎ 当﹣2x﹣6=x2﹣x﹣2时，即x2+x+4=0，方程无实数根，‎ 当﹣2x+2=x2﹣x﹣2时，即x2+x﹣4=0，解得。 ‎ ‎∴点M的坐标为（）或（）。‎ ‎【考点】二次函数综合题，待定系数法，曲线上点的坐标与方程的关系，勾股定理，平行的判定和性质，相似三角形的判定和性质，解一元二次方程。‎ ‎【分析】（1）根据与x轴的两个交点A、B的坐标，故设出交点式解析式，然后把点C的坐标代入计算求出a的值，即可得到二次函数解析式。‎ ‎ （2）设OP=x，然后表示出PC、PA的长度，在Rt△POC中，利用勾股定理列式，然后解方程即可。‎ ‎（3）①根据相似三角形对应角相等可得∠MCH=∠CAO，然后分（i）点H在点C下方时，利用同位角相等，两直线平行判定CM∥x轴，从而得到点M的纵坐标与点C的纵坐标相同，是-2，代入抛物线解析式计算即可；（ii）点H在点C上方时，根据（2）的结论，点M为直线PC与抛物线的另一交点，求出直线PC的解析式，与抛物线的解析式联立求解即可得到点M的坐标。‎ ‎②在x轴上取一点D，过点D作DE⊥AC于点E，可以证明△AED和△AOC相似，根据相似三角形对应边成比例列式求解即可得到AD的长度，然后分点D在点A的左边与右边两种情况求出OD的长度，从而得到点D的坐标，再作直线DM∥AC，然后求出直线DM的解析式，与抛物线解析式联立求解即可得到点M的坐标。‎ ‎32. （2012浙江绍兴12分）把一边长为‎40cm的正方形硬纸板，进行适当的剪裁，折成一个长方形盒子（纸板的厚度忽略不计）。‎ ‎（1）如图，若在正方形硬纸板的四角各剪一个同样大小的正方形，将剩余部分折成一个无盖的长方形盒子。‎ ‎①要使折成的长方形盒子的底面积为‎484cm2，那么剪掉的正方形的边长为多少？‎ ‎②折成的长方形盒子的侧面积是否有最大值？如果有，求出这个最大值和此时剪掉的正方形的边长；如果没有，说明理由。‎ ‎（2）若在正方形硬纸板的四周剪掉一些矩形（即剪掉的矩形至少有一条边在正方形硬纸板的边上），将剩余部分折成一个有盖的长方形盒子，若折成的一个长方形盒子的表面积为‎550cm2，求此时长方形盒子的长、宽、高（只需求出符合要求的一种情况）。‎ ‎【答案】解：（1）①设剪掉的正方形的边长为xcm。‎ 则（40－2x）2=484，解得（不合题意，舍去），。‎ ‎∴剪掉的正方形的边长为‎9cm。‎ ‎②侧面积有最大值。‎ 设剪掉的正方形的边长为xcm，盒子的侧面积为ycm2，‎ 则y与x的函数关系为：，‎ ‎∴x=10时，y最大=800。‎ 即当剪掉的正方形的边长为‎10cm时，长方形盒子的侧面积最大为‎800cm2。‎ ‎（2）在如图的一种剪裁图中，设剪掉的正方形的边长为xcm。‎ 则 ，‎ 解得：（不合题意，舍去），。‎ ‎∴剪掉的正方形的边长为‎15cm。‎ 此时长方体盒子的长为‎15cm，宽为‎10cm，高为‎5cm。‎ ‎【考点】二次函数的应用，一元二次方程的应用。‎ ‎【分析】（1）①假设剪掉的正方形的边长为xcm，根据题意得出（40－2x）2=484，求出即可 ‎ ②假设剪掉的正方形的边长为xcm，盒子的侧面积为ycm2，则y与x的函数关系为：y=4（40-2x）x，利用二次函数最值求出即可。‎ ‎（2）假设剪掉的正方形的边长为xcm，利用折成的一个长方形盒子的表面积为‎550cm2，得出等式方程求出即可。‎ ‎33. （2012浙江温州12分）温州享有“中国笔都”之称，其产品畅销全球，某制笔企业欲将件产品运往A,B,C三地销售，要求运往C地的件数是运往A地件数的2倍，各地的运费如图所示。设安排件产品运往A地。‎ ‎（1）当时，‎ ‎①根据信息填表：‎ A地 B地 C地 合计 产品件数（件）‎ ‎200‎ 运费（元）‎ ‎30‎ ‎②若运往B地的件数不多于运往C地的件数，总运费不超过4000元，则有哪几种运输方案？‎ ‎（2）若总运费为5800元，求的最小值。‎ ‎【答案】解：（1）①根据信息填表 A地 B地 C地 合计 产品件数（件）‎ ‎200‎ 运费（元）‎ ‎30‎ ‎②由题意，得 ，解得40≤x≤。‎ ‎∵x为整数，∴x=40或41或42。‎ ‎∴有三种方案，分别是 ‎（i）A地40件，B地80件，C地80件；‎ ‎ （ii）A地41件，B地77件，C地82件；‎ ‎ （iii）A地42件，B地74件，C地84件。 ‎ ‎（2）由题意，得30x+8（n－3x）+50x=5800，整理，得n=725－7x．‎ ‎∵n－3x≥0，∴x≤72.5。‎ 又∵x≥0，∴0≤x≤72.5且x为整数。‎ ‎∵n随x的增大而减少，∴当x=72时，n有最小值为221。‎ ‎【考点】一次函数的应用，一元一次不等式组的应用。‎ ‎【分析】（1）①运往B地的产品件数=总件数n－运往A地的产品件数－运往B地的产品件数；运费=‎ 相应件数×一件产品的运费。‎ ‎②根据运往B地的件数不多于运往C地的件数，总运费不超过4000元列出不等式组，求得整数解的个数即可。‎ ‎（2）总运费=A产品的运费+B产品的运费+C产品的运费，从而根据函数的增减性得到的x的取值求得n的最小值即可。‎ ‎34. （2012浙江台州12分）某汽车在刹车后行驶的距离s（单位：米）与时间t（单位：秒）之间的关系得部分数据如下表：‎ 时间t（秒）‎ ‎0‎ ‎0.2‎ ‎0.4‎ ‎0.6‎ ‎0.8‎ ‎1.0‎ ‎1.2‎ ‎…‎ 行驶距离s（米）‎ ‎0‎ ‎2.8‎ ‎5.2‎ ‎7.2‎ ‎8.8‎ ‎10‎ ‎10.8‎ ‎…‎ ‎（1）根据这些数据在给出的坐标系中画出相应的点；‎ ‎（2）选择适当的函数表示s与t之间的关系，求出相应的函数解析式；‎ ‎（3）①刹车后汽车行驶了多长距离才停止？‎ ‎②当t分别为t1，t2（t1＜t2）时，对应s的值分别为s1，s2，请比较与的大小，并解释比较结果的实际意义．‎ ‎【答案】解：（1）描点图所示： ‎ ‎（2）由散点图可知该函数为二次函数。设二次函数的解析式为：s=at2＋bt＋c，‎ ‎∵抛物线经过点（0，0），∴c=0。‎ 又由点（0.2，2.8），（1，10）可得：‎ ‎，解得：。‎ 经检验，其余各点均在s=－5t2+15t上。‎ ‎∴二次函数的解析式为：。‎ ‎（3）①汽车刹车后到停止时的距离即汽车滑行的最大距离。‎ ‎ ∵，∴当t=时，滑行距离最大，为。‎ 因此，刹车后汽车行驶了米才停止。 ‎ ‎②∵，∴。‎ ‎∴。‎ ‎∵t1＜t2，∴。∴。‎ 其实际意义是刹车后到t2时间内的平均速到t1时间内的度小于刹车后平均速度。‎ ‎【考点】二次函数综合题，待定系数法，曲线上点的坐标与方程的关系，二次函数的性质和应用，不等式的应用。‎ ‎【分析】（1）描点作图即可。‎ ‎（2）首先判断函数为二次函数。用待定系数法，由所给的任意三点即可求出函数解析式。‎ ‎（3）将函数解析式表示成顶点式（或用公式求），即可求得答案。‎ ‎（4）求出与，用差值法比较大小。‎