威海市2010年初中升学考试数学试题及答案 11页

绝密★启用前 试卷类型：A ‎ 威海市二○一○年初中升学考试 ‎ 数 学 ‎ 亲爱的同学： ‎ 你好！答题前，请仔细阅读以下说明： ‎ ‎1．本试卷共10页，分第 I 卷和第 II 卷两部分．第 I 卷（1－2页）为选择题，第 II 卷（3－10页）为非选择题．试卷满分120分．考试时间120分钟． ‎ ‎2．请清点试卷，并将答题卡和第Ⅱ卷密封线内的考生信息填写完整． ‎ ‎3．第Ⅰ卷的答案用2B铅笔涂在答题卡上．第Ⅱ卷的答案用蓝色或黑色钢笔、圆珠笔填写在试卷上．不要求保留精确度的题目，计算结果保留准确值． ‎ 希望你能愉快地度过这120分钟，祝你成功！ ‎ 第 I 卷 （选择题，共36分） ‎ 一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一个是正确的．每小题选对得3分，选错、不选或多选，均不得分） ‎ ‎1．据统计，截止到‎5月31日上海世博会累计入园人数803.27万人．803.27万这个数字（保留两位有效数字）用科学记数法表示为 ‎ A．8.0×102 B. 8.03×‎102 ‎‎ C. 8.0×106 D. 8.03×106 ‎ ‎2．如图，在△ABC中，∠C＝90°．若BD∥AE，∠DBC＝20°，则∠CAE的度数是 A B C D E A．40° ‎ B．60° ‎ C．70° ‎ D．80° ‎ ‎3．计算的结果是 ‎ A．-2 B．‎-1 ‎ C．2 D．3 ‎ ‎4．下列运算正确的是 ‎ A． B． ‎ C． D． ‎ ‎5．一个圆锥的底面半径为6㎝，圆锥侧面展开图扇形的圆心角为240°，则圆锥的母线长为 ‎ A．9㎝ B．12㎝ C．15㎝ D．18㎝ ‎ ‎6．化简的结果是 ‎ A． B． C． D． ‎ 左视图 主视图 俯视图 ‎7．右图是由几个相同的小正方体搭成的几何体的三视图， ‎ 则搭成这个几何体的小正方体的个数是 ‎ A．5 B．6 ‎ C．7 D．8 ‎ ‎8．已知，则a2－b2－2b的值为 ‎ A．4 B．‎3 ‎‎ ‎ C．1 D．0 ‎ A D B E ‎9．如图，在△ABC中，D，E分别是边AC，AB的中点， ‎ 连接BD．若BD平分∠ABC，则下列结论错误的是 ‎ A．BC＝2BE ‎ B．∠A＝∠EDA ‎ C C．BC＝2AD ‎ D．BD⊥AC ‎ C A B D O ‎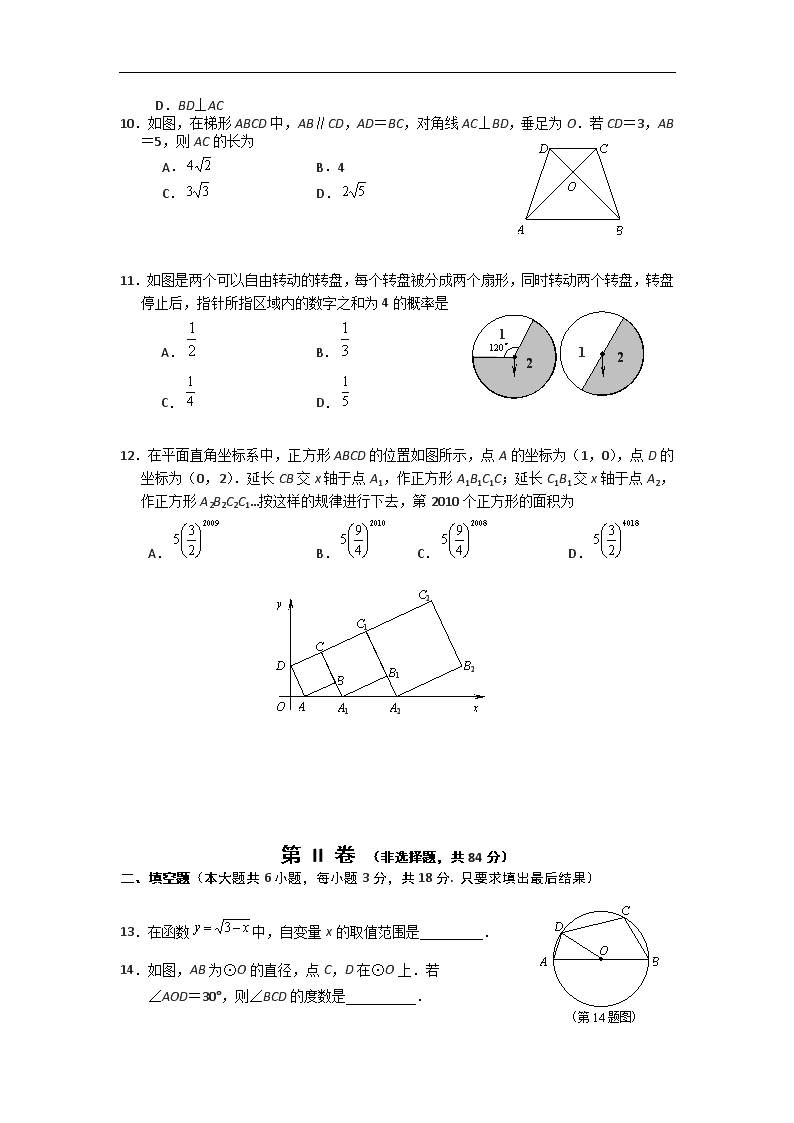10．如图，在梯形ABCD中，AB∥CD，AD＝BC，对角线AC⊥BD，垂足为O．若CD＝3，AB＝5，则AC的长为 ‎ A． B．4 ‎ C． D． ‎ ‎120°‎ ‎1‎ ‎2‎ ‎1‎ ‎2‎ ‎11．如图是两个可以自由转动的转盘，每个转盘被分成两个扇形，同时转动两个转盘，转盘停止后，指针所指区域内的数字之和为4的概率是 ‎ A． B． ‎ C． D． ‎ ‎12．在平面直角坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2）．延长CB交x轴于点A1，作正方形A1B‎1C1C；延长C1B1交x轴于点A2，作正方形A2B‎2C2C1…按这样的规律进行下去，第2010个正方形的面积为 ‎ A． B． C． D．‎ O A B C D A1‎ B1‎ C1‎ A2‎ C2‎ B2‎ x y ‎ ‎ 第 II 卷 （非选择题，共84分） ‎ 二、填空题（本大题共6小题，每小题3分，共18分. 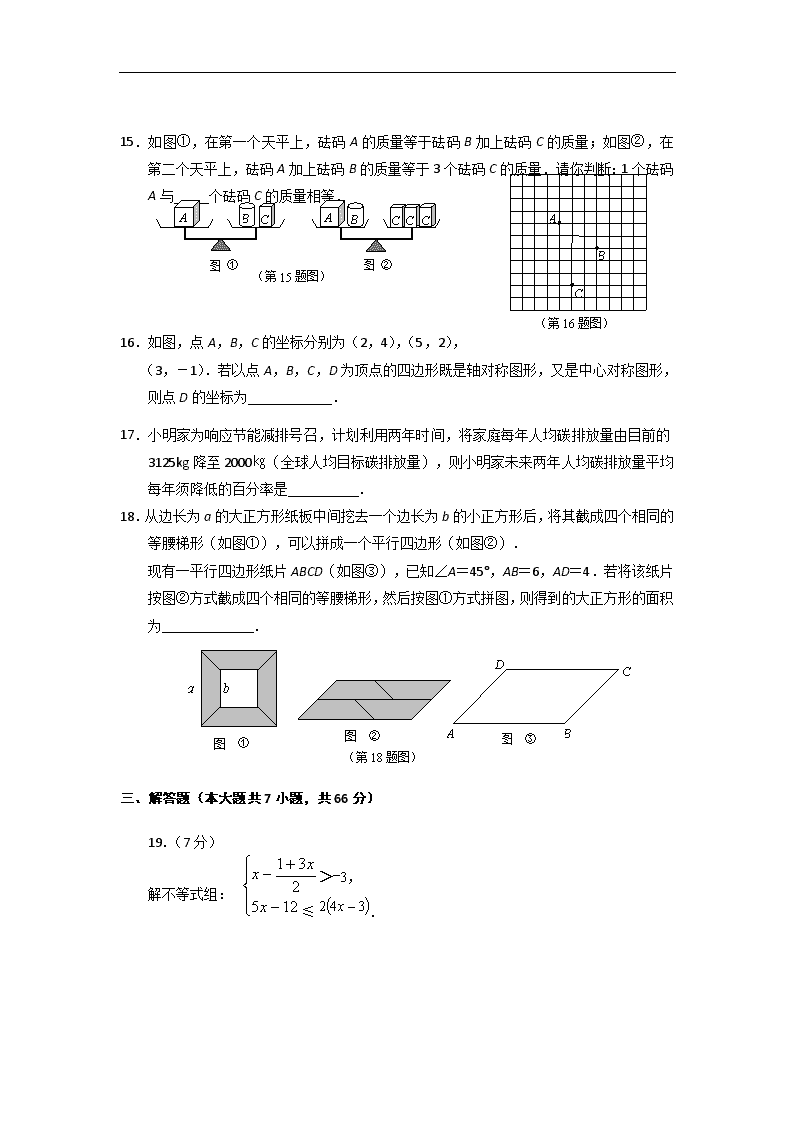只要求填出最后结果） ‎ ‎﹙第14题图﹚‎ A B D O C ‎13．在函数中，自变量x的取值范围是 ．‎ ‎14．如图，AB为⊙O的直径，点C，D在⊙O上．若 ‎∠AOD＝30°，则∠BCD的度数是 ． ‎ ‎（第15题图）‎ 图 ①‎ A C B 图 ②‎ B A C C C A B C ‎（第16题图）‎ ‎15．如图①，在第一个天平上，砝码A的质量等于砝码B加上砝码C的质量；如图②，在第二个天平上，砝码A加上砝码B的质量等于3个砝码C的质量．请你判断：1个砝码A与 个砝码C的质量相等． ‎ ‎16．如图，点A，B，C的坐标分别为（2，4），（5，2），‎ ‎（3，－1）．若以点A，B，C，D为顶点的四边形既是轴对称图形，又是中心对称图形，则点D的坐标为 ． ‎ ‎17．小明家为响应节能减排号召，计划利用两年时间，将家庭每年人均碳排放量由目前的‎3125kg降至2000㎏﹙全球人均目标碳排放量﹚，则小明家未来两年人均碳排放量平均每年须降低的百分率是 ． ‎ ‎18．从边长为a的大正方形纸板中间挖去一个边长为b的小正方形后，将其截成四个相同的等腰梯形﹙如图①﹚，可以拼成一个平行四边形﹙如图②﹚． ‎ 现有一平行四边形纸片ABCD﹙如图③﹚，已知∠A＝45°，AB＝6，AD＝4．若将该纸片按图②方式截成四个相同的等腰梯形，然后按图①方式拼图，则得到的大正方形的面积为 ． ‎ 图 ②‎ 图 ①‎ a b A 图 ③‎ B C D ‎（第18题图）‎ 三、解答题（本大题共7小题，共66分） ‎ ‎19．（7分） ‎ ‎＞-3， ‎ ‎≤. ‎ 解不等式组：‎ ‎ ‎ ‎ ‎ ‎20．（7分） ‎ 某市从今年1月1日起调整居民用天燃气价格，每立方米天燃气价格上涨25%．小颖家去年12月份的燃气费是96元．今年小颖家将天燃气热水器换成了太阳能热水器，5月份的用气量比去年12月份少‎10m³‎，5月份的燃气费是90元．求该市今年居民用气的价格．‎ ‎21．（9分） ‎ ‎23‎ 人数 ‎0‎ ‎2‎ ‎4‎ ‎6‎ ‎12‎ ‎8‎ ‎10‎ ‎14‎ ‎22‎ ‎24‎ ‎25‎ ‎26‎ ‎27‎ ‎28‎ ‎29‎ ‎30‎ 分数 某校为了解学生“体育大课间”的锻炼效果，中考体育测试结束后，随机从学校720名考生中抽取部分学生的体育测试成绩绘制了条形统计图．试根据统计图提供的信息，回答下列问题： ‎ ‎（1）共抽取了 名学生的体育测试成绩进行统计． ‎ ‎（2）随机抽取的这部分学生中男生体育成绩的平均数是 ，众数是 ；女生体育成绩的中位数是 ． ‎ ‎（3）若将不低于27分的成绩评为优秀，估计这720名考生中，成绩为优秀的学生大约是多少？ ‎ ‎ ‎ ‎22．（10分） ‎ 如图，一次函数的图象与反比例函数的图象交于点A﹙-2，-5﹚，‎ O A B C x y D C﹙5，n﹚，交y轴于点B，交x轴于点D． ‎ ‎(1) 求反比例函数和一次函数的表达式； ‎ ‎(2) 连接OA，OC．求△AOC的面积． ‎ ‎ ‎ ‎23．（10分） ‎ C A B D O F E 如图，在□ABCD中，∠DAB＝60°，AB＝15㎝．已知⊙O的半径等于3㎝，AB，AD分别与⊙O相切于点E，F．⊙O在□ABCD内沿AB方向滚动，与BC边相切时运动停止．试求⊙O滚过的路程． ‎ ‎24．（11分） ‎ A1‎ B1‎ C1‎ A B C ‎（图①） ‎ 如图①，将一张矩形纸片对折，然后沿虚线剪切，得到两个（不等边）三角形纸片△ABC，△A1B‎1C1． ‎ A B(A1)‎ C B1‎ C1‎ 图 ②‎ E ‎﹙1﹚将△ABC，△A1B‎1C1如图②摆放，使点A1与B重合，点B1在AC边的延长线上，连接CC1交BB1于点E．求证：∠B‎1C1C＝∠B1BC． ‎ A1‎ C1‎ C A B(B1)‎ 图 ③‎ F ‎﹙2﹚若将△ABC，△A1B‎1C1如图③摆放，使点B1与B重合，点A1在AC边的延长线上，连接CC1交A1B于点F．试判断∠A‎1C1C与∠A1BC是否相等，并说明理由． ‎ ‎﹙3﹚写出问题﹙2﹚中与△A1FC相似的三角形 ． ‎ ‎ ‎ ‎25.（12分） ‎ ‎（1）探究新知：‎ ‎①如图，已知AD∥BC，AD＝BC，点M，N是直线CD上任意两点．‎ A B D C M N 图 ①‎ 求证：△ABM与△ABN的面积相等． ‎ ‎②如图，已知AD∥BE，AD＝BE，AB∥CD∥EF，点M是直线CD上任一点，点G是直线EF上任一点．试判断△ABM与△ABG的面积是否相等，并说明理由． ‎ C 图 ②‎ A B D M F E G ‎（2）结论应用： ‎ 如图③，抛物线的顶点为C（1，4），交x轴于点A（3，0），交y轴于点D．试探究在抛物线上是否存在除点C以外的点E，使得△ADE与△ACD的面积相等？ 若存在，请求出此时点E的坐标，若不存在，请说明理由． ‎ ‎﹙友情提示：解答本问题过程中，可以直接使用“探究新知”中的结论．﹚ ‎ A 图 ③‎ C D B O x y A 备用图 C D B O x y 参考解答及评分意见 ‎ 评卷说明： ‎ ‎1．第一大题（选择题）和第二大题（填空题）的每小题，只有满分和零分两个评分档，不给中间分． ‎ ‎2．第三大题（解答题）每小题的解答中所对应的分数，是指考生正确解答到该步骤所应得的累计分数．部分试题有多种解法，对考生的其他解法，请参照评分意见进行评分．‎ ‎3．如果考生在解答的中间过程出现计算错误，但并没有改变试题的实质和难度，其后续部分酌情给分，但最多不超过正确解答分数的一半；若出现严重的逻辑错误，后续部分就不再给分． ‎ 一、选择题（本大题共12小题，每小题3分，共36分） ‎ 题 号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答 案 C C B D A B A C C A B D ‎ 二、填空题（本大题共6小题，每小题3分，共18分） ‎ ‎13．x≤3； 14．105°； 15．2； 16．﹙0，1﹚； 17．20%； 18．． ‎ 三、解答题（本大题共7小题, 共66分） ‎ ‎19.（本小题满分7分） ‎ 解：‎ 解不等式①，得x＜5． ………………………………………………………………3分 解不等式②，得x≥-2． ………………………………………………………………6分 因此，原不等式组的解集为-2≤x＜5． ………………………………………………7分 ‎20．（本小题满分7分）‎ 解：设该市去年居民用气的价格为x元/ m³，则今年的价格为(1+25%)x元/ m³．……1分 根据题意，得 ． …………………………………………………3分 解这个方程，得x＝2.4． …………………………………………………………………6分 经检验，x＝2.4是所列方程的根． 2.4×(1+25%)＝3 (元)． ‎ 所以，该市今年居民用气的价格为3元/ m³． ………………………………………7分 ‎21．（本小题满分9分） ‎ ‎﹙1﹚80； …………………………………………………………………………………3分 ‎ ‎﹙2﹚26.4， 27， 27； ………………………………………………﹙每空1分﹚6分 ‎﹙3﹚﹙人﹚． ……………………………………9分 ‎22．（本小题满分10分） ‎ 解：(1)∵ 反比例函数的图象经过点A﹙-2，-5﹚， ‎ ‎∴ m=(-2)×( -5)＝10． ‎ ‎ ∴ 反比例函数的表达式为． ……………………………………………………2分 ‎ ∵ 点C﹙5，n﹚在反比例函数的图象上， ‎ ‎ ∴ ． ‎ ‎∴ C的坐标为﹙5，2﹚． ……………………………………………………………3分 ‎∵ 一次函数的图象经过点A，C，将这两个点的坐标代入，得 ‎ ‎ 解得 …………………………………………………5分 ‎ ∴ 所求一次函数的表达式为y＝x-3． …………………………………………………6分 ‎(2) ∵ 一次函数y=x-3的图像交y轴于点B，‎ ‎∴ B点坐标为﹙0，-3﹚． …………………………………………………………7分 ‎∴ OB＝3． ‎ ‎∵ A点的横坐标为-2，C点的横坐标为5， ‎ ‎∴ S△AOC= S△AOB+ S△BOC=． …………10分 C A B D O F E M N O ‎23．（本小题满分10分） ‎ 解：连接OE，OA．……………………1分 ‎∵ AB，AD分别与⊙O相切于点E，F．‎ ‎∴ OE⊥AB，OE=3㎝．………………2分 ‎∵ ∠DAB＝60°， ‎ ‎∴ ∠OAE＝30°． ……………………3分 在Rt△AOE中，AE=㎝． …………………………………5分 ‎∵ AD∥BC，∠DAB＝60°， ‎ ‎∴ ∠ABC＝120°． ………………………………………………………………6分 设当运动停止时，⊙O与BC，AB分别相切于点M，N，连接ON，OB． ………7分 同理可得 BN=㎝. ……………………………………………………………9分 ‎∴ ㎝． ‎ ‎∴ ⊙O滚过的路程为㎝． ……………………………………………10分 ‎24．（本小题满分11分） ‎ ‎（1）证明：由题意，知△ABC≌△A1B‎1C1， ‎ ‎∴ AB= A1B1，BC1=AC，∠2=∠7，∠A=∠1． ‎ ‎∴ ∠3=∠A=∠1． ………………………………………………………………1分 ‎ A B(A1)‎ C B1‎ C1‎ 图 ② ‎ E ‎1‎ ‎4‎ ‎3‎ ‎2‎ ‎5‎ ‎6‎ ‎7‎ ‎∴ BC1∥AC． ‎ ‎∴ 四边形ABC‎1C是平行四边形． ………………2分 ‎∴ AB∥CC1． ‎ ‎∴ ∠4=∠7=∠2． …………………………………3分 ‎∵ ∠5=∠6，‎ ‎∴ ∠B‎1C1C＝∠B1BC．……………………………4分 ‎﹙2﹚∠A‎1C1C =∠A1BC． …………………………5分 A1‎ C1‎ C A B(B1)‎ 图 ③‎ F ‎3‎ ‎6‎ ‎4‎ ‎5‎ ‎1‎ ‎2‎ ‎7‎ ‎8‎ 理由如下：由题意，知△ABC≌△A1B‎1C1，‎ ‎∴ AB= A1B1，BC1=BC，∠1=∠8，∠A=∠2． ‎ ‎∴ ∠3=∠A，∠4=∠7． ………………………6分 ‎∵ ∠1＋∠FBC=∠8＋∠FBC，‎ ‎∴ ∠C1BC＝∠A1BA． …………………………7分 ‎∵ ∠4=(180°－∠C1BC)，∠A=(180°－∠A1BA)．‎ ‎∴ ∠4=∠A． …………………………………8分 ‎∴ ∠4=∠2． ‎ ‎∵ ∠5=∠6， ‎ ‎∴ ∠A‎1C1C=∠A1BC．……………………………………………………………………9分 ‎﹙3﹚△C1FB，…………10分； △A‎1C1B，△ACB．…………11分﹙写对一个不得分﹚‎ ‎25．（本小题满分12分）‎ ‎﹙1﹚①证明：分别过点M，N作 ME⊥AB，NF⊥AB，垂足分别为点E，F． ‎ A B D C M N 图 ①‎ E F ‎∵ AD∥BC，AD＝BC， ‎ ‎∴ 四边形ABCD为平行四边形． ‎ ‎∴ AB∥CD． ‎ ‎∴ ME= NF． ‎ ‎∵S△ABM＝，S△ABN＝， ‎ ‎∴ S△ABM＝ S△ABN． ……………………………………………………………………1分 ‎②相等．理由如下：分别过点D，E作DH⊥AB，EK⊥AB，垂足分别为H，K．‎ H C 图 ②‎ A B D M F E G K 则∠DHA=∠EKB=90°． ‎ ‎∵ AD∥BE， ‎ ‎∴ ∠DAH=∠EBK． ‎ ‎∵ AD＝BE， ‎ ‎∴ △DAH≌△EBK． ‎ ‎∴ DH=EK． ……………………………2分 ‎ ‎∵ CD∥AB∥EF， ‎ ‎∴S△ABM＝，S△ABG＝， ‎ ‎∴ S△ABM＝ S△ABG. …………………………………………………………………3分 ‎﹙2﹚答：存在． …………………………………………………………………………4分 解：因为抛物线的顶点坐标是C(1，4)，所以，可设抛物线的表达式为.‎ 又因为抛物线经过点A(3，0)，将其坐标代入上式，得，解得.‎ ‎∴ 该抛物线的表达式为，即． ………………………5分 ‎∴ D点坐标为（0，3）．‎ 设直线AD的表达式为，代入点A的坐标，得，解得.‎ ‎∴ 直线AD的表达式为． ‎ 过C点作CG⊥x轴，垂足为G，交AD于点H．则H点的纵坐标为． ‎ ‎∴ CH＝CG－HG＝4－2＝2． …………………………………………………………6分 设点E的横坐标为m，则点E的纵坐标为． ‎ 过E点作EF⊥x轴，垂足为F，交AD于点P，则点P的纵坐标为，EF∥CG．‎ A 图 ③-1‎ C D B O x y H P G F P E 由﹙1﹚可知：若EP＝CH，则△ADE与△ADC的面积相等． ‎ ‎①若E点在直线AD的上方﹙如图③-1﹚，‎ 则PF=，EF＝． ‎ ‎∴ EP＝EF－PF＝=． ‎ ‎∴ ． ‎ 解得，． ……………………………7分 ‎ 当时，PF=3－2＝1，EF=1+2＝3． ‎ ‎∴ E点坐标为（2，3）． ‎ 同理 当m=1时，E点坐标为（1，4），与C点重合． ………………………………8分 ‎②若E点在直线AD的下方﹙如图③－2,③－3﹚， ‎ 则． ……………………………………………9分 ‎∴．解得，． ………………………………10分 当时，E点的纵坐标为； ‎ 当时，E点的纵坐标为． ‎ ‎∴ 在抛物线上存在除点C以外的点E，使得△ADE与△ACD的面积相等，E点的坐标为E1（2，3）；；． ………………12分 ‎﹙其他解法可酌情处理﹚ ‎ A 图③－3‎ C D B O x y H P G F P E A 图③－2‎ C D B O x y H P G F P E ‎ ‎