2009年湖北省孝感市初中毕业生学业考试试题及答案 9页

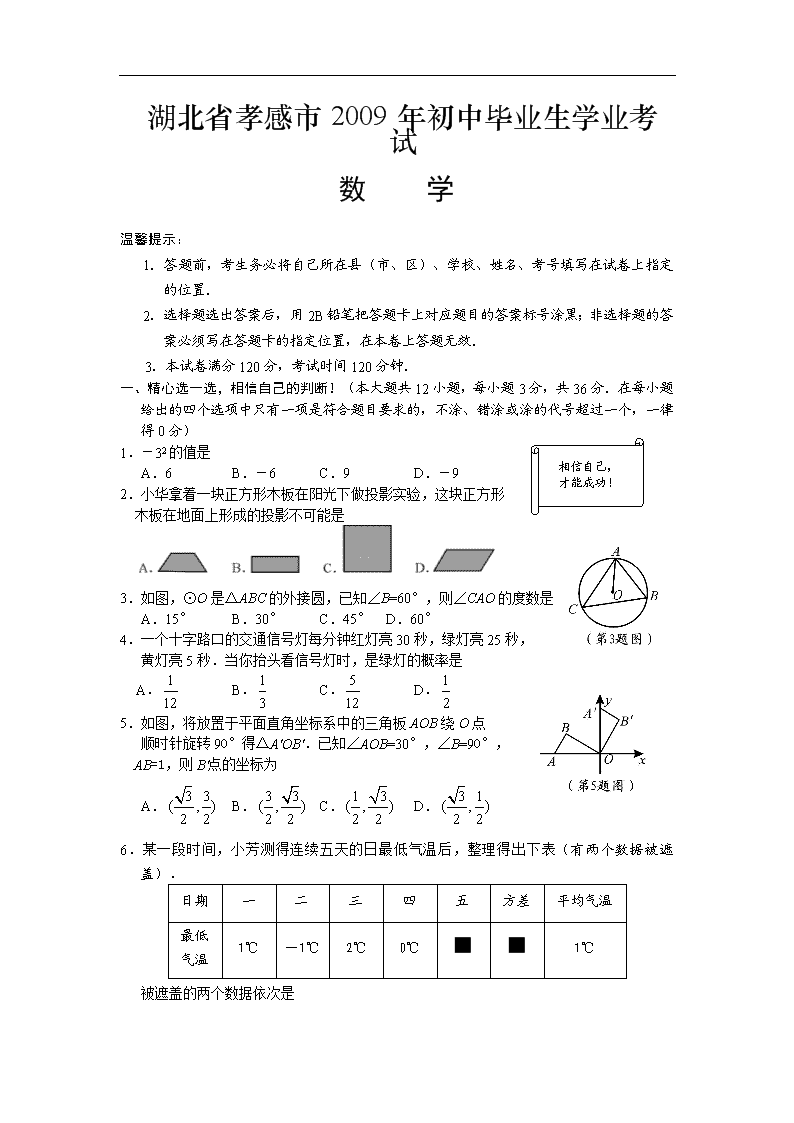
湖北省孝感市2009年初中毕业生学业考试 数 学 温馨提示：‎ ‎1．答题前，考生务必将自己所在县（市、区）、学校、姓名、考号填写在试卷上指定的位置．‎ ‎2．选择题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；非选择题的答案必须写在答题卡的指定位置，在本卷上答题无效．‎ ‎3．本试卷满分120分，考试时间120分钟．‎ 相信自己，‎ 才能成功！‎ 一、精心选一选，相信自己的判断！（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中只有一项是符合题目要求的，不涂、错涂或涂的代号超过一个，一律得0分）‎ ‎1．－32的值是 A．6 B．－‎6 ‎‎ ‎ C．9 D．－9 ‎ ‎2．小华拿着一块正方形木板在阳光下做投影实验，这块正方形 木板在地面上形成的投影不可能是 ‎3．如图，⊙O是△ABC的外接圆，已知∠B=60°，则∠CAO的度数是 A．15° B．30° C．45° D．60° ‎ ‎4．一个十字路口的交通信号灯每分钟红灯亮30秒，绿灯亮25秒，‎ 黄灯亮5秒．当你抬头看信号灯时，是绿灯的概率是 A． B． C． D．‎ ‎5．如图，将放置于平面直角坐标系中的三角板AOB绕O点 顺时针旋转90°得△A′OB′．已知∠AOB=30°，∠B=90°，‎ AB=1，则B′点的坐标为 A． B． C． D．‎ ‎6．某一段时间，小芳测得连续五天的日最低气温后，整理得出下表（有两个数据被遮盖）．‎ 日期 一 二 三 四 五 方差 平均气温 最低气温 ‎1℃‎ ‎－‎‎1℃‎ ‎2℃‎ ‎0℃‎ ‎■‎ ‎■‎ ‎1℃‎ 被遮盖的两个数据依次是 A．‎3℃‎，2 B．‎3℃‎， C．‎2℃‎，2 D．‎2℃‎，‎ ‎7．如图，正方形ABCD内有两条相交线段MN、EF，M、N、E、F分 别在边AB、CD、AD、BC上．小明认为：若MN = EF，则MN⊥EF；‎ 小亮认为: 若MN⊥EF，则MN = EF．你认为 A．仅小明对 B．仅小亮对 C．两人都对 D．两人都不对 ‎ ‎8．关于x的方程的解是正数，则a的取值范围是 A．a＞－1 B．a＞－1且a≠0 ‎ C．a＜－1 D．a＜－1且a≠－2‎ ‎9．美是一种感觉，当人体下半身长与身高的比值越接近0.618时，越给 人一种美感．如图，某女士身高‎165cm，下半身长x与身高l的比值 是0.60，为尽可能达到好的效果，她应穿的高跟鞋的高度大约为 A．‎4cm B．‎6cm C．‎8cm D．‎‎10cm ‎10．将函数的图象向右平移a个单位，得到函数 的图象，则a的值为 A．1 B．‎2 ‎C．3 D．4 ‎ ‎11．如图，把一个棱长为3的正方体的每个面等分成9个小正方 形，然后沿每个面正中心的一个正方形向里挖空（相当于挖 去了7个小正方体），所得到的几何体的表面积是 A．78 B．‎72 ‎C．54 D．48 ‎ ‎12．对于每个非零自然数n，抛物线与x轴交于An、Bn两点，以表示这两点间的距离，则的值是 A． B． C． D． ‎ 二、细心填一填，试试自己的身手！（本大题共6小题，每小题3分，共18分．请将结果直接填写在答题卡相应位置上）‎ ‎13．如图，角的顶点为O，它的一边在x轴的正半轴上，‎ 另一边OA上有一点P（3，4），则 ▲ ．‎ ‎14．关于x的不等式组的解集是，则m = ▲ ．‎ ‎15．若,且,,则 ▲ ．‎ ‎16．对于任意两个实数对（a，b）和（c，d），规定：当且仅当a＝c且b＝d时， ‎ ‎（a，b）=（c，d）．定义运算“”：（a，b）（c，d）=（ac－bd，ad＋bc）．‎ 若（1，2）（p，q）=（5，0），则p＝ ▲ ，q＝ ▲ ．‎ ‎17．如图，点M是△ABC内一点，过点M分别作直线平行于△ABC的各边，所形成的三个小三角形△1、△2、△3（图中阴影部分）的面积分别是4，9和49．则△ABC的面积是 ▲ ．‎ ‎18．在平面直角坐标系中，有A（3，－2），B（4，2）两点，现另取一点C（1，n），‎ 当n = ▲ 时，AC + BC的值最小．‎ 三、用心做一做，显显自己的能力！（本大题共7小题，满分66分．解答写在答题卡上）‎ 细心读题，认真解答！‎ ‎19．（本题满分6分） ‎ 已知：，，求下列各式的值.‎ ‎（1）；（3分） （2）．（3分）‎ ‎20．（本题满分8分）‎ 三个牧童A、B、C在一块正方形的牧场上看守一群牛，为保证公平合理，他们商量将牧场划分为三块分别看守，划分的原则是：①每个人看守的牧场面积相等；②在每个区域内，各选定一个看守点，并保证在有情况时他们所需走的最大距离（看守点到本区域内最远处的距离）相等．按照这一原则，他们先设计了一种如图1的划分方案：把正方形牧场分成三块相等的矩形，大家分头守在这三个矩形的中心（对角线交点），看守自己的一块牧场．‎ 过了一段时间，牧童B和牧童C又分别提出了新的划分方案．‎ 牧童B的划分方案如图2：三块矩形的面积相等，牧童的位置在三个小矩形的中心．‎ 牧童C的划分方案如图3：把正方形的牧场分成三块矩形，牧童的位置在三个小矩形的中心，并保证在有情况时三个人所需走的最大距离相等．‎ 请回答：‎ ‎（1）牧童B 的划分方案中，牧童 ▲ （填A、B或C）在有情况时所需走的最大距离较远；（3分）‎ ‎（2）牧童C的划分方案是否符合他们商量的划分原则？为什么？（提示：在计算时可取正方形边长为2）（5分）‎ ‎21．（本题满分10分）‎ 某班6名同学组成了一个“帮助他人，快乐自己”‎ 的体验小组．他们约定一学期每人至少参加一次公益活 动．学期结束后，他们参加公益活动的统计图如右．‎ ‎（1）这个体验小组一学期参加公益活动的人均次数 是 ▲ 次；（4分）‎ ‎（2）从这6名同学中任选两名同学（不考虑先后顺序），他们参加公益活动的次数恰好相等的概率是多少？（6分）‎ ‎22．（本题满分10分）‎ 如图，⊙O是Rt的外接圆，，点P是圆外一点，PA切⊙O于点A，且PA = PB．‎ ‎（1）求证：PB是⊙O的切线；（5分）‎ ‎（2）已知，，求⊙O的半径．（5分）‎ ‎23．（本题满分10分）‎ 已知抛物线（k为常数，且k＞0）．‎ ‎（1）证明：此抛物线与x轴总有两个交点；（4分）‎ ‎（2）设抛物线与x轴交于M、N两点，若这两点到原点的距离分别为OM、ON，且，求k的值．（6分）‎ ‎24．（本题满分10分） ‎ ‎5月份，某品牌衬衣正式上市销售．‎5月1日的销售量为10件，‎5月2日的销售量为35件，以后每天的销售量比前一天多25件，直到日销售量达到最大后，销售量开始逐日下降，至此，每天的销售量比前一天少15件，直到‎5月31日销售量为0．设该品牌衬衣的日销量为p（件），销售日期为n（日），p与n之间的关系如图所示．‎ ‎（1）写出p关于n的函数关系式p = ▲ （注明n的取值范围）；（3分）‎ ‎（2）经研究表明，该品牌衬衣的日销量超过 ‎150件的时间为该品牌衬衣的流行期．请问：该品牌衬衣本月在市面的流行期是多少天？（4分）‎ ‎（3）该品牌衬衣本月共销售了 ▲ 件．（3分）‎ ‎25．（本题满分12分）‎ 如图，点P是双曲线上一动点，过点P作x轴、y轴的垂线，分别交x轴、y轴于A、B两点，交双曲线y= （0＜k2＜|k1|）于E、F两点．‎ ‎（1）图1中，四边形PEOF的面积S1= ▲ (用含k1、k2的式子表示)；（3分）‎ ‎（2）图2中，设P点坐标为（－4，3）．‎ ‎①判断EF与AB的位置关系，并证明你的结论；（4分）‎ ‎②记，S2是否有最小值？若有，求出其最小值；若没有，请说明理由．（5分）‎ 做完试卷，‎ 认真检查！‎ 数学参考答案及评分说明 一、选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 D A B C A A C D C B B D 二、填空题 ‎13．(或0.8); 14．–3; 15．49或1; ‎ ‎16．1，–2; 17．144; 18．(或–0.4)‎ 说明：第15题只答对一解给2分；第16题只填对一空给2分．‎ 三、解答题 ‎19．解：（1）原式＝ ……………………………………… 1分 ‎＝ ＝＝ 12 ……………………… 3分 ‎ ‎（2）原式＝ ………………………………………4分 ‎＝ ＝＝ …… 6分 说明：以上两小题，将x、y的值直接代入求值，只要正确即可得分.‎ ‎20．（1） C ； …………………………………………3分 ‎ （2）牧童C的划分方案不符合他们商量的划分原则． ………………… 4分 理由如下：如图，在正方形DEFG中，四边形HENM、MNFP、DHPG都是矩形，且HN=NP=HG．可知EN=NF，S矩形HENM＝ S矩形MNFP． ……………………… 5分 取正方形边长为2，设HD=x，则HE=2－x.‎ 在Rt△HEN和Rt△DHG中，‎ 由HN=HG得：EH2+EN2=DH2+DG2 ，‎ 即：．‎ 解得，．∴． ……………… 7分 ‎ ∴S矩形HENM = S矩形MNFP =，S矩形DHPG =．∴S矩形HENM ≠ S矩形DHPG．‎ ‎∴牧童C的划分方案不符合他们商量的划分原则． ……………………… 8分 ‎21．解：（1）3； …………………………………………… 4分 ‎（2）设这6名同学中只参加1次公益活动的是A，参加了三次公益活动的 是B1、B2、B3，参加了四次公益活动的是C1、C2．‎ 从中任选两名同学，有AB1、AB2、AB3、AC1、AC2、B1B2、B1B3、B‎1C1、B‎1C2、‎ B2B3、B‎2C1、B‎2C2、B‎3C1、B‎3C2、C‎1C2共15种情况． …………… 6分 参加公益活动次数相等的有B1B2、B1B3、B2B3、C‎1C2共4种情况．………8分 ‎∴所求概率． …………………………………… 10分 说明：求概率时利用列表法或画树形图法亦可．‎ ‎22.（1）证明：连接OB．‎ ‎∵OA=OB，∴∠OAB=∠OBA．‎ ‎∵PA=PB，∴∠PAB=∠PBA．‎ ‎∴∠OAB+∠PAB=∠OBA+∠PBA，‎ 即∠PAO=∠PBO …………………2分 又∵PA是⊙O的切线，∴∠PAO=90°，‎ ‎∴∠PBO=90°，∴OB⊥PB ． …………………………………………4分 又∵OB是⊙O半径，‎ ‎∴PB是⊙O的切线． …………………………………………5分 说明：还可连接OB、OP，利用△OAP≌△OBP来证明OB⊥PB．‎ ‎（2）解：连接OP，交AB于点D．‎ ‎∵PA=PB，∴点P在线段AB的垂直平分线上．‎ ‎∵OA=OB，∴点O在线段AB的垂直平分线上．‎ ‎∴OP垂直平分线段AB． …………………………………7分 ‎∴∠PAO=∠PDA =90°．‎ 又∵∠APO=∠DPA，∴△APO∽△DPA．‎ ‎∴，∴AP2 = PO·DP．‎ 又∵OD =BC =，∴PO（PO–OD）=AP2．‎ 即：PO2–PO=，解得 PO=2． ………………9分 在Rt△APO中，，即⊙O的半径为1． …………10分 说明：求半径时，还可证明△PAO∽△ABC或在Rt△OAP中利用勾股定理．‎ ‎23.（1）证明：△=． ………………2分 ‎∵k >0，∴△= 4k2 >0 ． ……………………………3分 ‎∴此抛物线与x轴总有两个交点． ………………4分 ‎（2）解：方程的解为． ……………6分 ‎∵，∴OM > ON．∵k > 0，∴M ，N ‎ ‎∴OM=，ON=． ……………………8分 ‎∴，解得，k=2． ………………………10分 说明：第（2）题还可利用根与系数的关系来解答．‎ ‎24. 解：（1）； ……………3分 ‎（2）由题意，有：‎ ‎ …………………………………… 5分 解得， ，整数n的值可取7，8，9，……20共14个．‎ ‎∴该品牌衬衣本月在市面的流行期为14天． …………………7分 ‎（3）4335件． … ……………………………… 10分 ‎25．解：（1）； … ………………………………3分 ‎（2）①EF∥AB． ……………………………………4分 证明：如图，由题意可得A（–4，0），B（0，3），， ．‎ ‎∴PA=3，PE=，PB=4，PF=．‎ ‎∴，‎ ‎∴． ………………………… 6分 ‎ 又∵∠APB=∠EPF．‎ ‎∴△APB ∽△EPF，∴∠PAB=∠PEF．‎ ‎∴EF∥AB． …………………………… 7分 ‎②S2没有最小值，理由如下：‎ 过E作EM⊥y轴于点M，过F作FN⊥x轴于点N，两线交于点Q．‎ 由上知M（0，），N（，0），Q（，）． ……………… 8分 而S△EFQ= S△PEF，‎ ‎∴S2＝S△PEF－S△OEF＝S△EFQ－S△OEF＝S△EOM＋S△FON＋S矩形OMQN ‎＝‎ ‎＝‎ ‎=． ………………………… 10分 当时，S2的值随k2的增大而增大，而0＜k2＜12． …………… 11分 ‎∴0＜S2＜24，s2没有最小值． …………………………… 12分 说明：1．证明AB∥EF时，还可利用以下三种方法．方法一：分别求出经过A、B两点和经过E、F两点的直线解析式，利用这两个解析式中x的系数相等来证明AB∥EF；方法二：利用＝来证明AB∥EF；方法三：连接AF、BE，利用S△AEF＝S△BFE得到点A、点B到直线EF的距离相等，再由A、B两点在直线EF同侧可得到AB∥EF．‎ ‎2．求S2的值时，还可进行如下变形：‎ S2＝ S△PEF－S△OEF＝S△PEF－（S四边形PEOF－S△PEF）＝2 S△PEF－S四边形PEOF，再利用第（1）题中的结论．‎ 注意：1．按照评分标准分步评分，不得随意变更给分点；‎ ‎2．第19题至第25题的其它解法，只要思路清晰，解法正确，都应按步骤给予相应分数．‎