中考数学专题复习模拟演练图形的平移轴对称旋转 8页

中考专题复习模拟演练:图形的平移、轴对称、旋转 一、选择题 ‎1.在平面直角坐标系中，点（2，﹣1）关于原点对称的点的坐标是（　　） ‎ A. （2，1）                   B. （﹣2，1）                      C. （﹣1，2）                         D. （﹣2，﹣1）‎ ‎2.在图示的四个汽车标志图案中，能用平移变换来分析其形成过程的图案是（   ） ‎ A. B. C. D.‎ ‎3.如图，8×8方格纸的两条对称轴EF，MN相交于点O，图a到图b的变换是（　　） ​ ‎ A. 绕点O旋转180° B. 先向上平移3格，再向右平移4格 C. 先以直线MN为对称轴作轴对称，再向上平移4格 D. 先向右平移4格，再以直线EF为对称轴作轴对称 ‎4.将点A（2，1）向左平移2个单位长度得到点A′，则点A′的坐标是（  ） ‎ A. (2，3)                           B. （0，1）                           C. （4，1）                           D. （2，－１）‎ ‎5.如图，若△ABC中任意一点P（x0 ， y0）经平移后对应点为P1（x0+5，y0－3）那么将△ABC作同榉的平移得到△A1B1C1 ， 则点A的对应点A1的坐标是（　） ‎ A. （4，1）　                      B. （9，一4）                      C. （一6，7）                      D. （一1，2）‎ ‎6.下列“表情图”中，属于轴对称图形的是（   ） ‎ A.                                       B.                                       C.                                       D. 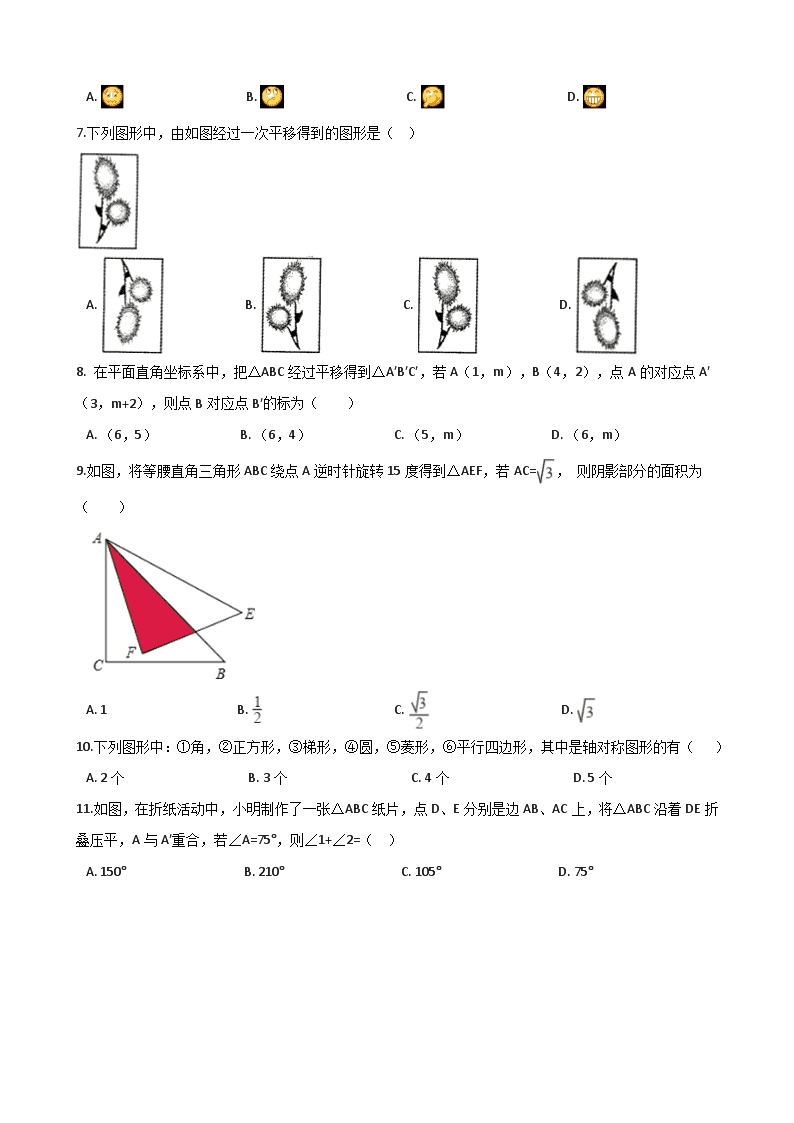‎ ‎7.下列图形中，由如图经过一次平移得到的图形是（   ） ‎ A.                          B.                          C.                          D. ‎ ‎8. 在平面直角坐标系中，把△ABC经过平移得到△A′B′C′，若A（1，m），B（4，2），点A的对应点A′（3，m+2），则点B对应点B′的标为（　　） ‎ A. （6，5）                          B. （6，4）                          C. （5，m）                          D. （6，m）‎ ‎9.如图，将等腰直角三角形ABC绕点A逆时针旋转15度得到△AEF，若AC=， 则阴影部分的面积为（　　） ‎ A. 1                                         B.                                          C.                                          D. ‎ ‎10.下列图形中：①角，②正方形，③梯形，④圆，⑤菱形，⑥平行四边形，其中是轴对称图形的有（     ） ‎ A. 2个                                       B. 3个                                       C. 4个                                       D. 5个 ‎11.如图，在折纸活动中，小明制作了一张△ABC纸片，点D、E分别是边AB、AC上，将△ABC沿着DE折叠压平，A与A′重合，若∠A=75°，则∠1+∠2=（   ） ‎ A. 150°                                     B. 210°                                     C. 105°                                     D. 75°‎ ‎12.如图，在等边三角形ABC中，BC边上的高AD=6，E是高AD上的一个动点，F是边AB的中点，在点E运动的过程中，存在EB+EF的最小值，则这个最小值是(    ) ‎ A. 3                                           B. 4                                           C. 5                                           D. 6‎ 二、填空题 ‎ ‎13.点P（﹣2，3）关于x轴的对称点的坐标是________． ‎ ‎14. 已知点P（3，a）关于y轴的对称点为Q（b，2），则ab=​ ________. ‎ ‎15.如图，正方形ABCD边长为2，E为CD的中点，以点A为中心，把△ADE顺时针旋转90°得△ABF，连接EF，则EF的长等于________． ‎ ‎16.如图所示，M的坐标是________ ，与M点关于直线m成轴对称的点坐标是________ ． ‎ ‎17.如图，将边长为6cm的正方形ABCD折叠，使点D落在AB边的中点E处，折痕为FH，点C落在Q处，EQ与BC交于点G，则△EBG的周长是________ cm． ‎ ‎18.把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G、D、C分别在M、N的位置上，若∠EFG=55°，则∠1=________°，∠2=________°．‎ ‎19.如图，点O是AC的中点，将周长为4cm的菱形ABCD沿对角线AC方向平移AO长度得到菱形OB′C′D′，则四边形OECF的周长是________ cm．  ‎ ‎20.一条船由原点O出发航行，先向东航行10千米到A点，接着又向北航行20千米至B点，最后又向东航行15千米至C点，则C点的坐标为________。 ‎ 三、解答题 ‎ ‎21.如图,将矩形沿EF折叠,使B1点落在边上的B点处;再将矩形沿BG折叠,使D1点落在D点处且BD过F点． （1）求证:四边形BEFG是平行四边形; （2）当是多少度时,四边形BEFG为菱形?试说明理由． ‎ ‎22.△ABC和△ECD都是等边三角形 （1）如图1，若B、C、D三点在一条直线上，求证：BE=AD； （2）保持△ABC不动，将△ECD绕点C顺时针旋转，使∠ACE=90°（如图2），BC与DE有怎样的位置关系？说明理由． ‎ ‎23.如图，在平面直角坐标系中，点A，B的坐标分别为（﹣1，0），（3，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD． （1）求点C，D的坐标及四边形ABDC的面积S四边形ABDC； （2）在y轴上是否存在一点P，连接PA，PB，使S△PAB=S四边形ABDC？若存在这样一点，求出点P的坐标；若不存在，试说明理由； ‎ ‎24.已知∠AOB＝90°，在∠AOB的平分线OM上有一点C，将一个三角板的直角顶点与C重合，它的两条直角边分别与OA，OB(或它们的反向延长线)相交于点D，E. 当三角板绕点C旋转到CD与OA垂直时(如图①)，易证：OD＋OE＝ OC； 当三角板绕点C旋转到CD与OA不垂直时，即在图②，图③这两种情况下，上述结论是否仍然成立？若成立，请给予证明；若不成立，线段OD，OE，OC之间又有怎样的数量关系？请写出你的猜想，不需证明．    ‎ 参考答案 ‎ 一、选择题 ‎ B D D B A D C B C C A D ‎ 二、填空题 ‎13. （﹣2，﹣3） ‎ ‎14. -6 ‎ ‎15. ‎ ‎16. （3，3）；（﹣7，3） ‎ ‎17. 12 ‎ ‎18. 70；110 ‎ ‎19. 2 ‎ ‎20. （25,20） ‎ 三、解答题 ‎21. 解;（1）∵A1D1∥B1C1, ∴∠B1FE=∠FEB． 又∵∠B1FE=∠BFE, ∴∠FEB=∠BFE． ∴BE=BF． 同理可得：FG=BF． ∴BE=FG, 又∵BE∥FG, ∴四边形BEFG是平行四边形; （2）当∠B1FE=60°时,四边形EFGB为菱形． 理由如下： ∵∠B1FE=60°, ∴∠BFE=∠BEF=60°, ∴△BEF为等边三角形,即BE=EF． ∵四边形BEFG是平行四边形,BE=EF． ∴四边形BEFG是菱形（一组邻边相等的平行四边形是菱形）． ‎ ‎22. 解：（1）∵△ABC和△ECD都是等边三角形，∴AC=BC，EC=DC，∠ACB=∠ECD=60°. ∴∠ACB+∠ACE=∠ECD+∠ACE，即∠ACD=∠BCE. ∴△ACD≌△BCE. ∴AD=BE. （2）BC垂直平分DE，理由如下： 如图， 延长BC交DE于M， ∵∠ACB=60°，∠ACE=90°，∴∠ECM=180°-∠ACB-∠ACE=30°. ∵∠DCM=∠ECD-∠ECM=30°，∴∠ECM=∠DCM. ∵△ECD是等边三角形，∴CM垂直平分DE，即BC垂直平分DE． ‎ ‎23. 解：（1）依题意，得C（0，2），D（4，2）， ∴S四边形ABDC=AB×OC=4×2=8； （2）存在． 设点P到AB的距离为h， S△PAB=×AB×h=2h， 由S△PAB=S四边形ABDC ， 得2h=8，解得h=4， ∴P（0，4）或（0，﹣4）； ‎ ‎24. 证明：过点C分别作OA，OB的垂线，垂足分别为P，Q. 有△CPD≌△CQE， ∴DP＝EQ， ∵OP＝OD＋DP，OQ＝OE－EQ， 又∵OP＋OQ＝ OC， 即OD＋DP＋OE－EQ＝ OC， ∴OD＋OE＝ OC. 图③不成立， 有数量关系：OE－OD＝ OC 过点C分别作CK⊥OA， CH⊥OB， ∵OC为∠AOB的角平分线，且CK⊥OA，CH⊥OB， ∴CK=CH，∠CKD=∠CHE=90°， 又∵∠KCD与∠HCE都为旋转角， ∴∠KCD=∠HCE， ∴△CKD≌△CHE， ∴DK=EH， ∴OE-OD=OH+EH-OD=OH+DK-OD=OH+OK， 由（1）知：OH+OK= OC， ∴OD，OE，OC满足OE-OD= OC． ‎