2020中考数学复习 第20课时 三角形与全等三角形（无答案） 3页

第20课时 三角形与全等三角形 ‎【课前展练】‎ ‎1．如图，在△ABC中，AB=AC=5，BC=6，点M为BC中点，MN⊥AC于点N，则MN的长是___________‎ A B C D ‎2．如图，将三角尺的直角顶点放在直尺的一边上，∠1=，∠2=，则∠3= ．‎ C B A M N ‎3．如图，已知那么添加下列一个条件后，仍无法判定的是（ ） ‎ ‎ A．　　B． C． D．‎ ‎4．一个三角形的两边长分别为3和7，且第三边长为整数，这样的三角形的周长最小值是 ( )‎ A．14 B．‎15 ‎ C．16 D．17‎ ‎5．若等腰三角形一腰上的高和另一腰的夹角为25°，则该三角形的一个底角为（　　）‎ A．32.5° B．57.5° C．65°或57.5° D．32.5°或57.5°‎ ‎6．如图，在等腰梯形ABCD中，AB＝DC，AC、BD交于点O，‎ 则图中全等三角形共有（ ）‎ A．2对 B．3对 C．4对 D．5对 ‎【考点梳理】‎ 考点一、三角形的分类：‎ ‎1．三角形按角分为______________，______________，_____________．‎ ‎2．三角形按边分为_______________,__________________.‎ 考点二、三角形的性质：‎ ‎1．三角形中任意两边之和____第三边，两边之差_____第三边 ‎2．三角形的内角和为_______，外角与内角的关系：__________________．‎ 考点三、三角形中的主要线段：‎ 三角形的中线、高线、角平分线都是____________．(线段、射线、直线)‎ 考点四、全等三角形 ‎1. 全等三角形的性质：全等三角形___________，____________.‎ 3‎ ‎2. 三角形全等的判定方法有:_______、______、_______、______.直角三角形全等的判定除以上的方法还有________.‎ ‎3. 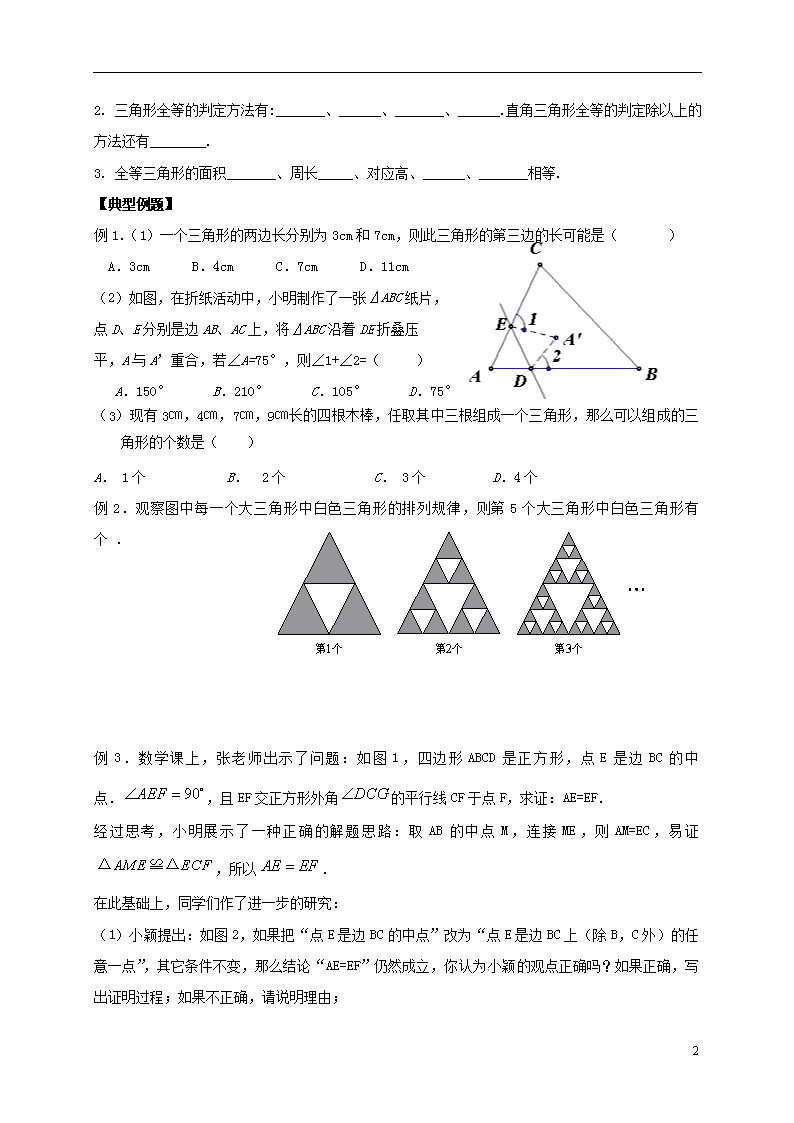全等三角形的面积_______、周长_____、对应高、______、_______相等.‎ ‎【典型例题】‎ 例1．（1）一个三角形的两边长分别为‎3cm和‎7cm，则此三角形的第三边的长可能是（ ）‎ A．‎3cm B．‎4cm C．‎7cm D．‎‎11cm ‎（2）如图，在折纸活动中，小明制作了一张⊿ABC纸片，‎ 点D、E分别是边AB、AC上，将⊿ABC沿着DE折叠压 平，A与A’重合，若∠A=75°，则∠1+∠2=（ ）‎ A．150° B．210° C．105° D．75°‎ ‎（3）现有3㎝，4㎝，7㎝，9㎝长的四根木棒，任取其中三根组成一个三角形，那么可以组成的三角形的个数是（ 　）‎ A． 1个 B． 2个 C． 3个 D．4个 例2．观察图中每一个大三角形中白色三角形的排列规律，则第5个大三角形中白色三角形有 个 ．‎ 例3．数学课上，张老师出示了问题：如图1，四边形ABCD是正方形，点E是边BC的中点．，且EF交正方形外角的平行线CF于点F，求证：AE=EF．‎ 经过思考，小明展示了一种正确的解题思路：取AB的中点M，连接ME，则AM=EC，易证，所以．‎ 在此基础上，同学们作了进一步的研究：‎ ‎（1）小颖提出：如图2，如果把“点E是边BC的中点”改为“点E是边BC上（除B，C外）的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；‎ 3‎ ‎（2）小华提出：如图3，点E是BC的延长线上（除C点外）的任意一点，其他条件不变，结论“AE=EF”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说A D F C G E B 图1‎ A D F C G E B 图2‎ A D F C G E B 图3‎ 明理由．‎ 3‎