2011年福建省龙岩中考数学试题及答案 9页

‎2011年龙岩市初中毕业、升学考试 数学试题 ‎ ‎(满分：150分考试时间：l20分钟)‎ 注意：‎ ‎ 请把所有答案填涂或书写到答题卡上!请不要错位、越界答题！‎ ‎ 在本试题上答题无效。‎ 提示：抛物线的对称轴，顶点坐标是 ()‎ 一、选择题(本大题共l0题．每题4分．共40分。每题的四个选项中．只有一个符合题意，‎ ‎ 请将正确的选项填涂到答题卡上)‎ ‎1．5的相反数是 A． B. 5 C. D. ‎ ‎2．下列运算正确的是 ‎ A． B． C． D．‎ ‎3．下列图形中是中心对称图形的是 ‎4．的计算结果是 A． B． C． D．‎ ‎5．如图，该几何体的主视图是 ‎6．如图．若乙、丙都在甲的北偏东70°方向上．乙在丁的正北方向上，且乙到丙、丁的距离相同．则α的度数是 ‎ A．25° B．30° C．35° D．40°‎ ‎7．数名射击运动员第一轮比赛成绩如下表所示；‎ 环数 ‎7‎ ‎8‎ ‎9‎ ‎10‎ 人数 ‎4‎ ‎2‎ ‎3‎ ‎1‎ 则他们本轮比赛的平均成绩是 A．7.8环 B．7.9环 C. 8.l环 D．8.2环 ‎8．右图可以折叠成的几何体是 A．三棱柱 B．四棱柱 C．圆柱 D．圆锥 ‎9．下列图象中，能反映函数y随x增大而减小的是 ‎10．现定义运算“★”，对于任意实数a、b，都有a★b=，如：3★5=，若x★2=6，则实数x的值是 A．或 B．4或 C．4或 D．或2‎ 二、填空题（本大题共7题，每题3分，共21 分。请将答案填入答题卡相应位置）‎ ‎11．一组数据10，14，20，24．19，1 6的极差是____________。‎ ‎12．若式子有意义，则实数的取值范围是____________。‎ ‎13．据第六次全国人口普查统计，我国人口总数约有l 370 000 000人，用科学记数法表示为___________人。‎ ‎14．袋子中有3个红球和6个白球，这些球除颇色外均完全相同，则从袋子中随机摸出一个球是白球的概率是_________，‎ ‎15. 如图，菱形ABCD周长为8㎝．∠BAD=60°，则AC=___________cm。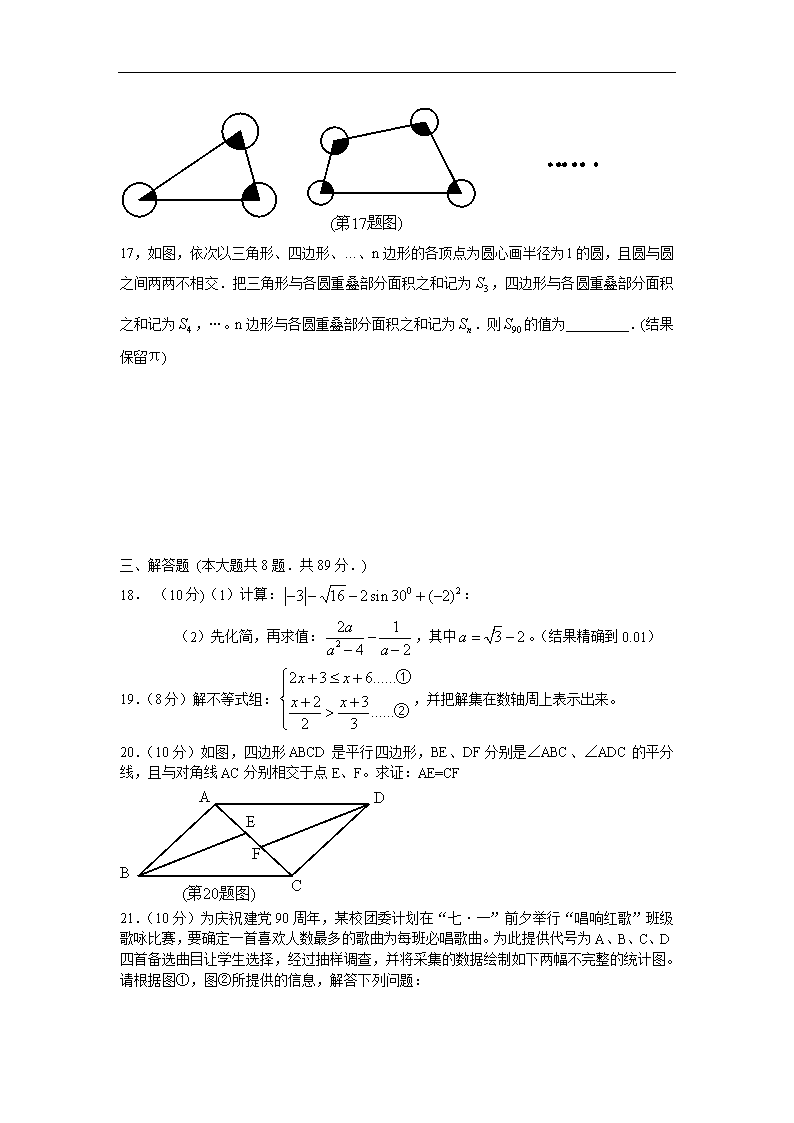‎ ‎16．如图．⊙O是△ABC的外接圆AC是⊙O的直径，OD⊥BC于点D．OD=2．则AB的长是_________‎ ‎17，如图，依次以三角形、四边形、…、n边形的各顶点为圆心画半径为l的圆，且圆与圆之间两两不相交．把三角形与各圆重叠部分面积之和记为，四边形与各圆重叠部分面积之和记为，…。n边形与各圆重叠部分面积之和记为．则的值为_________．(结果保留π) ‎ 三、解答题 (本大题共8题．共89分．)‎ ‎18． （10分)（1）计算：：‎ ‎ （2）先化简，再求值：，其中。（结果精确到0.01）‎ ‎19．（8分）解不等式组：，并把解集在数轴周上表示出来。‎ ‎20．（10分）如图，四边形ABCD是平行四边形，BE、DF分别是∠ABC、∠ADC的平分线，且与对角线AC分别相交于点E、F。求证：AE=CF ‎21．（10分）为庆祝建党90周年，某校团委计划在“七·一”前夕举行“唱响红歌”班级歌咏比赛，要确定一首喜欢人数最多的歌曲为每班必唱歌曲。为此提供代号为A、B、C、D四首备选曲目让学生选择，经过抽样调查，并将采集的数据绘制如下两幅不完整的统计图。请根据图①，图②所提供的信息，解答下列问题：‎ ‎（1）本次抽样调查的学生有_________名，其中选择曲目代号为A的学生占抽样总数的百分比是________%；‎ ‎（2）请将图②补充完整；‎ ‎（3）若该校共有1200名学生，根据抽样调查的结果估计全校共有多少名学生选择此必唱歌曲？（要有解答过程）‎ ‎22. （12分）一副直角三角板叠放如图所示，现将含45°角的三角板ADE固定不动，把含30°角的三角板ABC绕顶点A顺时针旋转∠α（α=∠BAD且0°<α<180°），使两块三角板至少有一组边平行。‎ ‎（1）如图①，α=______°时，BC∥DE；‎ ‎（2）请你分别在图②、图③的指定框内，各画一种符合要求的图形，标出α，并完成各项填空：‎ 图②中α=______°时，______∥______；图③中α=______°时，______∥______。‎ ‎23. (12分)‎ ‎ 周六上午8：O0小明从家出发，乘车1小时到郊外某基地参加社会实践活动，在基地活动2.2小时后，因家里有急事，他立即按原路以4千米/时的平均速度步行返回．同时爸爸开车从家出发沿同一路线接他，在离家28千米处与小明相遇。接到小明后保持车速不变，立即按原路返回．设小明离开家的时间为x小时，小名离家的路程y (干米) 与x (小时)之间的函致图象如图所示，‎ ‎(1)小明去基地乘车的平均速度是________千米/小时，爸爸开车的平均速度应是________千米/小时；‎ ‎(2)求线段CD所表示的函敛关系式；‎ ‎(3)问小明能否在12：0 0前回到家？若能，请说明理由：若不能，请算出12：00时他离家的路程，‎ ‎24．(13分)如图，已知抛物线与x轴相交于A、B两点，其对称轴为直线，且与x轴交于点D，AO=1．‎ ‎(1) 填空：b=_______。c=_______，‎ ‎ 点B的坐标为(_______，_______)：‎ ‎(2) 若线段BC的垂直平分线EF交BC于点E，交x轴于点F．求FC的长；‎ ‎(3) 探究：在抛物线的对称轴上是否存在点P，使⊙P与x轴、直线BC都相切？若存在，请求出点P的坐标；若不存在，请说明理由。‎ ‎25. (14分)如图，在直角梯形ABCD中，∠D=∠BCD=90°，∠B=60°， AB=6，AD=9，‎ 点E是CD上的一个动点(E不与D重合)，过点E作EF∥AC，交AD于点F(当E运 动到C时，EF与AC重合巫台)．把△DEF沿EF对折，点D的对应点是点G，设DE=x，‎ ‎ △GEF与梯形ABCD重叠部分的面积为y。‎ ‎(1) 求CD的长及∠1的度数；‎ ‎(2) 若点G恰好在BC上，求此时x的值；‎ ‎(3) 求y与x之间的函数关系式。并求x为何值时，y的值最大?最大值是多少?‎ 龙岩2011年中考数学简要答案（自己做的，有错自行修改）‎ 一、 选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 C B D A B C C A D B 二、 填空题 ‎11、14 12、 13、 14、 15、 16、4 17、44π ‎ 三、 解答题 ‎18、（1）解：原式=2 （2）原式化简=，当时，原式=‎ ‎19、解：由①得，，由②得，∴，画图略。‎ ‎20、证明略 ‎21、（1）180，20（2）选C的有72人，如图 ‎（3）1200×=480（名）‎ ‎22、（1）15‎ ‎（2）图②中α=60°时，BC∥DA，图③中α=105°时，BC∥EA ‎23、（1）30，56 （20线段CD的表达式：‎ ‎（3）不能。小明从家出发到回家一共需要时间：1+2.2+2÷4×2=4.2（小时），从8:00经过4.2小时已经过了12:00，‎ ‎∴不能再12:00前回家，此时离家的距离：56×0.2=11.2（千米）‎ ‎24、（1），B(5，0)‎ ‎（2）由（1）求得 ‎∴C（2，4）‎ ‎∵E为BC的中点，由中点坐标公式求得E的坐标为（3.5，2）‎ 易求直线BC的表达式为，整理得 设直线EF的表达式为 ‎∵EF为BC的中垂线 ‎∴EF⊥BC ‎∴‎ 把E（3.5，2）代入求得 ‎∴直线EF的表达式为，‎ 在中，令y=0，得 ‎∴F(，0)‎ ‎∴FC=FB=‎ ‎（3）存在，作∠OBC的平分线交DC于点P，则P满足条件。当然也可以作∠OBC的邻补角的平分线交DC于点P’，也满足条件，坐标求法一样。‎ 设P（2，a），则P到x轴的距离等于P到直线BC的距离。（用到点到直线的距离公式）‎ ‎∴‎ ‎∴‎ ‎∴或 解得或 ‎∴P（2，）或P（2，）。‎ ‎25、（1）CD= ∠1=30°‎ ‎（2）若点G恰好在BC上，‎ 则有GE=DE=x，EC=‎ ‎∵∠1=30°，∴∠FED=60°‎ ‎∴∠GEF=60°‎ ‎∴∠GEC=60°‎ ‎∴GE=2CE ‎∴‎ ‎∴‎ ‎（3）∵△EFG≌△EFD ‎（1）当时，随着x的增大，面积增大，此时△的面积就是重叠的面积，当时，达到最大值，为。‎ ‎（2）当，△EFG就有一部分在梯形外，如图3，‎ ‎∵GE=DE=x，EC=‎ 易求，∴‎ ‎∴NG=‎ ‎∴‎ 此时 ‎=‎ 当时，‎ 综上所述。当时，。‎