2018江西中考数学卷含答案 28页

江西省 2018 年中等学校招生考试 数 学 试 题 (满分 120, 考试时间 120 分钟) 一.选择题(每小题 3 分, 共 18 分, 在每小题只有一个正确选项) 1. －2 的约对值是( ) A. －2 B. 2 C. － 2 1 D. 2 1 2. 计算 2 2)( a ba  的结果为( ) A. b B. －b C. ab D. a b 3. 如图所示的几何体的左视图为( ) 4. 某班组织了针对 全班同学关于 “你最喜欢的一项体育活动”的问卷调 查后, 绘制出频数分布走方图, 由图可知, 下列结论正确的是( ) A. 最喜欢篮球的数最多 B. 最喜欢羽毛球的人数是最喜欢乒乓球人数的两倍 C. 全班共有 50 名学生 D. 最喜欢田径的人数点总人数的 10%. 5. 小军同学在网格纸上将某些地图进行平移操作, 他发现平移前后的两个 图形所组成所图形可以是轴对称图形. 如图所示, 现在他将正方形 ABCD 从当前位置形开始进行一次平移操作, 平移后的正方形的顶点也在格点 上, 则使平移前后的两个正方形组成轴对称图形的平移方向有( ) A. 3 B. 4 C. 5 D.无数个 6. 在平面直角坐标系中, 分别过点 A(m, 0), B(m+2, 0)作 x 轴的垂线 l1 和 l2, 探究直线 l1, 直线 l2 与双曲线 y= x 3 的关系, 下列结论中错误的是( ) A. 两直线中总有一条与双曲线相交 B. 当 m=1 时, 两直线与双曲线的交点到原点的距离相等 C. 当－2 < m < 0 时, 两直线与双曲线的交点在 y 轴两侧 D. 当两直线与双曲线都有交点时, 这两交点的最距离是 2.. 二. 填空题(每小题 3 分, 共 18 分) 7. 若分式 1 1 x 有意义, 则 x 的取值范围为________ . 8. 2018 年 5 月 13 日, 中国首艘航空母舰首次执行海上试航任务, 其排水量 超过 6 万吨, 将数 60 000 用科学记数法表示应为___________ . 9. 中国的《九章算术》是世界现代数学的两大源泉之一, 其中有一个问题: “今有牛五, 羊二, 直金十 两.牛二, 羊五, 直金八两. 问牛羊各直金几何?”译文: 今有牛 5 头, 羊 2 头, 共值金 10 两; 牛 2 头, 羊 5 头, 共值金 8 两. 问牛, 羊每头各值金多少? 设牛, 羊每头各值金 x 两, y 两. 依题意, 可列出方 程组为_______________ . 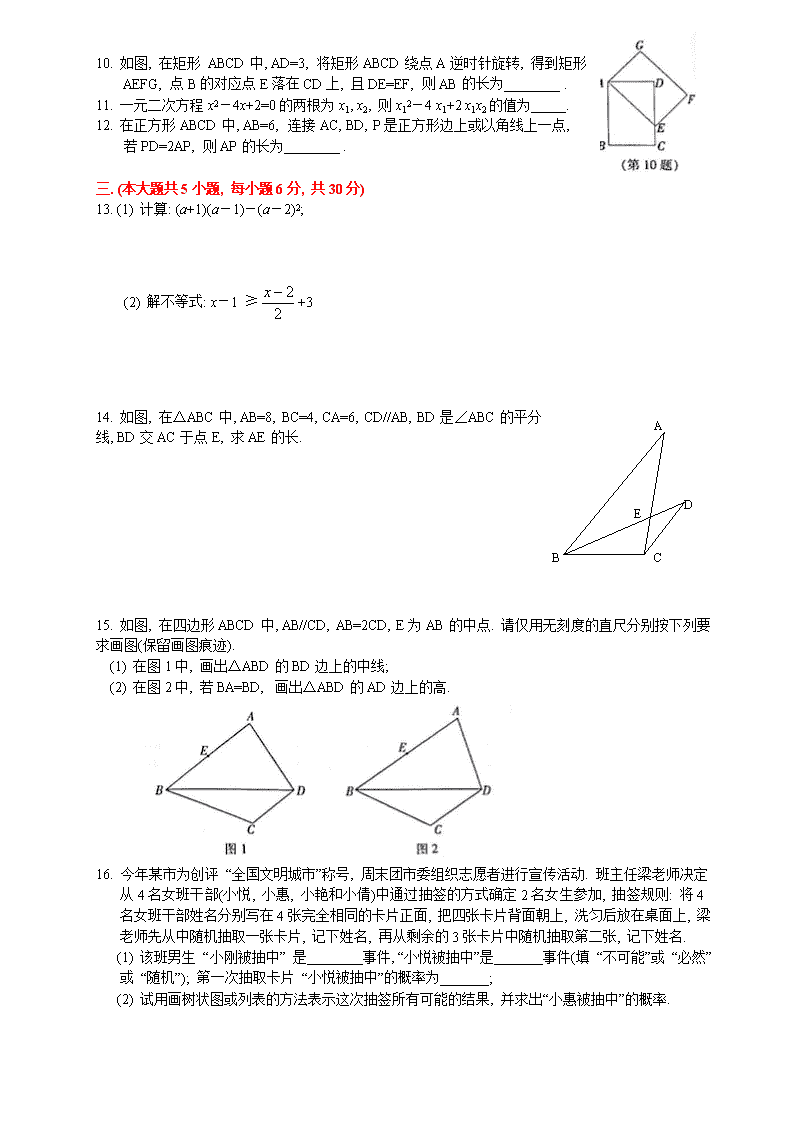10 篮 球 0 项目 频数(人数) 20 25 15 5 12 20 8 64 足 球 羽 毛 球 田 径 乒 乓 球 10. 如图, 在矩形 ABCD 中, AD=3, 将矩形 ABCD 绕点 A 逆时针旋转, 得到矩形 AEFG, 点 B 的对应点 E 落在 CD 上, 且 DE=EF, 则 AB 的长为________ . 11. 一元二次方程 x2－4x+2=0 的两根为 x1, x2, 则 x12－4 x1+2 x1x2 的值为_____. 12. 在正方形 ABCD 中, AB=6, 连接 AC, BD, P 是正方形边上或以角线上一点, 若 PD=2AP, 则 AP 的长为________ . 三. (本大题共 5 小题, 每小题 6 分, 共 30 分) 13. (1) 计算: (a+1)(a－1)－(a－2)2; (2) 解不等式: x－1 ≥ 2 2x +3 14. 如图, 在△ABC 中, AB=8, BC=4, CA=6, CD//AB, BD 是∠ABC 的平分 线, BD 交 AC 于点 E, 求 AE 的长. 15. 如图, 在四边形 ABCD 中, AB//CD, AB=2CD, E 为 AB 的中点. 请仅用无刻度的直尺分别按下列要 求画图(保留画图痕迹). (1) 在图 1 中, 画出△ABD 的 BD 边上的中线; (2) 在图 2 中, 若 BA=BD, 画出△ABD 的 AD 边上的高. 16. 今年某市为创评 “全国文明城市”称号, 周末团市委组织志愿者进行宣传活动. 班主任梁老师决定 从 4 名女班干部(小悦, 小惠, 小艳和小倩)中通过抽签的方式确定 2 名女生参加, 抽签规则: 将 4 名女班干部姓名分别写在4张完全相同的卡片正面, 把四张卡片背面朝上, 洗匀后放在桌面上, 梁 老师先从中随机抽取一张卡片, 记下姓名, 再从剩余的 3 张卡片中随机抽取第二张, 记下姓名. (1) 该班男生 “小刚被抽中” 是________事件, “小悦被抽中”是_______事件(填 “不可能”或 “必 然”或 “随机”); 第一次抽取卡片 “小悦被抽中”的概率为_______; (2) 试用画树状图或列表的方法表示这次抽签所有可能的结果, 并求出“小惠被抽中”的概率. B A D C E 17. 如图, 反比例函数 y= x k (k≠0)的图像与正比例函数 y=2x 的图像相交于 A(1, a), B 两点, 点 C 在第四 象限, CA//y 轴, ∠ABC=90°. (1) 求 k 的值及点 B 的坐标; (2) 求 tanC 的值. 四. (本大题共 3 小题, 每小题 8 分, 共 24 分) 18. 4 月 23 日是世界读书日, 习近平总书记说: “读书可以让人保持思想活力, 让人得到智慧启发, 让人 滋养浩然之气.” 某校响应号召, 鼓励师生利用课余时间广泛阅读. 该校文学社为了解学生课外阅读的 情况, 抽样调查了部分学生每周用于课外阅读的时间, 过程如下: 收集数据 从全校随机抽取 20 名学生, 进行了每周用于课外阅读时间的调查, 数据如下(单位: min): 30 60 81 50 40 110 130 146 90 100 60 81 120 140 70 81 10 20 100 81 整理数据 按如下分段整理样本数据并补全表格: 分析数据 补全下列表格中的统计量: 平均数 中位数 众数 80 得出结论 (1) 用样本中的统计量估计该校学生每周用于课外阅读时间的情况等级为_______; (2) 如果该校现有学生 400 人, 估计等级为 “B”的学生有多少名? (3) 假设平均阅读一本课外书的时间为 160 分钟, 请你选择样本中的一种统计量估计该校学生每人一 年(按 52 周计算)平均阅读多少本课外书? 19. 图 1 是一种折叠门, 由上下轨道和两扇长宽相等的活页门组成, 整 个活页门的右轴固定在门框上, 通过推动左侧活页门开关. 图 2 是其俯 视简化的示意图, 已知轨道 AB=120cm, 两扇活页门的宽 OC=OB=60cm, 点 B 固定, 当点 C 在 AB 上左右运动时, OC 与 OB 的长度不变(所有结果 保留小数点后一位). (1) 若∠OBC=50°,求 AC 的长; (2) 当点 C 从点 A 向右运动 60cm 时, 求点 O 在此过程中运动的路径长. 参考数据: sin50°≈0.77, cos50°≈0.64, tan50°≈1.19, π取 3.14 课外阅读时间 x(min) 0≤ x <40 40≤ x <80 80≤ x <120 120≤ x <160 等级 D C B A 人数 3 8 20. 如图, 在△ABC 中, O 为 AC 上一点, 以点 O 为圆心, OC 为半径作圆, 与 BC 相切于点 C, 过点 A 作 AD⊥BO 交 BO 的延长线于点 D, 且∠AOD=∠BAD. (1) 求证: AB 为⊙O 的切线; (2) 若 BC=6, tan∠ABC= 3 4 , 求 AD 的长. 五. (本大题共 2 小题, 每小题 9 分, 共 18 分) 21. 某乡镇实施产业扶贫, 帮助贫困户承包了荒山种植某品种蜜柚, 到了收获季节, 已知该蜜柚的成 本价为 8 元/千克, 投入市场销售时, 调查市场行情, 发现该蜜柚销售不会亏本, 且每天销售量 y(千克) 与销售单位 x(元/千克)之间的函数关系如图所示. (1) 求 y 与 x 的函数关系式, 并写出 x 的取值范围; (2) 当该品种蜜柚定价为多少时, 每天销售获得的利润最大? 最大利润 是多少? (3) 某农户今年共采摘蜜柚 4800 千克, 该品种蜜柚的保质期为 40 天, 根 据(2)中获得最大利润的方式销售, 能否销售完这批蜜柚?请说明理由. 22. 在菱形 ABCD 中, ∠ABC=60°, 点 P 是射线 BD 上一动点, 以 AP 为边向右侧作等边△APE. 点 E 的位置随着点 P 的位置变化而变化. (1) 如图 1, 当点 E 在菱形 ABCD 内部或边上时, 连接 CE, BP 与 CE 的数量关系是_________. CE 与 AD 的位置关系是________; (2) 当点 E 在菱形 ABCD 外部时, (1)中的结论是否成立? 若成立, 请予以证明; 若不成立, 请说明理由 (选择图 2,图 3 中的一种情况予以证明或说理). (3) 如图 4, 当点 P 在线段 BD 的延长线上时, 连接 BE, 若 AB= 32 , BE= 192 , 求四边形 ADPE 的 面积. 图 1 图 2 图 3 图 4 六. (本大题共 12 分) 23. 小贤与小杰在探究某类二次函数问题时, 经历了如下过程: 求解体验 (1) 已知抛物线 y=－x2+bx－3 经过点(－1, 0), 则 b=______, 顶点坐标为__________, 该抛物线关于 点(0, 1)成中心对称的抛物线表达式是__________________ . 抽象感悟 我们定义:对于抛物线 y=ax2+bx+c(a≠0), 以 y 轴上的点 M(0, m)为中心, 作该抛物线关于点 M 的对称抛 物线 y’, 则我们又称抛物线 y’为抛物线线 y 的 “衍生抛物线”, 点 M 为 “衍生中心” . (2) 已知抛物线 y=－x2－2x+5 关于点(0, m)的衍生抛物线 y’. 若这两抛物线有交点, 求 m 的取值范围. 问题解决 (3) 已知抛物线 y=ax2+2ax－b(a≠0), ① 若抛物线 y 的衍生抛物线 y’= bx2－2bx+a2(b≠0). 两抛物线有两个交点, 且恰好是它们的顶点, 求 a, b 的值及衍生中心的坐标; ② 若抛物线 y 关于点(0, k+12)的衍生抛物线为 y1, 其顶点为 A1; 关于点(0, k+22) )的衍生抛物线为 y2, 其顶点为 A2; … ; 关于点(0, k+n2) )的衍生抛物线为 yn, 其顶点为 An; … ; (n 为正整数) 求 AnAn+1 的长(用含 n 的式子表示). 参考答案: 一. 选择题 1 2 3 4 5 6 B A D D C D 二. 填空题 备用图片: