中考数学 选择题解法举例复习 17页

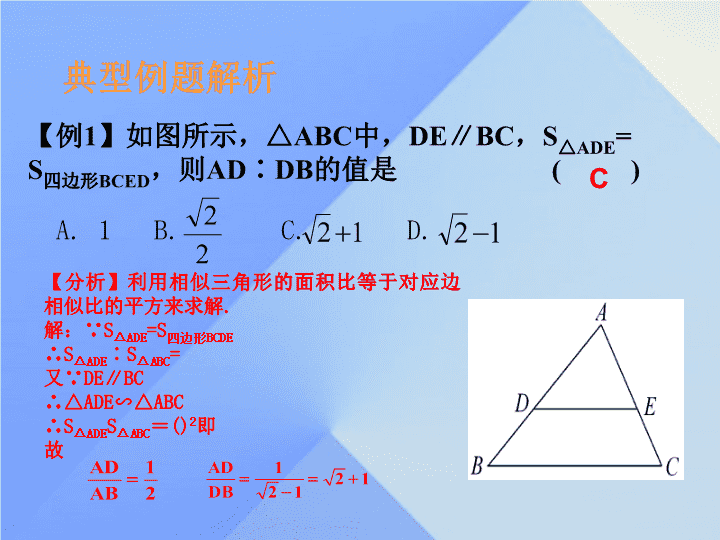
选择题解法举例 选择题历年都是中考的必考题型，主要考查对基 本知识和基本技能的掌握情况，但方法越来越灵活， 常见的方法有：直接计算法、代入检验法、概念辨别 法、特殊值法、筛选法等等，同时还可能兼顾到学科 交叉、推理探索等题型 . 解选择题的关键在于能熟练运 用各种解题方法或手段，以提高解题的效率和正确率 . 典型例题解析 【 例 1 】 如图所示，△ ABC 中， DE ∥ BC ， S △ ADE = S 四边形 BCED ，则 AD ∶ DB 的值是 ( ) A. 1 B. C. D. 【 分析 】 利用相似三角形的面积比等于对应边相似比的平方来求解 . 解：∵ S △ADE =S 四边形 BCDE ∴S △ADE ∶S △ABC = 又∵ DE∥BC ∴△ADE∽△ABC ∴S △ADE S △ABC ＝ () 2 即 故 C 【 例 2】 将进货单价为 70 元的某种商品按零售价 100 元一个出售时，每天能卖出 20 个，若这种商品的零售价在一定范围内每降价 1 元，其日销量就增加 1 个，为了获得最大利润，则应降价 ( ) A.5 元 B.10 元 C.15 元 D.20 元 【 解析 】 利用二次函数最值求解的方法即可求得结果 . 解：设每个商品降价 x 元，则销售量增加 x 个 . 故，所求利润 y=(100-x)(20+x)-70(20+x) =-x 2 +10x+600 =-(x-5) 2 +625 ∴ 当 x=5 时， y 取最大值 . ∴ 本题选 A. 【 点评 】 本题是从已知条件出发，进行运算或推理，求得正确的结论，从而作出正确的选择，这种解法叫做直接法，这是解选择题的常用基本方法，应用广泛，应熟练掌握 . A 【 例 3】 若 m 为实数，方程 x 2 -3x+m=0 的根的相反数是方程 x 2 +3x-m=0 的根，那么方程 x 王 2-3x+m=0 的根是 ( ) A.x 1 =-1 ， x 2 =-2 B.x 1 =1 ， x 2 =2 C.x 1 =0 ， x 2 =3 D.x 1 = ， x 2 =   【 分析 】 只要将 A 、 B 、 C 、 D 四个选项逐一代入求解验证即可 . 解：若 x 1 =-1 ， x 2 =-2 ，则 m=2 ，经检验， -x ， -x 2 均不是方程 x 2 +3x-m=0 的根； 若 x 1 =1 ， x 2 =2 ，则 m=2 ，经检验， -x ， -x 2 也都不是方程 x 2 +3x-m=0 的根； 若 x 1 =0 ， x 2 =3 ，则 m=0 ，经检验， -x ， -x 2 都是方程 x 王 2+3x-m=0 的根 . ∵A 、 B 、 C 、 D 中有且仅有一个答案正确 . ∴ 本题选 C. C 【 例 4】 方程 7x-3+x-1=2 的解集是 ( ) A.x=3 B.x= C.x=2 D.x= 1 【 分析 】 将每个选项依次代入验证即可 . 解：当 x=3 时左边 = ≠2 当 x= 时左边 = ≠2 当 x=2 时左边 = ≠2 当 x=1 时左边 = =2 ∴ 本题选 D. D 【 点评 】 以上 3 ， 4 题都是把各个选择支代入原题加以验证，以决定取舍，选择题的这种解法叫做代入检验法或代入法 . 【 例 5】 下列命题： (1) 相等的圆心角所对的弦的弦心距也相等； (2) 相交两圆的交点关于连心线对称； (3) 圆内接四边形的一个外角等于它的内对角； (4) 与已知直线 l 相切且半径等于 r 的圆的圆心的轨迹是平行于直线 l 且到 l 的距离等于 r 的一条直线，其中假命题有 ( ) 个 . A.4 B.3 C.2 D.1 【 分析 】 命题 (1) 应增加限制条件：在同圆或等圆中；由于连心线是两圆的对称轴，故命题 (2) 正确；命题 (3) 是课本中的定理，当然正确；但对命题 (4) ，根据基本轨迹，满足条件的圆心的轨迹应是二条平行线，故命题 (4) 是假命题，从而假命题共 2 个 . 【 点评 】 ：这是一组概念辨别题，根据定理、推论及相关基础知识、基本性质从而辨别命题的真伪方法叫做概念辨别法 . C 【 例 6】 当 0 ＜ a ＜ b ＜ 1 时，下列各式成立的是 ( ) A. ＞ - B. ＜ C. ＜ - D.-b ＞ -a 【 分析 】 选择符合条件 0 ＜ a ＜ b ＜ 1 的特殊值，如 a= ， b= ，依次代入选择支 A 、 B 、 C 、 D.C 满足 . C 【 例 7】 当 0° ＜ α ＜ 45° 时，下列各式成立的是 ( ) A.cosα ＜ sinα ＜ tanα B.sinα ＜ cosα ＜ cotα C.sinα ＜ cotα ＜ cosα D.cotα ＜ sinα ＜ cosα 【 分析 】 选择符合条件 0° ＜ α ＜ 45° 的特殊值 α ＝ 30° 则 sin α= ； cos α ＝ ； tan α ＝ ； cot α= ，依次代入选项 A 、 B 、 C 、 D 中，只有 B 满足 . B 【 例 8】 化简 -a · 3a 的结果是 ( ) A. B. C.- D.- D 【 分析 】 由本题条件可知， a ＜ 0 ， · ＜ 0 ，考察 A 显然与根式乘法矛盾；而 B 中 ＞ 0 ， (C) 中 - 无意义，均应排除，因为 A 、 B 、 C 、 D 中有且仅有一支正确 . 【 例 9】 以一元二次方程 x 2 -3x-10=0 的两根倒数为根的方程是 ( ) A.10x 2 +3x+1=0 B.10x 2 +3x-1=0 C.10x 2 -3x+1=0 D.10x 2 -3x-1=0 【 分析 】 由根与系数的关系知，新方程二根应异号，且正根的绝对值较小，逐一排除 A 、 C 、 D 解：本题选 B. 【 点评 】 第 8 、 9 两题通过对各个选择支的考察，逐一排除错误选择支，以便确定正确的答案，选择题的这种解法叫做排除法或筛选法 . B 【 例 10】 如图完成 L 照射到平面镜 I ， II 之间来回反射，已知∠ α ＝ 55° ，∠ γ ＝ 75° ，则∠ β=( ) A.50° B.55° C.60 ° D.65 ° 【 分析 】 本题是应用数学知识解决物理中光学问题，体现学科交叉思想， 由入射角等于反射角知：∠ 1=∠α=55° ，∠ 2=∠γ=75° ，于是∠ 4=180°-(∠1+∠2)=50° ，所以∠ β=∠3=12(180°-∠4)=65° D 1. 已知∠ A 为锐角，且 cos A≤ ，那么 ( ) A.0° ＜ A≤60° B.60°≤A ＜ 90° C.0° ＜ A≤30° D.30°≤A ＜ 90° 解：因为 cos 60°=12 且余弦函数随着 角度的增大三角函数值反而减小，故选择 B. B 2. 已知 a ＜ b ＜ 0 ，那么下列各式中成立的是 ( ) A.a 2 ＜ b 2 B. ＜ 1 C.a ＜ 4-b D. ＜ 解：利用特殊值检验法，因为 a ＜ b ＜ 0 ，为方便计算，可取 a=-2 ， b=-1 ，经验证，容易得到 a ＜ 4-b ，即选择 C. C 3. 设二次方程 x 2 +2px+2q=0 有实数根，其中 p 、 q 都是奇数，那么它的根是 ( ) A. 奇数 B. 偶数 C. 分数 D. 无理数 解：选择满足 “ 奇数 ” 条件的特殊值： p=3 ， q=1 代入所给方程中，可解得方程的根为 x=-3±7 ，显然这是个无理数，故选择 D. D 4. 使二次方程 2kx 2 +(8k+1)x+8k=0 有两个不相等的实数根的 k 的取值范围是 ( ) A.k ＜ - B.k ＞ - C.k≥- D. 不同于 A 、 B 、 C 的答案 D 解：此题可用筛选法缩小讨论的范围，因为方程是一元二次方程，所以二次项的系数 2k≠0 ，但在 “ B ” 和 “ C ” 中均含有 k=0 ，所以应予以排除，而考虑 “ A ” 和 “ D ” ，我们取 k=- ( ＜ - ) 代入方程中，有 - x 2 -1=0 ，容易看出，该方程无实数根，故 “ A ” 也不对，仅能选 “ D ” . 5. 若代数式 2x 2 +3x+7 的值为 8 ，则代数式 4x 2 +6x-9 的值是 ( ) A.2 B.-17 C.-7 D.7 解：本题应用求代数式的值的一个重要方法 —— 整体代入法 . 观察系数 2 ， 3 及 4 ， 6 ，它们对应成比例，故可将 2x 2 +3x 看成一个整体，求出 2x 2 +3x=1 代入 4x 2 +6x-9 中得到 2(2x 2 +3x)-9=2 × 1-9=-7 故应选择 C C 6. 如图 Z1-3 ，以正三角形的三边为弦作弧交于△ ABC 的外心 O ，则所得的菊形的面积为 ( ) A. 两个三角形的面积减去三个方形面积 B. 一个三角形的面积减去三个弓形的面积 C. 三个弓形的面积减去一个三角形的面积 D. 三个弓形的面积减去两个三角形的面积 解：运用构造法及面积割补法是解决此类题目行之有效的方法 . 设正三角形内的非阴影部分的面积为 3x ，阴影部分的面积为 3y ，则： 3x+3y=S △ x+2y=S 弓 故得 3y=3S 弓 -S △ 故选 C. 图 Z1-3 C 2017 年中考 取得成功