2015年黄冈市中考数学试题及答案] 7页

初中毕业生学业水平考试数学试题 第Ⅰ卷（选择题共21 分）‎ 一、选择题（下列各题的备选答案中，有且仅有一个答案是正确的，每小题3 分，共21 分）‎ ‎1.9 的平方根是( )‎ A.±3 B.± C.3 D.-3‎ ‎2.下列运算结果正确的是( )‎ A.x6÷x2=x3 B.(-x)-1= C. (2x3)2=4x6 D.-2a2·a3=-2a6‎ ‎3.如图所示，该几何体的俯视图是( )‎ ‎4.下列结论正确的是( )‎ A.3a2b-a2b=2‎ B.单项式-x2的系数是-1‎ C.使式子有意义的x 的取值范围是x>-2‎ D.若分式的值等于0,则a=±1‎ ‎5.如图，a∥b,∠1=∠2,∠3=40°,则∠4 等于( )‎ A.40° B.50° C.60° D.70°‎ ‎6.如图，在△ABC 中，∠C=Rt∠，∠B=30°，边AB 的垂直平分线DE 交AB 于点E，交BC 于点D，CD=3，则BC 的长为( )‎ A.6 B. C.9 D. ‎ ‎7.货车和小汽车同时从甲地出发,以各自的速度匀速向乙地行驶,小汽车到达乙地后,立即以相同的速度沿原路返回甲地.已知甲、乙两地相距180 千米，货车的速度为60 千米/小时,小汽车的速度为90 千米/小时,则下图中能分别反映出货车、小汽车离乙地的距离y(千米)与各自行驶时间t(小时)之间的函数图象是( )‎ 第Ⅱ卷（非选择题共99 分）‎ 二、填空题（共7 小题，每小题3 分,共21 分）‎ ‎8.计算：=_______________‎ ‎9.分解因式：x3-2x2+x=____________‎ ‎10.若方程x2-2x-1=0 的两根分别为x1，x2，则x1+x2-x1x2 的值为_________________.‎ ‎11.计算的结果是_____________.‎ ‎12.如图，在正方形ABCD 中，点F 为CD 上一点,BF 与AC交于点E,若∠CBF=20°，则∠AED 等于_____________度.‎ ‎13. 如图所示的扇形是一个圆锥的侧面展开图, 若∠AOB=120° , 弧AB 的长为12πcm, 则该圆锥的侧面积为_______cm2.‎ ‎14. 在△ ABC 中,AB=13cm,AC=20cm,BC 边上的高为12cm,则△ABC 的面积为__________cm2.‎ 三、解答题（本大题共10 小题，满分共78 分）‎ ‎15.（5分）解不等式组：‎ ‎16.（6分）已知A,B两件服装的成本共500元，鑫洋服装店老板分别以30%和20%的利润率定价后进行销售，该服装店共获利130 元，问A,B 两件服装的成本各是多少元？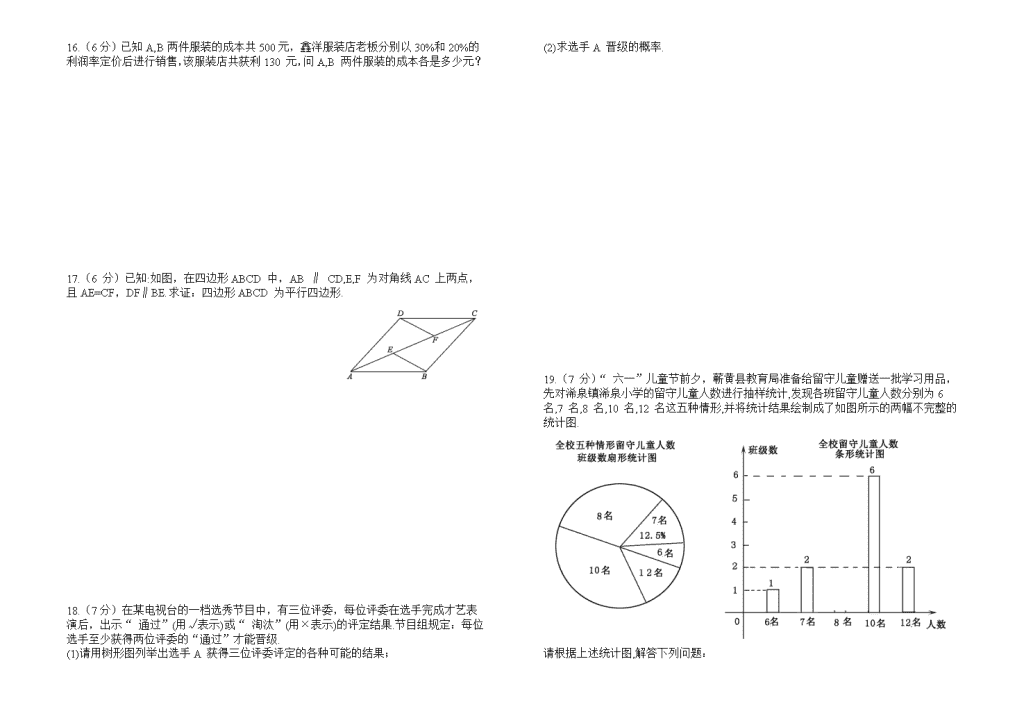‎ ‎17.（6 分）已知:如图，在四边形ABCD 中，AB ∥ CD,E,F 为对角线AC 上两点，且AE=CF，DF∥BE.求证：四边形ABCD 为平行四边形.‎ ‎18.（7分）在某电视台的一档选秀节目中，有三位评委，每位评委在选手完成才艺表演后，出示“ 通过”(用√表示)或“ 淘汰”(用×表示)的评定结果.节目组规定：每位选手至少获得两位评委的“通过”才能晋级.‎ ‎(1)请用树形图列举出选手A 获得三位评委评定的各种可能的结果；‎ ‎(2)求选手A 晋级的概率.‎ ‎19.（7 分）“ 六一”儿童节前夕，蕲黄县教育局准备给留守儿童赠送一批学习用品，先对浠泉镇浠泉小学的留守儿童人数进行抽样统计,发现各班留守儿童人数分别为6 名,7 名,8 名,10 名,12 名这五种情形,并将统计结果绘制成了如图所示的两幅不完整的统计图. ‎ 请根据上述统计图,解答下列问题：‎ ‎(1)该校有多少个班级?并补全条形统计图;‎ ‎(2)该校平均每班有多少名留守儿童?留守儿童人数的众数是多少？‎ ‎(3)若该镇所有小学共有60 个教学班,请根据样本数据,估计该镇小学生中,共有多少名留守儿童.‎ ‎20.(7 分)如图,在一次军事演习中,蓝方在一条东西走向的公路上的A 处朝正南方向撤退,红方在公路上的B 处沿南偏西60°方向前进实施拦截.红方行驶1000 米到达C 处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D 处成功拦截蓝方.求拦截点D 处到公路的距离(结果不取近似值). ‎ ‎21.（ 8分）已知：如图，在△ABC中，AB=AC，以AC为直径的⊙O 交AB 于点M，交BC 于点N，连接AN,过点C 的切线交AB 的延长线于点P.‎ ‎（1）求证：∠BCP=∠BAN;‎ ‎（2）求证：‎ ‎22.（8 分）如图，反比例函数y=的图象经过点A（-1,4),直线y=-x + b(b≠0) 与双曲线y=在第二、四象限分别相交于P，Q 两点，与x 轴、y 轴分别相交于C,D 两点.‎ ‎(1)求k 的值;‎ ‎(2)当b=-2 时，求△OCD 的面积；‎ ‎(3)连接OQ，是否存在实数b,使得S△ODQ=S△OCD？ 若存在，请求出b 的值；若不存在，请说明理由. ‎ ‎23.（10 ‎ 分）我市某风景区门票价格如图所示黄冈赤壁旅游公司有甲、乙两个旅行团队,计划在“五一”小黄金周期间到该景点游玩，两团队游客人数之和为120 人，乙团队人数不超过50 人.设甲团队人数为x 人,如果甲、乙两团队分别购买门票,两团队门票款之和为W 元.‎ ‎(1)求W 关于x 的函数关系式，并写出自变量x 的取值范围；‎ ‎(2)若甲团队人数不超过100 人，请说明甲、乙两团队联合购票比分别购票最多可节约多少钱；‎ ‎(3“) 五一”小黄金周之后，该风景区对门票价格作了如下调整：人数不超过50 人时，门票价格不变；人数超过50 人但不超过100 人时，每张门票降价a 元;人数超过100 人时，每张门票降价2a 元.在（2）的条件下，若甲、乙两个旅行团队“五一”小黄金周之后去游玩，最多可节约3400 元，求a 的值.‎ ‎24.（14 分）如图，在矩形OABC 中，OA=5，AB=4，点D 为边AB 上一点,将△BCD 沿直线CD 折叠,使点B 恰好落在OA边上的点E 处，分别以OC，OA 所在的直线为x 轴，y 轴建立平面直角坐标系.‎ ‎(1)求OE 的长；‎ ‎(2)求经过O，D，C 三点的抛物线的解析式；‎ ‎(3)一动点P 从点C 出发，沿CB 以每秒2 个单位长的速度向点B 运动，同时动点Q 从E 点出发，沿EC 以每秒1 个单位长的速度向点C 运动，当点P 到达点B 时，两点同时停止运动.设运动时间为t 秒，当t为何值时，DP=DQ；‎ ‎(4) 若点N 在(2)中的抛物线的对称轴上，点M 在抛物线上,是否存在这样的点M与点N，使得以M，N，C，E 为顶点的四边形是平行四边形？若存在，请求出M 点的坐标;若不存在，请说明理由.‎